Tìm tọa độ của 0→.

Câu hỏi:

Tìm tọa độ của $\overrightarrow{0}$.

Trả lời:

Ta có: $\overrightarrow{0}=0.\overrightarrow{i}+0.\overrightarrow{j}\Rightarrow \overrightarrow{0}\left(0;0\right)$.
Vậy tọa độ của $\overrightarrow{0}$ là $\overrightarrow{0}\left(0;0\right).$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

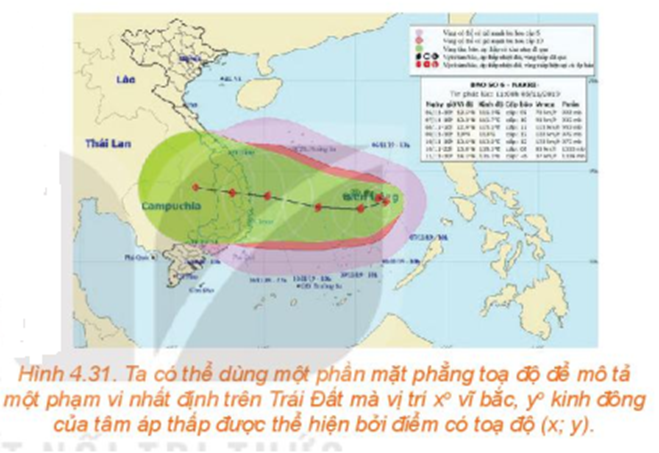
1. Một bản tin dự báo thời tiết thể hiện đường đi trong 12 giờ của một cơn bão trên một mặt phẳng tọa độ. ,Trong thời gian đó, tâm bão di chuyển thẳng đều từ vị trí có tọa độ (13,8; 108,3) đến vị trí tọa độ (14,1; 106,3). Dựa vào thông tin trên, liệu ta có thể dự đoán được vị trí của tâm bão tại thời điểm bất kì trong khoảng thời gian 12 giờ đó hay không?
   
   

   Câu hỏi:
   

   Một bản tin dự báo thời tiết thể hiện đường đi trong 12 giờ của một cơn bão trên một mặt phẳng tọa độ. ,Trong thời gian đó, tâm bão di chuyển thẳng đều từ vị trí có tọa độ (13,8; 108,3) đến vị trí tọa độ (14,1; 106,3). Dựa vào thông tin trên, liệu ta có thể dự đoán được vị trí của tâm bão tại thời điểm bất kì trong khoảng thời gian 12 giờ đó hay không?
   

   Trả lời:

   Sau bài học này ta có thể trả lời câu hỏi này như sau:
   Dựa vào thông tin trên, ta có thể dự đoán được tâm bão tại thời điểm bất kì trong khoảng thời gian 12 giờ đó.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

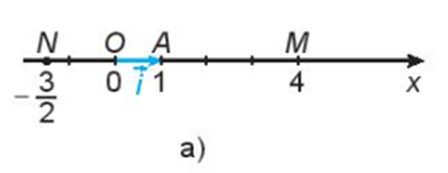
2. Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt OA→=i→ (H.4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số −32. Hãy biểu thị mỗi vecto OM→,ON→ theo vecto đơn vị i→.
   
   

   Câu hỏi:
   

   Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt $\overrightarrow{OA}=\overrightarrow{i}$ (H.4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số $-\frac{3}{2}.$ Hãy biểu thị mỗi vecto $\overrightarrow{OM},\overrightarrow{ON}$ theo vecto đơn vị $\overrightarrow{i}$.

   

   Trả lời:

   Ta có vecto $\overrightarrow{OM}$ cùng hướng với vecto $\overrightarrow{OA}$ và OM = 4OA nên ta có $\overrightarrow{OM}=4\overrightarrow{OA}=4\overrightarrow{i}$.
   Ta có vecto $\overrightarrow{ON}$ ngược hướng với vecto $\overrightarrow{OA}$ và ON = $\frac{3}{2}$OA nên ta có $\overrightarrow{ON}=-\frac{3}{2}\overrightarrow{OA}=-\frac{3}{2}\overrightarrow{i}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

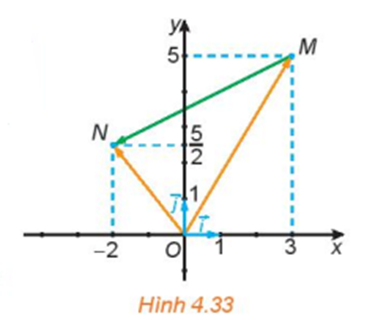
3. Trong Hình 4.33: a) Hãy biểu thị mỗi vecto OM→,ON→ theo các vecto i→,j→. b) Hãy biểu thị vecto MN→ theo các vecto OM→,ON→ từ đó biểu thị vecto MN→ theo các vecto i→,j→.
   
   

   Câu hỏi:
   

   Trong Hình 4.33:
   a) Hãy biểu thị mỗi vecto $\overrightarrow{OM},\overrightarrow{ON}$ theo các vecto $\overrightarrow{i},\overrightarrow{j}$.
   b) Hãy biểu thị vecto $\overrightarrow{MN}$ theo các vecto $\overrightarrow{OM},\overrightarrow{ON}$ từ đó biểu thị vecto $\overrightarrow{MN}$ theo các vecto $\overrightarrow{i},\overrightarrow{j}$.
   

   Trả lời:

   

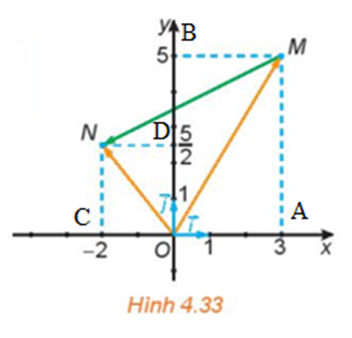
   a) Xét hình bình hành OAMB, có:
   $\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{OB}=3\overrightarrow{i}+5\overrightarrow{j}$ (quy tắc hình bình hành)
   Xét hình bình hành OCND, có:
   $\overrightarrow{ON}=\overrightarrow{OC}+\overrightarrow{OD}=-2\overrightarrow{i}+\frac{5}{2}\overrightarrow{j}$ (quy tắc hình bình hành)
   b) Xét tam giác OMN, có:
   $\overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM}$ (quy tắc ba điểm)
   $\overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM}=-2\overrightarrow{i}+\frac{5}{2}\overrightarrow{j}-\left(3\overrightarrow{i}+5\overrightarrow{j}\right)=-5\overrightarrow{i}-\frac{5}{2}\overrightarrow{j}.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

4. Trong mặt phẳng tọa độ Oxy, cho u→=2;−3,v→=4;1,a→=8;−12. a) Hãy biểu thị mỗi vecto u→,v→,a→ theo các vecto i→,j→. b) Tìm tọa độ của các vecto u→+v→,4u→. c) Tìm mối liên hệ giữa hai vecto u→,a→.
   
   

   Câu hỏi:
   

   Trong mặt phẳng tọa độ Oxy, cho $\overrightarrow{u}=\left(2;-3\right),\overrightarrow{v}=\left(4;1\right),\overrightarrow{a}=\left(8;-12\right).$
   a) Hãy biểu thị mỗi vecto $\overrightarrow{u},\overrightarrow{v},\overrightarrow{a}$ theo các vecto $\overrightarrow{i},\overrightarrow{j}.$
   b) Tìm tọa độ của các vecto $\overrightarrow{u}+\overrightarrow{v},4\overrightarrow{u}.$
   c) Tìm mối liên hệ giữa hai vecto $\overrightarrow{u},\overrightarrow{a}.$

   Trả lời:

   a) Ta có:
   
   b) Ta có:
   
   c) Ta có $\overrightarrow{a}=\left(8;-12\right)=4\overrightarrow{u}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

5. Trong mặt phẳng toạ độ Oxy, cho điểm M(x0;y0) . Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy (H.4.35). a) Trên trục Ox, điểm P biểu diễn số nào? Biểu thị OP→ theo i→ và tính độ dài của OP→ theo x0. b) Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị OQ→ theo j→ và tính độ dài của OP→ theo y0. c) Dựa vào hình chữ nhật OPMQ, tính độ dài của OM→ theo x0, y0. d) Biểu thị OM→ theo các vecto i→,j→.    
   
   

   Câu hỏi:
   

   Trong mặt phẳng toạ độ Oxy, cho điểm M(x₀;y₀) . Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy (H.4.35).
   a) Trên trục Ox, điểm P biểu diễn số nào? Biểu thị $\overrightarrow{OP}$ theo $\overrightarrow{i}$ và tính độ dài của $\overrightarrow{OP}$ theo x₀.
   b) Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị $\overrightarrow{OQ}$ theo $\overrightarrow{j}$ và tính độ dài của $\overrightarrow{OP}$ theo y₀.
   c) Dựa vào hình chữ nhật OPMQ, tính độ dài của $\overrightarrow{OM}$ theo x₀, y₀.
   d) Biểu thị $\overrightarrow{OM}$ theo các vecto 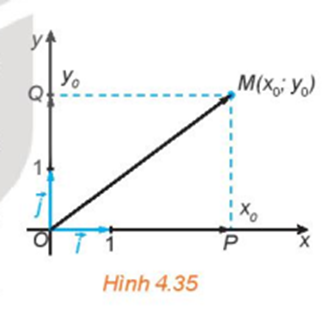$\overrightarrow{i},\overrightarrow{j}$.    

   

   Trả lời:

   a) Trên trục Ox, điểm P biểu diễn cho số x₀;
   Độ dài đoạn thẳng OP = |x₀| = x₀.
   Ta có vecto $\overrightarrow{OP}$ cùng hướng với vecto và OP = x₀ nên $\overrightarrow{OP}=x_0\overrightarrow{i}.$
   b) Trên trục Oy, điểm Q biểu diễn cho số y₀;
   Độ dài đoạn thẳng OQ = |y₀| = y₀.
   Ta có vecto $\overrightarrow{OQ}$ cùng hướng với vecto $\overrightarrow{j}$ và OQ = y₀ nên $\overrightarrow{OQ}=y_0\overrightarrow{j}.$
   c) Xét tam giác OPM vuông tại P, có:
   $OM=\sqrt{O{P}^2+M{P}^2}=\sqrt{O{P}^2+O{Q}^2}=\sqrt{x_0^2+y_0^2}.$
   Vậy $\left|\overrightarrow{OM}\right|=\sqrt{x_0^2+y_0^2}.$
   d) Ta có $\overrightarrow{OM}=\overrightarrow{OP}+\overrightarrow{OQ}=x_0\overrightarrow{i}+y_0\overrightarrow{j}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====