Lý thuyết Hai mặt phẳng song song (Chân trời sáng tạo 2023) hay, chi tiết

Lý thuyết Toán lớp 11 Bài 4: Hai mặt phẳng song song
A. Lý thuyết Hai mặt phẳng song song
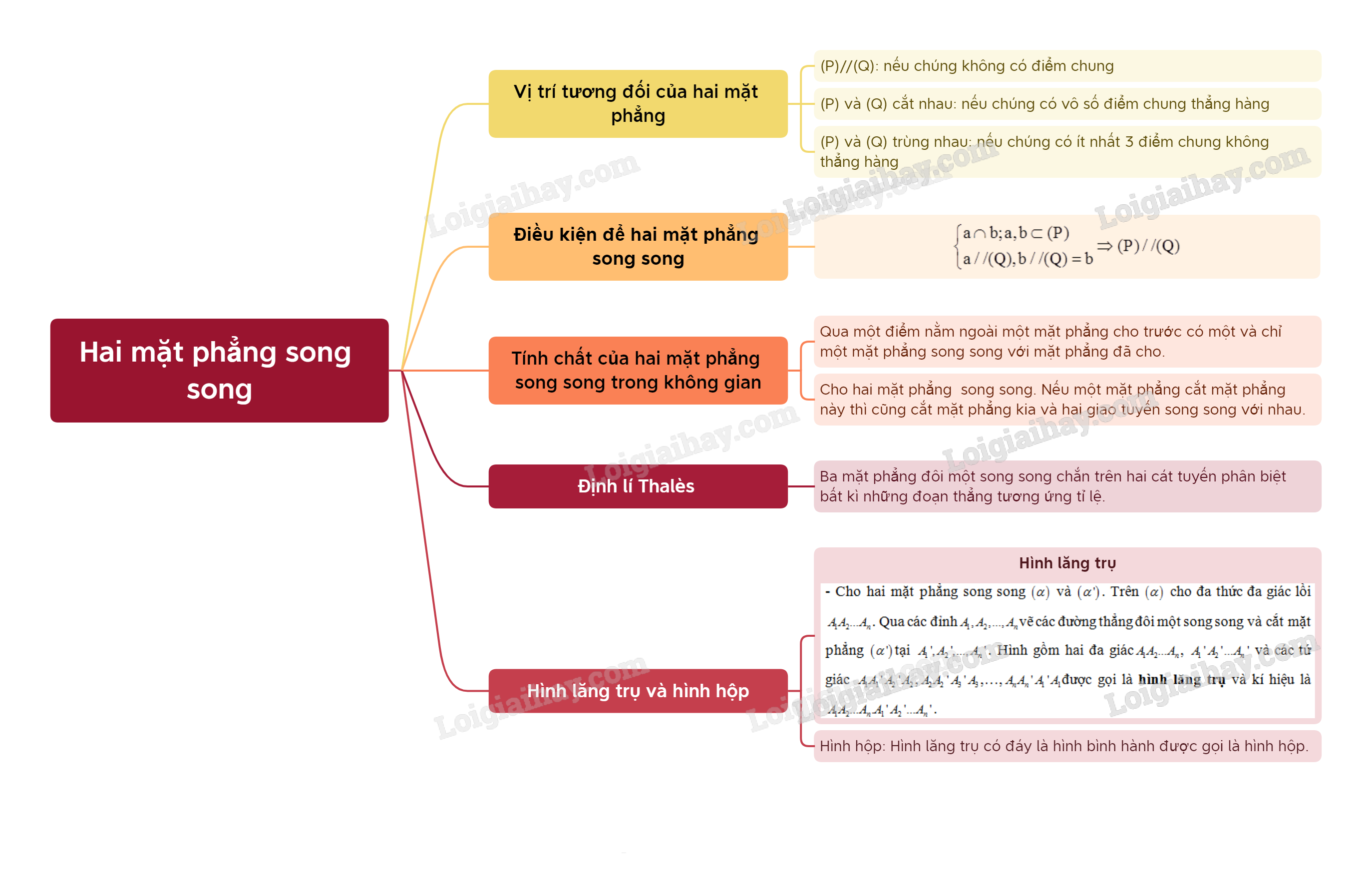
1. Hai mặt phẳng song song
Nếu $(P)$ và $(Q)$ có 3 điểm chung không thẳng hàng, thì (P) trùng (Q), kí hiệu $(P) \equiv (Q)$ .
(ảnh 1)
Nếu $(P)$ và $(Q)$ phân biệt và có một điểm chung thì (P) và (Q) cắt nhau theo giao tuyến d đi qua điểm chung, kí hiệu $(P) \cap (Q) = d$ .
(ảnh 2)
Nếu $(P)$ và $(Q)$ không có bất kì điểm chung nào, thì (P) và (Q) song song với nhau, kí hiệu $(P)$ // $(Q)$ hay $(Q)$ // $(P)$ .
(ảnh 3)
Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm chung.
2. Điều kiện để hai mặt phẳng song song
Nếu mặt phẳng $(P)$ chứa hai đường thẳng cắt nhau a,b và a,b cùng song song với mặt phẳng phẳng $(Q)$ thì $(P)$ song song với $(Q)$
(ảnh 4)
3. Tính chất của hai mặt phẳng song song
Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
(ảnh 5)
Cho hai mặt phẳng $(P)$ và $(Q)$ song song. Nếu mặt phẳng $(R)$ cắt mặt phẳng $(P)$ thì cũng cắt mặt phẳng $(Q)$ và hai giao tuyến song song với nhau.
(ảnh 6)
4. Định lí Thalès trong không gian
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.
(ảnh 7)
$\frac{A B}{A^{'} B^{'}} = \frac{B C}{B^{'} C^{'}} = \frac{A C}{A^{'} C^{'}}$
5. Hình lăng trụ và hình hộp
– Cho hai mặt phẳng song song $(P)$ và $(P^{'})$ . Trên $(P)$ cho đa thức đa giác lồi $A_{1} A_{2} . . . A_{n}$ . Qua các đỉnh $A_{1}, A_{2}, . . ., A_{n}$ vẽ các đường thẳng đôi một song song và cắt mặt phẳng $(P^{'})$ tại ${A_{1}}^{'}, {A_{2}}^{'}, . . ., {A_{n}}^{'}$ . Hình gồm hai đa giác $A_{1} A_{2} . . . A_{n}$ , ${A_{1}}^{'} {A_{2}}^{'} . . . {A_{n}}^{'}$ và các tứ giác $A_{1} {A_{1}}^{'} {A_{2}}^{'} A_{2}$ , $A_{2} {A_{2}}^{'} {A_{3}}^{'} A_{3}$ ,…, $A_{n} {A_{n}}^{'} {A_{1}}^{'} A_{1}$ được gọi là hình lăng trụ và kí hiệu là $A_{1} A_{2} . . . A_{n} . {A_{1}}^{'} {A_{2}}^{'} . . . {A_{n}}^{'}$ .

– Các điểm $A_{1}, A_{2}, . . ., A_{n}$ và ${A_{1}}^{'}, {A_{2}}^{'}, . . ., {A_{n}}^{'}$ được gọi là các đỉnh, các đoạn thẳng $A_{1} {A_{1}}^{'}, A_{2} {A_{2}}^{'}, . . ., A_{n} {A_{n}}^{'}$ được gọi là các cạnh bên, các đoạn thẳng $A_{1} A_{2}, A_{2} A_{3}, . . ., A_{n} A_{1}$ và ${A_{1}}^{'} {A_{2}}^{'}, {A_{2}}^{'} {A_{3}}^{'}, . . ., {A_{n}}^{'} {A_{1}}^{'}$ gọi là cạnh đáy của hình trụ.
– Hai đa giác $A_{1} A_{2} . . . A_{n}$ và ${A_{1}}^{'} {A_{2}}^{'} . . . {A_{n}}^{'}$ được gọi là hai mặt đáy của hình lăng trụ.
Các tứ giác $A_{1} {A_{1}}^{'} {A_{2}}^{'} A_{2}$ , $A_{2} {A_{2}}^{'} {A_{3}}^{'} A_{3}$ ,…, $A_{n} {A_{n}}^{'} {A_{1}}^{'} A_{1}$ gọi là các mặt bên của hình trụ.
(ảnh 8)
– Hình lăng trụ có đáy là tam giác, tứ giác, ngũ giác,…tương ứng được gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác,…
(ảnh 9)
– Hình hộp là hình lăng trụ có đáy là hình bình hành.
(ảnh 10)
– Trong hình hình hộp có:
+ Sáu mặt là sau hình bình hành. Mỗi mặt đều có một mặt song song với nó gọi là hai mặt đối diện.
+ Hai đỉnh không cùng nằm trưn một mặt gọi là hai đỉnh đối diện.
+ Đoạn thẳng nối 2 đỉnh đối diện gọi là đường chéo.
+ Bốn đường chéo cắt nhau tại trung điểm mỗi đường.

B. Bài tập Hai mặt phẳng song song
Đang cập nhật …
Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Chương 1: Hàm số lượng giác và phương trình lượng giác
Lý thuyết Chương 2: Dãy số. Cấp số cộng. Cấp số nhân
Lý thuyết Chương 3: Giới hạn. Hàm số liên tục

==== ~~~~~~ ====

Bài liên quan:

Leave a Comment Hủy