Lý thuyết Toán 12 Bài 9: Khoảng biến thiên và khoảng tứ phân vị
A. Lý thuyết Khoảng biến thiên và khoảng tứ phân vị
1. Khoảng biến thiên
Cho mẫu số liệu ghép nhóm:

trong đó các tần số và là cỡ mẫu
|
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là |
Ý nghĩa: Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc. Khoảng biến thiên được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán
2. Khoảng tứ phân vị
|
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu là , là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất của mẫu số liệu đó, tức là |
Ý nghĩa: Do khoảng tứ phân vị của mẫu số liệu ghép nhóm chỉ phụ thuộc vào nửa giữa của mẫu số liệu, nên không bị ảnh hưởng bởi các giá trị bất thường và có thể dùng đại lượng này để loại giá trị bất thường
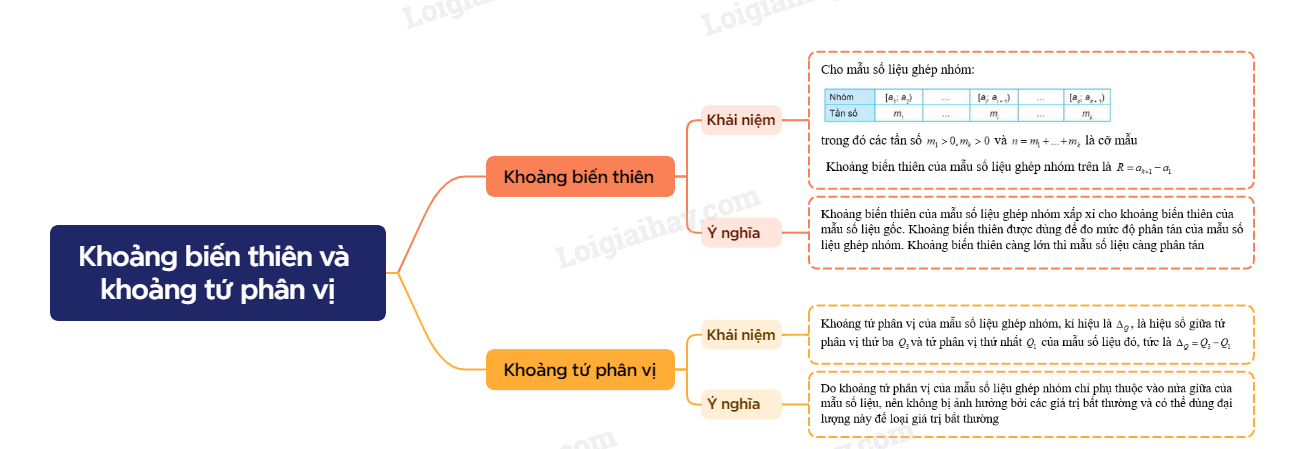
Sơ đồ tư duy Khoảng biến thiên và khoảng tứ phân vị
B. Bài tập Khoảng biến thiên và khoảng tứ phân vị
Bài 1. Khoảng biến thiên của mẫu số liệu ghép nhóm là:
A. Tổng số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.
B. Hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.
C. Tổng số giữa hai đầu mút của nhóm bất kì có chứa dữ liệu của mẫu số liệu.
D. Hiệu số giữa hai đầu mút của nhóm bất kì có chứa dữ liệu của mẫu số liệu.
Hướng dẫn giải
Đáp án đúng là: B
Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.
Bài 2. Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
A. Hiệu giữa tứ phân vị thứ ba và tứ phân vị thứ nhất của mẫu số liệu ghép nhóm đó.
B. Tổng giữa tứ phân vị thứ ba và tứ phân vị thứ nhất của mẫu số liệu ghép nhóm đó.
C. Hiệu giữa hai tứ phân vị bất kì của mẫu số liệu ghép nhóm đó.
D. Tổng giữa hai tứ phân vị bất kì của mẫu số liệu ghép nhóm đó.
Hướng dẫn giải
Đáp án đúng là: A
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là hiệu giữa tứ phân vị thứ ba và tứ phân vị thứ nhất của mẫu số liệu ghép nhóm đó.
(Dùng cho bài 3, 4) Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau:
|
Thời gian (phút) |
[0; 20) |
[20; 40) |
[40; 60) |
[60; 80) |
[80; 100) |
|
Số học sinh |
5 |
9 |
12 |
10 |
6 |
Bài 3. Tìm khoảng biến thiên của mẫu số liệu trên?
Hướng dẫn giải
Khoảng biến thiên của mẫu số liệu trên là R = 100 – 0 = 100.
Bài 4. Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên?
Hướng dẫn giải
Cỡ mẫu là n = 5 + 9 + 12 + 10 + 6 = 42.
Giả sử x1; …; x42 là thời gian tập thể dục của 42 học sinh và được xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất là x11. Mà x11 thuộc nhóm [20; 40) nên nhóm chứa tứ phân vị thứ nhất là [20;40).
Ta có .
Tứ phân vị thứ ba là x32. Mà x32 thuộc nhóm [60; 80). Do đó nhóm chứa tứ phân vị thứ ba là [60; 80).
.
Vậy .
Bài 5. Chiều cao của hai loài hoa được một người thống kê theo biểu đồ sau:
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên về chiều cao của loài hoa A và loài hoa B. Dựa vào khoảng tứ phân vị, hãy xác định xem chiều cao của loài hoa nào biến động nhiều hơn.
Hướng dẫn giải
Từ biểu đồ, ta có bảng số liệu ghép nhóm sau:
|
Chiều cao |
[100; 199) |
[200; 299) |
[300; 399) |
[400; 499) |
|
Loài A |
20 |
18 |
14 |
10 |
|
Loài B |
35 |
30 |
20 |
15 |
Xét loài A.
Cỡ mẫu là n = 20 + 18 + 14 + 10 = 62.
Giả sử x1; …; x62 là chiều cao của 62 cây hoa loài A và được xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu là x16 mà x16 [100; 199).
Do đó .
Tứ phân vị thứ ba của mẫu số liệu là x47 mà x47 [300; 399).
Do đó .
Vậy .
Xét loài B.
Cỡ mẫu n = 35 + 30 + 20 + 15 = 100.
Giả sử y1; …; y100 là chiều cao của 100 cây hoa loài B và được sắp theo thứ tự không giảm.
Tứ phân vị thứ nhất là , mà y25; y26 [100; 199).
Ta có .
Tứ phân vị thứ ba là , mà y75; y76 [300; 399).
Ta có .
Vậy .
Chiều cao của loài A có độ phân tán nhiều hơn.
Xem thêm các bài tóm tắt lý thuyết Toán lớp 12 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn
Lý thuyết Bài 6: Vectơ trong không gian
Lý thuyết Bài 7: Hệ trục toạ độ trong không gian
Lý thuyết Bài 8: Biểu thức toạ độ của các phép toán vectơ
Lý thuyết Bài 9: Khoảng biến thiên và khoảng tứ phân vị
Lý thuyết Bài 10: Phương sai và độ lệch chuẩn