Giải bài tập Toán lớp 8 Bài 11: Hình thoi
Trả lời câu hỏi giữa bài
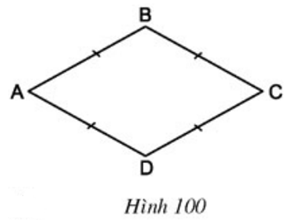
Câu hỏi 1 trang 104 Toán 8 Tập 1: Chứng minh rằng tứ giác ABCD trên Hình 100 cũng là một hình bình hành.
Lời giải
Tứ giác ABCD có các cặp cạnh đối bằng nhau
⇒ ABCD là hình bình hành
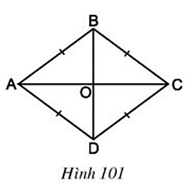
Câu hỏi 2 trang 104 Toán 8 Tập 1: Cho hình thoi ABCD, hai đường chéo cắt nhau tại O (h.101).
a) Theo tính chất của hình bình hành, hai đường chéo của hình thoi có tính chất gì?
b) Hãy phát hiện thêm các tính chất khác của hai đường chéo AC và BD.
Lời giải
a) Vì hình thoi có tất cả các tính chất của hình bình hành nên theo tính chất của hình bình hành, hai đường chéo của hình thoi có tính chất cắt nhau tại trung điểm mỗi đường
b) Xét ΔAOB và ΔCOB
AB = CB
BO chung
OA = OC (O là trung điểm AC )
⇒ ΔAOB = ΔCOB (c.c.c)
⇒ (các cặp góc tương ứng)
Với
Mà
Nếu
AC là phân giác của góc
Chứng minh tương tự, ta kết luận được:
AC, BD là các đường phân giác của các góc của hình thoi và AC ⊥ BD tại O
Câu hỏi 3 trang 105 Toán 8 Tập 1: Hãy chứng minh dấu hiệu nhận biết 3.
Lời giải
Dấu hiệu nhận biết 3: Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi

ABCD là hình bình hành ⇒ O là trung điểm AC và O là trung điểm BD
Xét và có:
OA chung
OB = OD (O là trung điểm BD)
⇒ ΔAOB = ΔAOD (hai cạnh góc vuông)
⇒ AB = AD (hai cạnh tương ứng)
Hình bình hành ABCD ⇒ AB = CD và AD = BC
Do đó AB = BC = CD = DA
⇒ ABCD là hình thoi.
Bài tập (trang 105, 106)
Bài 73 trang 105 Toán 8 Tập 1: Tìm các hình thoi trên hình 102.

Lời giải:
Các tứ giác ở hình 102a, b, c, e là hình thoi.
– Hình 102a:
Tứ giác ABCD là hình thoi vì có AB = BC = CD = DA
– Hình 102b:
Xét tứ giác EFGH, ta có:
EF = GH và EH = FG
⇒ EFGH là hình bình hành
Lại có EG là tia phân giác của
⇒ EFGH là hình thoi. (Dấu hiêu 4).
– Hình 102c:
Xét tứ giác KINM, ta có:
Hai đường chéo IM, KN cắt nhau tại trung điểm mỗi đường.
⇒ IKMN là hình bình hành
Lại có IM ⊥ KN
⇒ IKMN là hình thoi. (Dấu hiệu 3).
– Hình 102e:
Xét tứ giác ADBC là hình thoi vì:
AC = AD = AB (C, B, D cùng thuộc đường tròn tâm A).
BC = BA = BD (A, C, D cùng thuộc đường tròn tâm B)
⇒ AC = CB = BD = DA
⇒ ACBD là hình thoi.
– Tứ giác trên hình 102d không là hình thoi vì 4 cạnh không bằng nhau.
Bài 74 trang 106 Toán 8 Tập 1: Hai đường chéo của một hình thoi bằng 8cm và 10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:
A. 6cm;
B. cm;
C. cm;
D. 9 cm.
Lời giải:

Giả sử ta có hình thoi ABCD thỏa mãn yêu cầu bài toán, trong đó đường chéo AC = 8cm, BD = 10cm.
Gọi ABCD O là giao điểm hai đường chéo
⇒ O là trung điểm của AC và BD.
Xét vuông tại O, ta có:
(định lý Py – ta – go)
Vậy chọn đáp án là B.
Bài 75 trang 106 Toán 8 Tập 1: Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi.
Lời giải:

+) Xét tam giác ABD có:
E là trung điểm của AB
H là trung điểm của AD
⇒ EH là đường trung bình của tam giác ADB
(1)
+) Xét tam giác ABC có:
E là trung điểm của AB
F là trung điểm của BC
⇒ EF là đường trung bình của tam giác ABC
(2)
+) Xét tam giác BCD có:
F là trung điểm của BC
G là trung điểm của DC
⇒ FG là đường trung bình của tam giác BCD
(3)
+) Xét tam giác CDA có:
H là trung điểm của AD
G là trung điểm của DC
⇒ HG là đường trung bình của tam giác CDA
(4)
Ta lại có ABCD là hình chữ nhật nên AC = BD (5)
Từ (1), (2), (3), (4) và (5) suy ra EF = FG = GH= HE
⇒Tứ giác EFGH là hình thoi.
Bài 76 trang 106 Toán 8 Tập 1: Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.
Lời giải:

+) Xét tam giác ABC có:
E là trung điểm của AB
F là trung điểm của BC
⇒ EF là đường trung bình của tam giác ABC
(1)
+) Xét tam giác CDA có:
H là trung điểm của AD
G là trung điểm của DC
⇒ HG là đường trung bình của tam giác CDA
(2)
Từ (1) và (2) suy ra EF // HG và EF = HG
⇒Tứ giác EFGH là hình bình hành
Ta lại có:
EF // AC
BD ⊥ AC
Suy ra BD ⊥ EF (3)
Xét tam giác ABD có:
E là trung điểm của AB
H là trung điểm của AD
⇒ EH là đường trung bình của tam giác ADB
(4)
Từ (3) và (4) suy ra: EF ⊥ EH
Hình bình hành EFGH có nên là hình chữ nhật
Bài 77 trang 106 Toán 8 Tập 1:Chứng minh rằng:
a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.
b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.
Lời giải:

a) Gọi O là giao điểm của hai đường chéo của hình thoi ABCD
Vì ABCD là hình thoi nên ABCD là hình bình hành
Mà tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
Suy ra O là tâm đối xứng của hình thoi ABCD.
b)
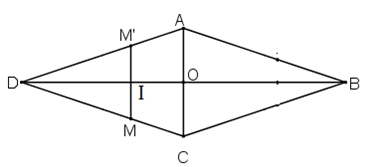
Xét hình thoi ABCD, gọi O là giao điểm của 2 đường chéo.
* Ta chứng minh: đường chéo BD là trục đối xứng của hình
Lấy điểm M bất kì thuộc hình thoi. Không mất tổng quát, M nằm trên CD.
Gọi M’ đối xứng với M qua đường thẳng BD. Ta chứng minh điểm M’ cũng thuộc hình thoi
+ Gọi I là giao điểm của MM’ và BD.
Xét tam giác DIM và DIM’ có:
DI chung
IM= IM’ ( do M và M’ đối xứng với nhau qua BD)
∆DIM = ∆DIM’ ( c.g.c)
và DM = DM’
Lại có: ABCD là hình thoi nên (DB là phân giác ) hay
Mà
Suy ra điểm M’ nằm trên cạnh AD hay điểm M’ thuộc hình thoi
Do đó BD là trục đối xứng của hình thoi.
Chứng minh tương tự, ta có: AC là trục đối xứng của hình thoi.
Vậy hai đường chéo AC, BD là hai trục đối xứng của hình thoi.
Bài 78 trang 106 Toán 8 Tập 1: Đố. Hình 103 biểu diễn một phần của cửa xếp, gồm những thanh kim loại dài bằng nhau và được liên kết với nhau bởi các chốt tại hai đầu và tại trung điểm. Vì sao tại mỗi vị trí của cửa xếp, các tứ giác trên hình vẽ đều là hình thoi, các điểm chốt I, K, M, N, O nằm trên một đường thẳng?
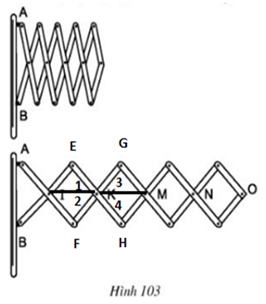
Lời giải:
Ta có hình vẽ minh họa như sau:
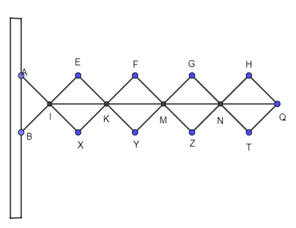
Tứ giác IEKX là hình thoi nên KI là phân giác
Tứ giác KFMY là hình thoi nên KM là phân giác
Mà (hai góc đối đỉnh)
Suy ra KI trùng KM
Suy ra K, I, M thẳng hàng (1).
Tứ giác KFMY là hình thoi nên MK là phân giác
Tứ giác MGNZ là hình thoi nên MN là phân giác
Mà (hai góc đối đỉnh)
Suy ra MK trùng MN
Suy ra K, M, N thẳng hàng (2).
Tứ giác MGNZ là hình thoi nên NM là phân giác
Tứ giác HQTN là hình thoi nên NQ là phân giác
Mà (hai góc đối đỉnh)
Suy ra NM trùng NQ
Suy ra Q, M, N thẳng hàng (3).
Từ (1), (2) và (3) suy ra các điểm I, K, M, N, O cùng nằm trên một đường thẳng.