Giải bài tập Toán lớp 8 Ôn tập chương 4 Đại số
Trả lời câu hỏi giữa bài
Câu hỏi 1 trang 52 Toán 8 Tập 2: Cho ví dụ về bất đẳng thức theo từng loại có chứa dấu <, ≤, > và ≥.
Trả lời:
– Bất đẳng thức chứa dấu < là -8 < (-2) + 7
– Bất đẳng thức chứa dấu ≤ là 6 + (-2) ≤ 8
– Bất đẳng thức chứa dấu > là 6 > (-1) + 5
– Bất đẳng thức chứa dấu ≥ là 11 + 2 ≥ 7
Câu hỏi 2 trang 52 Toán 8 Tập 2: Bất phương trình bậc nhất một ẩn có dạng như thế nào? Cho ví dụ.
Trả lời:
Bất phương trình bậc nhất một ẩn có dạng: ax + b < 0 (hoặc ax + b > 0, ax + b ≤ 0, ax + b ≥ 0) trong đó a, b là hai số đã cho, a ≠ 0.
Ví dụ: 3x + 9 < 0 (hoặc 2x + 8 > 0, -2x + 3 ≤ 0, x + 9 ≥ 0)
Câu hỏi 3 trang 52 Toán 8 Tập 2: Hãy chỉ ra một nghiệm của bất phương trình trong ví dụ của câu hỏi 2.
Trả lời:
Ví dụ: 3x + 9 < 0
⇔ 3x < – 9 ⇔ x < -3
Ví dụ -5 là một nghiệm của bất phương trình này.
Câu hỏi 4 trang 52 Toán 8 Tập 2: Phát biểu quy tắc chuyển vế để biến đổi bất phương trình. Quy tắc này dựa trên tính chất nào của thứ tự trên tập số?
Trả lời:
Quy tắc chuyển vế: Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta phải đổi dấu của hạng tử đó.
Quy tắc này dựa trên tính chất liên hệ giữa thứ tự và phép cộng trên tập số (sgk trang 36 Toán 8 Tập 2):
Khi cộng cùng một số vào cả hai vế của một bất đẳng thức ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Câu hỏi 5 trang 52 Toán 8 Tập 2: Phát biểu quy tắc nhân để biến đổi bất phương trình. Quy tắc này dựa trên tính chất nào của thứ tự trên tập số?
Trả lời:
Quy tắc nhân: Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
– Giữ nguyên chiều bất phương trình nếu số đó dương;
– Đổi chiều bất phương trình nếu số đó âm.
Quy tắc này dựa trên tính chất liên hệ giữa thứ tự và phép nhân trên tập số (sgk trang 36 Toán 8 Tập 2):
– Khi nhân cả hai vế của bất đẳng thức với cùng một số dương ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
– Khi nhân cả hai vế của bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho
Bài tập (trang 53; 54)
Bài 38 trang 53 Toán 8 Tập 2: Cho m > n. Chứng minh:
a) m + 2 > n + 2;
b) -2m < – 2n;
c) 2m – 5 > 2n – 5;
d) 4 – 3m < 4 – 3n.
Lời giải:
a) Ta có: m > n ⇒ m + 2 > n + 2 (cộng hai vế với 2, bất đẳng thức không đổi chiều)
b) Ta có: m > n
⇒ -2m < -2n (nhân hai vế với -2 và đổi chiều bất đẳng thức)
c) m > n ⇒ 2m > 2n (nhân hai vế với 2, bất đẳng thức không đổi chiều)
⇒ 2m – 5 > 2n – 5 (cộng hai vế với -5, bất đẳng thức không đổi chiều)
d) m > n ⇒ -3m < -3n (nhân hai vế với -3 và đổi chiều bất đẳng thức)
⇒ 4 – 3m < 4 – 3n (cộng hai vế với 4, bất đẳng thức không đổi chiều)
Bài 39 trang 53 Toán 8 Tập 2: Kiểm tra xem -2 là nghiệm của bất phương trình nào trong các bất phương trình sau:
a) -3x + 2 > -5;
b) 10 – 2x < 2;
c) x2 – 5 < 1;
d) |x| < 3;
e) |x| > 2;
f) x + 1 > 7 – 2x.
Lời giải:
Lần lượt thay x = -2 vào từng bất phương trình:
a) Vế trái = -3x + 2 = -3.(-2) + 2 = 8
Vì 8 > -5 nên x = -2 là nghiệm của bất phương trình -3x + 2 > -5.
b) Vế trái = 10 – 2x = 10 – 2.(-2) = 10 + 4 = 14
Vì 14 > 2 nên x = -2 không phải nghiệm của bất phương trình 10 – 2x < 2.
c) Vế trái = x2 – 5 = (-2)2 – 5 = 4 – 5 = -1
Vì -1 < 1 nên x = -2 là nghiệm của bất phương trình x2 – 5 < 1.
d)Vế trái = |x| = |-2| = 2
Vì 2 < 3 nên x = -2 là nghiệm của bất phương trình |x| < 3.
e) Vế trái = |x| = |-2| = 2
Vì 2 = 2 nên x = -2 không phải nghiệm của bất phương trình |x| > 2.
f) Vế trái = x + 1 = -2 + 1 = -1.
Vế phải = 7 – 2x = 7 – 2.(-2) = 7 + 4 = 11
Vì -1 < 11 nên x = -2 không phải nghiệm của bất phương trình x + 1 > 7 – 2x.
Bài 40 trang 53 Toán 8 Tập 2: Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
a) x – 1 < 3;
b) x + 2 > 1;
c) 0,2x < 0,6;
d) 4 + 2x < 5.
Lời giải:
a) x – 1 < 3
⇔ x < 3 + 1 (Chuyển vế và đổi dấu hạng tử -1)
⇔ x < 4
Vậy bất phương trình có nghiệm x < 4.
Biểu diễn tập nghiệm trên trục số:

b) x + 2 > 1
⇔ x > 1 – 2
⇔ x > -1.
Vậy bất phương trình có nghiệm x > -1.
Biểu diễn tập nghiệm trên trục số:
![]()
c) 0,2x < 0,6
⇔ 5.0,2x < 5.0,6
⇔ x < 3.
Vậy bất phương trình có nghiệm x < 3.
Biểu diễn tập nghiệm trên trục số:

d) 4 + 2x < 5
⇔ 2x < 5 – 4
⇔ 2x < 1
⇔
Vậy bất phương trình có nghiệm .
Biểu diễn tập nghiệm trên trục số:
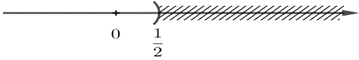
Bài 41 trang 53 Toán 8 Tập 2: Giải các bất phương trình:
a) ;
b) ;
c) ;
d) .
Lời giải:
a) ;
⇔ 2 – x < 5.4 (Nhân cả hai vế với 4 > 0, bất phương trình không đổi dấu)
⇔ 2 – x < 20
⇔ 2 – 20 < x (Chuyển vế và đổi dấu hạng tử -x và 20)
⇔ -18 < x hay x > -18.
Vậy bất phương trình có nghiệm x > -18.
b) ;
⇔ 3.5 ≤ 2x + 3 (Nhân cả hai vế với 5 > 0, bất phương trình không đổi dấu)
⇔ 15 ≤ 2x + 3
⇔ -2x ≤ 3 – 15 (Chuyển vế và đổi dấu hạng tử 15; 2x)
⇔ -2x ≤ -12
⇔ x ≥ 6 (Chia cả hai vế cho -2 < 0, bất phương trình đổi dấu)
Vậy bất phương trình có nghiệm x ≥ 6.
c) ;
( nhân cả hai vế với 15 > 0, bất phương trình không đổi dấu).
⇔ 5(4x – 5) > 3(7 – x)
⇔ 20x – 25 > 21 – 3x
⇔ 20x + 3x > 21 + 25 (chuyển vế hạng tử – 25; – 3x)
⇔ 23x > 46
(nhân cả hai vế với > 0, nên bất phương trình không đổi dấu).
⇔ x > 2
Vậy nghiệm của bất phương trình đã cho là x > 2 .
d) .
(nhân cả hai vế với 12 > 0, bất phương trình không đổi dấu).
⇔ -3(2x + 3) ≥ -4(4 – x )
⇔ -6x – 9 ≥ -16 + 4x
⇔ 16 – 9 ≥ 4x + 6x (Chuyển vế và đổi dấu hạng tử -6x và -16)
⇔ 7 ≥ 10x
⇔ 0,7 ≥ x (chia cả hai vế cho 10 > 0, bất phương trình không đổi dấu)
hay x ≤ 0,7
Vậy bất phương trình có nghiệm x ≤ 0,7.
Bài 42 trang 53 Toán 8 Tập 2: Giải các bất phương trình:
a) 3 – 2x > 4;
b) 3x + 4 < 2 ;
c) (x – 3)2 < x2 – 3;
d) (x – 3)(x + 3) < (x + 2)2 + 3.
Lời giải:
a) 3 – 2x > 4
⇔ -2x > 4 – 3
⇔ -2x > 1 (Chuyển vế và đổi dấu hạng tử 3)
⇔ (Chia cả hai vế cho -2 < 0, BPT đổi chiều)
Vậy bất phương trình có nghiệm .
b) 3x + 4 < 2
⇔ 3x < 2 – 4 (Chuyển vế và đổi dấu hạng tử 4)
⇔ 3x < -2
⇔ (Chia cả hai vế cho 3 > 0, BPT không đổi chiều)
Vậy bất phuong trình có nghiệm .
c) (x – 3)2 < x2 – 3
⇔ x2 – 6x + 9 < x2 – 3
⇔ x2 – 6x – x2 < -3 – 9
⇔ -6x < -12
⇔ x > 2 (Chia cả hai vế cho -6 < 0, BPT đổi chiều)
Vậy bất phương trình có nghiệm x > 2.
d) (x – 3)(x + 3) < (x + 2)2 + 3
⇔ x2 – 9 < x2 + 4x + 4 + 3
⇔ x2 – x2 – 4x < 4+ 3 + 9 (Chuyển vế và đổi dấu các hạng tử)
⇔ -4x < 16
⇔ x > -4 (Chia cả hai vế cho -4 < 0, BPT đổi chiều).
Vậy bất phương trình có nghiệm x > -4.
Bài 43 trang 53-54 Toán 8 Tập 2: Tìm x sao cho:
a) Giá trị của biểu thức 5 – 2x là số dương;
b) Giá trị của biểu thức x + 3 nhỏ hơn giá trị của biểu thức 4x – 5;
c) Giá trị của biểu thức 2x + 1 không nhỏ hơn giá trị của biểu thức x + 3;
d) Giá trị của biểu thức x2 + 1 không lớn hơn giá trị của biểu thức (x – 2)2;
Lời giải:
a) Để giá trị biểu thức 5 – 2x là số dương
⇔ 5 – 2x > 0
⇔ -2x > -5 (Chuyển vế và đổi dấu hạng tử 5)
⇔ (Chia cả hai vế cho -2 < 0, BPT đổi chiều)
Vậy để giá trị biểu thức 5 – 2x là số dương thì .
b) Để giá trị của biểu thức x + 3 nhỏ hơn giá trị biểu thức 4x – 5 thì:
x + 3 < 4x – 5
⇔ x – 4x < -3 – 5 ( chuyển vế và đổi dấu các hạng tử 4x và 3 )
⇔ -3x < -8
⇔ (Chia cả hai vế cho -3 < 0, BPT đổi chiều).
Vậy để giá trị của biểu thức x + 3 nhỏ hơn giá trị biểu thức 4x – 5 thì .
c) Để giá trị của biểu thức 2x +1 không nhỏ hơn giá trị của biểu thức x + 3 thì:
2x + 1 ≥ x + 3
⇔ 2x – x ≥ 3 – 1 (chuyển vế và đổi dấu các hạng tử 1 và x).
⇔ x ≥ 2.
Vậy để giá trị của biểu thức 2x +1 không nhỏ hơn giá trị của biểu thức x + 3 thì x ≥ 2.
d) Để giá trị của biểu thức x2 + 1 không lớn hơn giá trị của biểu thức (x – 2)2 thì:
x2 + 1 ≤ (x – 2)2
⇔ x2 + 1 ≤ x2 – 4x + 4
⇔ x2 – x2 + 4x ≤ 4 – 1 ( chuyển vế và đổi dấu hạng tử 1; x2 và – 4x).
⇔ 4x ≤ 3
⇔ ( chia cả hai vế cho 4 > 0, BPT không đổi chiều)
Vậy để giá trị của biểu thức x2 + 1 không lớn hơn giá trị của biểu thức (x – 2)2 thì .
Bài 44 trang 54 Toán 8 Tập 2: Đố:
Trong một cuộc thi đố vui, ban tổ chức quy định mỗi người dự thi phải trả lời 10 câu hỏi ở vòng sơ tuyển. Mỗi câu hỏi này có sẵn 4 đáp án, nhưng trong đó chỉ có 1 đáp án đúng. Người dự thi chọn đáp án đúng sẽ được 5 điểm, chọn đáp án sai sẽ bị trừ 1 điểm. Ở vòng sơ tuyển Ban tổ chức tặng cho mỗi người thi 10 điểm và quy định người nào có tổng số điểm từ 40 trở lên mới được dự thi ở vòng tiếp theo. Hỏi người dự thi phải trả lời chính xác bao nhiêu câu hỏi ở vòng sơ tuyển thì mới được dự thi tiếp ở vòng sau?
Lời giải:
Gọi x là số câu trả lời đúng (0 ≤ x ≤ 10, x ∈ )
Số câu trả lời sai: 10 – x
Trả lời đúng x câu được 5x (điểm), trả lời sai 10 – x (câu) bị trừ (10 – x) điểm.
Do đó, sau khi trả lời 10 câu thì người dự thi sẽ có: 5x – (10 – x) + 10
Để được dự thi tiếp vòng sau thì:
5x – (10 – x) + 10 40.
5x – 10 + x + 10 40
Vậy người dự thi phải trả lời chính xác ít nhất 7 câu hỏi thì mới được dự thi ở vòng sau.
Bài 45 trang 54 Toán 8 Tập 2: Giải các phương trình:
a) |3x| = x + 8;
b) |-2x| = 4x + 8;
c) |x – 5| = 3x;
d) |x + 2| = 2x – 10.
Lời giải:
a) |3x| = x + 8 (1)
+ TH1: Xét x ≥ 0, khi đó |3x| = 3x
(1) ⇔ 3x = x + 8
⇔ 3x – x = 8
⇔ 2x = 8
⇔ x = 4 > 0 (thỏa mãn)
+ TH2: Xét x < 0, khi đó |3x| = -3x
(1) ⇔ -3x = x + 8
⇔ -3x – x = 8
⇔ -4x = 8
⇔ x = -2 < 0 (thỏa mãn)
Vậy phương trình có tập nghiệm S = {4; -2}.
b) |-2x| = 4x + 18 (2)
+ TH1: xét x > 0, khi đó – 2x < 0 nên |-2x| = 2x
(2) ⇔ 2x = 4x + 18
⇔ 2x – 4x = 18
⇔ -2x = 18
⇔ x = -9 < 0 (không thỏa mãn điều kiện)
+ TH2: Xét x ≤ 0, khi đó -2x ≥ 0 nên |-2x| = -2x
(2) ⇔ -2x = 4x + 18
⇔ -2x – 4x = 18
⇔ -6x = 18
⇔ x = -3 < 0 (thỏa mãn)
Vậy phương trình có tập nghiệm S = {-3}.
c) |x – 5| = 3x (3)
+ TH1: Xét x ≥ 5, khi đó x – 5 ≥ 0 nên |x – 5| = x – 5
(3) ⇔ x – 5 = 3x
⇔ x – 3x = 5
⇔ -2x = 5
⇔ x = -2,5 < 5 ( không thỏa mãn điều kiện)
+ TH2: Xét x < 5, khi đó x – 5 < 0 nên |x – 5| = -(x – 5)
(3) ⇔ -(x – 5) = 3x
⇔ -x + 5 = 3x
⇔ -x – 3x = -5
⇔ -4x = -5
⇔ (thỏa mãn)
Vậy phương trình có tập nghiệm .
d) |x + 2| = 2x – 10 (4)
+ TH1: Xét x ≥ -2, khi đó x + 2 ≥ 0 nên |x + 2| = x + 2
(4) ⇔ x + 2 = 2x – 10
⇔ 2 + 10 = 2x – x
⇔ 12 = x hay x = 12 > -2 (thỏa mãn)
+ TH2: Xét x < -2, khi đó x + 2 < 0 nên |x + 2| = -(x + 2)
(4) ⇔ -(x + 2) = 2x – 10
⇔ -x – 2 = 2x – 10
⇔ -x – 2x = -10 + 2
⇔ -3x = -8
⇔ (không thỏa mãn điều kiện)
Vậy phương trình có tập nghiệm S = {12}.