Tuyển tập đề thi học kì 2 môn Toán 8 trường Amsterdam

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tóm tắt tài liệu

Bộ đề toán lớp 8 qua các năm của trường Hà Nội – Amsterdam có lời giải chi tiết.

Đề 7

Câu 1. Cho biểu thức $A = 2 + \frac{{8{x^2} + 24x}}{{{x^2} – 6x + 9}}:(\frac{{x + 3}}{x} – \frac{2}{{3 – x}} + \frac{{15 – {x^2}}}{{{x^2} – 3x}})$

a) Rút gọn A.

b) Tìm x thỏa mãn A>0

c) Tìm x sao cho |A|= 3 – 3x.

Câu 2. Một xưởng đóng giày theo kế hoạch phải hoàn thành số giày quy định trong 26 ngày, nhưng vì làm việc có hiệu quả vượt mức 5 chiếc một ngày nên sau 24 ngày chẳng những hoàn thành kế hoạch mà còn vượt mức 60 chiếc giày. Tính số giày mà xưởng phải đóng theo quy định.

Câu 3. Cho $\widehat {xAy} = {90^0}$. Một điểm O cố định trên tia Ay , điểm C di động trên tia Ax , vẽ$\Delta COB$vuông ở O sao cho OC=2 OB . Gọi E và D lần lượt là hình chiếu vuông góc của O và B trên tia BC và Ay .
a) Chứng minh CA.DB=AO.DO
b) Chứng minh

c) Tính $\frac{{O{B^2}}}{{B{C^2}}}$. Nếu ${S_{\Delta AED}} = 9c{m^2}$, tính EA, ED.

d) Chứng minh rằng khi C di động trên tia Ax thì B di động trên một tia cố định

Câu 4. a) Tìm giá trị nhỏ nhất của biểu thức $P = 25({x^2} + {y^2}) + {(12 – 3x – 4y)^2}.$

b) Cho $\Delta ABC$, các đường cao cắt nhau tại H. Gọi S là diện tích $\Delta ABC$. Chứng minh rằng: AB² +HC² =BC² +AH² =AC² +HB² và AB. HC+BC . HA +AC. HB =4S.

c) Cho a, b, c >0 và a² +b² +c² =1. Chứng minh $\frac{a}{{{b^2} + {c^2}}} + \frac{b}{{{c^2} + {a^2}}} + \frac{c}{{{a^2} + {b^2}}} \ge \frac{{3\sqrt 3 }}{2}.$

Hướng dẫn giải đề thi học kì II trường Hà Nội – Amsterdam

Câu 1. Cho biểu thức $A = 2 + \frac{{8{x^2} + 24x}}{{{x^2} – 6x + 9}}:(\frac{{x + 3}}{x} – \frac{2}{{3 – x}} + \frac{{15 – {x^2}}}{{{x^2} – 3x}})$

a) Rút gọn A.

b) Tìm x thỏa mãn A>0

c) Tìm x sao cho |A|= 3 – 3x.

Lời giải

a) Điều kiện: $x \ne 0,x \ne 3$. Khi đó, ta có:

$A = 2 + \frac{{8{x^2} + 24x}}{{{x^2} – 6x + 9}}:(\frac{{x + 3}}{x} – \frac{2}{{3 – x}} + \frac{{15 – {x^2}}}{{{x^2} – 3x}})$

$ \Leftrightarrow A = 2 + \frac{{8x(x + 3)}}{{{{(x – 3)}^2}}}:\frac{{(x + 3)(x – 3) + 2x + 15 – {x^2}}}{{x(x – 3)}}$

$ \Leftrightarrow A = 2 + \frac{{8x(x + 3)}}{{{{(x – 3)}^2}}}:\frac{{{x^2} – 9 + 2x + 15 – {x^2}}}{{x(x – 3)}}$

$ \Leftrightarrow A = 2 + \frac{{8x(x + 3)}}{{{{(x – 3)}^2}}}:\frac{{2(x + 3)}}{{x(x – 3)}}$

$ \Leftrightarrow A = 2 + \frac{{8x(x + 3)}}{{{{(x – 3)}^2}}}.\frac{{x(x – 3)}}{{2(x + 3)}}$

$ \Leftrightarrow A = 2 + \frac{{4{x^2}}}{{x – 3}} = \frac{{4{x^2} + 2x – 6}}{{x – 3}}$

Vậy $A = \frac{{4{x^2} + 2x – 6}}{{x – 3}}$

b) Ta có:

A>0 $ \Leftrightarrow \frac{{4{x^2} + 2x – 6}}{{x – 3}} > 0$

$ \Leftrightarrow \frac{{4(x – 1)(x + \frac{3}{2})}}{{x – 3}} > 0$

$ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}(x – 1)(x + \frac{3}{2}) > 0\\x – 3 > 0\end{array} \right.\\\left\{ \begin{array}{l}(x – 1)(x + \frac{3}{2}) < 0\\x – 3 < 0\end{array} \right.\end{array} \right.$

$ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}\left[ \begin{array}{l}x – 1 < x + \frac{3}{2} < 0\\0 < x – 1 < x + \frac{3}{2}\end{array} \right.\\x > 3\end{array} \right.\\\left\{ \begin{array}{l}x – 1 < 0 < x + \frac{3}{2}\\x – 3 < 0\end{array} \right.\end{array} \right.$

$(do\,\,x – 1 < x + \frac{3}{2})$

$ \Leftrightarrow \left[ \begin{array}{l}x > 3\\ – \frac{3}{2} < x < 1\end{array} \right.$

Vậy A>0 $ \Leftrightarrow \left[ \begin{array}{l}x > 3\\ – \frac{3}{2} < x < 1\end{array} \right.$

c) Ta có:

|A|=3 – 3x$ \Leftrightarrow |\frac{{2(x – 1)(2x + 3)}}{{x – 3}}| = 3(1 – x)$

Điều kiện: $x \le 1,x \ne 0$

Trường hợp 1:

$\frac{{2(x – 1)(2x + 3)}}{{x – 3}} = 3(1 – x)$

$ \Leftrightarrow 2(x – 1)(2x + 3) = – 3(x – 1)(x – 3)$

$ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \frac{3}{7}\end{array} \right.$

So với điều kiện ta nhận x = a, $x = \frac{3}{7}$

Trường hợp 2:

$\frac{{2(x – 1)(2x + 3)}}{{x – 3}} = – 3(1 – x)$

$ \Leftrightarrow 2(x – 1)(2x + 3) = 3(x – 1)(x – 3)$

$ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = – 15\end{array} \right.$

So với điều kiện ta nhận x = 1 , x = -15 .

Vậy |A|=3 – 3x khi x=1 hoặc $x = \frac{3}{7};x = – 15$

Câu 2. Một xưởng đóng giày theo kế hoạch phải hoàn thành số giày quy định trong 26ngày, nhưng vì làm việc có hiệu quả vượt mức 5 chiếc một ngày nên sau 24 ngày chẳng những hoàn thành kế hoạch mà còn vượt mức 60 chiếc giày. Tính số giày mà xưởng phải đóng theo quy định.

Lời giải

Gọi số giày mà xưởng phải đóng theo quy định là x (chiếc), điều kiện $x \in {\mathbb{N}^*}$.

Năng suất theo kế hoạch của xưởng là $\frac{x}{{26}}$( chiếc/ ngày)

Năng suất thực tế của xưởng là $\frac{x}{{26}} + 5$( chiếc/ ngày)

Số giày xưởng sản suất trong 24 ngày là $24(\frac{x}{{26}} + 5)$ (chiếc)

Do xưởng hoàn thành xong kế hoạch trong 24 ngày và vượt mức 60 chiếc giày nên ta có phương trình:

$\begin{array}{l}24(\frac{x}{{26}} + 5) – x = 60 \Leftrightarrow x(1 – \frac{{12}}{{13}}) = 60\\ \Leftrightarrow \frac{1}{{13}}x = 60 \Leftrightarrow x = 780\end{array}$

(nhận)

Vậy số giày mà xưởng phải đóng theo kế hoạch là: 780 (chiếc).

Câu 3. Cho$\widehat {xAy} = {90^0}$. Một điểm O cố định trên tia Ay , điểm C di động trên tia Ax , vẽ$\Delta COB$vuông ở O sao cho OC=2 OB . Gọi E và D lần lượt là hình chiếu vuông góc của O và B trên tia BC và Ay .
a) Chứng minh CA.DB=AO.DO
b) Chứng minh

c) Tính$\frac{{O{B^2}}}{{B{C^2}}}$. Nếu ${S_{\Delta AED}} = 9c{m^2}$, tính EA, ED.

d) Chứng minh rằng khi C di động trên tia Ax thì B di động trên một tia cố định

Lời giải

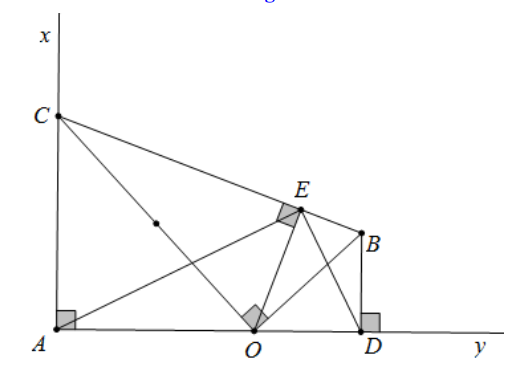
Tuyển tập đề thi học kì 2 môn Toán 8 trường Amsterdam (ảnh 1)

a) Chứng minh CA. DB = AO. DO.

Ta có:

$\widehat {AOC} + \widehat {BOC} + \widehat {BOD} = {180^0}$

$ \Rightarrow \widehat {AOC} + {90^0} + \widehat {BOD} = {180^0}$

$ \Rightarrow \widehat {AOC} + \widehat {BOD} = {90^0}$

Mà $\widehat {AOC} + \widehat {ACO} = {90^0}$(vì $\Delta COA$vuông ở A)

Do đó \[\widehat {ACO} = \widehat {BOD}\]

Xét $\Delta ACO$ và $\Delta DOB$

\[\widehat {ACO} = \widehat {BOD}\](chứng minh trên)

\[\widehat {CAO} = \widehat {ODB} = {90^0}\]

$\Rightarrow Δ A C O ∽ Δ D O B (g - g)$

$ \Rightarrow \frac{{AC}}{{DO}} = \frac{{AO}}{{DB}} \Rightarrow CA.DB = AO.DO.$

b) Chứng minh

\[\widehat {ECO} + \widehat {EBO} = {90^0}\](vì $\Delta COB$vuông ở O)

\[\widehat {EOB} + \widehat {EBO} = {90^0}\]( vì $\Delta EOB$vuông ở E)

$ \Rightarrow \widehat {EOB} = \widehat {ECO}.$

Xét $\Delta ECO$và $\Delta EOB:$

\[\widehat {EOB} = \widehat {ECO}\](chứng minh trên)

\[\widehat {CEO} = \widehat {OEB} = {90^0}\]

$ \Rightarrow \frac{{EC}}{{EO}} = \frac{{CO}}{{OB}} = 2.(1)$

Ta có:

Từ (1) và (2), ta có:$\frac{{EC}}{{EO}} = \frac{{AC}}{{DO}} = 2.$

Ta có:

$\left\{ \begin{array}{l}\widehat {EOB} = \widehat {ECO}\\\widehat {BOD} = \widehat {ACO}\end{array} \right. \Rightarrow \widehat {EOB} + \widehat {BOD} = \widehat {ECO} + \widehat {ACO} \Leftrightarrow \widehat {ACE} = \widehat {DOE}$

Xét $\Delta ACE$và $\Delta DOE:$

\[\frac{{EC}}{{EO}} = \frac{{AC}}{{DO}} = 2\]

\[\widehat {ACE} = \widehat {DOE}\]

$\Rightarrow Δ A C E ∽ Δ D O E (c - g - c)$ .

c) Tính \[\frac{{O{B^2}}}{{B{C^2}}}.\]Nếu ${S_{\Delta AED}} = 9c{m^2}$, tính EA, ED.

Xem thêm

Bài liên quan:

Leave a Comment Hủy