Thế nào là hai lực cân bằng? Nếu dùng hai vecto để biểu diến hai lực cân bằng thì hai vecto này có mối quan hệ gì với nhau?

Câu hỏi:

Thế nào là hai lực cân bằng? Nếu dùng hai vecto để biểu diến hai lực cân bằng thì hai vecto này có mối quan hệ gì với nhau?

Trả lời:

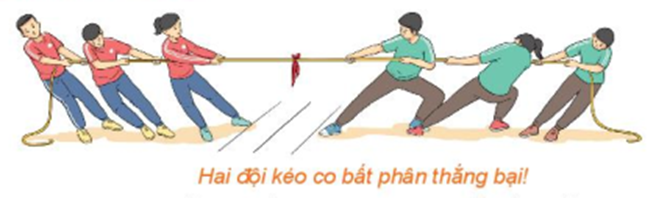
Nếu chỉ có hai lực tác dụng vào cùng một vật mà vật vẫn đứng yên thì hai lực đó là hai lực cân bằng.
Ví dụ: Hai đội kéo co cùng kéo sợi dây. Nếu hai đội mạnh ngang nhau thì họ sẽ tác dụng lên dây hai lực cân bằng. Sợi dây chịu tác dụng của hai lực cân bằng thì sẽ đứng yên.
 

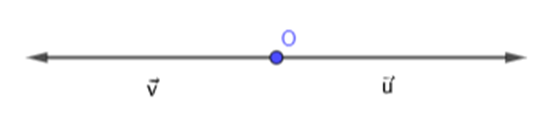
Hai vecto $\overrightarrow{u}$ và $\overrightarrow{v}$ biểu diễn cho hai vecto cân bằng thì hai vecto này có chung gốc, ngược hướng và có độ lớn (hay độ dài) bằng nhau.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Một con tàu chuyển động từ bờ bên này sang bờ bên kia của một dòng sông với vận tốc riêng không đổi. Giả sử vận tốc dòng nước là không đổi và không đáng kể, các yếu tố bên ngoài tác động không ảnh hưởng đến vận tốc thực tế của tàu. Nếu không quan tâm đến điểm đến thì cần giữ lái cho tàu tạo với bờ sông một góc bao nhiêu để tàu sang bờ bên kia được nhanh nhất?
   
   

   Câu hỏi:
   

   Một con tàu chuyển động từ bờ bên này sang bờ bên kia của một dòng sông với vận tốc riêng không đổi. Giả sử vận tốc dòng nước là không đổi và không đáng kể, các yếu tố bên ngoài tác động không ảnh hưởng đến vận tốc thực tế của tàu. Nếu không quan tâm đến điểm đến thì cần giữ lái cho tàu tạo với bờ sông một góc bao nhiêu để tàu sang bờ bên kia được nhanh nhất?
   

   Trả lời:

   

   Sau bài học này ta sẽ giải quyết bài toán này như sau:
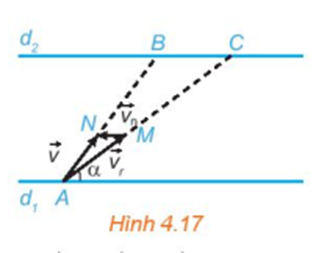
   Ta biểu thị hai bờ sông là hai đường thẳng song song d₁, d₂ (H.4.17). Giả sử tàu xuất phát từ $A\in d_1$ và bánh lái luôn được giữ để tàu tạo với bờ một góc $\alpha$. Gọi  và  lần lượt là vận tốc riêng của tàu và vận tốc dòng nước. Gọi M, N là các điểm sao cho $\overrightarrow{v_r}=\overrightarrow{AM},\overrightarrow{v_n}=\overrightarrow{MN}.$
   Khi đó tàu chuyển động với vecto vận tốc thực tế là $\overrightarrow{v}=\overrightarrow{v_r}+\overrightarrow{v_n}=\overrightarrow{AM}+\overrightarrow{MN}=\overrightarrow{AN}.$
   Gọi B, C tương ứng là giao điểm của AN, AM với d₂. Tàu chuyển động thẳng từ A đến B với vận tốc thực tế là $\overrightarrow{AN}$, do đó thời gian cần thiết để tàu sang được bờ d₂ là $\frac{AB}{AN}=\frac{AC}{AM}$. Mặt khác, $AM=\left|\overrightarrow{v_r}\right|$ không đổi nên $\frac{AC}{AM}$ nhỏ nhất ⇔ AC nhỏ nhất $\iff AC\perp d_2\iff AM\perp d_2.$
   Vậy để tàu sang được bờ bên kia nhanh nhất, ta giữ bánh lái để tàu luôn vuông góc với bờ.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

2. Với hai vecto a→,b→ cho trước, lấy một điểm A và vẽ các vecto AB→=a→,BC→=b→. Lấy một điểm A’ khác A cũng vẽ các vecto A’B’→=a→,B’C’→=b→. Hỏi hai vecto AC→,A’C’→ có mối quan hệ gì?
   
   

   Câu hỏi:
   

   Với hai vecto $\overrightarrow{a},\overrightarrow{b}$ cho trước, lấy một điểm A và vẽ các vecto $\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{BC}=\overrightarrow{b}.$ Lấy một điểm A’ khác A cũng vẽ các vecto $\overrightarrow{A‘B‘}=\overrightarrow{a},\overrightarrow{B‘C‘}=\overrightarrow{b}.$ Hỏi hai vecto $\overrightarrow{AC},\overrightarrow{A‘C‘}$ có mối quan hệ gì?
   

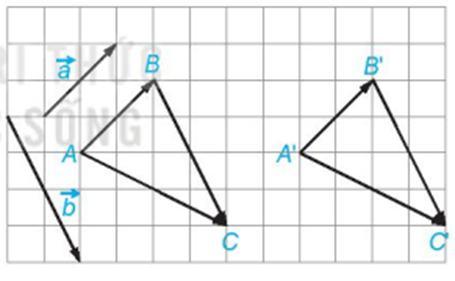
   Trả lời:

   Ta có: $\overrightarrow{AB}=\overrightarrow{a}$
   $\Rightarrow \overrightarrow{AB}$ cùng hướng với $\overrightarrow{a}$  và độ dài $\overrightarrow{AB}$  bằng độ dài $\overrightarrow{a}$.
   Ta lại có: $\overrightarrow{A‘B‘}=\overrightarrow{a}$
   $\Rightarrow \overrightarrow{A‘B‘}$ cùng hướng với $\overrightarrow{a}$  và độ dài $\overrightarrow{A‘B‘}$  bằng độ dài $\overrightarrow{a}$.
   $\Rightarrow \overrightarrow{AB}$ cùng hướng với $\overrightarrow{A‘B‘}$ và độ dài $\overrightarrow{AB}$ bằng độ dài $\overrightarrow{A‘B‘}$.
   $\Rightarrow \overrightarrow{AB}=\overrightarrow{A‘B‘}\iff$ ABB’A’ là hình bình hành  (1)
   Ta có: $\overrightarrow{BC}=\overrightarrow{b}$
   $\Rightarrow \overrightarrow{BC}$ cùng hướng với $\overrightarrow{b}$  và độ dài $\overrightarrow{BC}$ bằng độ dài $\overrightarrow{b}$.
   Ta lại có:
   $\Rightarrow \overrightarrow{B‘C‘}$ cùng hướng với $\overrightarrow{b}$ và độ dài $\overrightarrow{B‘C‘}$ bằng độ dài .
   $\Rightarrow \overrightarrow{BC}$ cùng hướng với $\overrightarrow{B‘C‘}$ và độ dài $\overrightarrow{BC}$ bằng độ dài $\overrightarrow{B‘C‘}$.
   $\Rightarrow \overrightarrow{BC}=\overrightarrow{B‘C‘}\iff$ BB’C’C là hình bình hành $\iff \overrightarrow{CC‘}=\overrightarrow{BB‘}$  (2)
   Từ (1) và (2) suy ra $\overrightarrow{\text{AA}‘}=\overrightarrow{CC‘}\iff$AA’C’C là hình bình hành
   $\Rightarrow \overrightarrow{AC}=\overrightarrow{A‘C‘}$
   Vậy $\overrightarrow{AC}=\overrightarrow{A‘C‘}$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

3. Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vecto AB→+AD→ và AC→.
   
   

   Câu hỏi:
   

   Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vecto $\overrightarrow{AB}+\overrightarrow{AD}$ và $\overrightarrow{AC}$.
   

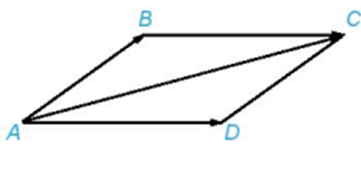
   Trả lời:

   Vì ABCD là hình bình hành nên ta có: $\overrightarrow{AD}=\overrightarrow{BC}$
   $\Rightarrow \overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$

   Vậy $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

4. a) Trong Hình 4.14a, hãy chỉ ra các vecto a→+b→  và vecto b→+a→ . b) Trong Hình 4,14b, hãy chỉ ra các vecto a→+b→+c→  và vecto a→+b→+c→ .
   
   

   Câu hỏi:
   

   a) Trong Hình 4.14a, hãy chỉ ra các vecto $\overrightarrow{a}+\overrightarrow{b}$  và vecto $\overrightarrow{b}+\overrightarrow{a}$ .
   b) Trong Hình 4,14b, hãy chỉ ra các vecto $\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}$  và vecto $\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)$ .
   

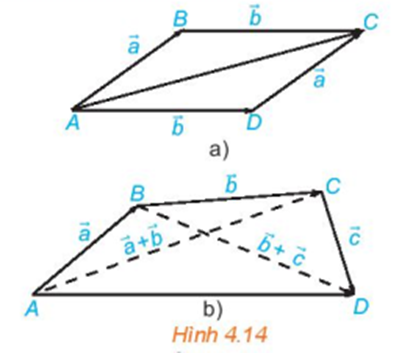
   Trả lời:

   Trong Hình 4.14a:
   Ta có: $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$

   $\overrightarrow{b}+\overrightarrow{a}=\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AC}$
   $\Rightarrow \overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}$
   Trong Hình 4.14b: 
   Ta có: $\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}=\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}$
   $\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AD}$
   $\Rightarrow \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

5. Cho hình thoi ABCD với cạnh có độ dài bằng 1 và BAD^=1200. Tính độ dài của các vecto CB→+CD→,DB→+CD→+BA→
   
   

   Câu hỏi:
   

   Cho hình thoi ABCD với cạnh có độ dài bằng 1 và $\widehat{BAD}={120}^0$. Tính độ dài của các vecto $\overrightarrow{CB}+\overrightarrow{CD},\overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BA}$
   

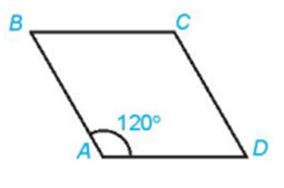
   Trả lời:

   

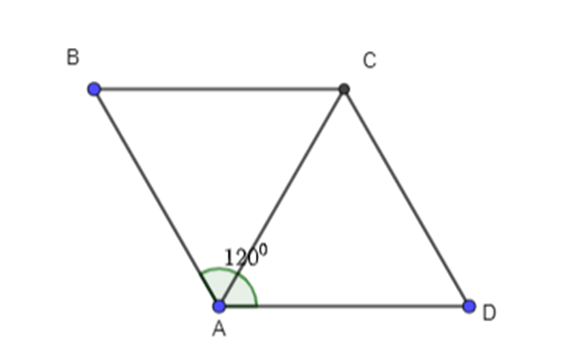
   Vì ABCD là hình thoi nên AC là tia phân giác $\widehat{BAC}$

   $\Rightarrow \widehat{BAC}=\widehat{CAD}=\frac{\widehat{BAD}}{2}=\frac{{120}^0}{2}={60}^0$
   Xét ΔABC có AB = BC và $\widehat{BAC}={60}^0$
   ⇒ ΔABC đều
   ⇒ AC = AB = BC = 1
   Ta có:
   $\overrightarrow{CB}+\overrightarrow{CD}=\overrightarrow{CA}$ (quy tắc hình bình hành)
   $\Rightarrow \left|\overrightarrow{CB}+\overrightarrow{CD}\right|=\left|\overrightarrow{CA}\right|=CA=1$
   $\overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BA}=\overrightarrow{CD}+\overrightarrow{DB}+\overrightarrow{BA}=\overrightarrow{CB}+\overrightarrow{BA}=\overrightarrow{CA}$ (quy tắc ba điểm).
   $\Rightarrow \left|\overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BA}\right|=\left|\overrightarrow{CA}\right|=CA=1$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====