Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên. Dựa theo các khoảng cách đã cho trên Hình 6, tính khoảng cách giữa Châu Đốc và Rạch Giá.

Câu hỏi:

Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên. Dựa theo các khoảng cách đã cho trên Hình 6, tính khoảng cách giữa Châu Đốc và Rạch Giá.

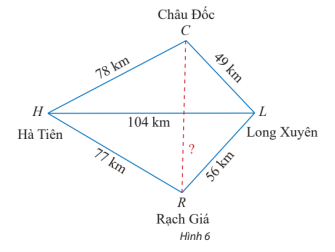
Trả lời:

Áp dụng hệ quả của định lí côsin cho tam giác CHL ta có:
cos $\widehat{CLH}$ = 
$\frac{C{L}^2+H{L}^2-C{H}^2}{2.CL.HL}=\frac{{49}^2+{104}^2-{78}^2}{\mathrm{2.49.104}}\approx 0,6999$
⇒ $\widehat{CLH}$ ≈ 45°35′.
Áp dụng hệ quả của định lí côsin cho tam giác RHL ta có:
cos $\widehat{RLH}$ = 
$\frac{R{L}^2+H{L}^2-R{H}^2}{2.RL.HL}=\frac{{56}^2+{104}^2-{77}^2}{\mathrm{2.56.104}}\approx 0,6888$
⇒  $\widehat{RLH}$ ≈ 46°28′.
Suy ra $\widehat{CLR}=\widehat{CLH}+\widehat{RLH}\approx {45}^{o}35’+{46}^{o}28’\approx {92}^{o}3‘$
Áp dụng định lí côsin cho tam giác LCR ta có:
CR² = CL² + LR² – 2.CL.LR.cos$\widehat{CLR}$ = 49² + 56² – 2.49.56.cos92^o3’ ≈ 5 733,3
⇒ CR ≈ 75,7.
Vậy khoảng cách giữa Châu Đốc và Rạch Giá khoảng 75,7 km.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Với số liệu đo được từ một bên bờ sông như hình vẽ bên, bạn hãy giúp nhân viên đo đạc tính khoảng cách giữa hai cái cây bên kia bờ sông.
   
   

   Câu hỏi:
   

   Với số liệu đo được từ một bên bờ sông như hình vẽ bên, bạn hãy giúp nhân viên đo đạc tính khoảng cách giữa hai cái cây bên kia bờ sông.
   

   Trả lời:

   Gọi vị trí của người đo đạc đứng là điểm A và gọi B, C lần lượt là vị trí hai cái cây bên kia sông. Ta có tam giác ABC với AC = 100 m ; AB = 75 m và $\widehat{A}={32}^o$ .
   

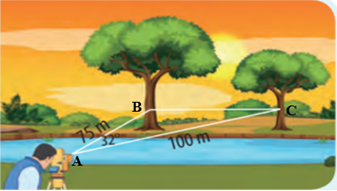
   Áp dụng định lí côsin cho tam giác ABC ta có :
   BC² = AB² + AC² – 2.AB.AC.cosA = 75² + 100² – 2.75.100.cos32° ≈ 2 904,3.
   ⇒ BC ≈ $\sqrt{2904,3}$  ≈ 53,9 m.
   Vậy hai cái cây bên kia sông cách nhau khoảng 53,9 m.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

2. Giải tam giác ABC trong các trường hợp sau: a) a = 17,4; B^=44o30′;  C^=64o . b) a = 10; b = 6; c = 8.
   
   

   Câu hỏi:
   

   Giải tam giác ABC trong các trường hợp sau:
   a) a = 17,4; $\widehat{B}={44}^{o}30‘;\widehat{C}={64}^o$ .
   b) a = 10; b = 6; c = 8.

   Trả lời:

   a) Tam giác ABC có:
   $\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{A}={180}^o-(\widehat{B}+\widehat{C})={180}^o-({44}^{o}30‘+{64}^o)={71}^{o}30‘$
   Áp dụng định lí sin ta có:
    $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\Rightarrow \frac{17,4}{\sin {71}^{o}30‘}=\frac{b}{\sin {44}^{o}30‘}=\frac{c}{\sin {64}^o}$

   Suy ra:
    $b=\frac{17,4.\sin {44}^{o}30‘}{\sin {71}^{o}30‘}\approx 12,9$; $c=\frac{17,4.\sin {64}^o}{\sin {71}^{o}30‘}\approx 16,5$
   Vậy tam giác ABC có: $\widehat{A}={71}^{o}30‘$ ; $\widehat{B}={44}^{o}30‘;\widehat{C}={64}^o$ ; a = 17,4; b ≈ 12,9; c ≈ 16,5.
   b) Áp dụng hệ quả của định lí côsin ta có:
   cosA = $\frac{b^2+c^2-a^2}{2bc}=\frac{6^2+8^2-{10}^2}{\mathrm{2.6.8}}=\frac{0}{96}=0$  
   ⇒ $\widehat{A}={90}^o$ .
   cosB = $\frac{a^2+c^2-b^2}{2ac}=\frac{{10}^2+8^2-6^2}{\mathrm{2.10.8}}=\frac{128}{160}=0,8$  
   ⇒ $\widehat{B}\approx {36}^{o}52‘$ .
   $\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{C}={180}^o-(\widehat{A}+\widehat{B})={180}^o-({90}^o+{36}^{o}52‘)={53}^{o}8‘$
   Vậy tam giác ABC có: $\widehat{A}={90}^o$ ; $\widehat{B}={36}^{o}52‘$ ; $\widehat{C}={53}^{o}8‘$ ; a = 10; b = 6; c = 8.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

3. Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với vận tốc 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc 25° về phía tây với tốc độ 630 km/h (Hình 5). Sau 90 phút, hai máy bay cách nhau bao nhiêu kilômét? Giả sử chúng đang ở cùng độ cao.
   
   

   Câu hỏi:
   

   Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với vận tốc 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc 25° về phía tây với tốc độ 630 km/h (Hình 5). Sau 90 phút, hai máy bay cách nhau bao nhiêu kilômét? Giả sử chúng đang ở cùng độ cao.
   

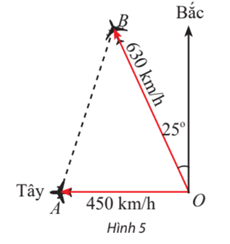
   Trả lời:

   Gọi A và B lần lượt là vị trí của hai máy bay sau khi cất cánh 90 phút.
   Đổi 90 phút = 1,5 giờ.
   Sau 90 phút (tức là sau 1,5 giờ) chiếc máy bay di chuyển theo hướng tây đi được quãng đường là: 450.1,5 = 675 km, tức là OA = 675 km.
   Sau 90 phút (tức là sau 1,5 giờ) chiếc máy bay di chuyển theo hướng lệch bắc 25° về phía tây đi được quãng đường là: 630.1,5 = 945 km, tức là OB = 945 km.
   Ta có $\widehat{AOB}={90}^o-{25}^o={65}^o$ .
   Áp dụng định lí côsin cho tam giác OAB ta có:
   AB² = OA² + OB² – 2.OA.OB.cos  = 675² + 945² – 2.675.945.cos65^o ≈ 809 494,8
   ⇒ AB = $\sqrt{809494,8}\approx 899,7$ .
   Vậy sau 90 phút hai máy bay cách nhau khoảng 899,7 km.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

4. Giải tam giác ABC trong các trường hợp sau: a) AB = 14, AC = 23, A^=125o ; b) BC = 22, B^=64o,  C^=38o ; c) AC = 22, B^=120o,  C^=28o ; d) AB = 23, AC = 32, BC = 44.
   
   

   Câu hỏi:
   

   Giải tam giác ABC trong các trường hợp sau:
   a) AB = 14, AC = 23, $\widehat{A}={125}^o$ ;
   b) BC = 22, $\widehat{B}={64}^o,\widehat{C}={38}^o$ ;
   c) AC = 22, $\widehat{B}={120}^o,\widehat{C}={28}^o$ ;
   d) AB = 23, AC = 32, BC = 44.

   Trả lời:

   a) Áp dụng định lí côsin cho tam giác ABC ta có:
   BC² = AB² + AC² – 2.AB.AC.cosA = 14² + 23² – 2.14.23.cos125° ≈ 1 094,4.
   ⇒ BC ≈ $\sqrt{1094,4}\approx 33,1$ .
   Áp dụng hệ quả của định lí côsin cho tam giác ABC ta có:
   cosB =  $\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC}=\frac{{14}^2+33,1^2-{23}^2}{\mathrm{2.14.33},1}\approx 0,823$
   ⇒ $\widehat{B}\approx {34}^{o}37‘$
   Mặt khác tam giác ABC có:
   $\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{C}={180}^o-(\widehat{A}+\widehat{B})={180}^o-({125}^o+{34}^{o}37‘)={20}^{o}23‘$
   Vậy tam giác ABC có:
   AB = 14, AC = 23, BC ≈ 33,1; $\widehat{A}={125}^o$; $\widehat{B}\approx {34}^{o}37‘$; $\widehat{C}\approx {20}^{o}23‘$ .
   b) Tam giác ABC có:
   $\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{A}={180}^o-(\widehat{B}+\widehat{C})={180}^o-({64}^o+{38}^o)={78}^o$
   Áp dụng định lí sin cho tam giác ABC ta có:
   $\frac{BC}{\sin A}=\frac{AC}{\sin B}=\frac{AB}{\sin C}\Rightarrow \frac{22}{\sin {78}^o}=\frac{AC}{\sin {64}^o}=\frac{AB}{\sin {38}^o}$

   Suy ra: $AC=\frac{22.\sin {64}^o}{\sin {78}^o}\approx 20,2$ ; $AB=\frac{22.\sin {38}^o}{\sin {78}^o}\approx 13,8$
   Vậy tam giác ABC có:
   $\widehat{A}={78}^o;\widehat{B}={64}^o,\widehat{C}={38}^o$; AB ≈ 13,8; AC ≈ 20,2; BC = 22.
   c) Tam giác ABC có:
   $\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{A}={180}^o-(\widehat{B}+\widehat{C})={180}^o-({120}^o+{28}^o)={32}^o$
   Áp dụng định lí sin cho tam giác ABC ta có:
   $\frac{BC}{\sin A}=\frac{AC}{\sin B}=\frac{AB}{\sin C}\Rightarrow \frac{BC}{\sin {32}^o}=\frac{22}{\sin {120}^o}=\frac{AB}{\sin {28}^o}$

   Suy ra: $BC=\frac{22.\sin {32}^o}{\sin {120}^o}\approx 13,5$; $AB=\frac{22.\sin {28}^o}{\sin {120}^o}\approx 11,9$  
   Vậy tam giác ABC có:
   $\widehat{A}={32}^o;\widehat{B}={120}^o,\widehat{C}={28}^o$; AB ≈ 11,9; AC = 22; BC = 13,5.
   d) Áp dụng hệ quả của định lí côsin ta có:
   cosA =  $\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}=\frac{{23}^2+{32}^2-{44}^2}{\mathrm{2.23.32}}=\frac{-383}{1472}\approx -0,26$
   ⇒ $\widehat{A}\approx {105}^{o}4‘$
   cosB =
    $\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC}=\frac{{23}^2+{44}^2-{32}^2}{\mathrm{2.23.44}}=\frac{1441}{2024}\approx 0,712$
   ⇒ $\widehat{B}={44}^{o}36‘$
   $\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{C}={180}^o-(\widehat{A}+\widehat{B})={180}^o-({105}^{o}4‘+{44}^{o}36‘)={30}^{o}20‘$
   Vậy tam giác ABC có: $\widehat{A}\approx {105}^{o}4‘$; $\widehat{B}={44}^{o}36‘$; $\widehat{C}={30}^{o}20‘$; AB = 23, AC = 32, BC = 44.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

5. Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8 km. Góc tạo bởi hai đoạn dây AC và CB là 70°. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.
   
   

   Câu hỏi:
   

   Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8 km. Góc tạo bởi hai đoạn dây AC và CB là 70°. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.
   

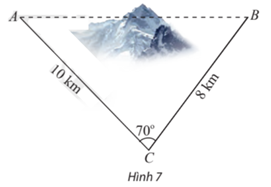
   Trả lời:

   Áp dụng định lí côsin cho tam giác ABC ta có:
   AB² = AC² + BC² – 2.AC.BC.cosC = 10² + 8² – 2.10.8.cos70° ≈ 109,3
   ⇒ AB ≈ $\sqrt{109,3}\approx 10,5$
   Ta có : (AC + CB) – AB =(10 + 8) – 10,5 = 7,5.
   Vậy vì không thể nối trực tiếp từ A đến B nên chiều dài dây tăng thêm 7,5 km.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====