Trong mỗi hình dưới đây, hãy tính R theo a và sin A.

Câu hỏi:

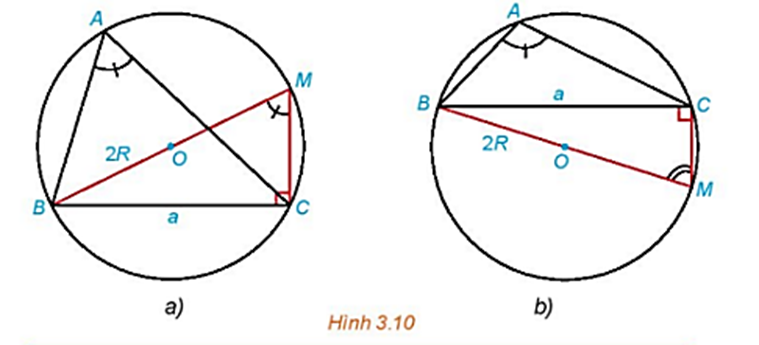
Trong mỗi hình dưới đây, hãy tính R theo a và sin A.

Trả lời:

Hình 3.10a):

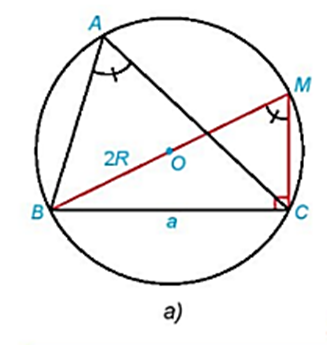
Xét ΔBCM vuông tại C, có:
$\sin \widehat{BMC}=\frac{BC}{BM}=\frac{a}{2R}$
Mà $\widehat{BMC}=\widehat{A}$ (hai góc nội tiếp cùng chắn $\stackrel{⏜}{BC}$)
$\Rightarrow \sin A=\frac{a}{2R}$

Hình 3.10b):

Xét ΔBCM vuông tại C, có:
$\sin \widehat{BMC}=\frac{BC}{BM}=\frac{a}{2R}$
Mà $\widehat{BMC}+\widehat{A}=\frac{1}{2}sđ\stackrel{⏜}{BAC}+\frac{1}{2}sđ\stackrel{⏜}{BMC}=\frac{1}{2}{.360}^0={180}^0\Rightarrow \widehat{BMC}={180}^0-\widehat{A}$
$\Rightarrow \sin A=\sin \left({180}^0-\widehat{BMC}\right)=\sin \widehat{BMC}=\frac{a}{2R}$

$\Rightarrow R=\frac{a}{2\sin A}.$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Ngắm tháp rùa từ bờ, chỉ với những dụng cụ đơn giản, dễ chuẩn bị, ta cũng có thể xác định được khoảng cách từ vị trí ta đứng tới Tháp Rùa. Em có biết vì sao?
   
   

   Câu hỏi:
   

   Ngắm tháp rùa từ bờ, chỉ với những dụng cụ đơn giản, dễ chuẩn bị, ta cũng có thể xác định được khoảng cách từ vị trí ta đứng tới Tháp Rùa. Em có biết vì sao?

   Trả lời:

   Sau bài này ta sẽ trả lời được:
   

   Theo các bước sau, ta có thể xác định được khoảng cách từ vị trí A trên bờ hồ Hoàn Kiếm đến Tháp Rùa.
   Bước 1. Trên bờ, đặt một cọc tiêu tại vị trí A và một cọc tiêu tại vị trí B nào đó. Đo khoảng cách AB.
   Bước 2. Đứng tại A, ngắm Tháp Rùa và một cọc tiêu tại ví trí B nào đó để đo góc tạo bởi hai hướng ngắm đó.
   Bước 3. Đứng tại B, ngắm Tháp Rùa và một cọc tiêu tại ví trí A để đo góc tạo bởi hai hướng ngắm đó.
   Bước 4. Gọi C là vị trí của Tháp Rùa. Áp dụng định lí sin cho tam giác ABC để tính độ dài cạnh AC.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

2. Một tàu biển xuất phát từ cảng Vân Phong (Khánh Hòa) theo hướng đông với vận tốc 20km/h. Sau khi đi được 1 giờ, tàu chuyển sang hướng Đông Nam rồi giữ nguyên vận tốc và đi tiếp. a) Hãy vẽ sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát (1km trên thực tế ứng với 1cm trên bản vẽ). b) Hãy đo trực tiếp trên bản vẽ và cho biết sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng Vân Phong bao nhiêu kilômét (số đo gần đúng). c) Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì có thể dùng Định lí Pythagore (Pi – ta – go) để tính chính xác các số đo trong câu b hay không?
   
   

   Câu hỏi:
   

   Một tàu biển xuất phát từ cảng Vân Phong (Khánh Hòa) theo hướng đông với vận tốc 20km/h. Sau khi đi được 1 giờ, tàu chuyển sang hướng Đông Nam rồi giữ nguyên vận tốc và đi tiếp.
   a) Hãy vẽ sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát (1km trên thực tế ứng với 1cm trên bản vẽ).
   b) Hãy đo trực tiếp trên bản vẽ và cho biết sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng Vân Phong bao nhiêu kilômét (số đo gần đúng).
   c) Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì có thể dùng Định lí Pythagore (Pi – ta – go) để tính chính xác các số đo trong câu b hay không?

   Trả lời:

   a) Sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát là:
   

   Trong đó vị trí A là vị trí là vị trí cảng Vân Phong.
   b) Sau khi đi 1h theo hướng đông với vận tốc 20km/h thì tàu đi đến vị trí B, đi tiếp 0,5 giờ còn lại theo hướng đông nam cũng với vận tốc 20km/h thì tàu đến vị trí C. Tiến hành đo đoạn AC ta thấy xấp xỉ 27,9 cm.
   Vậy sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng vân phong 27,9 km.
   c)
   

   Sau khi đi 1h theo hướng đông với vận tốc 20km/h thì tàu đi đến vị trí B, quãng đường AB là: 20.1 = 20 (km).
   Còn 1h còn lại, tàu đi theo hướng nam với vận tốc 20km/h thì tàu đi đến vị trí B, quãng đường BC là: 20.1 = 20 (km).
   Do hướng đông hợp với hướng nam một góc 90⁰ nên $\widehat{ABC}={90}^0$.
   Xét tam giác ABC vuông tại B, ta có:
   BC² = AB² + AC² (định lý Py – ta – go)
   BC² = 20² + 20²
   BC² = 400 + 400
   BC² = 800
   $BC=20\sqrt{2}\approx 28,28\left(km\right)$
   Vậy sau khi đi được 2 giờ, tàu chuyển sang hướng nam thay thì có thể dùng định lí Py – ta – go tính chính xác được ví trí của tàu lúc này cách cảng Vân Phong 28,28 km.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

3. Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập công thức tính a theo b, c và giá trị lượng giác của góc A. a) Tính a2 theo BD2 và CD2. b) Tính a2 theo b, c và DA. c) Tính DA theo c và cosA. d) Chứng minh a2 = b2 + c2 – 2bc.cosA.
   
   

   Câu hỏi:
   

   Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập công thức tính a theo b, c và giá trị lượng giác của góc A.
   a) Tính a² theo BD² và CD².
   b) Tính a² theo b, c và DA.
   c) Tính DA theo c và cosA.
   d) Chứng minh a² = b² + c² – 2bc.cosA.
   

   Trả lời:

   a) Xét ΔBDC vuông tại D, có:
   BC² = BD² + DC² (py – ta – go)
   Hay a² = BD² + DC²
   b) Xét ΔBDA vuông tại D, có:
   BA² = BD² + DA² (py – ta – go)
   Hay BD² = c² – DA²
   Ta lại có: DC = DA + b
   Khi đó: a² = c² – DA² + (DA + b)² = c² – DA² + DA² + 2.DA.b + b² = c² + b² + 2.DA.b.
   Vậy a² = c² + b² + 2.DA.b (1)
   c) Xét ΔBDA vuông tại D, có:
   $DA=c.\cos \alpha$
   d) Thay $DA=c.\cos \alpha$ vào biểu thức (1), ta được:
   a² = c² + b² + 2.c.b.$cos\alpha$ (đpcm).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

4. Định lý Pythagore có phải là một trường hợp đặc biệt của định lý côsin hay không?
   
   

   Câu hỏi:
   

   Định lý Pythagore có phải là một trường hợp đặc biệt của định lý côsin hay không?

   Trả lời:

   Xét tam giác ABC vuông tại A, ta có:
   BC² = AB² + AC² – 2AB.AC.cosA (định lí cos)
   = AB² + AC² – 2AB.AC.cos90⁰
   = AB² + AC² (định lí Py – ta – go)
   Định lý Pythagore có là một trường hợp đặc biệt của định lý côsin.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

5. Từ định lý côsin hãy viết các công thức tính cosA, cosB, cosC theo độ dài các cạnh a, b, c của tam giác ABC.
   
   

   Câu hỏi:
   

   Từ định lý côsin hãy viết các công thức tính cosA, cosB, cosC theo độ dài các cạnh a, b, c của tam giác ABC.

   Trả lời:

   Từ định lý cosin, ta có công thức tính cosA, cosB, cosC theo độ dài các cạnh a, b, c của tam giác ABC là:
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====