Câu hỏi:
Cho hàm số \(f\left( x \right)\) liên tục trên R và hàm số \(f’\left( x \right)\) có bảng biến thiên như sau. Tìm mệnh đề đúng?

A. Hàm số \(y = f\left( x \right)\) có 2 điểm cực tiểu và 1 điểm cực đại .
Đáp án chính xác
B. Hàm số \(y = f\left( x \right)\) có 1 điểm cực tiểuvà 1 điểm cực đại .
C. Hàm số không có giá trị lớn nhất và không có giá trị nhỏ nhất.
D. Hàm số \(y = f\left( x \right)\) có 1 điểm cực tiểu và 2 điểm cực đại .
Trả lời:
Dựa vào bảng biến thiên của \(f’\left( x \right),\) ta có \(f’\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_1} \in \left( { – \infty ; – 1} \right)\\x = {x_2} \in \left( { – 1;1} \right)\\x = {x_3} \in \left( {1; + \infty } \right)\end{array} \right..\)
\(f’\left( x \right)\)đổi dấu từ âm sang dương khi đi qua điểm \({x_1},\) suy ra \({x_1}\) là điểm cực tiểu.
\(f’\left( x \right)\) đổi dấu từ dương sang âm khi đi qua điểm \({x_2},\) suy ra \({x_2}\) là điểm cực đại.
\(f’\left( x \right)\) đổi dấu từ âm sang dương khi đi qua điểm \({x_3},\) suy ra \({x_3}\) là điểm cực tiểu.
Đáp án A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đồ thị của hàm số nào dưới đây có dạng đường cong trong hình vẽ sau?
Câu hỏi:
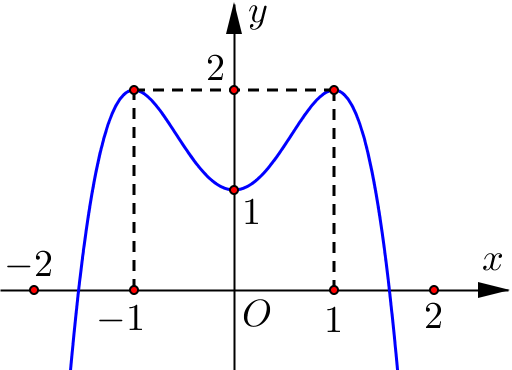
Đồ thị của hàm số nào dưới đây có dạng đường cong trong hình vẽ sau?
A. \(y = 2{x^4} – {x^2} + 1\).
Đáp án chính xác
B. \(y = – {x^4} + {x^2} + 1\).
C. \(y = – {x^4} + 2{x^2} + 1\).
D. \(y = {x^4} – 2{x^2} + 1\).
Trả lời:
Dựa vào đồ thị ta có đồ thị trên là đồ thị hàm bậc bốn trùng phương có bề lõm hướng xuống nên hệ số \(a < 0\) nên loại đáp án A và D.
Xét điểm \(\left( {1;2} \right)\) thuộc đồ thị hàm số trên.
Thay \(\left( {1;2} \right)\) vào \(y = – {x^4} + {x^2} + 1\) ta được 2 =1 (vô lý).
Thay \(\left( {1;2} \right)\) vào \(y = – {x^4} + 2{x^2} + 1\) ta được 2 = 2 (đúng).
Nên đồ thị trong hình vẽ trên là đồ thị của hàm số \(y = – {x^4} + 2{x^2} + 1.\)
Đáp án A====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số nghiệm của phương trình\(\frac{{\sin 2x}}{{\cos x + 1}} = 0\) trên đoạn \(\left[ {0;2020\pi } \right]\) là
Câu hỏi:
Số nghiệm của phương trình\(\frac{{\sin 2x}}{{\cos x + 1}} = 0\) trên đoạn \(\left[ {0;2020\pi } \right]\) là
A. \(3030\)
B. 2020
C. 3031
Đáp án chính xác
D. 4040
Trả lời:
Điều kiện: \(\cos x + 1 \ne 0 \Leftrightarrow x \ne \pi + l2\pi \left( {l \in \mathbb{Z}} \right)\).
Ta có:
\(\frac{{\sin 2x}}{{\cos x + 1}} = 0 \Leftrightarrow \sin 2x = 0 \Leftrightarrow 2x = k\pi \left( {k \in \mathbb{Z}} \right) \Leftrightarrow x = k\frac{\pi }{2}\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + m\pi \left( {m \in \mathbb{Z}} \right)\\x = n2\pi \left( {n \in \mathbb{Z}} \right)\\x = \pi + p2\pi \left( {p \in \mathbb{Z}} \right)\end{array} \right.\)
So lại với điều kiện, phương trình có họ nghiệm là \(\left[ \begin{array}{l}x = \frac{\pi }{2} + m\pi \left( {m \in \mathbb{Z}} \right)\\x = n2\pi \left( {n \in \mathbb{Z}} \right)\end{array} \right..\)
Xét \(0 \le \frac{\pi }{2} + m\pi \le 2020\pi \Leftrightarrow – \frac{\pi }{2} \le m\pi \le \frac{{4039}}{2}\pi \Leftrightarrow – \frac{1}{2} \le m \le \frac{{4039}}{2}.\) Vì \(m \in \mathbb{Z}\) nên có 2002 giá trị \(m\) thỏa mãn đề bài.
Xét \(0 \le n2\pi \le 2020\pi \Leftrightarrow 0 \le n\pi \le 1010.\) Vì \(n \in \mathbb{Z}\) nên có 1011 giá trị \(n\) thỏa mãn đề bài.
Vậy phương trình có tổng cộng 3031 nghiệm trên đoạn \(\left[ {0;2020\pi } \right].\)
Đáp án C====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số nghiệm của phương trình \({\log _4}\left( {3{x^2} + x} \right) = \frac{1}{2}\) là
Câu hỏi:
Số nghiệm của phương trình \({\log _4}\left( {3{x^2} + x} \right) = \frac{1}{2}\) là
A. \(1\).
B. \(5\).
C. \(0\).
D. \(2\).
Đáp án chính xác
Trả lời:
Ta có \({\log _4}\left( {3{x^2} + x} \right) = \frac{1}{2} \Leftrightarrow 3{x^2} + x = 2\)
\( \Leftrightarrow 3{x^2} + x – 2 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = – 1\\x = – \frac{2}{3}\end{array} \right..\)
Vậy phương trình có hai nghiệm.
Đáp án D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Với \(a\) là số thực dương khác \(1\) tùy ý, \({\log _{{a^5}}}{a^4}\) bằng
Câu hỏi:
Với \(a\) là số thực dương khác \(1\) tùy ý, \({\log _{{a^5}}}{a^4}\) bằng
A. \(\frac{1}{5}\).
B. \(\frac{4}{5}\).
Đáp án chính xác
C. \(20\).
D. \(\frac{5}{4}\).
Trả lời:
Ta có \({\log _{{a^5}}}{a^4} = \frac{4}{5}{\log _a}a = \frac{4}{5}.\)
Đáp án B====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Khối chóp có một nửa diện tích đáy là \(S\), chiều cao là \(2h\) thì có thể tích là:
Câu hỏi:
Khối chóp có một nửa diện tích đáy là \(S\), chiều cao là \(2h\) thì có thể tích là:
A. \(V = \frac{1}{2}S.h\).
B. \(V = \frac{1}{3}S.h\).
C. \(V = S.h\).
D. \(V = \frac{4}{3}S.h\).
Đáp án chính xác
Trả lời:
Áp dụng công thức thể tích khối chóp ta có: \(V = \frac{1}{3}.2S.2h = \frac{4}{3}S.h\)
Vậy chọn đáp án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====