Câu hỏi:
Cho hình chóp tứ giác \(S.ABCD\) có \(SA = x\) và tất cả các cạnh còn lại đều bằng 1. Khi thể tích khối chóp \(S.ABCD\) đạt giá trị lớn nhất thì \(x\) nhận giá trị nào sau đây?
A.\(x = \frac{{\sqrt {35} }}{7}\)
B.\(x = 1.\)
C.\(x = \frac{9}{4}\)
D. \(x = \frac{{\sqrt {34} }}{7}\)
Đáp án chính xác
Trả lời:
Gọi
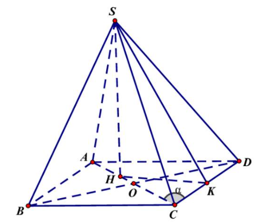
\(H\)là tâm đường tròn ngoại tiếp tam giác \(BCD,\) do \(SB = SC = SD\) nên \(SH\) là trục của đường tròn ngoại tiếp tam giác \(BCD,\) suy ra \(SH \bot \left( {ABCD} \right).\)
Do tứ giác \(ABCD\) là hình thoi nên \(AC\) là đường trung trực của đường thẳng \(BD\) do đó \(H \in AC.\)
Đặt \(\alpha = \widehat {ACD},0 < \alpha < \frac{\pi }{2} \Rightarrow \widehat {BCD} = 2\alpha ,\) suy ra \({S_{ABCD}} = 2{S_{BCD}} = BC.CD.\sin \widehat {BCD} = \sin 2\alpha .\)
Gọi \(K\) là trung điểm của \(CD \Rightarrow CD \bot SK,\) mà \(CD \bot SH\) suy ra \(CD \bot HK.\)
\(HC = \frac{{CK}}{{\cos \alpha }} = \frac{1}{{2\cos \alpha }},SH = \sqrt {S{C^2} – H{C^2}} = \sqrt {1 – \frac{1}{{4{{\cos }^2}\alpha }}} = \frac{{\sqrt {4{{\cos }^2}\alpha – 1} }}{{2\cos \alpha }}\).
Thể tích khối chóp \(S.ABCD\) là \(V = \frac{1}{3}SH.{S_{ABCD}} = \frac{1}{3}\frac{{\sqrt {4\cos \alpha – 1} }}{{2\cos \alpha }}.\sin 2\alpha = \frac{1}{3}\sin \alpha \sqrt {4{{\cos }^2}\alpha – 1} \)
Do đó \(V = \frac{1}{6}\left( {2\sin \alpha } \right)\sqrt {4{{\cos }^2}\alpha – 1} \le \frac{1}{6}\frac{{4{{\sin }^2}\alpha + 4{{\cos }^2}\alpha – 1}}{2} = \frac{1}{4}.\)
Dấu “=” xảy ra khi \(2\sin \alpha = \sqrt {4{{\cos }^2}\alpha – 1} \Leftrightarrow 4{\sin ^2}\alpha = 4{\cos ^2}\alpha – 1 \Leftrightarrow {\cos ^2}\alpha = \frac{5}{8}\)
\( \Leftrightarrow \cos \alpha = \frac{{\sqrt {10} }}{4}.\) Khi đó \(HC = \frac{2}{{\sqrt {10} }},SH = \frac{{\sqrt {15} }}{5}.\)
Gọi \(O = AC \cap BD,\) suy ra \(AC = 2OC = 2CD.\cos \alpha = \frac{{\sqrt {10} }}{2}.\)
\(AH = AC – HC = \frac{{\sqrt {10} }}{2} – \frac{2}{{\sqrt {10} }} = \frac{3}{{\sqrt {10} }}.\)
Vậy \(x = SA = \sqrt {S{H^2} + A{H^2}} = \sqrt {\frac{3}{5} + \frac{9}{{10}}} = \frac{{\sqrt 6 }}{2}.\)
Đáp án D.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong các phương trình dưới đây, phương trình nào có tập nghiệm là: \(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.\)
Câu hỏi:
Trong các phương trình dưới đây, phương trình nào có tập nghiệm là: \(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.\)
A.\(\sin x = 1\)
B.\(\cos x = 0\)
Đáp án chính xác
C.\(\sin x = 0\)
D. \(\cos x = 1\)
Trả lời:
Ta có: \(\sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}.\)
\(\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.\)
\(\sin x = 0 \Leftrightarrow x = k\pi ,k \in \mathbb{Z}.\)
\(\cos x = 1 \Leftrightarrow x = k2\pi ,k \in \mathbb{Z}.\)
Đáp án B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đồ thị hàm số \(y = \frac{{x – 2}}{{x + 4}}\) cắt trục tung tại điểm có tung độ bằng
Câu hỏi:
Đồ thị hàm số \(y = \frac{{x – 2}}{{x + 4}}\) cắt trục tung tại điểm có tung độ bằng
A.0.
B.2.
C.\(\frac{1}{2}.\)
D. \( – \frac{1}{2}.\)
Đáp án chính xác
Trả lời:
Giao điểm của đồ thị hàm số với trục tung. Cho \(x = 0 \Rightarrow y = \frac{{0 – 2}}{{0 + 4}} = \frac{{ – 1}}{2}.\)
Vậy đồ thị hàm số \(y = \frac{{x – 2}}{{x + 4}}\) cắt trục tung tại điểm có tung độ bằng \(\frac{{ – 1}}{2}.\)
Đáp án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình chóp tứ giác có đáy là hình vuông cạnh \(a,\) khi cạnh đáy của hình chóp giảm đi 3 lần và vẫn giữ nguyên chiều cao thì thể tích của khối chóp giảm đi mấy lần:
Câu hỏi:
Cho hình chóp tứ giác có đáy là hình vuông cạnh \(a,\) khi cạnh đáy của hình chóp giảm đi 3 lần và vẫn giữ nguyên chiều cao thì thể tích của khối chóp giảm đi mấy lần:
A.6.
B.9.
Đáp án chính xác
C.27.
D. 3.
Trả lời:
* Thể tích hình chóp tứ giác có đáy là hình vuông cạnh \(a,\) chiều cao \(h\) là: \({V_1} = \frac{1}{3}{a^2}.h\)
* Thể tích hình chóp tứ giác có đáy là hình vuông cạnh \(\frac{a}{3},\) chiều cao \(h\) là: \({V_2} = \frac{1}{3}\frac{{{a^2}}}{9}h.\)
* Tỷ số thể tích là: \(\frac{{{V_1}}}{{{V_2}}} = 9.\)
Đáp án B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Chọn kết quả sai trong các kết quả dưới đây:
Câu hỏi:
Chọn kết quả sai trong các kết quả dưới đây:
A.\(\mathop {\lim }\limits_{x \to {x_0}} x = {x_0}\)
B.\(\mathop {\lim }\limits_{x \to – \infty } {x^5} = – \infty \)
C.\(\mathop {\lim }\limits_{x \to + \infty } \frac{2}{{{x^2}}} = + \infty \)
Đáp án chính xác
D. \(\mathop {\lim }\limits_{x \to {1^ + }} c = c\)
Trả lời:
Ta có:
\(\mathop {\lim }\limits_{x \to {x_0}} x = {x_0}\)
\(\mathop {\lim }\limits_{x \to – \infty } {x^5} = – \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \frac{2}{{{x^2}}} = 0\)
\(\mathop {\lim }\limits_{x \to {1^ + }} c = c.\)
Đáp án C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hàm số \(y = \sqrt {2x – {x^2}} \) nghịch biến trên khoảng:
Câu hỏi:
Hàm số \(y = \sqrt {2x – {x^2}} \) nghịch biến trên khoảng:
A.\(\left( {0;1} \right)\)
B.\(\left( {1; + \infty } \right)\)
C.\(\left( {0;2} \right)\)
D. \(\left( {1;2} \right)\)
Đáp án chính xác
Trả lời:
Tập xác định \(D = \left[ {0;2} \right].\)
Ta có \(y’ = \frac{{1 – x}}{{\sqrt {2x – {x^2}} }},\forall x \in \left( {0;2} \right).\)
\(y’ = 0 \Leftrightarrow x = 1.\)
Bảng biến thiên
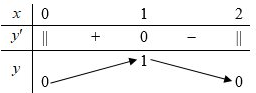
Dựa vào bảng biến thiên, ta thấy hàm số nghịch biến trên khoảng \(\left( {1;2} \right).\)
Đáp án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====