Câu hỏi:
Nhà bạn Minh cần khoan một cái giếng nước. Biết rằng giá tiền của mét khoan đầu tiên là 200.000đ và kể từ mét khoan thứ hai, giá tiền của mỗi mét sau tăng thêm 7% so với giá tiền của mét khoan ngay trước nó. Hỏi nếu nhà bạn An khoan cái giếng sâu 30m thì hết bao nhiêu tiền (làm tròn đến hàng nghìn)?
A. \(18895000\)đ.
B. \(1422851\)đ.
C. \(18892000\)đ.
Đáp án chính xác
D. \(18892200\)đ.
Trả lời:
Bài toán tổng quát:
Giả sử giá tiền của mét khoan đầu tiên là \(x\) (đồng) và giá tiền của mỗi mét sau tăng thêm \(y\% \) so với giá tiền của mét khoan ngay trước đó \(\left( {x >0;y >0} \right).\) Ta có:
* Giá tiền mét khoan đầu tiên là \({S_1} = x\) (đồng)
* Giá tiền mét khoan thứ hai là \({S_2} = x + \frac{y}{{100}}.x = \frac{{y + 100}}{{100}}.x\) (đồng)
* Giá tiền mét khoan thứ ba là \({S_3} = {S_2} + \frac{y}{{100}}.{S_2} = \frac{{y + 100}}{{100}}.{S_2} = {\left( {\frac{{y + 100}}{{100}}} \right)^2}.x\) (đồng)
* Giá tiền của mét khoan thứ ba là \({S_4} = {S_3} + \frac{y}{{100}}.{S_3} = \frac{{y + 100}}{{100}}.{S_3} = {\left( {\frac{{y + 100}}{{100}}} \right)^3}.x\) (đồng)
…………………………………………………………………………………………
* Giá tiền của mét khoan thứ \(n\) là \({S_n} = {S_{n – 1}} + \frac{y}{{100}}.{S_{n – 1}} = \frac{{y + 100}}{{100}}.{S_{n – 1}} = {\left( {\frac{{y + 100}}{{100}}} \right)^{n – 1}}.x\) (đồng)
\( \Rightarrow \) Giá tiền để khoan cái giếng sâu \(n\) mét là:
\(S = {S_1} + {S_2} + {S_3} + … + {S_n} = \left[ {1 + \frac{{y + 100}}{{100}} + {{\left( {\frac{{y + 100}}{{100}}} \right)}^2} + … + {{\left( {\frac{{y + 100}}{{100}}} \right)}^{n – 1}}} \right].x\)
Đặt \(k = \frac{{y + 100}}{{100}} \Rightarrow S = \left( {1 + k + {k^2} + … + {k^{n – 1}}} \right).x = \frac{{x\left( {1 – {k^n}} \right)}}{{1 – k}}\)
\(k = 1,07\) và \({S_{30}} = \frac{{200000.\left( {1 – {{1.07}^{30}}} \right)}}{{1 – 1,07}} \approx 18892000\) (đồng)
Vậy nếu nhà bạn An khoan cái giếng sâu 30 m thì hết 18892000 đồng.
Đáp án C
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đồ thị của hàm số nào dưới đây có dạng đường cong trong hình vẽ sau?
Câu hỏi:
Đồ thị của hàm số nào dưới đây có dạng đường cong trong hình vẽ sau?
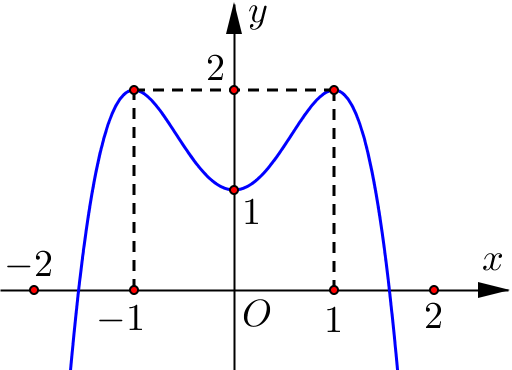
A. \(y = 2{x^4} – {x^2} + 1\).
Đáp án chính xác
B. \(y = – {x^4} + {x^2} + 1\).
C. \(y = – {x^4} + 2{x^2} + 1\).
D. \(y = {x^4} – 2{x^2} + 1\).
Trả lời:
Dựa vào đồ thị ta có đồ thị trên là đồ thị hàm bậc bốn trùng phương có bề lõm hướng xuống nên hệ số \(a < 0\) nên loại đáp án A và D.
Xét điểm \(\left( {1;2} \right)\) thuộc đồ thị hàm số trên.
Thay \(\left( {1;2} \right)\) vào \(y = – {x^4} + {x^2} + 1\) ta được 2 =1 (vô lý).
Thay \(\left( {1;2} \right)\) vào \(y = – {x^4} + 2{x^2} + 1\) ta được 2 = 2 (đúng).
Nên đồ thị trong hình vẽ trên là đồ thị của hàm số \(y = – {x^4} + 2{x^2} + 1.\)
Đáp án A====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số nghiệm của phương trình\(\frac{{\sin 2x}}{{\cos x + 1}} = 0\) trên đoạn \(\left[ {0;2020\pi } \right]\) là
Câu hỏi:
Số nghiệm của phương trình\(\frac{{\sin 2x}}{{\cos x + 1}} = 0\) trên đoạn \(\left[ {0;2020\pi } \right]\) là
A. \(3030\)
B. 2020
C. 3031
Đáp án chính xác
D. 4040
Trả lời:
Điều kiện: \(\cos x + 1 \ne 0 \Leftrightarrow x \ne \pi + l2\pi \left( {l \in \mathbb{Z}} \right)\).
Ta có:
\(\frac{{\sin 2x}}{{\cos x + 1}} = 0 \Leftrightarrow \sin 2x = 0 \Leftrightarrow 2x = k\pi \left( {k \in \mathbb{Z}} \right) \Leftrightarrow x = k\frac{\pi }{2}\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + m\pi \left( {m \in \mathbb{Z}} \right)\\x = n2\pi \left( {n \in \mathbb{Z}} \right)\\x = \pi + p2\pi \left( {p \in \mathbb{Z}} \right)\end{array} \right.\)
So lại với điều kiện, phương trình có họ nghiệm là \(\left[ \begin{array}{l}x = \frac{\pi }{2} + m\pi \left( {m \in \mathbb{Z}} \right)\\x = n2\pi \left( {n \in \mathbb{Z}} \right)\end{array} \right..\)
Xét \(0 \le \frac{\pi }{2} + m\pi \le 2020\pi \Leftrightarrow – \frac{\pi }{2} \le m\pi \le \frac{{4039}}{2}\pi \Leftrightarrow – \frac{1}{2} \le m \le \frac{{4039}}{2}.\) Vì \(m \in \mathbb{Z}\) nên có 2002 giá trị \(m\) thỏa mãn đề bài.
Xét \(0 \le n2\pi \le 2020\pi \Leftrightarrow 0 \le n\pi \le 1010.\) Vì \(n \in \mathbb{Z}\) nên có 1011 giá trị \(n\) thỏa mãn đề bài.
Vậy phương trình có tổng cộng 3031 nghiệm trên đoạn \(\left[ {0;2020\pi } \right].\)
Đáp án C====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số nghiệm của phương trình \({\log _4}\left( {3{x^2} + x} \right) = \frac{1}{2}\) là
Câu hỏi:
Số nghiệm của phương trình \({\log _4}\left( {3{x^2} + x} \right) = \frac{1}{2}\) là
A. \(1\).
B. \(5\).
C. \(0\).
D. \(2\).
Đáp án chính xác
Trả lời:
Ta có \({\log _4}\left( {3{x^2} + x} \right) = \frac{1}{2} \Leftrightarrow 3{x^2} + x = 2\)
\( \Leftrightarrow 3{x^2} + x – 2 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = – 1\\x = – \frac{2}{3}\end{array} \right..\)
Vậy phương trình có hai nghiệm.
Đáp án D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Với \(a\) là số thực dương khác \(1\) tùy ý, \({\log _{{a^5}}}{a^4}\) bằng
Câu hỏi:
Với \(a\) là số thực dương khác \(1\) tùy ý, \({\log _{{a^5}}}{a^4}\) bằng
A. \(\frac{1}{5}\).
B. \(\frac{4}{5}\).
Đáp án chính xác
C. \(20\).
D. \(\frac{5}{4}\).
Trả lời:
Ta có \({\log _{{a^5}}}{a^4} = \frac{4}{5}{\log _a}a = \frac{4}{5}.\)
Đáp án B====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Khối chóp có một nửa diện tích đáy là \(S\), chiều cao là \(2h\) thì có thể tích là:
Câu hỏi:
Khối chóp có một nửa diện tích đáy là \(S\), chiều cao là \(2h\) thì có thể tích là:
A. \(V = \frac{1}{2}S.h\).
B. \(V = \frac{1}{3}S.h\).
C. \(V = S.h\).
D. \(V = \frac{4}{3}S.h\).
Đáp án chính xác
Trả lời:
Áp dụng công thức thể tích khối chóp ta có: \(V = \frac{1}{3}.2S.2h = \frac{4}{3}S.h\)
Vậy chọn đáp án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====