Câu hỏi:
Bài 4 trang 91 sách bài tập Toán lớp 6 Tập 2: Cho ba điểm phân biệt không thẳng hàng. Em hãy vẽ một đường thẳng đi qua hai trong số ba điểm đó, rồi vẽ tiếp đường thẳng thứ hai đi qua điểm còn lại và song song với đường thẳng vừa vẽ.
Trả lời:
Lời giải:
Giả sử ba điểm phân biệt không thẳng hàng là A, B, C.
Cách vẽ:
– Lấy ba điểm A, B, C không thẳng hàng.
– Vẽ đường thẳng d đi qua B, C.
– Vẽ đường thẳng đi qua A và song song với đường thẳng BC bằng eke.
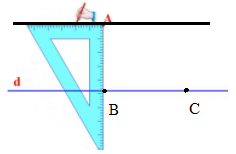
Ta có hình vẽ sau:

====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Lý thuyết Hai đường thẳng cắt nhau, song song. Tia (Chân trời sáng tạo 2023) hay, chi tiết | Toán lớp 6
Lý thuyết Toán lớp 6 Bài 3: Hai đường thẳng cắt nhau, song song. Tia
Video giải Toán 6 Bài 3: Hai đường thẳng cắt nhau, song song. Tia – Chân trời sáng tạo
A. Lý thuyết Hai đường thẳng cắt nhau, song song. Tia
1. Hai đường thẳng cắt nhau, song song
– Nếu hai đường thẳng chỉ có một điểm chung, ta nói rằng hai đường thẳng đó cắt nhau. Điểm chung được gọi là giao điểm của hai đường thẳng.
Ví dụ 1. Hai đường thẳng a và b chỉ có một điểm chung là M, ta nói rằng hai đường thẳng a và b cắt nhau (như hình vẽ).
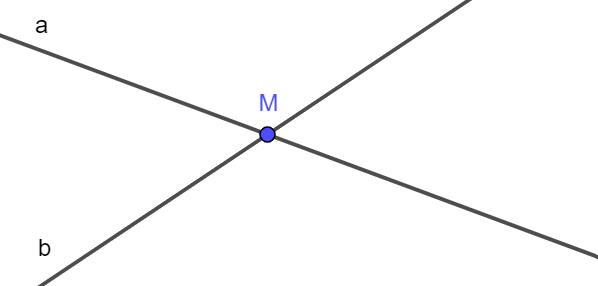
Khi đó, M là giao điểm của hai đường thẳng a và b.
– Nếu hai đường thẳng không có điểm chung nào, ta nói rằng hai đường thẳng đó song song với nhau.
Ví dụ 2. Hai đường thẳng c và d không có điểm chung nào (như hình vẽ).
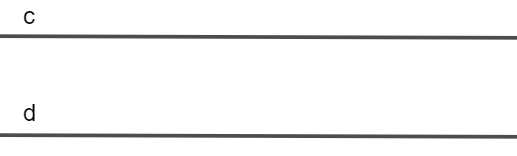
Khi đó, ta nói hai đường thẳng a và b song song với nhau.
Chú ý: Từ nay về sau, khi nói hai đường thẳng mà không nói gì thêm, ta hiểu đó là hai đường thẳng phân biệt.
2. Tia
Mỗi điểm O trên một đường thẳng chia đường thẳng đó thành hai phần, mỗi phần gọi là một tia gốc O.
Chú ý:
– Từ một điểm O kẻ một vạch thẳng về một phía của điểm O để biểu diễn một tia gốc O.
– Nếu A là một điểm tùy ý trên tia Ox, ta có thể gọi tia Ox là tia OA (như hình vẽ).

– Khi viết (đọc) tia, ta phải viết (đọc) gốc của tia trước.
Ví dụ 3. Cho hình vẽ.

Trong hình vẽ có O là điểm gốc.
Ta viết (đọc) gốc của tia trước, viết (đọc) là: tia Ox.
B. Bài tập tự luyện
Bài 1. Cho đường thẳng AB bất kỳ. Hãy vẽ hình trong các trường hợp sau:
a) Đường thẳng GH cắt đường thẳng AB;
b) Đường thẳng IK song song với đường thẳng AB.
Lời giải:
a) Đường thẳng GH cắt đường thẳng AB nên hai đường thẳng này có một điểm chung.
Chẳng hạn: vẽ hai đường thẳng GH và AB cắt nhau tại điểm M.
Cách vẽ:
Bước 1: Vẽ đường thẳng AB bất kỳ.

Bước 2: Lấy điểm M bất kỳ thuộc đường thẳng AB, giả sử điểm M nằm giữa hai điểm A và B.

Bước 3: Vẽ đường thẳng đi qua M và không trùng với đường thẳng AB.
Ta có đường thẳng GH cắt đường thẳng AB như hình vẽ:

b) Cách vẽ đường thẳng IK song song với đường thẳng AB:
Bước 1: Vẽ đường thẳng AB bất kỳ.

Bước 2: Lấy điểm I nằm ngoài đường thẳng AB.

Bước 3: Vẽ đường thẳng đi qua điểm I và song song với đường thẳng AB. Lấy điểm K thuộc đường thẳng vừa vẽ.
Ta được đường thẳng IK song song với đường thẳng AB như hình vẽ:

Bài 2. Đếm số giao điểm tạo bởi bốn đường thẳng trong mỗi hình sau:
a)

b)

c)

Lời giải:
a) Trong hình a) có ba đường thẳng song song với nhau nên không có giao điểm nào.
b) Đặt các đường thẳng trong hình b) là các đường thẳng a, b, c, d.
Giả sử bốn đường thẳng a, b, c, d cắt nhau tại điểm M (như hình vẽ).

Vậy trong hình b) có một giao điểm tạo bởi bốn đường thẳng.
c) Đặt các đường thẳng trong hình c) là các đường thẳng m, n, p, q.
Giả sử đường thẳng m và p cắt nhau tại điểm A, đường thẳng n và p cắt nhau tại điểm B, đường thẳng m và q cắt nhau tại C, đường thẳng n và q cắt nhau tại D (như hình vẽ).

Do đó bốn đường thẳng m, n, p, q đôi một cắt nhau tại các điểm A, B, C, D.
Vậy trong hình c) có bốn giao điểm tạo bởi bốn đường thẳng.
Bài 3. Cho hai đường thẳng XY và EF cắt nhau tại điểm O. Kể tên các tia có gốc O.
Lời giải:
Cách vẽ:
– Vẽ đường thẳng XY bất kỳ.
– Lấy điểm O thuộc đường thẳng XY.
– Vẽ đường thẳng EF đi qua O (đường thẳng EF không trùng với đường thẳng XY).
Ta có hình vẽ:

Hai đường thẳng XY và EF cắt nhau tại điểm O nên điểm O nằm trên hai đường thẳng này.
– Điểm O nằm trên đường thẳng XY nên điểm O chia đường thẳng XY thành hai tia có chung gốc O là tia OX, OY.
– Điểm O nằm trên đường thẳng EF nên điểm O chia đường thẳng EF thành hai tia có chung gốc O là tia OE, OF.
Vậy các tia có gốc O là: OX, OY, OE, OF.
Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 2: Ba điểm thẳng hàng. Ba điểm không thẳng
Lý thuyết Bài 3: Hai đường thẳng cắt nhau, song song. Tia
Lý thuyết Bài 4: Đoạn thẳng. Độ dài đoạn thẳng
Lý thuyết Bài 5: Trung điểm của đoạn thẳng
Lý thuyết Bài 6: Góc
- Sách bài tập Toán 6 Bài 3 (Chân trời sáng tạo): Hai đường thẳng cắt nhau, song song. Tia
Giải SBT Toán lớp 6 Bài 3: Hai đường thẳng cắt nhau, song song. Tia
Bài 1 trang 91 sách bài tập Toán lớp 6 Tập 2: Qua hai điểm A và B cho trước có bao nhiêu đường thẳng? Em hãy chọn phương án đúng.
(A) 1.
(B) 2.
(C) Nhiều hơn 2.
(D) Không có đường thẳng nào.
Lời giải:
Qua hai điểm A và B cho trước có duy nhất một đường thẳng.
Vậy phương án đúng là A.
Bài 2 trang 91 sách bài tập Toán lớp 6 Tập 2: Vì sao người ta thường nói “đường thẳng đi qua hai điểm” mà không nói “đường thẳng đi qua 3 điểm”.
Lời giải:
Người ta thường nói “đường thẳng đi qua hai điểm” mà không nói “đường thẳng đi qua 3 điểm” vì:
– Qua hai điểm phân biệt cho trước luôn xác định duy nhất một đường thẳng.
– Qua ba điểm cho trước không phải lúc nào cũng xác định được một đường thẳng (chỉ xác định được đường thẳng khi ba điểm đó thẳng hàng).
Bài 3 trang 91 sách bài tập Toán lớp 6 Tập 2: Điền các chữ “cắt nhau”, “song song” vào chỗ chấm thích hợp.
a) Hai đường thẳng không có điểm chung nào gọi là hai đường thẳng ……..
b) Hai đường thẳng có duy nhất một điểm chung gọi là hai đường thẳng…..
Lời giải:
a) Hai đường thẳng không có điểm chung nào gọi là hai đường thẳng song song.
b) Hai đường thẳng có duy nhất một điểm chung gọi là hai đường thẳng cắt nhau.
Bài 4 trang 91 sách bài tập Toán lớp 6 Tập 2: Cho ba điểm phân biệt không thẳng hàng. Em hãy vẽ một đường thẳng đi qua hai trong số ba điểm đó, rồi vẽ tiếp đường thẳng thứ hai đi qua điểm còn lại và song song với đường thẳng vừa vẽ.
Lời giải:
Giả sử ba điểm phân biệt không thẳng hàng là A, B, C.
Cách vẽ:
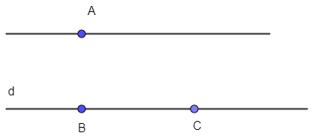
– Lấy ba điểm A, B, C không thẳng hàng.
– Vẽ đường thẳng d đi qua B, C.
– Vẽ đường thẳng đi qua A và song song với đường thẳng BC bằng eke.
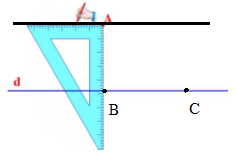
Ta có hình vẽ sau:
Bài 5 trang 91 sách bài tập Toán lớp 6 Tập 2: Cho bốn đường thẳng a, b, c, d trong đó có ba đường thẳng a, b, c cắt nhau tại một điểm. Các đường thẳng b, c, d cắt nhau tại một điểm. Bốn đường thẳng a, b, c, d có cắt nhau tại một điểm hay không? Vì sao?
Lời giải:
Bốn đường thẳng a, b, c, d cắt nhau tại một điểm.
Vì giả sử ba đường thẳng a, b, c cắt nhau tại điểm A. Ta có hai đường thẳng b, c cắt nhau duy nhất tại điểm A.
Mà đường thẳng d cắt đường thẳng b và đường thẳng c tại một điểm. Nên đường thẳng d cắt đường thẳng b, c tại điểm A.
Khi đó, bốn đường thẳng a, b, c, d cùng cắt nhau tại điểm A.

Bài 6 trang 91 sách bài tập Toán lớp 6 Tập 2: Hãy vẽ ba đường thẳng sao cho cứ hai trong số ba đường thẳng đó đều cắt nhau. Ký hiệu các giao điểm của các đường thẳng đó. Có bao nhiêu giao điểm được tạo thành?
Lời giải:
Vẽ hai đường thẳng cắt nhau tại A, ta có ba trường hợp sau:
– Trường hợp 1: Đường thẳng thứ ba cắt cả hai đường thẳng kia và đi qua giao điểm A thì ta có một giao điểm A (như hình vẽ).
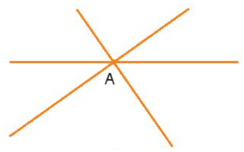
– Trường hợp 2: Đường thẳng thứ ba cắt cả hai đường thẳng kia và không đi qua giao điểm A thì ta có ba giao điểm A, B và C (như hình vẽ).
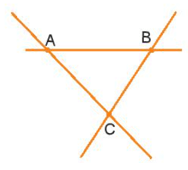
Bài 7 trang 91 sách bài tập Toán lớp 6 Tập 2: Có bao nhiêu giao điểm được tạo bởi ba đường thẳng? Hãy vẽ hình trong mỗi trường hợp đó.
Lời giải:
Vẽ hai đường thẳng trước, có hai khả năng xảy ra:
* Khả năng 1: Hai đường thẳng đó song song với nhau.
Ta tiếp tục vẽ thêm một đường thẳng thứ ba song song hoặc cắt cả hai đường thẳng kia.
– Trường hợp 1: Đường thẳng thứ ba song song cả hai đường thẳng kia thì ba đường thẳng này không có giao điểm nào (như hình vẽ).

– Trường hợp 2: Đường thẳng thứ ba cắt cả hai đường thẳng kia thì ta có hai giao điểm A và B (như hình vẽ).
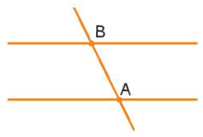
* Khả năng 2: Hai đường thẳng đó cắt nhau cắt nhau tại điểm A.
Ta tiếp tục vẽ thêm một đường thẳng thứ ba cắt cả hai đường thẳng kia.
– Trường hợp 1: Đường thẳng thứ ba cắt cả hai đường thẳng kia và đi qua giao điểm A thì ta có một giao điểm A (như hình vẽ).

– Trường hợp 2: Đường thẳng thứ ba cắt cả hai đường thẳng kia và không đi qua giao điểm A thì ta có ba giao điểm A, B và C (như hình vẽ).

Bài 8 trang 91 sách bài tập Toán lớp 6 Tập 2: Cho bốn điểm A, B, C, D như hình vẽ bên. Có bao nhiêu tia được tạo thành nếu mỗi tia đều chứa hai trong số các điểm đó?
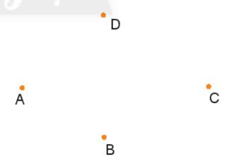
Lời giải:
– Chọn điểm A làm điểm gốc thì có thể vẽ được 3 tia AB, AC và AD.
– Chọn điểm B làm điểm gốc thì có thể vẽ được 3 tia BA, BC và BD.
– Chọn điểm C làm điểm gốc thì có thể vẽ được 3 tia CA, CB và CD.
– Chọn điểm D làm điểm gốc thì có thể vẽ được 3 tia DA, DB và DC.
Vậy từ bốn điểm A, B, C, D có 12 tia được tạo thành (mỗi tia chứa hai trong số các điểm đó) là: AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB, DC.
Bài 9 trang 91 sách bài tập Toán lớp 6 Tập 2: Hai đường thẳng cắt nhau tạo ra mấy tia? Hãy đặt tên cho các tia đó.
Lời giải:
Gọi hai đường thẳng lần lượt là xy và mn, hai đường thẳng này cắt nhau tại điểm O (như hình vẽ).
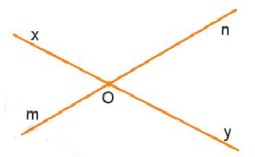
Điểm O chia đường thẳng xy thành hai phần là tia Ox và tia Oy, đường thẳng mn thành hai phần là tia Om và tia On.
Vậy bốn tia được tạo thành là: Ox, Oy, Om, On.
Bài 10 trang 91 sách bài tập Toán lớp 6 Tập 2: Hãy vẽ hình tương ứng trong mỗi trường hợp sau:
a) Tia MN;
b) Tia NM;
c) Đường thẳng MN.
Lời giải:
a) Cách vẽ tia MN:
– Lấy hai điểm M và N bất kỳ.
– Cho điểm M làm điểm gốc.
– Nối M với N và kéo dài qua điểm N, ta được tia MN.
Ta có hình vẽ sau:

b) Cách vẽ tia NM:
– Lấy hai điểm M và N bất kỳ.
– Cho điểm N làm điểm gốc.
– Nối N với M và kéo dài qua điểm M, ta được tia NM.
Ta có hình vẽ sau:

c) Cách vẽ đường thẳng MN:
– Lấy hai điểm M và N bất kỳ.
– Nối M với N và kéo dài về cả hai phía, ta được đường thẳng MN.
Ta có hình vẽ sau:

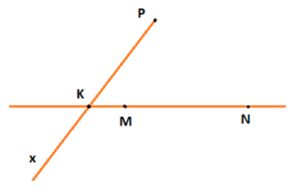
Bài 11 trang 91 sách bài tập Toán lớp 6 Tập 2: Cho điểm P không nằm trên đường thẳng MN. Vẽ tia Px cắt đường thẳng MN tại điểm K sao cho điểm M nằm giữa K và N.
Lời giải:
Cách vẽ:
Bước 1: Vẽ đường thẳng MN và điểm P nằm ngoài đường thẳng đó.
Bước 2: Lấy điểm K nằm trên đường thẳng MN sao cho K không nằm giữa M và N.
Bước 3: Nối P với K và kéo dài qua điểm K, kí hiệu tia Px.
Ta hình vẽ như sau:
- Bài 1 trang 91 sách bài tập Toán lớp 6 Tập 2: Qua hai điểm A và B cho trước có bao nhiêu đường thẳng? Em hãy chọn phương án đúng.
(A) 1.
(B) 2.
(C) Nhiều hơn 2.
(D) Không có đường thẳng nào.
Câu hỏi:
Bài 1 trang 91 sách bài tập Toán lớp 6 Tập 2: Qua hai điểm A và B cho trước có bao nhiêu đường thẳng? Em hãy chọn phương án đúng.
(A) 1.
(B) 2.
(C) Nhiều hơn 2.
(D) Không có đường thẳng nào.Trả lời:
Lời giải:
Qua hai điểm A và B cho trước có duy nhất một đường thẳng.
Vậy phương án đúng là A.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Bài 2 trang 91 sách bài tập Toán lớp 6 Tập 2: Vì sao người ta thường nói “đường thẳng đi qua hai điểm” mà không nói “đường thẳng đi qua 3 điểm”.
Câu hỏi:
Bài 2 trang 91 sách bài tập Toán lớp 6 Tập 2: Vì sao người ta thường nói “đường thẳng đi qua hai điểm” mà không nói “đường thẳng đi qua 3 điểm”.
Trả lời:
Lời giải:
Người ta thường nói “đường thẳng đi qua hai điểm” mà không nói “đường thẳng đi qua 3 điểm” vì:
– Qua hai điểm phân biệt cho trước luôn xác định duy nhất một đường thẳng.
– Qua ba điểm cho trước không phải lúc nào cũng xác định được một đường thẳng (chỉ xác định được đường thẳng khi ba điểm đó thẳng hàng).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Bài 3 trang 91 sách bài tập Toán lớp 6 Tập 2: Điền các chữ “cắt nhau”, “song song” vào chỗ chấm thích hợp.
a) Hai đường thẳng không có điểm chung nào gọi là hai đường thẳng ……..
b) Hai đường thẳng có duy nhất một điểm chung gọi là hai đường thẳng…..
Câu hỏi:
Bài 3 trang 91 sách bài tập Toán lớp 6 Tập 2: Điền các chữ “cắt nhau”, “song song” vào chỗ chấm thích hợp.
a) Hai đường thẳng không có điểm chung nào gọi là hai đường thẳng ……..
b) Hai đường thẳng có duy nhất một điểm chung gọi là hai đường thẳng…..Trả lời:
Lời giải:
a) Hai đường thẳng không có điểm chung nào gọi là hai đường thẳng song song.
b) Hai đường thẳng có duy nhất một điểm chung gọi là hai đường thẳng cắt nhau.====== **** mời các bạn xem câu tiếp bên dưới **** =====