Câu hỏi:
Cho số sau: \(\overline {x45y} \). Tìm giá trị lớn nhất của tổng hai chữ số x và y sao cho \(\overline {x45y} \) vừa chia hết cho 5 vừa chia hết cho 3?
A. 10;
B. 15;
C. 9;
D. 12.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
Số \(\overline {x45y} \) có chữ số tận cùng là y. Để \(\overline {x45y} \) chia hết cho 5 thì y phải là 0 hoặc 5.
Trường hợp 1: y = 0 ta có số \(\overline {x450} \), tổng các chữ số trong đó là x + 4 + 5 + 0 = 9 + x. Để \(\overline {x450} \) chia hết cho 3 thì 9 + x phải chia hết cho 3. Vì x là chữ số đầu tiên nên \(0 < x \le 9,x \in N\), do đó x có thể là 3; 6; 9.
Trường hợp 2: y = 5 ta có số \(\overline {x455} \), tổng các chữ số trong đó là x + 4 + 5 + 5 = 14 + x. Để \(\overline {x455} \) chia hết cho 3 thì 14 + x phải chia hết cho 3. Vì x là chữ số đầu tiên nên \(0 < x \le 9,x \in N\), do đó x có thể là 1; 4; 7.
Suy ra các cặp chữ số (x, y) thỏa mãn là: (3; 0); (6; 0); (9; 0); (1; 5); (4; 5); (7; 5).
Vậy tổng x + y lớn nhất thỏa mãn là 7 + 5 = 12.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Lý thuyết Dấu hiệu chia hết cho 3, cho 9 (Cánh diều 2023) hay, chi tiết | Toán lớp 6
Lý thuyết Toán lớp 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9
Video giải Toán 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9 – Cánh diều
A. Lý thuyết Dấu hiệu chia hết cho 3, cho 9
I. Dấu hiệu chia hết cho 3
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
Ví dụ:
+ Số 102 có tổng các chữ số là 1 + 0 + 2 = 3 chia hết cho 3 thì số 102 chia hết cho 3.
+ Số 321 có tổng các chữ số là 3 + 2 + 1 = 6 chia hết cho 3 thì số 321 chia hết cho 3.
II. Dấu hiệu chia hết cho 9
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
Ví dụ:
+ Số 792 có tổng các chữ số là 7 + 9 + 2 = 18 chia hết cho 9 thì số 792 chia hết cho 9.
+ Số 108 có tổng các chữ số là 1 + 0 + 8 = 9 chia hết cho 9 thì số 108 chia hết cho 9.
B. Bài tập tự luyện
Bài 1. Cho các số 104, 627, 3 114, 5 123, 6 831 và 72 102. Trong các số đó:
a) Số nào chia hết cho 3? Vì sao?
b) Số nào không chia hết cho 3? Vì sao?
c) Số nào chia hết cho 9? Vì sao?
d) Số nào chia hết cho 3, nhưng không chia hết cho 9? Vì sao?
Lời giải:
Ta áp dụng dấu hiệu chia hết cho 3 và dấu hiệu chia hết cho 9 để thực hiện bài tập này.
a) Trong các số đã cho ta có:
+ Số 627 chia hết cho 3 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3.
+ Số 3 114 chia hết cho 3 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 3.
+ Số 6 831 chia hết cho 3 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 3.
+ Số 72 102 chia hết cho 3 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3.
b) Ta có:
+ Số 104 không chia hết cho 3 vì tổng các chữ số 1 + 0 + 4 = 5 không chia hết cho 3.
+ Số 5 123 không chia hết cho 3 vì tổng các chữ số 5 + 1 + 2 + 3 = 11 không chia hết cho 3.
c) Ta có:
+ Số 3 114 chia hết cho 9 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 9.
+ Số 6 831 chia hết cho 9 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 9.
d) Ta có:
+ Số 627 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3 nhưng không chia hết cho 9.
+ Số 72 102 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3 nhưng không chia hết cho 9.
Bài 2. Chứng minh rằng tích của 3 số tự nhiên liên tiếp luôn chia hết cho 3.
Lời giải:
Gọi 3 số tự nhiên liên tiếp là n; n + 1; n + 2 (với
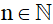)Tích của ba số tự nhiên liên tiếp là n(n + 1)(n + 2)
Mọi số tự nhiên n khi chia cho 3 có thể nhận số dư là 0, 1, 2.
+ Nếu r = 0 thì n chia hết cho 3. Khi đó n(n + 1)(n + 2) chia hết cho 3.
+ Nếu r = 1 thì n có dạng n = 3k + 1 (
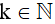)Ta có: n + 2 = 3k + 1 + 2 = 3k + 3 = 3(k + 1) chia hết cho 3.
Do đó: n(n + 1)(n + 2) chia hết cho 3.
+ Nếu r = 2 thì n có dạng n = 3k + 2 (
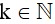)Khi đó: n + 1 = 3k + 2 + 1 = 3(k + 1) chia hết cho 3.
Do đó: n(n + 1)(n + 2) chia hết cho 3.
Vậy tích của ba số tự nhiên liên tiếp chia hết cho 3.
Xem thêm các bài tóm tắt lý thuyết Toán 6 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 8: Dấu hiệu chia hết cho 2, cho 5
Lý thuyết Bài 9: Dấu hiệu chia hết cho 3, cho 9
Lý thuyết Bài 10: Số nguyên tố. Hợp số
Lý thuyết Bài 11: Phân tích một số ra thừa số nguyên tố
Lý thuyết Bài 12: Ước chung và ước chung lớn nhất
- Sách bài tập Toán 6 Bài 9 (Cánh diều): Dấu hiệu chia hết cho 3, cho 9
Giải SBT Toán lớp 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9
Bài 77 trang 27 sách bài tập Toán lớp 6 Tập 1: Cho các số 27; 45; 881; 916; 2 100; 2 439; 13 118; 35 550; 5 223 411. Trong các số đó:
a) Số nào chia hết cho 3?
b) Số nào lớn hơn 2 000 không chia hết cho 3?
c) Số nào chia hết cho 9?
d) Số nào nhỏ hơn 3 000 không chia hết cho 9?
Lời giải:
a) Ta có: 2 + 7 = 9 chia hết cho 3 nên 27 chia hết cho 3;
Ta có: 4 + 5 = 9 chia hết cho 3 nên 45 chia hết cho 3;
Ta có: 8 + 8 + 1 = 17 không chia hết cho 3 nên 881 không chia hết cho 3;
Ta có: 9 + 1 + 6 = 16 không chia hết cho 3 nên 916 không chia hết cho 3;
Ta có: 2 + 1 + 0 + 0 = 3 chia hết cho 3 nên 2 100 chia hết cho 3;
Ta có: 2 + 4 + 3 + 9 = 18 chia hết cho 3 nên 2 439 chia hết cho 3;
Ta có: 1 + 3 + 1 + 1 + 8 = 14 không chia hết cho 3 nên 13 118 không chia hết cho 3;
Ta có: 3 + 5 + 5 + 5 + 0 = 18 chia hết cho 3 nên 35 550 chia hết cho 3;
Ta có: 5 + 2 + 2 + 3 + 4 + 1 + 1 = 18 chia hết cho 3 nên 5 223 411 chia hết cho 3;
Vậy các số chia hết cho 3 là: 27; 45; 2 100; 2 439; 35 550; 5 223 411.
b) Các số còn lại là các số không chia hết cho 3 là: 881; 916; 13 118.
Trong các số này số lớn hơn 2 000 và không chia hết cho 3 là: 13 118.
Vậy số lớn hơn 2 000 và không chia hết cho 3 là: 13 118.
c) Ta có: 2 + 7 = 9 chia hết cho 9 nên 27 chia hết cho 9;
Ta có: 4 + 5 = 9 chia hết cho 9 nên 45 chia hết cho 9;
Ta có: 8 + 8 + 1 = 17 không chia hết cho 9 nên 881 không chia hết cho 9;
Ta có: 9 + 1 + 6 = 16 không chia hết cho 9 nên 916 không chia hết cho 9;
Ta có: 2 + 1 + 0 + 0 = 3 không chia hết cho 9 nên 2 100 không chia hết cho 9;
Ta có: 2 + 4 + 3 + 9 = 18 chia hết cho 9 nên 2 439 chia hết cho 9;
Ta có: 1 + 3 + 1 + 1 + 8 = 14 không chia hết cho 9 nên 13 118 không chia hết cho 9;
Ta có: 3 + 5 + 5 + 5 + 0 = 18 chia hết cho 9 nên 35 550 chia hết cho 9;
Ta có: 5 + 2 + 2 + 3 + 4 + 1 + 1 = 18 chia hết cho 9 nên 5 223 411 chia hết cho 9;
Vậy các số chia hết cho 9 là: 27; 45; 2 439; 35 550; 5 223 411.
d) Các số không chia hết cho 9 mà nhỏ hơn 3 000 là: 881; 916; 2 100.
Bài 78 trang 27 sách bài tập Toán lớp 6 Tập 1: Tìm chữ số x để số
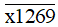thỏa mãn mỗi điều kiện sau:a) Chia hết cho 3;
b) Chia hết cho 9;
c) Chia hết cho 3, nhưng không chia hết cho 9.
Lời giải:
Ta có x + 1 + 2 + 6 + 9 = x + 18.
a) Để số đã cho chia hết cho 3 thì x + 18 chia hết cho 3.
Khi đó x ∈ {0;3;6;9;12…}.
Mà x là chữ số và x khác 0 nên x ∈ {3;6;9}.
Vậy x ∈ {3;6;9}.
b) Để số đã cho chia hết cho 9 thì x + 18 chia hết cho 9.
Khi đó x ∈ {0;9;18;…}.
Mà x là chữ số và x khác 0 nên x = 9.
Vậy x = 9.
c) Để số đã cho chia hết cho 3, nhưng không chia hết cho 9 thì x + 18 chia hết cho 3, nhưng không chia hết cho 9.
Khi đó x ∈ {3;6;12;15…}.
Mà x là chữ số nên x ∈ {3;6}.
Vậy x ∈ {3;6}.
Bài 79 trang 27 sách bài tập Toán lớp 6 Tập 1: Có bao nhiêu số có dạng
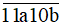chia cho 5 dư 1 và chia hết cho 9?Lời giải:
Để số
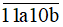chia cho 5 dư 1 thì b ∈ {1;6}.TH1: b = 1
Ta có: 1 + 1 + a + 1 + 0 + 1 = a + 4
Để số
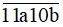chia hết cho 9 thì a + 4 chia hết cho 9 mà a là chữ số nên a = 5.Suy ra 115 101 thỏa mãn chia 5 dư 1 và chia hết cho 9.
TH2: b = 6
Ta có: 1 + 1 + a + 1 + 0 + 6 = a + 9
Để số
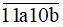chia hết cho 9 thì a + 9 chia hết cho 9 mà a là chữ số nên a = 0 hoặc a = 9.Suy ra 110 106 và 119 106 thỏa mãn chia cho 5 dư 1 và chia hết cho 9.
Vậy có ba số chia hết cho 9, chia 5 dư 1.
Bài 80 trang 27 sách bài tập Toán lớp 6 Tập 1: Không tính giá trị biểu thức, hãy giải thích tại sao mỗi biểu thức sau chia hết cho 3:
a) A = 1 233 + 42 312 + 72 036;
b) B = 111 + 222 + 333 + … + 999.
Lời giải:
a) Ta có: 1 + 2 + 3 + 3 = 9 chia hết cho 3 nên 1 223 chia hết cho 3;
Ta có: 4 + 2 + 3 + 1 + 2 = 12 chia hết cho 3 nên 42 312 chia hết cho 3;
Ta có: 7 + 2 + 0 + 3 + 6 = 18 chia hết cho 3 nên 72 036 chia hết cho 3;
Do đó: 1 233 + 42 312 + 72 036 chia hết cho 3.
Vậy A = 1 233 + 42 312 + 72 036 chia hết cho 3.
b) B = 111 + 222 + 333 + … + 999
= 111 + 2.111 + 3.111 + … + 9.111
= 111.(1 + 2 + 3 + … + 9)
Ta có: 1 + 1 + 1 = 3 chia hết cho 3 nên 111 chia hết cho 3.
Do đó 111.(1 + 2 + 3 + … + 9) chia hết cho 3.
Vậy B = 111 + 222 + 333 + … + 999 chia hết cho 3.
Bài 81 trang 27 sách bài tập Toán lớp 6 Tập 1: Không tính giá trị biểu thức, hãy giải thích tại sao mỗi biểu thức sau chia hết cho 9:
a) P = 81 + 108 + 918;
b) M = 12.585 + 13.63 333 + 14. 378 225 + 18.5 142 312;
c) N = 11 + 22 + 33 + … + 99 + 2 021.60 021.
Lời giải:
a) Ta có: 8 + 1 = 9 chia hết cho 9 nên 81 chia hết cho 9;
Ta có: 1 + 0 + 8 = 9 chia hết cho 9 nên 108 chia hết cho 9;
Ta có: 9 + 1 + 8 = 18 chia hết cho 9 nên 918 chia hết cho 9;
Do đó: 81 + 108 + 918 chia hết cho 9.
Vậy P = 81 + 108 + 918 chia hết cho 9.
b) Ta có: 5 + 8 + 5 =18 chia hết cho 9 nên 585 chia hết cho 9. Do đó 12.585 chia hết cho 9.
Ta có: 6 + 3 + 3 + 3 + 3 = 18 chia hết cho 9 nên 63 333 chia hết cho 9. Do đó 13.63 333 chia hết cho 9.
Ta có: 3 + 7 + 8 + 2 + 2 + 5 = 27 chia hết cho 9 nên 378 225 chia hết cho 9. Do đó 14. 378 225 chia hết cho 9
Ta có: 5 + 1 + 4 + 2 + 3 + 1 + 2 = 18 chia hết cho 9 nên 5 142 312 chia hết cho 9. Do đó 18.5 142 312 chia hết cho 9.
Vậy M = 12.585 + 13.63 333 + 14. 378 225 + 18.5 142 312 chia hết cho 9.
c) N = 11 + 22 + 33 + … + 99 + 2 021.60 021
= (11 + 88) + (22 + 77) + (33 + 66) + (44 + 55) + 99 + 2 021.60 021
= 99 + 99 + 99 + 99 + 99 + 2 021.60 021.
Ta có: 9 + 9 = 18 chia hết cho 9 nên 99 chia hết cho 9;
6 + 0 + 0 + 2 + 1 = 9 chia hết cho 9 nên 60 021 chia hết cho 9. Do đó 2 021.60 021 chia hết cho 9.
Suy ra 99 + 99 + 99 + 99 + 99 + 2 021.60 021 chia hết cho 9.
Vậy N = 11 + 22 + 33 + … + 99 + 2 021.60 021 chia hết cho 9.
Bài 82 trang 27 sách bài tập Toán lớp 6 Tập 1: Tìm các số tự nhiên a, b sao cho:
a)
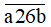chia hết cho cả 2, 3, 5 và 9;b) 123.a + 9 873.b = 2 227 691.
Lời giải:
a) Để số chia hết cho 2, 5 thì b = 0;
Khi đó số cần tìm là:
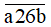
Ta có: a + 2 + 6 + 0 = a + 8;
Để số
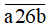chia hết cho 3 và 9 thì a + 8 chia hết cho 3 và 9.Mà a là chữ số và a khác 0 nên a = 1.
Vậy a = 1, b = 0 thì số
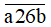chia hết cho cả 2, 3, 5 và 9.b) Ta có 1 + 2 + 3 = 6 chia hết cho 3 nên 123 chia hết cho 3. Do đó 123.a chia hết cho 3.
Ta có: 9 + 8 + 7 + 3 = 27 chia hết cho 3 nên 9 873 chia hết cho 3. Do đó 9 873.b chia hết cho 3.
Vì vậy 123.a + 9 873.b chia hết cho 3.
Ta lại có: 2 + 2 + 2 + 7 + 6 + 9 + 1 = 29 không chia hết cho 3.
Do đó không tồn tại a và b thỏa mãn yêu cầu bài toán.
Bài 83 trang 27 sách bài tập Toán lớp 6 Tập 1:
a) Có bao nhiêu số tự nhiên có hai chữ số chia cho 3 dư 1?
b) Có bao nhiêu số tự nhiên có ba chữ số chia cho 9 dư 2?
c) Có bao nhiêu số tự nhiên có hai chữ số
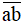sao cho 
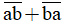chia hết cho 9?Lời giải:
a) Các số tự nhiên có hai chữ số chia cho 3 dư 1 là: 10; 13; …; 97.
Số các số tự nhiên có hai chữ số chia cho 3 dư 1 là: (97 – 10):3 + 1 = 30 số.
Vậy có 30 số tự nhiên có hai chữ số chia cho 3 dư 1.
b) Các số tự nhiên có ba chữ số chia cho 9 dư 2 là: 101; 110; 119; 128; 237; …; 992.
Số các số tự nhiên có ba chữ số chia cho 9 dư 2 là: (992 – 101): 9 + 1 = 100.
Vậy có 100 số tự nhiên có ba chữ số chia cho 9 dư 2.
c) Ta có:
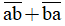= 10a + b + 10b + a = 11a + 11b = 11.(a + b)Vì 11 không chia hết cho 9 nên a + b chia hết cho 9.
Mà a, b là các chữ số nên a, b ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}
Các cặp số (a; b) là: (1; 8), (8; 1), (7; 2), (2; 7), (6; 3) (3; 6), (4; 5), (5; 4), (9; 9), (9; 0) thỏa mãn tổng chia hết cho 9.
Do đó
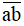∈ {18;81,72;27;63;36;45;54;99;90}.Vậy có tất cả 10 số tự nhiên
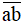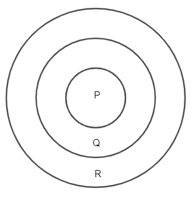
thỏa mãn bài toán.Bài 84 trang 28 sách bài tập Toán lớp 6 Tập 1: Bạn Minh có chơi trò phi tiêu với ba cái tiêu. Lần thứ nhất, bạn Minh phi 2 tiêu vào vùng Q và 1 tiêu vào vùng R thì được 12 điểm. Lần thứ hai, bạn Minh phi 2 tiêu vào vùng P và 1 tiêu vào cùng R thì được 18 điểm. Lần thứ ba, bạn Minh phi trúng mỗi vùng một tiêu. Hỏi số điểm lần thứ ba của bạn Minh có chia hết cho cả 3 và 5 không? Tại sao?
Lời giải:
Tổng số điểm của bạn Minh ở hai lần đầu là: 12 + 18 (điểm).
Vì bạn Minh đã phi 2 tiêu vào vùng Q và 1 tiêu vào vùng R và phi 2 tiêu vào vùng P và 1 tiêu vào cùng R.
Như vậy sau lần thứ nhất và lần thứ hai bạn Minh phi được 2 tiêu vào vùng Q, 2 tiêu R và 2 tiêu vào vùng P.
Suy ra tổng số điểm ba vùng là: 30:2 = 15 (điểm).
Do lần thứ ba, bạn Minh phi trúng mỗi vùng một tiêu nên số điểm lần thứ ba là 15 điểm.
Ta thấy 15 có chữ số tận cùng là 5 nên chia hết cho 5, 1 + 5 = 6 chia hết cho 3 nên 15 chia hết cho 3.
Vậy số điểm lần thứ ba của bạn Minh chia hết cho cả 3 và 5.
Bài 85 trang 28 sách bài tập Toán lớp 6 Tập 1: Cho a là số tự nhiên có 2 004 chữ số và chia hết cho 9. Gọi b là tổng các chữ số của a; c là tổng các chữ số của b và d là tổng các chữ số của c. Tính d.
Lời giải:
Do a chia hết cho 9 nên tổng các chữ số của a chia hết cho 9. Mặt khác b là tổng các chữ số của a nên b chia hết cho 9.
Do b chia hết cho 9 nên tổng các chữ số của b chia hết cho 9. Mặt khác c là tổng các chữ số của b nên c chia hết cho 9.
Do c chia hết cho 9 nên tổng các chữ số của c chia hết cho 9. Mặt khác d là tổng các chữ số của c nên d chia hết cho 9.
Vì a là số tự nhiên có 2 004 chữ số, mỗi chữ số của a đều không vượt quá 9 nên b ≤ 2 004.9 = 18 036. Nghĩa là b có 5 chữ số.
Suy ra c < 9 + 9 + 9 + 9 = 9.5 = 45. Mặt khác c ≠ 0 và c chia hết cho 9 nên suy ra c ∈ {9; 18; 27; 36}.
Ta có d là tổng các chữ số của c nên d = 9 = 1 + 8 = 2 + 7 = 3 + 6.
Vậy d = 9.
Bài 86 trang 28 sách bài tập Toán lớp 6 Tập 1: Viết liên tiếp các số tự nhiên từ 10 đến 99 liền nhau ta được một số tự nhiên. Hỏi số đó chia hết cho 9 hay không? Vì sao?
Lời giải:
Gọi A là số được viết bởi 90 số từ 10 đến 99.
Tổng các chữ số hàng đơn vị của số này là: (0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9). 9 = 405.
Tổng các chữ số hàng chục của số này là: (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9).10 = 450.
Vậy tổng các chữ số của số A là: 405 + 450 = 855.
Vì 8 + 5 + 5 =18 chia hết cho 9 nên 855 chia hết cho 9.
Vậy số A chia hết cho 9.
Bài 87 trang 28 sách bài tập Toán lớp 6 Tập 1: Không thực hiện phép tính, hãy giải thích tại sao phép nhân là sai: 7 654.658 = 5 136 332.
Lời giải:
Ta có: 7 + 6 + 5 + 4 = 22 chia cho 9 dư 4 nên 7 654 chia cho 9 dư 4.
Ta lại có: 6 + 5 + 8 = 19 chia cho 9 dư 1 nên 658 chia cho 9 dư 1.
Do đó 7 654.658 chia 9 dư 4.
Ta có: 5 + 1 + 3 + 6 + 3 + 3 + 2 = 23 chia cho 9 dư 3 nên 5 136 332 chia cho 9 dư 3.
Vậy phép tính 7 654.658 = 5 136 332 là sai.
Bài 88 trang 28 sách bài tập Toán lớp 6 Tập 1: Một công ty có 9 contenơ hàng với khối lượng hàng mỗi contenơ là: 193 tạ, 239 tạ, 277 tạ, 297 tạ, 316 tạ, 321 tạ, 329 tạ, 346 tạ, 355 tạ. Trong sáu tháng đầu năm công ty đó đã xuất khẩu 8 contenơ hàng, trong đó lượng hàng xuất khẩu của Quý II gấp 8 lần Quý I. Contenơ hàng còn lại có khối lượng bằng bao nhiêu?
Lời giải:
Tổng khối lượng hàng của 9 contenơ hàng là:
193 + 239 + 277 + 297 + 316 + 321 + 329 + 346 + 355 = 2 673 (tạ).
Ta có: 2 + 6 + 7 + 3 = 18 chia hết cho 9 nên 2 673 chia hết cho 9.
Vì lượng hàng xuất khẩu của Quý II gấp 8 lần Quý I nên số lượng hàng trong 6 tháng đầu năm phải chia hết cho 9.
Do đó khối lượng hàng của contenơ còn lại phải chia hết cho 9.
Trong số 9 contenơ trên chỉ có contenơ có khối lượng 297 tạ là thỏa mãn chia hết cho 9.
Vậy contenơ hàng còn lại có khối lượng là 297 tạ.
- Lý thuyết Dấu hiệu chia hết cho 2, cho 5 (Cánh diều 2023) hay, chi tiết | Toán lớp 6
Lý thuyết Toán lớp 6 Bài 8: Dấu hiệu chia hết cho 2, cho 5
Video giải Toán 6 Bài 8: Dấu hiệu chia hết cho 2, cho 5 – Cánh diều
A. Lý thuyết Dấu hiệu chia hết cho 2, cho 5
I. Dấu hiệu chia hết cho 2
Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
Ví dụ:
+ Các số 234, 356,… lần lượt có chữ số tận cùng là 4 và 6 nên chúng chia hết cho 2.
+ Các số 1 230, 2 548,… lần lượt có chữ số tận cùng là 0 và 8 nên chúng chia hết cho 2.
II. Dấu hiệu chia hết cho 5
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Ví dụ:
+ Các số 120, 355,… lần lượt có chữ số tận cùng là 0 và 5 nên chúng chia hết cho 5.
+ Các số 1 120, 5 345,… lần lượt có chữ số tận cùng là 0 và 5 nên chúng chia hết cho 5.
Nhận xét: Từ dấu hiệu chia hết cho 2 và 5 ở trên, ta thấy những số chia hết cho cả 2 và 5 là những số có chữ số tận cùng là 0.
Ví dụ: Các số 100, 1 290, … đều chia hết cho cả 2 và 5 và chúng đều có chữ số tận cùng là 0.
B. Bài tập tự luyện
Bài 1. Cho các số 82, 980, 5 975, 49 173, 756 598. Trong các số đó:
a) Số nào chia hết cho 5, nhưng không chia hết cho 2?
b) Số nào chia hết cho 2, nhưng không chia hết cho 5?
c) Số nào không chia hết cho 2 và không chia hết cho 5?
Lời giải:
a) Số chia hết cho 5 nhưng không chia hết cho 2 có chữ số tận cùng là 5.
Nên trong các số đã cho, số chia hết cho 5 nhưng không chia hết cho 2 là: 5 975.
b) Số chia hết cho 2 nhưng không chia hết cho 5 có chữ số tận cùng là 2; 4; 6; 8.
Nên trong các số đã cho, các số chia hết cho 2 nhưng không chia hết cho 5 là: 82; 756 598.
c) Số không chia hết cho 2 và không chia hết cho 5 thì không có tận cùng là 0; 2; 4; 5; 6; 8, hay nói cách khác là các số có chữ số tận cùng là 1; 3; 7; 9 thì không chia hết cho cả 2 và 5.
Do đó, trong các số đã cho số không chia hết cho 2 và không chia hết cho 5 là: 49 173.
Bài 2. Cho số N =
Có bao nhiêu số N sao cho N là số có 5 chữ số khác nhau và N chia cho 5 dư 1 và N chia hết cho 2.Lời giải:
Điều kiện: a, b ∈ {0; 1; 2; 3; ….; 9}
N =
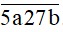chia cho 5 dư 1 nên b ∈ {1; 6}Mà N chia hết cho 2 nên b = 6, ta được số N =
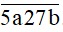
Lại có N là số có 5 chữ số khác nhau nên a ∈ {0; 1; 3; 4; 8; 9}
Vậy có 6 số N thỏa mãn yêu cầu bài là 50 276; 51 276; 53 276; 54 276; 58 276; 59 276.
Xem thêm các bài tóm tắt lý thuyết Toán 6 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 7: Quan hệ chia hết. Tính chất chia hết
Lý thuyết Bài 8: Dấu hiệu chia hết cho 2, cho 5
Lý thuyết Bài 9: Dấu hiệu chia hết cho 3, cho 9
Lý thuyết Bài 10: Số nguyên tố. Hợp số
Lý thuyết Bài 11: Phân tích một số ra thừa số nguyên tố
- Sách bài tập Toán 6 Bài 8 (Cánh diều): Dấu hiệu chia hết cho 2, cho 5
Giải SBT Toán lớp 6 Bài 8: Dấu hiệu chia hết cho 2, cho 5
Bài 66 trang 24 sách bài tập Toán lớp 6 Tập 1: Cho các số 23; 45; 714; 815; 2 300; 2 369; 13 110; 25 555; 4 123 458. Trong các số đó:
a) Số nào chia hết cho 2?
b) Số nào chia hết cho 5?
c) Số nào chia hết cho 2, nhưng không chia hết cho 5?
d) Số nào chia hết cho 5, nhưng không chia hết cho 2?
Lời giải:
a) Các số có tận cùng là các một trong các chữ số: 0; 2; 4; 6; 8 là các số chia hết cho 2.
Trong các số đã cho các số chia hết cho 2 là: 714; 2 300; 13 110; 4 123 458.
b) Các số có chữ số tận cùng là 0 hoặc 5 thì các số đó chia hết cho 5.
Trong các số đã cho các số chia hết cho 5 là: 45; 815; 2 300; 13 110; 25 555.
c) Số chia hết cho 2 nhưng không chia hết cho 5 là: 714; 4 123 458.
d) Số chia hết cho 5 nhưng không chia hết cho 2 là: 45; 815; 25 555.
Bài 67 trang 24 sách bài tập Toán lớp 6 Tập 1: Tìm chữ số x để số
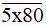thỏa mãn mỗi điều kiện sau:a) Chia hết cho 2;
b) Chia hết cho 5;
c) Chia hết cho cả 2 và 5.
Lời giải:
a) Số
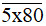có chữ số tận cùng là 0 nên số này luôn chia hết cho 2.Do đó x là chữ số nên có thể nhận tất cả các giá trị {0;1;2;3;4;5;6;7;8;9}.
Vậy x ∈ {0;1;2;3;4;5;6;7;8;9}.
b) Số
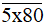có chữ số tận cùng là 0 nên số này luôn chia hết cho 5.Do đó x là chữ số nên có thể nhận tất cả các giá trị {0;1;2;3;4;5;6;7;8;9}.
Vậy x ∈ {0;1;2;3;4;5;6;7;8;9}.
c) Số
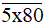có chữ số tận cùng là 0 nên số này luôn chia hết cho 2 và 5.Do đó x là chữ số nên có thể nhận tất cả các giá trị {0;1;2;3;4;5;6;7;8;9}.
Vậy x ∈ {0;1;2;3;4;5;6;7;8;9}.
Bài 68 trang 24 sách bài tập Toán lớp 6 Tập 1: Tìm chữ số x để số
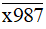thỏa mãn mỗi điều kiện sau:a) Chia hết cho 2;
b) Chia hết cho 5.
Lời giải:
a) Vì
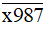có chữ số tận cùng là 7 nên 
không chia hết cho 2.Do đó không tồn tại giá trị nào của chữ số x để số
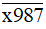chia hết cho 2.Vậy không tồn tại x để
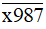chia hết cho 2.b) Vì
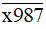có chữ số tận cùng là 7 nên 
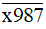không chia hết cho 5.Do đó không tồn tại giá trị nào của chữ số x để số
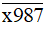chia hết cho 5.Vậy không tồn tại x để
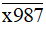chia hết cho 5.Bài 69 trang 24 sách bài tập Toán lớp 6 Tập 1: Tìm chữ số x để số
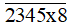thỏa mãn mỗi điều kiện sau:a) Chia hết cho 4;
b) Chia hết cho 8.
Lời giải:
a) Ta có:
= 234508 + 10.x.Vì 234 508 = 4.58 627 nên chia hết cho 4.
Để 234 508 + 10.x chia hết cho 4 thì 10.x phải chia hết cho 4 khi đó x ∈ {0;2;4;6;8}.
Vậy x ∈ {0;2;4;6;8}.
b) Ta có:
= 234508 + 10.x = 234504 + 4 + 10.x.Vì 234 504 = 8.29 313 nên chia hết cho 8.
Để 234 504 + 4 + 10x chia hết cho 8 thì 4 + 10x chia hết cho 8 khi đó x ∈ {2;6}.
Vậy x ∈ {2;6}.
Bài 70 trang 24 sách bài tập Toán lớp 6 Tập 1: Từ các chữ số 0; 5; 7, hãy viết tất cả các số có ba chữ số khác nhau. Sao cho:
a) Các số đó chia hết cho 2;
b) Các số đó chia hết cho 5;
c) Các số đó chia hết cho 5, nhưng không chia hết cho 2;
d) Các số đó chia hết cho cả 2 và 5.
Lời giải:
a) Các số chia hết cho 2 có tận cùng là 0; 2; 4; 6; 8 nên số chia hết cho 2 tạo bởi 3 chữ số 0; 5; 7 là: 570; 750.
b) Các số chia hết cho 5 có tận cùng là 0 hoặc 5 nên số chia hết cho 5 tạo bởi 3 chữ số 0; 5; 7 là: 570; 750; 705.
c) Các số chia hết cho 5 nhưng không chia hết cho 2 là: 705.
d) Các số chia hết cho cả 2 và 5 là: 570; 750.
Bài 71 trang 25 sách bài tập Toán lớp 6 Tập 1: Không tính giá trị biểu thức, hãy giải thích tại sao mỗi biểu thức sau chia hết cho 2:
a) A = 1 234 + 43 312 + 5 436 + 10 988;
b) B = 2 335 + 983 333 + 3 142 311 + 5 437;
c) C = 11 + 22 + 33 + … + 88 + 99 + 2 021;
d) D = 8.51.633.4 445 – 777.888 + 2 020.
Lời giải:
a) Vì 1 234 có chữ số tận cùng là 4 nên chia hết cho 2;
43 312 có chữ số tận cùng là 2 nên chia hết cho 2;
5 436 có chữ số tận cùng là 6 nên chia hết cho 2;
10 988 có chữ số tận cùng là 8 nên chia hết cho 2.
Do đó 1 234 + 43 312 + 5 436 + 10 988 chia hết cho 2.
Vậy A = 1 234 + 43 312 + 5 436 + 10 988 chia hết cho 2.
b) Vì 2 335; 983 333; 3 142 311; 5 437 là các số lẻ nên tổng của 2 335 + 983 333 + 3 142 311 + 5 437 là số chẵn nên chia hết cho 2.
Vậy B = 2 335 + 983 333 + 3 142 311 + 5 437 chia hết cho 2.
c) 11 + 22 + 33 + … + 88 + 99 + 2 021
Vì 11; 33; 55; 77; 99; 2 021 là các số lẻ nên 11 + 33 + 55 + 77 + 99 + 2 021 là một chẵn nên chia hết cho 2.
Mà các số 22; 44; 66; 88 đều là các số chẵn nên chia hết cho 2.
d) Vì 8 chia hết cho 2 nên 8.51.633.4 445 chia hết cho 2; 888 chia hết cho 2 nên 777.888 chia hết cho 2 và 2 020 chia hết cho 2 nên 8.51.633.4 445 – 777.888 + 2 020 chia hết cho 2.
Vậy D = 8.51.633.4 445 – 777.888 + 2 020 chia hết cho 2.
Bài 72 trang 25 sách bài tập Toán lớp 6 Tập 1: Tìm số tự nhiên có ba chữ số giống nhau, biết rằng số đó không chia hết cho 2 nhưng chia hết cho 5.
Lời giải:
Các số chia hết cho 5 có chữ số tận cùng là 0 hoặc 5.
Mà số cần tìm không chia hết cho 2 nên chữ số tận cùng là 5.
Số cần tìm là số có ba chữ số giống nhau nên số đó là: 555.
Vậy số tự nhiên có ba chữ số cần tìm là: 555.
Bài 73 trang 25 sách bài tập Toán lớp 6 Tập 1:
a) Có bao nhiêu số có hai chữ số chia cho 5 dư 4?
b) Có bao nhiêu số có ba chữ số chia cho 2 và cho 5 có cùng số dư?
c) Từ 1 đến 555 có bao nhiêu số chia hết cho 2?
d) Từ 500 đến 1 000 có bao nhiêu số chia hết cho 5?
Lời giải:
a) Các số có hai chữ số chia 5 dư 4 là: 14; 19; 24; 29; 34; 39; 44; …; 94; 99.
Số các số có hai chữ số chia 5 dư 4 là: (99 – 14):5 + 1 = 18.
Vậy có 18 số có hai chữ số chia cho 5 dư 4.
b) Một số chia cho 2 sẽ có số dư là 0; 1.
Một số chia cho 5 sẽ có số dư là: 0; 1; 2; 3; 4.
Do đó, một số chia cho 2 và cho 5 có cùng số dư thì số đó phải chia hết cho cả 2 và 5 hoặc cùng chia cho 2 và cho 5 dư 1.
Trường hợp 1: Các số có ba chữ số cùng chia hết cho 2 và cho 5 là: 100; 110; 120; …; 990.
Số các số có ba chữ số cùng chia hết cho 2 và 5 là: (990 – 100):10 + 1 = 90 số.
Trường hợp 2: Các số có ba chữ số cùng chia cho 2 và cho 5 có số dư là 1 là: 101; 111; 121; …; 991.
Số các số có ba chữ số cùng chia cho 2 và cho 5 dư 1 là: (991 – 101):10 + 1 = 90 số.
Vậy có tất cả 90 + 90 = 180 số có ba chữ số chia cho 2 và cho 5 có cùng số dư.
c) Các số chia hết cho 2 từ 1 đến 555 là: 2; 4; 6; …; 554.
Số các số nằm trong khoảng từ 1 đến 555 chia hết cho 2 là: (554 – 2):2 + 1 = 277 số.
Vậy có 277 số trong các số từ 1 đến 555 chia hết cho 2.
d) Các số từ 500 đến 1 000 chia hết cho 5 là: 500; 505; 510; …; 1000.
Số các số nằm từ 500 đến 1 000 chia hết cho 5 là: (1 000 – 500):5 + 1 = 101 số.
Vậy có tất cả 101 số từ 500 đến 1 000 chia hết cho 5.
Bài 74 trang 25 sách bài tập Toán lớp 6 Tập 1: Một cửa hàng mĩ phẩm miễn thuế ở sân bay có khuyên mãi như sau: Khách cứ mua 10 hộp mĩ phẩm thì được tặng một hộp. Mỗi hộp có giá 53 USD. Công ty A mua 48 hộp mĩ phẩm ở cửa hàng đó. Hỏi số USD công ty phải trả để mua 48 mĩ phẩm trên có chia hết cho 5 không? Vì sao?
Lời giải:
Ta có 48 = 4.10 + 8.
Vì mua 10 hộp được tặng 1 hộp nên trong 40 hộp công ty A mua sẽ được tặng 4 hộp mĩ phẩm nữa nên công ty phải trả tiền cho 44 hộp mĩ phẩm.
Công ty phải trả số tiền để mua 48 hộp mĩ phẩm trên là: 44.53 = 2 332 (USD).
Mà 2 332 có chữ số tận cùng là 2 nên không chia hết cho 5.
Bài 75 trang 25 sách bài tập Toán lớp 6 Tập 1: Chứng tỏ rằng:
a) Tổng của 2 020 số lẻ bất kì luôn chia hết cho 2;
b) 1111 + 2222 + 3333 + 4444 + 5555 không chia hết cho 2;
c) 2 + 22 + 23 + … + 259 + 260 + 561 chia hết cho 5.
Lời giải:
a) Tổng của hai số lẻ bất kì là một số chẵn nên tổng của 2020 số lẻ bất kì là một số chẵn nên chia hết cho 2.
b) Ta có 11 là số lẻ nên 1111 là số lẻ;
33 là số lẻ nên 3333 là số lẻ;
55 là số lẻ nên 5555 là số lẻ;
Khi đó: 1111 + 3333 + 5555 là số lẻ.
Mặt khác 2222; 4444 là các số chẵn nên 2222 + 4444 là số chẵn.
Vậy 1111 + 2222 + 3333 + 4444 + 5555 là số lẻ nên không chia hết cho 2.
c) Xét 2 + 22 + 23 + … + 259 + 260
= (2 + 22 + 23 + 24) + (25 + 26 + 27 + 28) + … + (257 + 258 + 259 + 260)
= 2(1 + 2 + 22 + 23) + 25.(1 + 2 + 22 + 23) + … + 257.(1 + 2 + 22 + 23)
= 2.15 + 25.15 + … + 257.15
= 15.(2 + 25 + … + 257)
Vì 155 nên 15.(2 + 25 + … + 257)5 mà 561 cũng chia hết cho 5.
Nên 2 + 22 + 23 + … + 259 + 260 + 561 chia hết cho 5.
Vậy 2 + 22 + 23 + … + 259 + 260 + 561 chia hết cho 5.
Bài 76 trang 25 sách bài tập Toán lớp 6 Tập 1:
Bạn Duyên sử dụng các khối lập phương để xếp hình. Các hình bạn Duyên xếp được qua các lần được biểu diễn như dưới đây:
Hỏi số khối lập phương bạn Duyên dùng cho lần xếp hình thứ 100 có chia hết cho cả 2 và 5 hay không?
Lời giải:
Qua các lần xếp hình ta thấy số khối lập phương được xếp ở hàng 1 bằng đúng lần đó và các hàng trên giảm dần về 1.
Do đó hàng 1 của lần xếp hình thứ 100 là 100 khối lập phương, hàng tiếp theo là 99 khối, hàng tiếp theo là 98, … đến hàng cuối cùng sẽ có 1 khối lập phương.
Số khối lập phương bạn Duyên dùng cho lần xếp hình thứ 100 là:
100 + 99 + 98 + … + 2 + 1
= (100 + 1) + (99 + 2) + (98 + 3) + … + (50 + 51)
= 101 + 101 + 101 + … + 101
= 101.60
= 5 050.
Ta thấy 5 050 có tận cùng là chữ số 0 nên 5 050 chia hết cho 2 và 5.
Vậy có 5 050 khối lập phương được dùng cho lần xếp hình thứ 100 của bạn Duyên va chia hết cho 2 và 5.
- Lý thuyết Dấu hiệu chia hết cho 3, cho 9 (Chân trời sáng tạo 2023) hay, chi tiết | Toán lớp 6
Lý thuyết Toán lớp 6 Bài 8: Dấu hiệu chia hết cho 3, cho 9
Video giải Toán 6 Bài 8: Dấu hiệu chia hết cho 3, cho 9 – Chân trời sáng tạo
A. Lý thuyết Dấu hiệu chia hết cho 3, cho 9
1. Dấu hiệu chia hết cho 9
Các số có tổng các chữ số chia hết cho 9 thì số đó chia hết cho 9 và chỉ những số đó chia hết cho 9.
Ví dụ:
a) Số 1 944 chia hết cho 9 vì có tổng các chữ số là 1 + 9 + 4 + 4 = 18 chia hết cho 9.
b) Số 7 325 không chia hết cho 9 vì có tổng các chữ số là 7 + 3 + 2 + 5 = 17 không chia hết cho 9.
2. Dấu hiệu chia hết cho 3
Các số có tổng các chữ số chia hết cho 3 thì số đó chia hết cho 3 và chỉ những số đó chia hết cho 3.
Ví dụ:
a) Số 90 156 chia hết cho 3 vì có tổng các chữ số là 9 + 0 + 1 + 5 + 6 = 21 chia hết cho 3.
b) Số 6 116 không chia hết cho 3 vì có tổng các chữ số là 6 + 1 + 1 + 6 = 14 không chia hết cho 3.
B. Bài tập tự luyện
Bài 1. Cho
chia hết cho 9. Tìm số thay thế cho a.Hướng dẫn giải
Tổng các chữ số của
là 1 + a + 3 + 2 = a + 6 = a + 6.Nên để
chia hết cho 9 thì a + 6 phải chia hết cho 9.Do a là các số tự nhiên từ 0 đến 9 nên:
0 + 6 ≤ a + 6 ≤ 9 + 6.
Hay 6 ≤ a + 6 ≤ 15.
Số chia hết cho 9 từ 6 đến 15 chỉ có đúng một số là 9 nên a + 6 = 9
Do đó a = 3.
Vậy số thay thế cho a chỉ có thể là 3.
Bài 2: Cho
chia hết cho 3 và chia hết cho 9. Hãy tìm chữ số z.Hướng dẫn giải
Vì một số bất kỳ nếu chia hết cho 9 thì cũng chia hết cho 3 nên ta chỉ xét
chia hết cho 9.Để
⋮ 9 thì (5 + z + 8 + 9) ⋮ 9Hay (22 + z) ⋮ 9 nên z = 5.
Vậy với z = 5 thì
chia hết cho 3 và chia hết cho 9.Bài 3. Tổng (hiệu) sau chia hết cho 3 hay 9?
a) 1251 + 5316;
b) 5436 – 1324;
c) 1 . 2 . 3 . 4 . 5 . 6 + 27.
Hướng dẫn giải
a) Tổng các chữ số của 1251 là 1 + 2 + 5 + 1 = 9 chia hết cho 3 và 9.
Tổng các chữ số của 5 316 là 5 + 3 + 1 + 6 = 15 chia hết cho 3 nhưng không chia hết cho 9.
Vậy 1251 + 5316 chia hết cho 3 nhưng không chia hết cho 9.
b) Tổng các chữ số của 5436 có 5 + 4 + 3 + 6 = 18 chia hết cho 3 và 9.
Tổng các chữ số của 1324 có 1 + 3 + 2 + 4 = 10 không chia hết cho 3 và 9.
Vậy 5436 – 1324 không chia hết cho 3 và 9.
c) Tích 1 . 2 . 3 . 4 . 5 . 6 chia hết cho 3 (vì tích này có thừa số là 3).
Ta có: 1 . 2 . 3 . 4 . 5 . 6
= 1 . 2 . 3 . 4 . 5 . (3 . 2)
= 1 . 2 . 4 . 5 . (3 . 3) . 2
= 1 . 2 . 4 . 5 . 9 . 2 chia hết cho 9 (vì nó có thừa số là 9).
Do đó 1 . 2 . 3 . 4 . 5 . 6 chia hết cho 3 và 9.
Tổng các chữ số của 27 là 2 + 7 = 9 chia hết cho 3 và 9.
Vậy 1 . 2 . 3 . 4 . 5 . 6 + 27 chia hết cho 3 và 9.
Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 7: Dấu hiệu chia hết cho 2, cho 5
Lý thuyết Bài 8: Dấu hiệu chia hết cho 3, cho 9
Lý thuyết Bài 9: Ước và bội
Lý thuyết Bài 10: Số nguyên tố, Hợp số, Phân tích một số ra thừa số nguyên tố
Lý thuyết Bài 11: Ước chung, Ước chung lớn nhất