Câu hỏi:
Hãy đếm xem trong hình bên có bao nhiêu hình vuông, bao nhiêu hình chữ nhật.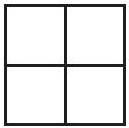
Trả lời:
Đặt tên các điểm như hình vẽ dưới: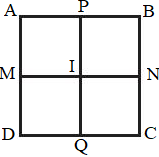
+) Số hình vuông có trong hình bên là 5 hình gồm: hình vuông ABCD, APIM, PBNI, INCQ, MIQD. +) Số hình chữ nhật có trong hình bên là 4 hình gồm hình chữ nhật ABNM, MNCD, APQD, PBCQ.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Lý thuyết Toán lớp 6 Chương 4 (Chân trời sáng tạo 2023): Một số yếu tố thống kê hay, chi tiết
Lý thuyết Toán lớp 6 Chương 4: Một số yếu tố thống kê
Video giải Toán 6 Chương 4: Một số yếu tố thống kê – Chân trời sáng tạo
A. Lý thuyết Toán lớp 6 Chương 4: Một số yếu tố thống kê
1. Dữ liệu
a) Thu thập dữ liệu
• Những thông tin thu thập được như: số, chữ, hình ảnh,… được gọi là dữ liệu. Dữ liệu dưới dạng số được gọi là số liệu.
• Số liệu là một loại dữ liệu nhưng dữ liệu chưa chắc là số liệu.
• Các cách thu thập dữ liệu: Quan sát, lập phiếu điều tra (phiếu hỏi), thu thập từ nguồn có sẵn (sách, báo, trang web…).
b) Phân loại dữ liệu
• Phân loại dữ liệu là ta đi sắp xếp các thông tin theo những tiêu chí nhất định.
c) Tính hợp lí của dữ liệu
• Để đánh giá tính hợp lí của dữ liệu, ta cần đưa ra các tiêu chí đánh giá, chẳng hạn như dữ liệu phải:
– Đúng định dạng: Họ tên phải là chữ, số tuổi phải là số, email thì phải có kí hiệu @…
– Nằm trong phạm vi dự kiến: Số người thì phải là số tự nhiên, cân nặng của người Việt Nam thường dưới 200kg, số tuổi là số nguyên dương,..
2. Bảng thống kê (bảng dữ liệu)
a) Bảng dữ liệu ban đầu
• Bảng dữ liệu ban đầu là bảng mà ta tạo ra để ghi lại các thông tin đã thu thập được khi điều tra một vấn đề nào đó.
Chú ý: Để thu thập các dữ liệu được nhanh chóng, trong bảng dữ liệu ban đầu ta thường viết tắt các giá trị, nhưng để tránh sai sót, các giá trị khác nhau phải viết tắt khác nhau.
b) Bảng thống kê (bảng dữ liệu)
• Bảng thống kê là một cách trình bày dữ liệu chi tiết hơn bảng dữ liệu ban đầu.
• Trong bảng thông kê có:
– Đối tượng thống kê: ta cần tìm số liệu của đối tượng nào thì đó là đối tượng thống kê. Các đối tượng này được biểu diễn ở dòng đầu tiên của bảng.
– Tiêu chí thống kê: Thông tin, đặc điểm của mỗi đối tượng.
– Ứng với mỗi đối tượng thống kê có một số liệu thống kê theo tiêu chí, lần lượt được biểu diễn ở dòng thứ hai.
3. Biểu đồ tranh
a) Khái niệm
• Biểu đồ tranh sử dụng biểu tượng hoặc hình ảnh để biểu diễn dữ liệu.
Một biểu tượng (một hình ảnh) có thể thay thế cho một số các đối tượng.
b) Cách đọc biểu đồ tranh
• Bước 1: Xác định biểu tượng (hình ảnh) có thể thay thế cho bao nhiêu đối tượng.
• Bước 2: Lấy số lượng nhân với số thay thế vừa xác định để tìm số liệu cho đối tượng tương ứng.
c) Cách bước vẽ biểu đồ tranh
• Bước 1: Chuẩn bị
– Chọn biểu tượng (hình ảnh) đại diện cho dữ liệu cần biểu diễn.
– Xác định mỗi biểu tượng (hình ảnh) thay thế cho bao nhiêu đối tượng.
• Bước 2: Vẽ biểu đồ tranh
– Biểu đồ tranh thường gồm 2 cột:
– Cột 1: Danh sách phân loại đối tượng thống kê.
+ Cột 2: Vẽ các biểu tượng thay thế đủ số lượng các sối tượng.
• Bước 3: Ghi tên biểu đồ và các chú thích số lượng tương ứng với mỗi biểu tượng của biểu đồ tranh.
4. Biểu đồ cột
a) Khái niệm
• Việc thể hiện dữ liệu bằng biểu đồ tranh trong một số trường hợp sẽ tốn nhiều thời gian và khó thực hiện. Ta có các khác để biểu thị dữ liệu. Đó là vẽ các cột có chiều rộng không đổi, cách đều nhau và có chiều cao đại diện cho số liệu đã cho. Biểu đồ biểu diễn dữ liệu như vậy được gọi là biểu đồ cột.
b) Đọc biểu đồ cột
• Khi đọc biểu đồ cột, ta nhìn theo một trục để đọc danh sách các đối tượng thống kê và nhìn theo trục còn lại để đọc số liệu thống kê tương ứng với các đối tượng đó (lưu ý thang đo trục số liệu khi đọc số liệu).
c) Vẽ biểu đồ cột
• Bước 1: Vẽ hai trục ngang và dọc vuông góc với nhau
– Trục ngang ghi danh sách đối tượng.
– Trục dọc chọn khoảng chia thích hợp với dữ liệu và ghi ở các vạch chia.
• Bước 2: Tại vị trí các đối tượng trên trục ngang, vẽ các cột hình chữ nhật.
– Cách đều nhau
– Có cùng chiều rộng
– Có chiều cao thể hiện số liệu của các đối tượng tương ứng với khoảng chia trên trục dọc.
• Bước 3: Hoàn thiện biểu đồ
– Ghi tên biểu đồ
– Ghi tên các trục và số liệu tương ứng trên mỗi cột (nếu cần).
5. Biểu đồ cột kép
a) Khái niệm
• Để so sánh một cách trực quan từng cặp số liệu của hai bộ dữ liệu cùng loại, người ta ghép 2 biểu đồ cột thành một biểu đồ cột kép.
b) Đọc biểu đồ cột kép
• Khi đọc biểu đồ cột kép, ta nhìn theo một trục để đọc danh sách các đối tượng thống kê và nhìn theo trục còn lại để đọc số liệu thống kê tương ứng với các đối tượng đó (lưu ý thang đo của trục số liệu khi đọc số liệu).
• Dựa vào biểu đồ ta có thể so sánh một các trực quan từng cặp số liệu cả hai bộ giữ liệu cùng loại.
c) Vẽ biểu đồ cột kép
• Bước 1: Vẽ 2 trục ngang và dọc vuông góc với nhau
– Trục ngang ghi danh sách đối tượng.
– Trục dọc chọn khoản chia thích hợp với dữ liệu và ghi ở các vạch chia.
• Bước 2: Tại vị trí từng đối tượng trên trục ngang, vẽ 2 cột hình chữ nhật
– Cách đều nhau.
– Có cùng chiều rộng.
– Có chiều cao thể hiện số liệu của các đối tượng, tương ứng với khoảng chia trên trục dọc.
• Bước 3: Hoàn thiện biểu đồ
– Tô màu hoặc ghi gạch chéo để phân biệt hai cột trong cột kép.
– Ghi tên biểu đồ.
– Ghi tên các trục và số liệu tương ứng trên mỗi cột (nếu cần).
B. Bài tập vận dụng
Bài 1. Thân nhiệt của bệnh nhân A trong 10 tiếng được theo dõi và ghi lại trong bảng như sau (đơn vị là oC):
38
38,5
39
40
40,5
88
38
39
39,5
38
Tìm điểm không hợp lí trong bảng dữ liệu trên.
Hướng dẫn giải:
Điểm không hợp lí ở đây là 88oC vì con người chúng ta nhiệt độ cơ thể không thể lên tới 88oC.
Bài 2. Bảng sau cho biết số anh chị em ruột trong gia đình của 30 học sinh lớp 6A
Số anh chị em ruột 0 1 2 3 Số học sinh 9 6 7 8 a) Đối tượng thông kê và tiêu chí thống kê của bảng trên là gì?
b) Có bao nhiêu bạn học sinh không có anh chị em ruột.
Hướng dẫn giải:
a) Ta cần tìm thông tin số anh chị em ruột nên đối tượng thống kê là 0; 1; 2; 3.
Tiêu chí thống kê là số học sinh ứng với số anh chị em ruột.
b) Với đối tượng là “Số anh chị em ruột bằng 0” thì có 9 học sinh.
Bài 3. Biểu đồ tranh thể hiện số ti vi (TV) bán được qua các năm của 1 siêu thị điện máy.
a) Năm nào có số lượng ti vi bán được nhiều nhất? Số ti vi bán được là bao nhiêu?
b) Năm nào số lượng ti vi bán được ít nhất? Số lượng ti vi bán được là bao nhiêu?
Hướng dẫn giải:
a) Năm bán được nhiều ti vi nhất là năm 2020 (6 biểu tượng).
Số ti vi bán được năm 2020 là:
6.500 = 3000 (ti vi)
b) Năm bán được ít ti vi nhất là năm 2018 (1,5 biểu tượng)
Số ti vi bán được năm 2018 là:
1.500 + 250.1 = 750 (ti vi).
Bài 4. Sản lượng khai thác và nuôi trồng của nước ta các năm từ năm 2000 đến năm 2015 được thể hiện trong bảng (đơn vị nghìn tấn) sau:
2000
2005
2010
2015
Khái thác
1660,9
1987,9
2414,4
3226,1
Nuôi trồng
589,6
1478
2728,3
3644,6
Vẽ biểu đồ cột kép thể hiện sản lượng khai thác và nuôi trồng của nước ta từ năm 2000 đến năm 2015.
Hướng dẫn giải:
• Bước 1: Vẽ 2 trục ngang và dọc vuông góc với nhau
– Trục ngang ghi các năm 2000; 2005; 2010; 2015..
– Trục dọc chọn khoản chia thích hợp với dữ liệu và ghi ở các vạch chia (đơn vị nghìn tấn).
• Bước 2: Tại vị trí từng đối tượng trên trục ngang, vẽ 2 cột hình chữ nhật
– Cách đều nhau.
– Có cùng chiều rộng.
– Có chiều cao thể hiện số liệu của các đối tượng, tương ứng với khoảng chia trên trục dọc.
• Bước 3: Hoàn thiện biểu đồ
– Tô màu xanh cho cột thể hiện khai thác và màu đỏ cho cột thể hiện nuôi trồng. – Ghi tên
– Ghi tên biểu đồ.
Biểu đồ sản lượng khai thác và nuôi trồng hải sản của nước taTừ năm 2000 đến năm 2015
Bài 5. Dân số Hoa Kỳ từ năm 1800 đến 2005 đực thể hiện trong bảng thống kê sau:
Năm
1800
1820
1840
1860
1880
1900
1920
1940
1960
1980
2005
Dân số
(triệu người)
5
10
17
31
50
76
105
132
179
227
296,5
a) Vẽ biểu đồ cột thể hiện dân số của Hoa Kỳ từ năm 1800 đến năm 2005.
b) Em có nhận xét gì về dân số Hoa Kỳ từ năm 1800 đến năm 2005.
c) Em hãy so sánh dân số Hoa Kỳ năm 1960 và năm 1860.
Hướng dẫn giải:
a)
• Bước 1: Vẽ hai trục ngang và dọc vuông góc với nhau
– Trục ngang ghi các năm.
– Trục dọc chọn khoảng chia thích hợp với đơn vị triệu người và ghi ở các vạch chia.
• Bước 2: Tại vị trí các đối tượng trên trục ngang, vẽ các cột hình chữ nhật
– Cách đều nhau.
– Có cùng chiều rộng.
– Có chiều cao thể hiện số liệu của các đối tượng tương ứng với khoảng chia trên trục dọc.
• Bước 3: Hoàn thiện biểu đồ
– Ghi tên biểu đồ: Biểu đồ dân số Hoa Kỳ giai đoạn 1800 – 2005.
– Ghi tên các trục và số liệu tương ứng trên mỗi cột (nếu cần).
b) Ta nhận thấy dân số Hoa Kỳ từ năm 1800 đến năm 2005 tăng nhanh và không có dấu hiệu giảm suốt.
c) Năm 1960 dân số Hoa Kỳ là 179 triệu người; năm 1860 dân số Hoa Kỳ là 32 triệu người. Ta có thể thấy dân số Hoa Kỳ năm 1960 lớn hơn nhiều lần dân số Hoa Kỳ năm 1860.
Bài 6. Hưởng ứng Tết trồng cây, trường THCS Thiệu Hợp đã phát động phong trào trồng cây ở khối lớp 8 và khối lớp 9. Số cây mỗi khối trồng được được thể hiện trong biểu đồ sau:
a) Em hãy cho biết hai khối lớp 8 và lớp 9 của trường THCS Thiệu Hợp đã trồng được tất cả bao nhiêu cây?
b) Nếu cứ hai học sinh trồng được 1 cây thì khối lớp 9 của trường THCS Thiệu Hợp có bao nhiêu học sinh?
Hướng dẫn giải:
a) Số cây khối 8 trồng được là:
3.20 + 1.10 = 70 (cây)
Số cây khối 9 trồng được là:
4.20 = 80 (cây)
Khối lớp 8 và khối lớp 9 trường THCS Thiệu Hợp trồng được số cây là:
70 + 80 = 150 (cây)
b) Nếu cứ hai học sinh trồng được 1 cây thì số học sinh khối 9 của trường THCS Thiệu Hợp là:
80.2 = 160 (học sinh)
Vậy hai khối lớp 8 và lớp 9 trồng được 150 cây và khối lớp 9 có 160 học sinh.
Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Chương 3: Hình học trực quan và hình học phẳng trong thực tiễn
Lý thuyết Chương 4: Một số yếu tố thống kê
Lý thuyết Chương 5: Phân số
Lý thuyết Chương 6: Số thập phân
Lý thuyết Chương 7: Hình học trực quan
- Lý thuyết Toán lớp 6 Chương 4: Một số hình phẳng trong thực tiễn (Kết nối tri thức 2023) hay, chi tiết
Lý thuyết Toán lớp 6 Chương 4: Một số hình phẳng trong thực tiễn
Video giải Toán 6 Chương 4: Một số hình phẳng trong thực tiễn – Kết nối tri thức
A. Lý thuyết Toán lớp 6 Chương 4: Một số hình phẳng trong thực tiễn
1. Hình tam giác đều
Trong tam giác đều:
– Ba cạnh bằng nhau.
– Ba góc bằng nhau và bằng 600C.
2. Hình vuông
Trong hình vuông:
– Bốn cạnh bằng nhau.
– Bốn góc bằng nhau và bằng 900.
– Hai đường chéo bằng nhau.
3. Hình lục giác đều
Hình lục giác đều có:
– Sáu cạnh bằng nhau.
– Sáu góc bằng nhau, mỗi góc bằng 1200.
– Ba đường chéo chính bằng nhau.
4. Hình chữ nhật
Trong hình chữ nhật có:
– Bốn góc bằng nhau và bằng 900C.
– Các cặp cạnh đối bằng nhau.
– Hai đường chéo bằng nhau.
5. Hình thoi
Trong hình thoi :
– Bốn cạnh bằng nhau.
– Hai đường chéo vuông góc với nhau.
– Các cặp góc đối bằng nhau.
6. Hình bình hành
Trong hình bình hành:
– Các cặp cạnh đối bằng nhau.
– Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
– Các cặp cạnh đối song song.
– Các cặp góc đối bằng nhau.
7. Hình thang cân
Trong hình thang cân:
– Hai cạnh bên bằng nhau.
– Hai đường chéo bằng nhau.
– Hai cạnh đáy song song với nhau.
– Hai góc kề một đáy bằng nhau.
8. Công thức tính chu vi, diện tích hình vuông, hình chữ nhật và hình thang
Hình vuông cạnh a:
Chu vi: C = 4a.
Diện tích: S = a2.
Hình chữ nhật có chiều dài là a, chiều rộng là b:
Chu vi: C = 2(a + b).
Diện tích: S = a.b.
Hình thang có độ dài hai cạnh đáy là a, b chiều cao h:
Chu vi: C = a + b + c + d.
Diện tích: S = (a + b).h:2.
9. Chu vi, diện tích hình bình hành, hình thoi.
Hình bình hành:
Chu vi: C = 2(a + b).
Diện tích: S = a.h.
Hình thoi:
Chu vi: C = 4.m.
Diện tích: S =
ab .B. Bài tập
Bài 1. Tính diện tích và chu vi các hình được tô màu sau:
Lời giải
a)
Chu vi của hình đã cho là: 8 + 6 + 5 + 7 + (8 + 5) +1 = 40 (cm).
Chia hình ban đầu thành hai hình như hình vẽ. Khi đó ta có:
Diện tích hình chữ nhật to là: 5.7 = 35(cm2)
Diện tích hình chữ nhật nhỏ là: 8.(7 – 6) = 8(cm2)
Diện tích hình ban đầu là: 35 + 8 = 43(cm2)
Vậy diện tích hình được tô màu là 43cm2 và chu vi hình được tô màu là 40 cm.
b)
Chu vi hình được tô màu là: 9 + 4 + 5 + 3 + 5 + 4 + 9 + 17 = 56 (m).
Diện tích hình chữ nhật là: 9.17 = 153 (m2).
Diện tích hình thang cân là: (9 + 3).(9 – 5):2 = 24 (m2).
Diện tích phần được tô màu bằng diện tích hình chữ nhật trừ đi diện tích hình thang cân màu trắng. Khi đó diện tích phần tô màu là: 153 – 24 = 129 (m2).
Vậy chu vi hình được tô màu là 56m, diện tích phần tô màu là 129m2.
Bài 2. Một mảnh vườn có hình dạng như hình vẽ bên. Để tính diện tích mảnh vườn, người ta chia nó thành hình thang cân ABCD và hình bình hành ADEF có kích thước như sau: BC = 30 m; AD = 42 m, BM = 22 m, EN = 28 m. Hãy tính diện tích mảnh vườn này.
Lời giải
Diện tích hình thang cân ABCD là: (30 + 42).22:2 = 792 (m2).
Diện tích hình bình hành ADEF là: 42.28 = 1176 (m2)
Diện tích mảnh vườn là: 792 + 1176 = 1968(m2).
Vậy diện tích mảnh vườn là 1968m2
Bài 3. Một khu vườn hình chữ nhật có chiều dài 25 m, chiều rộng 15 m. Ở giữa khu vườn người ta xây một bồn hoa hình thoi có độ dài hai đường chéo là 5 m và 3 m. Tính diện tích phần còn lại của khu vườn.
Lời giải
Diện tích khu vườn hình chữ nhật là: 25.15 = 375 (m2)
Diện tích bồn hoa hình thoi là: 5.3:2 = 7,5 (m2)
Diện tích phần còn lại của mảnh vườn là: 375 – 7,5 = 367,5 (m2)
Vậy diện tích phần còn lại là 367,5 m2.
Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Chương 3: Số nguyên
Lý thuyết Chương 4: Một số hình phẳng trong thực tiễn
Lý thuyết Chương 5: Tính đối xứng của hình phẳng trong tự nhiên
Lý thuyết Chương 6: Phân số
Lý thuyết Chương 7: Số thập phân
- Sách bài tập Toán 6 (Kết nối tri thức) Ôn tập chương 4 trang 75, 76, 77
Giải SBT Toán lớp 6 Ôn tập chương 4 trang 75, 76, 77
Câu hỏi (Trắc Nghiệm)
Bài 1 trang 75 sách bài tập Toán lớp 6 Tập 1:Trong các hình dưới đây (H.4.21), hình nào là hình thang cân?
(A) Hình (1) (B) Hình (2)
(C) Hình (3) (D) Hình (4)
Lời giải:
Trong các hình trên ta thấy hình (2) là hình thang cân vì có hai đáy song song với nhau và hai cạnh bên bằng nhau.
Đáp án cần chọn là: B
Bài 2 trang 75 sách bài tập Toán lớp 6 Tập 1 Trong các hình dưới đây (H.4.22), hình nào là hình bình hành?
(A) Hình (1) (B) Hình (2)
(C) Hình (3) (D) Hình (4)
Lời giải:
Trong các hình trên ta thấy hình (4) là hình bình hành vì có hai cặp cạnh đối bằng nhau.
Đáp án cần chọn là: D
Bài 3 trang 75 sách bài tập Toán lớp 6 Tập 1: Khẳng định nào sau đây là đúng?
Trong hình chữ nhật:
(A) Bốn góc bằng nhau và bằng 60o;
(B) Hai đường chéo không bằng nhau;
(C) Bốn góc bằng nhau và bằng 90o;
(D) Hai đường chéo song song với nhau.
Lời giải:
Trong hình chữ nhật có bốn góc bằng nhau và bằng 90o
Đáp án cần chọn là: C
Bài 4 trang 75 sách bài tập Toán lớp 6 Tập 1: Khẳng định nào sau đây là đúng?
Trong hình lục giác đều:
(A) Các góc bằng nhau và bằng 90o;
(B) Đường chéo chính bằng đường chéo phụ;
(C) Các góc bằng nhau và bằng 60o;
(D) Các đường chéo chính bằng nhau.
Lời giải:
Trong hình lục giác đều có các đường chéo chính bằng nhau.
Đáp án cần chọn là: D
Bài 5 trang 76 sách bài tập Toán lớp 6 Tập 1: Khẳng định nào sau đây là sai?
(A) Hai đường chéo của hình vuông bằng nhau;
(B) Hai góc kề một đáy của hình thang cân bằng nhau;
(C) Trong hình thoi, các góc đối không bằng nhau;
(D) Trong hình chữ nhật, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Lời giải:
Trong hình thoi, các góc đối bằng nhau nên đáp án C sai.
Đáp án cần chọn là: C
Bài 6 trang 76 sách bài tập Toán lớp 6 Tập 1: Hình vuông có cạnh 10cm thì chu vi của nó là:
(A) 100 cm2 (B) 40 cm;
(D) 40 cm2 (D) 80 cm.
Lời giải:
Chu vi hình vuông cạnh 10cm là:
10. 4 = 40 (cm)
Bài 7 trang 76 sách bài tập Toán lớp 6 Tập 1: Hình chữ nhật có diện tích 800 m2 , độ dài một cạnh là 40m thì chu vi của nó là:
(A) 100 m; (B) 60 m
(C) 120 m (D) 1 600 m.
Lời giải:
Độ dài cạnh còn lại của hình chữ nhật là:
800: 40 = 20 (m)
Chu vi của hình chữ nhật là:
2. (40 + 20) = 120 (m)
Đáp án cần chọn là: C
Bài 8 trang 76 sách bài tập Toán lớp 6 Tập 1: Hình thoi có độ dài hai đường chéo lần lượt là 6cm, 8cm thì diện tích của nó là:
(A) 48 cm2 (B) 14 cm2
(C) 7 cm2 (D) 24 cm2
Lời giải:
Diện tích hình thoi là:
Đáp án cần chọn là: D
Bài 9 trang 76 sách bài tập Toán lớp 6 Tập 1: Hình bình hành có độ dài một cạnh bằng 10 cm và chiều cao tương ứng bằng 5 cm thì diện tích của hình bình hành đó là:
(A) 50 cm; (B) 50 cm2
(C) 25 cm2 (D) 30 cm2
Lời giải:
Diện tích của hình bình hành đó là:
10. 5 = 50 (cm2)
Đáp án cần chọn là: B
Bài 10 trang 76 sách bài tập Toán lớp 6 Tập 1: Hình thang cân có độ dài hai đáy lần lượt là 4cm, 10cm và chiều cao bằng 4cm thì diện tích của hình thang cân đó là:
(A) 14 cm2 (B) 56 cm2
(C) 28 cm2 (D) 160 cm2
Lời giải:
Diện tích hình thang cân là:
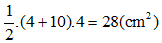
Đáp án cần chọn là: C
Bài tập
Bài 4.29 trang 76 sách bài tập Toán lớp 6 Tập 1: Vẽ hình theo yêu cầu sau:
a) Hình vuông có độ dài cạnh bằng 3, 5cm;
b) Hình chữ nhật có độ dài một cạnh bằng 6cm và diện tích bằng 48 cm2
c) Hình thoi có độ dài cạnh bằng 6cm và một góc bằng 60o.
d) Hình bình hành có độ dài hai cạnh liên tiếp bằng 4cm và 6cm, chiều cao bằng 3cm.
Lời giải:
a) Vẽ hình vuông ABCD có cạnh 3,5 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 3,5 cm.
Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Xác định điểm D trên đường thẳng đó sao cho AD = 3,5 cm.
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Xác định điểm C trên đường thẳng đó sao cho BC = 3,5 cm.
Bước 4. Nối C với D ta được hình vuông ABCD
b) Hình chữ nhật có độ dài một cạnh bằng 6cm và diện tích bằng 48 cm2
Độ dài còn lại của hình chữ nhật là: 48: 6 = 8 (cm)
Vẽ hình chữ nhật ABCD có một cạnh bằng 8 cm, một cạnh bằng 6 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 8 cm.
Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Trên đường thẳng đó lấy điểm D sao cho AD = 6 cm.
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Trên đường thẳng đó lấy điểm C sao cho BC = 6 cm.
Bước 4. Nối D với C ta được hình chữ nhật ABCD.
c) Vẽ hình thoi MNPQ có cạnh MN = 6cm bằng ê ke có góc bằng 60o theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng MN = 6cm
Bước 2: Đặt ê ke có góc 60o trùng với điểm M, kẻ đường thẳng Mx
Bước 3: Trên đường thẳng Mx lấy điểm Q sao cho MQ = 6cm.
Bước 4. Vẽ đường thẳng đi qua Q song song với MN, đường thẳng qua N song song với MQ, hai đường thẳng này cắt nhau tại P. Ta được hình thoi MNPQ.
Xoay hình ta được:
d) Hình bình hành có độ dài hai cạnh liên tiếp bằng 4cm và 6cm, chiều cao bằng 3cm.
Bước 1: Vẽ đoạn thẳng AB = 6cm, đoạn thẳng AH vuông góc với AB có AH = 3cm.
Bước 2: Qua H kẻ đường thẳng Hx song song với AB
Bước 3: Trên tia Hx lấy điểm C sao cho AC = 4cm
Bước 4: Qua B kẻ đường thẳng song song với AC cắt Hx tại D. Ta được hình bình hành ABDC có độ dài như hình vẽ
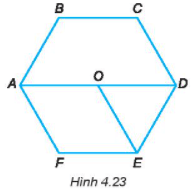
Bài 4.30 trang 77 sách bài tập Toán lớp 6 Tập 1: Quan sát Hình 4.23, kiểm tra và gọi tên hình lục giác đều, hình thoi, hình tam giác đều.
Lời giải:
Sử dụng thước thẳng để đo, ta nhận thấy:
+) AB = BC = CD = DE = EF = FA nên ABCDEF là hình lục giác đều.
+) AO = OE = EF = FA nên AOEF là hình thoi.
+) OD = DE = OE nên tam giác ODE là tam giác đều.
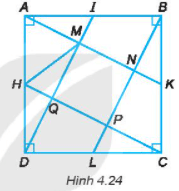
Bài 4.31 trang 77 sách bài tập Toán lớp 6 Tập 1: Quan sát Hình 4.24:
a) Kiểm tra xem tứ giác MNPQ có là hình vuông không?
b) Tứ giác MKCH có là hình thang cân không?
Lời giải:
+) Dùng ê ke kiểm tra ta thấy tứ giác MNPQ có các góc M, góc N, góc P, góc Q đều bằng 90o
+) Dùng thước thẳng đo ta thấy MN = NP = PQ = QM
Do đó tứ giác MNPQ là hình vuông.
+) Vì tứ giác MNPQ là hình vuông nên MN và PQ là hai đường thẳng song song với nhau hay MK và HC là hai đường thẳng song song với nhau.
Mặt khác dùng thước thẳng đo ta thấy MC = HK nghĩa là hai đường chéo bằng nhau.
Do đó tứ giác MKCH là hình thang cân.
Bài 4.32 trang 77 sách bài tập Toán lớp 6 Tập 1: Hãy cắt miếng bìa hình chữ nhật có độ dài hai cạnh là 4cm và 9cm (H.4.25) thành bốn mảnh rồi ghép bốn mảnh này (không chồng lên nhau) để tạo thành một hình vuông.
Lời giải:
Cách 1: Cắt hình chữ nhật thành 4 hình chữ nhật nhỏ theo nét đứt rồi ghép lại thành hình vuông ta được:
Cách 2:
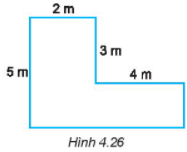
Bài 4.33 trang 77 sách bài tập Toán lớp 6 Tập 1: Một mảnh sân nhà có hình dạng và kích thước như Hình 4.26.
a) Tính diện tích mảnh sân.
b) Nếu lát sân bằng những viên gạch hình vuông có cạnh 50 cm thì cần bao nhiêu viên gạch?
Lời giải:
Ta kẻ thêm như hình vẽ dưới:
a) Cách 1:
Diện tích mảnh sân chính là diện tích hình chữ nhật trừ đi diện tích S của hình chữ nhật có chiều dài 4m, chiều rộng 3m
Chiều dài của hình chữ nhật to là:
2 + 4 = 6 (m)
Diện tích hình chữ nhật to là:
5. 6 = 30 (m2)
Diện tích hình chữ nhật S là:
4. 3 = 12(m2)
Diện tích của mảnh vườn là:
30 – 12 = 18 (m2)
Cách 2:
Ta có thể chia mảnh sân thành hai hình chữ nhật gồm hình 1 và hình 2 như hình vẽ dưới:
Diện tích của hình 1 là:
5. 2 = 10 (m2)
Chiều rộng của hình 2 là:
5 – 3 = 2 (m)
Diện tích của hình 2 là:
4. 2 = 8 (m2)
Diện tích của mảnh vườn là:
10 + 8 = 18 (m2)
b) Đổi 50 cm = 0,5 m
Diện tích một viên gạch lát là:
0,5. 0,5 = 0,25(m2)
Số viên gạch dùng để lát sân là:
18: 0,25 = 72 (viên)
Vậy diện tích mảnh sân là 18 m2 và cần dùng 72 viên gạch để lát sân.
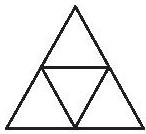
- Hãy đếm số hình tam giác đều, số hình thang cân và số hình thoi trong hình vẽ bên
Câu hỏi:
Hãy đếm số hình tam giác đều, số hình thang cân và số hình thoi trong hình vẽ bên
Trả lời:
Đặt tên như hình vẽ dưới đây:
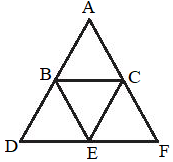Trong hình vẽ trên có:+) Số hình tam giác đều là 5 hình gồm: tam giác đều ABC, BCE, BED, CEF, ADF.+) Số hình thang cân là 3 hình gồm: BCFD, ACED, ABEF.+) Số hình thoi là 3 hình gồm: ABEC, BCFE, BCED.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Vẽ hình theo các yêu cầu sau:a) Hình tam giác đều có cạnh bằng 5 cm.b) Hình vuông có cạnh bằng 6 cm.c) Hình chữ nhật có chiều dài 4 cm, chiều rộng 3 cm.
Câu hỏi:
Vẽ hình theo các yêu cầu sau:a) Hình tam giác đều có cạnh bằng 5 cm.b) Hình vuông có cạnh bằng 6 cm.c) Hình chữ nhật có chiều dài 4 cm, chiều rộng 3 cm.
Trả lời:
a) Vẽ tam giác đều ABC cạnh 5cm theo hướng dẫn sau:Bước 1. Vẽ đoạn thẳng AB = 5 cm.Bước 2. Dùng ê ke có góc vẽ góc BAx bằng .Bước 3. Vẽ góc ABy bằng . Ta thấy Ax và By cắt nhau tại C, ta được tam giác đều ABC.
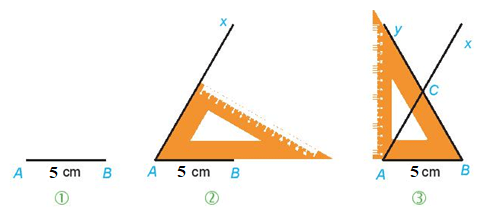b) Vẽ hình vuông ABCD có cạnh 6 cm theo hướng dẫn sau:Bước 1. Vẽ đoạn thẳng AB = 6 cm.Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Xác định điểm D trên đường thẳng đó sao cho AD = 6 cm.Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Xác định điểm C trên đường thẳng đó sao cho BC = 6 cm.Bước 4. Nối C với D ta được hình vuông ABCD
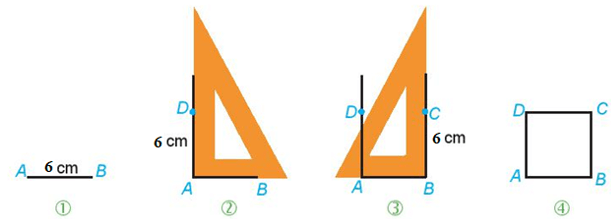c) Vẽ hình chữ nhật ABCD có một cạnh bằng 4 cm, một cạnh bằng 3 cm theo hướng dẫn sau:Bước 1. Vẽ đoạn thẳng AB = 4 cm.Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Trên đường thẳng đó lấy điểm D sao cho AD = 3 cm.Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Trên đường thẳng đó lấy điểm C sao cho BC = 3 cm.Bước 4. Nối D với C ta được hình chữ nhật ABCD.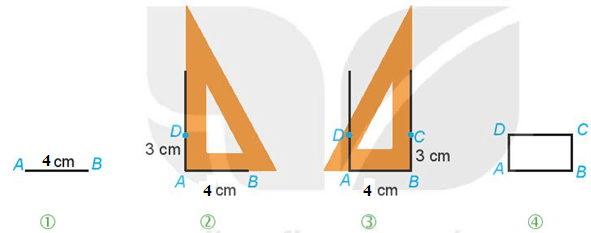
====== **** mời các bạn xem câu tiếp bên dưới **** =====