Một mảnh vườn hình chữ nhật có chiều rộng là 8m, chiều dài 9m người ta làm một lối đi xung quanh vườn rộng 2m, phần đất còn lại dùng để trồng cây. Hỏi phần đất trồng cây có diện tích là bao nhiêu?

Câu hỏi:

Một mảnh vườn hình chữ nhật có chiều rộng là 8m, chiều dài 9m người ta làm một lối đi xung quanh vườn rộng 2m, phần đất còn lại dùng để trồng cây. Hỏi phần đất trồng cây có diện tích là bao nhiêu?

A.42 m²;

B.20 m²;

Đáp án chính xác

C.18 m²;

D.26 m².

Trả lời:

Hướng dẫn giải
Đáp án đúng là: B

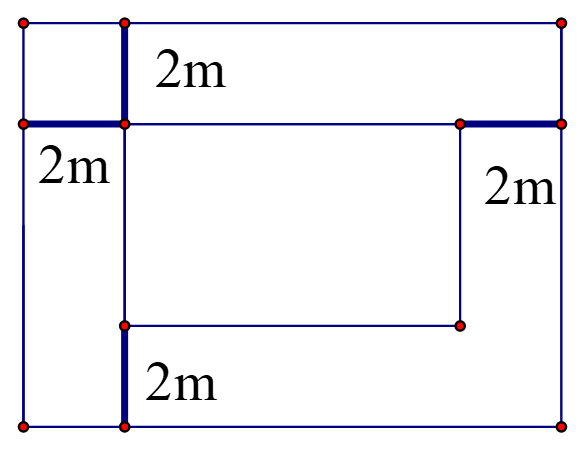
Phần đất trồng cây có chiều dài là: 9 – 2 – 2 = 5 (m)
Phần đất trồng cây có chiều rộng là: 8 – 2 – 2 = 4 (m)
Diện tích phần đất trồng cây là: 5.4 = 20 (m²)
Vậy phần đất trồng cây có diện tích là 20 m²

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Giáo án Hình chữ nhật (2023) – Toán 8

   Mời các quý thầy cô cùng tham khảo và tải về chi tiết tài liệu dưới đây:

   Giáo án Toán 8 Bài 9: Hình chữ nhật

   A. Mục tiêu

   1. Kiến thức:

   – HS nắm vững định nghĩa HCN, các tính chất của HCN, các dấu hiệu nhận biết 1 tứ giác là HCN.

   2. Kỹ năng:

   – HS biết vẽ 1 tứ giác là HCN, biết cách chứng minh 1 tứ giác là hình chữ nhật vận dụng kiến thức đó vào tam giác (tính chất trung tuyến ứng với cạnh huyền của tam giác vuông và nhận biết tam giác vuông nhờ trung tuyến)

   3. Thái độ:

   – Tích cực, tự giác, hợp tác.

   4. Phát triển năng lực:

   – Năng lực giải quyết vấn đề:  HS phân tích được tình huống học tập, phát hiện và nêu được tình huống có vấn đề, đề xuất được giải pháp giải quyết, nhận ra được sự phù hợp hay không phù hợp của giải pháp thực hiện.

   – Năng lực tính toán:  HS biết tính toán cho phù hợp.

   – Năng lực hợp tác:  HS biết hợp tác, hỗ trợ nhau trong nhóm để hoàn thành phần việc được giao ; biết nêu những mặt được và mặt thiếu sót của cá nhân và cả nhóm.

   – Chứng minhh các bất đẳng thức đơn giản

   B. Chuẩn bị

   1. Giáo viên:

   – bảng phụ ghi dấu hiệu nhận biết 1 tứ giác là HCN, compa, thước thẳng.

   2. Học sinh:

   – Compa, thước, bảng nhóm.

   C. Phương pháp

   – Vấn đáp, nêu và giải quyết vấn đề, thuyết trình, …

   D. Tiến trình dạy học

   1. Tổ chức lớp: Kiểm diện.

   2. Kiểm tra bài cũ: xen trong bài học.

   3. Bài mới

   Hoạt động của giáo viên

   Hoạt động của học sinh

   Ghi bảng

   Hoạt động 1: Khởi động
   – Treo bảng phụ, nêu câu hỏi. – Gọi một HS lên bảng trả lời. – Gọi HS khác nhận xét trước khi sang khái niệm tiếp theo … – GV đánh giá, cho điểm – GV chốt lại bằng cách nhắc lại định nghĩa, tính chất và dấu hiệu nhận biết hình thang cân, hình bình hành	– HS lên bảng trả lời câu hỏi – HS khác nhận xét hoặc nhắc lại từng khái niệm, tính chất … – HS nghe để nhớ lại định nghĩa, tính chất, dấu hiệu nhận biết hình thang cân, hình bình hành	1/ Định nghĩa hình thang cân và các tính chất của hình thang cân.   – Nêu các dấu hiệu nhận biết hình thang cân. 2/ Phát biểu định nghĩa về hình bình hành và các tính chất của hình bình hành. – Nêu các dấu hiệu nhận bếit về hình bình hành
   Hoạt động 2: Hình thành kiến thức
   – Tứ giác có 4 góc bằng nhau thì mỗi góc bằng bao nhiêu độ? Vì sao? – GV chốt lại: Tứ giác có 4 góc vuông là hình chữ nhật ⇒ Định nghĩa hình chữ nhật? – Phát biểu định nghĩa,ghi bảng – Cho HS làm ?1 – Từ  ?1 ta rút ra được nhận xét gì ?	– HS suy nghĩ trả lời: – HS suy nghĩ, phát biểu … – Phát biểu nhắc lại, ghi vào vở – Thực hiện ?1, trả lời: – HS rút ra nhận xét	1. Định nghĩa: Tứ giác ABCD là hình chữ  nhật Từ định nghĩa hình chữ nhật ta suy ra hình chữ nhật cũng là hình bình hành, cũng là một hình thang cân.
   – Hình chữ nhật vừa là hình thang cân, vừa là hình bình hành. Vậy em có thể cho biết hình chữ nhật có những tính chất nào? – GV chốt lại: Hình chữ nhật  có tất cả các tính chất của hình bình hành và hình thang cân – Từ tính chất của hình thang cân và hình bình hành ta có tính chất đặc trưng của hình chữ nhật như thế nào ?	– HS suy nghĩ, trả lời:… ● Tính chất hình thang cân: Hai đường chéo bằng nhau. ● Tính chất hình bình hành:  + Các cạnh đối bằng nhau.  + Các góc đối bằng nhau.  + Hai đường chéo cắt nhau tại trung điểm mỗi đường … – HS nhắc lại tính chất hình chữ nhật, ghi bài	2. Tính chất: – Hình chữ nhật có tất cả tính chất của hình bình hành và hình thang cân Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
   – Đưa ra bảng phụ giới thiệu các dấu hiệu nhận biết một tứ giác là hình chữ nhật. – Đây thực chất là các định lí, mỗi định lí có phần GT-KL của nó. Về nhà hãy tự ghi GT-KL và chứng minh các dấu hiệu này. Ở đây, ta chứng minh dấu hiệu 4. – Hãy viết GT-KL của dấu hiệu 4 ? – Muốn chứng minh ABCD là hình chữ nhật ta ta phải cm gì? – Giả thiết ABCD là hình bình hành cho ta biết gì? – Giả thiết hai đường chéo AC và BD bằng nhau cho ta biết thêm điều gì? – Kết hợp GT, ta có kết luận gì về tứ giác ABCD ? – GV chốt lại và ghi phần chứng minh lên bảng	– HS ghi nhận các dấu hiệu vào vở – HS đọc (nhiều lần) từng dấu hiệu – HS ghi GT-KL của dấu hiệu 4 – HS suy nghĩ trả lời:	3. Dấu hiệu nhận biết hình chữ nhật: Chứng minh
   – Treo bảng phụ vẽ hình 86 lên bảng. Cho HS là ?3 – Lần lượt nêu từng câu hỏi – Cho HS tham gia nhận xét – GV  chốt lại vấn đề … – Treo bảng phụ vẽ hình 87 lên bảng. Cho HS làm ?4 – Lần lượt nêu từng câu hỏi – Cho HS tham gia nhận xét – GV  chốt lại vấn đề …	– HS quan sát suy nghĩ Trả lời câu hỏi – HS quan sát suy nghĩ – HS quan sát, trả lời tại chỗ: – HS khác nhận xét – HS ghi định lí và nhắc lại	4. Áp dụng vào tam giác vuông:  Định lí: 1. Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh hyền. 2. Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
   Hoạt động 3: Luyện tập
   – Treo bảng phụ. Gọi HS đọc đề sau đó cho HS lên bảng điền vào ô trống – Cho HS khác nhận xét	– HS đọc đề – HS lên bảng điền vào ô trống – HS khác nhận xét	Bài 58 trang 99 SGK
   4. VẬN DỤNG
   + Nêu các định lí áp dụng vào tam giác. + Áp dụng: Giải bài tập 60 – SGK. – Cho HS nhận xét, GV cho điểm.	* Làm bài tập phần vận dụng	+ Nêu các định lí áp dụng vào tam giác. + Áp dụng định lí Py-ta-go vào tam giác vuông ABC, ta được: BC2 = 242 + 72 = 625 ⇒ BC = 25cm Vậy: AM = 12,5cm.
   5. MỞ RỘNG
   Vẽ sơ đồ tư duy khái quát nội dung bài học. Sưu tầm và làm một số bài tập nâng cao.	Làm bài tập phần mở rộng.

   4.  Hướng dẫn học sinh tự học (3p)

   – Học theo SGK. Nắm chắc các tính chất, dấu hiệu nhận biết 1 tứ giác là HCN.

   – Làm các bài tập 59; 60; 61 (tr99-SGK)—- 114; 116; 117; 118 (tr72-SBT).

   – HD 61: chứng minh AHCE là HCN, có AC = HE, AI = IC, IH = IE.

2. Giáo án Luyện tập Hình chữ nhật (2023) – Toán 8

   Mời các quý thầy cô cùng tham khảo và tải về chi tiết tài liệu dưới đây:

   Giáo án Luyện tập Toán 8 Bài 9: Hình chữ nhật

   A. Mục tiêu

   1. Kiến thức:

   – Cửng cố cho học sinh nhận biết được định nghĩa, tính chất của HCN, các dấu hiệu nhận biết HCN, tính chất đường trung tuyến ứng với cạnh huyền Tam giác vuông.

   2. Kỹ năng:

   – Biết cách áp dụng dấu hiệu nhận biết để chứng minh 1 tứ giác là HCN, vận dụng tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông để chứng minh tam giác vuông.

   3. Thái độ:

   – Tích cực, tự giác, hợp tác.

   4. Phát triển năng lực:

   – Biết vận dụng 1 cách sáng tạo tính chất đường trung tuyến trong tam giác vuông để chứng minh góc tam giác vuông.

   B. Chuẩn bị

   1. Giáo viên:

   – Bảng phụ ghi b ài tập 63 và thước thẳng.

   2. Học sinh:

   – Compa, thước, bảng nhóm.

   C. Phương pháp

   – Vấn đáp, nêu và giải quyết vấn đề, thuyết trình, …

   D. Tiến trình dạy học

   1. Tổ chức lớp: Kiểm diện.

   2. Kiểm tra bài cũ:

   – Phát biểu định nghĩa HCN? nêu các t/c về cạnh và đường chéo của HCN.

   3. Bài mới

   Hoạt động của giáo viên

   Hoạt động của học sinh

   Ghi bảng

   Hoạt động 1: Khởi động (5’)
   – Treo bảng phụ ghi đề – Gọi một HS lên bảng – Cả lớp cùng làm – Kiểm tra vở bài tập vài HS – Cho HS nhận xét câu trả lời và bài làm ở bảng – Đánh giá cho điểm – GV nhắc lại định nghĩa, tính chất của hình chữ nhật và giải thích rõ sự đúng, sai của từng câu trong câu 2	– HS đọc yêu cầu đề kiểm tra – Một HS lên bảng trả lời và làm bài (có thể vẽ hình để giải thích sự đúng sai của mỗi câu) 1/ Phát biểu như  SGK trang 97 2/ Các câu đúng: a), b), d), e) Các câu sai: c), f) – Tham gia nhận xét câu trả lời và bài làm trên bảng – Tự sửa sai (nếu có)	1/ Phát biểu định nghĩa, tính chất của hình chữ nhật.  2/ Các câu sau đúng hay sai a) Hình thang cân có một góc vuông là hình chữ nhật. b) Hình bình hành có một góc vuông là hình chữ nhật. c) Tứ giác có hai đường chéo bằng nhau là hình chữ nhật. d) Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật. e) Tứ giác có ba góc vuông là hcn f) Hình thang có hai đường chéo bằng nhau là hình chữ nhật.
   Hoạt động 2: Luyện tập (30’)
   Bài 63 trang 100 SGK – Treo bảng phụ ghi đề – Yêu cầu HS phân tích đề – Yêu cầu HS nêu GT-KL – Hướng dẫn kẻ BH ⊥ CD – Tứ giác ABHD là hình gì ?Vì sao ? – Từ đó ta có điều gì ? – Muốn tính AD ta phải tính đoạn nào ? – Muốn tính được BH ta phải làm sao ? – Trong tam giác vuông BHC ta biết được độ dài mấy đoạn ? – Áp dụng định lí Phytharo ta có điều gì ? – Vậy AD bằng ? – Gọi HS lên bảng trình bày – Cho HS khác nhận xét – GV hoàn chỉnh bài làm Bài 65 trang 100 SGK – Treo bảng phụ ghi đề – Đề bài cho ta điều gì ?     – Đề bài yêu cầu điều gì ? – Hướng dẫn vẽ hình – Yêu cầu HS nêu GT-KL – Dự đoán EFGH là hình gì ? – Khi nói tới trung điểm thì ta liên hệ đến điều gì đã học ? – EF là gì của ∆ABC ? – Ta suy ra điều gì ? – Tương tự đối với HG – Ta suy ra điều gì ? – Từ hai điều trên ta có điều gì? – Vậy EFGH là hình gì ? – EFGH còn thiếu điều kiện gì để là hình chữ nhật ? – Ta có EF // AC và AC ⊥ BD thì suy ra được điều gì ? – Mà EH như thế nào với BD ? – Ta suy ra điều gì ? – Nên góc HEF bằng ? – Vậy hình bình hành EFGH là hình gì ? – Cho HS chia nhóm. Thời gian làm bài 5’ – Cho đại diện nhóm  lên bảng trình bày – Cho HS nhóm khác nhận xét – GV hoàn chỉnh bài làm	– HS quan sát hình vẽ – HS phân tích đề – HS lên bảng nêu GT-KL – HS vẽ theo hướng dẫn của GV – ABHD là hình chữ nhật vì có 3 góc vuông – AB = DH = 10 ; AD = BH – Muốn tính AD ta phải tính được đoạn BH – Ta dựa vào định lí Phytharo vào tam giác vuông BHC – HS lên bảng trình bày lại – HS khác nhận xét – HS sửa bài vào vở – HS đọc đề và phân tích – AC ⊥ BD. E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. – EFGH là hình gì ? Vì sao ? – HS vẽ hình theo hướng dẫn – HS nêu GT-KL – EFGH là hình chữ nhật – Khi nói đến trung điểm ta liên hệ đến đường trung bình – EF là đg trung bình của ∆ABC – EF // AC và EF = ½ AC – HG là đg trung bình của∆ADC – HG // AC và HG = ½ AC – HG // EF và HG = EF – EFGH là hình bình hành – Thiếu 1 góc vuông – EFBD – EH // BD ⇒ EF ⊥ EH –  – Hình bình hành EFGH là hình chữ nhật – HS suy nghĩ cá nhân sau đó chia 4 nhóm hoạt động – Đại diện nhóm lên bảng trình bày – HS nhóm khác nhận xét – HS sửa bài vào vở	Bài 63 trang 100 SGK Tìm x trong các hình sau: Bài 65 trang 100 SGK Tứ giác ABCD có hai đường chéo vuông góc nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ? Chứng minh Ta có: E là trung điểm AB (gt)              F là trung điểm BC (gt) Nên: EF là đường trung bình của ∆ABC ⇒ EF // AC và EF = ½ AC Tương tự: HG là đường  trung bình của∆ADC ⇒ HG // AC và HG = ½ AC Do đó: HG // EF và HG = EF Nên: EFGH là hình bình hành (có 2 cạnh đối ssong và bg nhau) Ta lại có: EF // AC (cmt)                  AC ⊥ BD (gt) ⇒ EF ⊥ BD Mà EH // BD (EH là đường trung bình của ∆ABD) ⇒ EF⊥ EH Vậy: Hình bình hành EFGH là hình chữ nhật (có 1 góc vuông)
   Hoạt động 3: Vận dụng(8’)
   – Treo bảng phụ ghi đề – Cho HS lên bảng chọn – Cho HS khác nhận xét – GV hoàn chỉnh bài làm	Trắc nghiêm: 1/ Tứ giác có 3 góc vuông là hình gì ? a) Hình chữ nhật         b) Hình thang cân c) Hình bình hành       d) Tất cả đều đúng 2/ Chọn câu đúng a) Hình bình hành có hai cạnh kề bằng nhau b) Hình thang cân có hai cạnh đáy bằng nhau c) Hình thang có 1 góc vuông d) Tất cả đều đúng 3/ ∆GHK là tam giác gì ? a) Tam giác cân                  b) Tam giác vuông c) Tam giác thường            d) Tất cả đều sai
   MỞ RỘNG (2’)
   – Nêu đ/n HCN? HCN có những tính chất gì? Dấu hiệu nhận biết HCN. – Xem lại các bài đã giải – Ôn lại hình chữ nhật, hình bình hành.   /td>

   5.  Hướng dẫn học sinh tự học (3p)

   – Ôn lại đ/n đường tròn, đ/l thuận và đảo của tia phân giác của góc, tính chất đường trung trực của đoạn thẳng.

   – Làm bài tập 66(SGK).

   – Xem trước bài: đường thẳng song song với 1 đường thẳng cho trước.

3. Giải SGK Toán 8 Bài 9: Hình chữ nhật

   Giải bài tập Toán lớp 8 Bài 9: Hình chữ nhật

   Trả lời câu hỏi giữa bài

   Câu hỏi 1 trang 97 Toán 8 Tập 1: Chứng minh rằng hình chữ nhật ABCD trên hình 84 cũng là một hình bình hành, một hình thang cân.

   

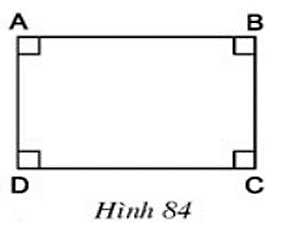
   Lời giải

   +) Hình chữ nhật ABCD có các góc đối bằng nhau (đều là góc vuông) nên ABCD là hình bình hành.

   +) Vì $AD\perp AB,AD\perp D\text{}C\Rightarrow AB//DC$

   Suy ra ABCD là hình thang

   Mặt khác, ta có: $\widehat{C}=\widehat{D}={90}^0$

   ⇒ ABCD là hình thang cân

   Câu hỏi 2 trang 98 Toán 8 Tập 1: Với một chiếc compa, ta sẽ kiểm tra được hai đoạn thẳng bằng nhau hay không bằng nhau. Bằng compa, để kiểm tra tứ giác ABCD có là hình chữ nhật hay không, ta làm thế nào ?

   Lời giải

   – Ta kiểm tra các cặp cạnh đối xem chúng có bằng nhau không

   Nếu các cặp cạnh đối bằng nhau

   ⇒ ABCD là hình bình hành

   – Sau đó: Kiểm tra hai đường chéo xem chúng bằng nhau không

   Nếu hai đường chéo bằng nhau

   ⇒ ABCD là hình chữ nhật

   Câu hỏi 3 trang 98 Toán 8 Tập 1: Cho hình 86:

   a) Tứ giác ABDC là hình gì? Vì sao?

   b) So sánh các độ dài AM và BC.

   c) Tam giác vuông ABC có AM là đường trung tuyến ứng với cạnh huyền. Hãy phát biểu tính chất tìm được ở câu b) dưới dạng một định lý.

   

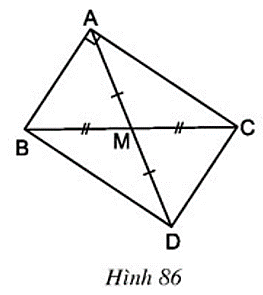
   Lời giải

   a) Tứ giác ABDC có hai đường chéo cắt nhau tại trung điểm mỗi đường

   ⇒ ABDC là hình bình hành

   Hình bình hành ABDC có góc A vuông

   ⇒ ABDC là hình chữ nhật

   b) Ta có AM = MD = $\frac{AD}{2}$ (M là trung điểm AD)

   Vì ABDC là hình chữ nhật ⇒ AD = BC (hai đường chéo)

   AM = MD =  $\frac{AD}{2}=\frac{BC}{2}.$

   Vậy $AM=\frac{BC}{2}.$

   c) Định lí được phát biểu như sau: Trong một tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền

   Câu hỏi 4 trang 98 Toán 8 Tập 1: Cho hình 87:

   a) Tứ giác ABDC là hình gì? Vì sao?

   b) Tam giác ABC là tam giác gì?

   c) Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Hãy phát biểu tính chất tìm được ở câu b) dưới dạng một định lý.

   

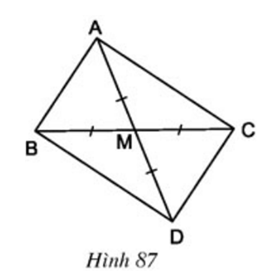
   Lời giải

   a) Tứ giác ABDC có hai đường chéo cắt nhau tại trung điểm mỗi đường

   ⇒ ABDC là hình bình hành

   Hình bình hành ABDC có hai đường chéo AD và BC bằng nhau

   ⇒ ABDC là hình chữ nhật

   b) ABDC là hình chữ nhật

   ⇒$\widehat{BAC}={90}^0$

   ⇒ ΔABC là tam giác vuông tại A

   c) Định lí: Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông

   Bài tập (trang 99, 100)

   Bài 58 trang 99 Toán 8 Tập 1: Điền vào chỗ trống, biết rằng a, b là độ dài của các cạnh, d là độ dài đường chéo của một hình chữ nhật.

   a	5	…	$\sqrt{13}$
   b	12	$\sqrt{6}$	…
   d	…	$\sqrt{10}$	7

   Lời giải:

   

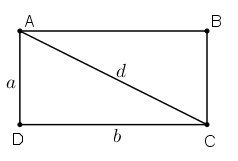
   Trong hình chữ nhật ABCD ta luôn có

    $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}={90}^0$

   Xét tam giác vuông ADC, có:

   AC² = AB² + BC²

   ⇒ d² = a² + b² (định lý Py – ta – go)

   Với a = 5, b = 12

   $\Rightarrow d^2=5^2+{12}^2\Rightarrow d=\sqrt{5^2+{12}^2}=\sqrt{169}=13$

   Với $b=\sqrt{6},d=\sqrt{10}$

   $\Rightarrow {\left(\sqrt{10}\right)}^2=a^2+{\left(\sqrt{6}\right)}^2\Rightarrow 10=a^2+6\Rightarrow a^2=10-6=4\Rightarrow a=\sqrt{4}=2$

   Với $a=\sqrt{13},d=7$

   $\Rightarrow 7^2={\left(\sqrt{10}\right)}^2+b^2\Rightarrow 49=13+b^2\Rightarrow b^2=49-13=36\Rightarrow b=\sqrt{36}=6$

   Vậy ta có bảng sau:

   a	5	2	$\sqrt{13}$
   b	12	$\sqrt{6}$	6
   d	13	$\sqrt{10}$	7

   Bài 59 trang 99 Toán 8 Tập 1: Chứng minh rằng:

   a) Giao điểm của hai đường chéo của hình chữ nhật là tâm đối xứng của hình chữ nhật đó.

   b) Hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó.

   Lời giải:

   a)

   

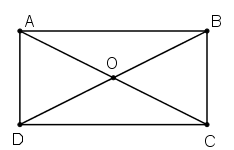
   Giả sử ABCD là hình chữ nhật. Gọi O là giao điểm của AC và BD.

   Theo tính chất đường chéo của hình chữ nhật ta có; hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.

   Vậy: OA = OC và OB = OD

   Do đó, O là tâm đối xứng của hình chữ nhật đó.

   b)

   

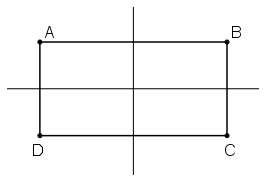
   Cách 1: Áp dung tính chất: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.

   ABCD là hình chữ nhật

   ⇒ ABCD là hình thang cân (hai đáy AB và CD)

   ⇒ Đường thẳng đi qua trung điểm AB và CD là trục đối xứng ABCD.

   Tương tự vậy: ABCD cũng là hình thang cân với hai đáy AD và BC

   ⇒ Đường thẳng đi qua trung điểm AD và BC là trục đối xứng của ABCD.

   Vậy ta có điều phải chứng minh.

   Cách 2: Sử dụng đường trung bình:

   

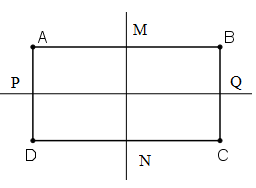
   Vì ABCD là hình chữ nhật nên ABCD là hình thang

   Ta có: M là trung điểm AB, N là trung điểm CD nên MN // AD // BC

   Mà $AD\perp AB,AD\perp CD$

   $\Rightarrow MN\perp AB,MN\perp CD$

   Suy ra MN là trung trực của AB và CD.

   Do đó A đối xứng với B qua MN, C đối xứng với D qua MN hay MN là trục đối xứng của hình chữ nhật ABCD.

   Tương tự ta có PQ cũng là trục đối xứng của hình chữ nhật ABCD.

   Bài 60 trang 99 Toán 8 Tập 1: Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có cạch góc vuông bằng 7cm và 24 cm.

   Lời giải:

   

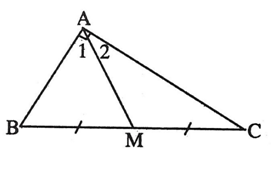
   Gọi a là độ dài cạnh huyền của tam giác vuông.

   Theo định lý Pi-ta-go ta có:

   a² = 7² + 24² = 625

   ⇒ a = 25cm

   ⇒ Độ dài trung tuyến ứng với cạnh huyền bằng: $\frac{a}{2}=\frac{25}{2}=12,5$(cm).

   Bài 61 trang 99 Toán 8 Tập 1: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AHCE là hình gì? Vì sao?

   Lời giải:

   

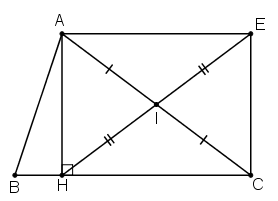
   Ta có: I là trung điểm của AC

   E đối xứng với H qua I  ⇒ IE = IH ⇒ I là trung điểm HE

   Xét tứ giác AHCE, có

   AC ∩ HE = {I} là trung điểm của AC và HE.

   ⇒ AHCE là hình bình hành (dấu hiệu nhận biết 4)

   Ta lại có : $\widehat{H}={90}^0$

   ⇒ AHCE là hình chữ nhật (đpcm).

   Bài 62 trang 99 Toán 8 Tập 1: Các câu sau đúng hay sai?

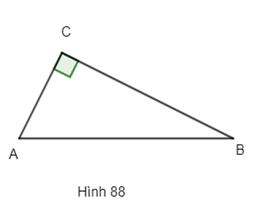
   a) Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB (h.88)

   b) Nếu điểm C thuộc đường tròn có đường kính là AB (C khác A và B) thì tam giác ABC vuông tại C (h.89).

   

   

   Lời giải:

   a) Đúng

   

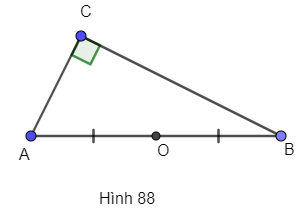
   Gọi O là trung điểm của AB.

   Ta có CO là trung tuyến ứng với cạnh huyền nên

   ⇒ $OC=\frac{AB}{2}=OA=OB$.

   A, B, C cùng thuộc đường tròn tâm O bán kính OA.

   Tâm O là trung điểm của AB nên AB là đường kính.

   Vậy C thuộc đường tròn đường kính AB.

   b) Đúng

   

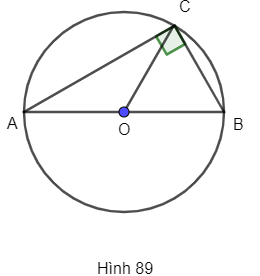
   Vì A, B, C thuộc đường tròn tâm O.

   ⇒ OA = OB = OC = R

   AB là đường kính nên AB = 2R.

   Xét tam giác ABC có:

   CO là trung tuyến và CO = $\frac{AB}{2}$.

   ⇒ ΔABC vuông tại C.

   Bài 63 trang 100 Toán 8 Tập 1: Tìm x trên hình 90

   

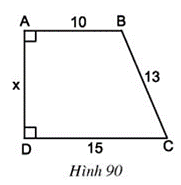
   Lời giải:

   

   * Kẻ BH vuông góc CD.

   Xét tứ giác ABHD có: $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}={90}^0$

   Suy ra tứ giác ABHD là hình chữ nhật

   $\Rightarrow$ AB = DH = 10 ( hình chữ nhật có các cạnh đối bằng nhau)

   + Suy ra: HC = DC – DH = 15 – 10 = 5

   + Xét tam giác vuông BHC có:

   BC² = BH² + HC² (định lý Py – ta – go)

   ⇔ 13² = BH² + 5²

   ⇔ BH² = 13² – 5² = 144

   ⇔ BH = 12

   + Do ABHD là hình chữ nhật nên AD = BH = 12

   Vậy x = 12.

   Bài 64 trang 100 Toán 8 Tập 1: Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.

   Lời giải:

   

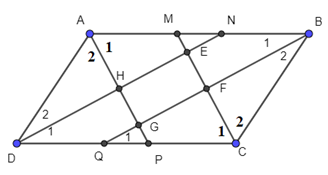
   Gọi M, N, P, Q lần lượt là giao điểm của các đường phân giác với các cạnh của hình bình hành.

   Ta có: $\widehat{D_1}=\widehat{D_2}=\frac{\widehat{ADC}}{2}$ (DN là phân giác $\widehat{ADC}$)

   $\widehat{B_1}=\widehat{B_2}=\frac{\widehat{ABC}}{2}$ (BQ là phân giác $\widehat{ABC}$)

   Mà $\widehat{ADC}=\widehat{ABC}$(hai góc đối của hình bình hành ABCD)

   $\Rightarrow \widehat{D_1}=\widehat{B_1}$

   Vì ABCD là hình bình hành AB // CD $\Rightarrow \widehat{Q_1}=\widehat{B_1}$ (hai góc so le trong)

   $\Rightarrow \widehat{D_1}=\widehat{Q_1}$

   Mà hai góc ở vị trí đồng vị

   $\Rightarrow$DN // BQ hay HE // GF

   Ta có: $\widehat{A_1}=\widehat{A_2}=\frac{\widehat{DAB}}{2}$ (AP là phân giác $\widehat{DAB}$)

   $\widehat{C_1}=\widehat{C_2}=\frac{\widehat{DCB}}{2}$ (CM là phân giác $\widehat{DCB}$)

   Mà $\widehat{DAB}=\widehat{DCB}$(hai góc đối của hình bình hành ABCD)

   $\Rightarrow \widehat{A_1}=\widehat{C_1}$

   Vì ABCD là hình bình hành AB // CD $\Rightarrow \widehat{A_1}=\widehat{QPG}$ (hai góc so le trong)

   $\Rightarrow \widehat{C_1}=\widehat{QPB}$

   $\Rightarrow$AP //DM hay GH // EF

   Xét tứ giác EFGH có:

   HE // GF (cmt)

   GH // EF (cmt)

   $\Rightarrow$EFGH là hình bình hành (1)

   Xét tam giác BFC, có:

   $\widehat{B_2}+\widehat{C_2}=\frac{\widehat{ABC}}{2}+\frac{\widehat{BCD}}{2}=\frac{\widehat{ABC}+\widehat{BCD}}{2}$

   Mà $\widehat{ABC}+\widehat{BCD}=180°$ (hai góc trong cùng phía bù nhau)

   $\Rightarrow \widehat{B_2}+\widehat{C_2}=\frac{180°}{2}=90°$

   $\Rightarrow \widehat{BFC}=180°-\left(\widehat{B_2}+\widehat{C_2}\right)=90°$ hay $\Rightarrow \widehat{EFG}=90°$(2)

   Từ (1) và (2) suy ra tứ giác EFGH là hình chữ nhật.

   Bài 65 trang 100 Toán 8 Tập 1: Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

   Lời giải:

   

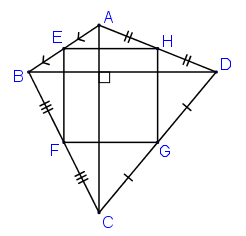
   Xét ΔABC, có:

   E là trung điểm của AB (gt)

   F là trung điểm của BC (gt)

   ⇒ EF là đường trung bình của ΔABC

   ⇒EF // AC và $\text{EF}=\frac{AC}{2}$ (1)

   Xét ΔADC, có:

   H là trung điểm của AD (gt)

   G là trung điểm của DC (gt)

   ⇒ HG là đường trung bình của ΔADC

   ⇒ HG // AC và $HG=\frac{AC}{2}$ (2)

   Từ (1) và (2) suy ra EF // HG và EF = HG

   ⇒ Tứ giác EFGH là hình bình hành (*)

   Ta có: EF // AC

   Mà $AC\perp BD$

   $\Rightarrow EF\perp BD$ (3)

   Xét ΔABD, có:

   E là trung điểm của AB

   H là trung điểm của AD

   ⇒ EH là đường trung bình của ΔABD

   ⇒ EH // BD (4)

   Từ (3) và (4) suy ra $EF\perp EH\Rightarrow \widehat{FEH}=90°$ (**)

   Từ (*) và (**) suy ra EFGH là hình chữ nhật.

   Bài 66 trang 100 Toán 8 Tập 1: Đố. Một đội công nhân đang trồng cây trên đoạn đường AB thì gặp chướng ngại vật che lấp tầm nhìn (h.92). Đội đã dựng các điểm C, D, E như trên hình vẽ rồi trồng cây tiếp trên đoạn đường EF vuông góc với DE. Vì sao AB và EF cùng nằm trên một đường thẳng?

   Lời giải:

   

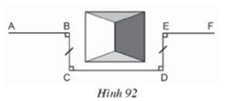
   Tứ giác BCDE có:

   BC // DE (vì cùng vuông góc với CD);

   BC = DE

   nên BCDE là hình bình hành ⇒ CD // BE (1)

   Ta có:

   $\left.\begin{array}{l}AB\perp BC\\ CD\perp BC\end{array}\right\}\Rightarrow AB//CD$ (2)

   Ta lại có:

   $\left.\begin{array}{l}\text{EF}\perp ED\\ CD\perp ED\end{array}\right\}\Rightarrow \text{EF}//CD$ (3)

   Từ (1), (2) và (3) theo tiên đề Ơ-clit suy ra A, B, E, F thẳng hàng.

4. Sách bài tập Toán 7 Bài 2 (Chân trời sáng tạo): Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

   Giải SBT Toán lớp 7 Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

   Giải trang 56 Tập 1

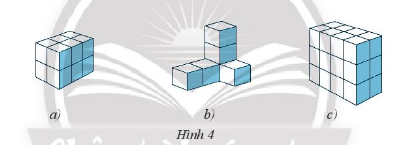
   Bài 1 trang 56 Sách bài tập Toán 7 Tập 1: Biết mỗi khối đơn vị có thể tích 1 cm³. Tính thể tích các khối trong Hình 4.

   

   Lời giải

   a) Quan sát Hình 4a), ta thấy khối hộp này được ghép bởi 12 khối đơn vị (có 2 hàng, mỗi hàng 6 khối), do đó thể tích của khối hộp là 12 cm³.

   b) Quan sát Hình 4b), ta thấy khối hộp này được ghép bởi 6 khối đơn vị, do đó thể tích của khối hộp là 6 cm³.

   c) Quan sát Hình 4c), ta thấy khối hộp này được ghép bởi 24 khối đơn vị (có 2 cột, mỗi cột 12 khối), do đó thể tích của khối hộp là 24 cm³.

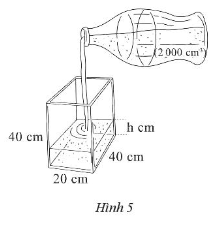
   Bài 2 trang 56 Sách bài tập Toán 7 Tập 1: Một cái bể hình hộp chữ nhật và một cái chai có kích thước và thể tích như Hình 5. Cho biết một chai nước đầy rót hết vào bể.

   a) Tính thể tích của cái bể.

   b) Tính chiều cao mực nước sau khi rót hết một chai nước vào bể.

   c) Nếu rót đầy bể thì cần bao nhiêu chai nước.

   

   Lời giải

   a) Bể nước có dạng hình hộp chữ nhật có độ dài hai cạnh đáy là 20 cm, 40 cm và chiều cao là 40 cm.

   Thể tích của bể là: V = 20 . 40 . 40 = 32 000 (cm³).

   b) Quan sát ta thấy chai nước có thể tích là 2 000 cm³ nên khi rót hết một chai nước đầy vào bể thì thể tích nước trong bể lúc này là 2 000 cm³.

   Do đó, chiều cao của mực nước sau khi rót hết một chai nước vào bể là:

   $h=\frac{2000}{20.40}=2,5$(cm).

   c) Nếu rót đầy bể thì cần số chai nước là: 32 000 : 2 000 = 16 (chai).

   Giải trang 57 Tập 1

   Bài 3 trang 57 Sách bài tập Toán 7 Tập 1: Một cái bể có kích thước như Hình 6. Bề dày bể cả bốn phía và đáy là $\frac{1}{4}$ inch.

   

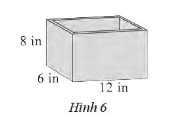
   Tính thể tích của bể.

   Lời giải

   Chiều rộng của lòng bể (không kể phần thành bể) là: $6-\frac{1}{4}-\frac{1}{4}=\frac{11}{2}$ (in).

   Chiều dài của lòng bể (không kể phần thành bể) là: $12-\frac{1}{4}-\frac{1}{4}=\frac{23}{2}$ (in).

   Chiều cao của lòng bể (không kể phần thành bể) là: $8-\frac{1}{4}=\frac{31}{4}$ (in). (do bể không có nắp nên ta chỉ cần trừ đi bề dày của phần đáy bể).

   Thể tích của bể là: V = $\frac{11}{2}.\frac{23}{2}.\frac{31}{4}=\frac{7843}{16}=490,1875$ (in³).

   Bài 4 trang 57 Sách bài tập Toán 7 Tập 1: Một bình hình lăng trụ có kích thước đáy và chiều cao như Hình 7. Nam đổ vào đó một lượng nước, rồi đo khoảng cách từ mực nước sau khi đổ tới miệng bình được 6 cm. Số lít nước đổ vào là bao nhiêu?

   

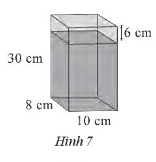
   Lời giải

   Chiều cao của mực nước đổ vào bình là: 30 – 6 = 24 (cm).

   Thể tích phần mực nước đổ vào bình là: V = 8 . 10 . 24 = 1 920 (cm³).

   Đổi: 1 920 (cm³) = 1,92 dm³ = 1,92 lít.

   Vậy số lít nước đổ vào bình là 1,92 lít.

   Bài 5 trang 57 Sách bài tập Toán 7 Tập 1: Một chiếc xe chở hàng có kích thước thùng xe là 19 ft, 8 ft và 8 ft (Hình 8) (1 fl ≈ 30,48 cm). Một thùng hàng có kích thước 2 ft, 2ft và 1 ft. Thùng xe có thể chở tối đa bao nhiêu thùng hàng nếu biết cách sắp xếp hợp lí.

   

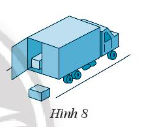
   Lời giải

   Thùng xe và thùng hàng đều có dạng hình hộp chữ nhật.

   Thể tích của thùng xe là: V = 19 . 8 . 8 = 1 216 (ft³).

   Thể tích của một thùng hàng là: v = 2 . 2 . 1 = 4 (ft³).

   Số thùng hàng có thể chở nếu biết cách sắp xếp hợp lí là: 1 216 : 4 = 304 (thùng).

   Ta có thể xếp trong thùng xe thành 8 dãy thùng hàng, mỗi dãy gồm 38 thùng hàng.

   Bài 6 trang 57 Sách bài tập Toán 7 Tập 1: Một bể cá có kích thước đáy 1 m, 0,5 m (Hình 9), chiều cao mực nước cho phép là 0,4 m. Một cái can có dung tích 10 lít, hỏi đổ bao nhiêu can nước thì tới mực nước cho phép?

   

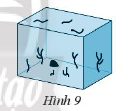
   Lời giải

   Thể tích của bể có chiều cao từ đáy tới mực nước cho phép là:

   V = 1 . 0,5 . 0,4 = 0,2 (m³).

   Đổi 0,2 m³ = 200 dm³ = 200 lít.

   Do đó, cần đổ 200 lít nước thì tới mực nước cho phép.

   Mà mỗi can có dung tích 10 lít.

   Vậy cần đổ số can nước là: 200 : 10 = 20 (can).

   Bài 7 trang 57 Sách bài tập Toán 7 Tập 1: Bạn Nam có 20 khối lập phương cạnh 4 cm (Hình 10), các khối lập phương này phải được đóng vào hộp để chuyển đi cho Khánh. Mỗi hộp có kích thước 8 cm, 10 cm, 8 cm. Phải cần bao nhiêu hộp để đóng cho đủ 20 khối lập phương trên?

   

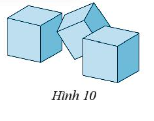
   Lời giải

   Khối lập phương có cạnh 4 cm, kích thước của hộp chứa là 8 cm, 10 cm, 8 cm.

   Do đó, khi xếp các khối lập phương vào hộp, ta chỉ xếp được tối đa 2 hàng (chồng hai khối lập phương lên nhau, chiều cao hai khối lập phương là 4 . 2 = 8 cm chính bằng chiều cao của hộp) và mỗi hàng tối đa là 4 khối, vì thế mỗi hộp chứa được tối đa 2 . 4 = 8 (khối lập phương).

   Mà 20 : 8 = 2 (dư 4).

   Vậy cần 3 chiếc hộp để chứa 20 khối lập phương.

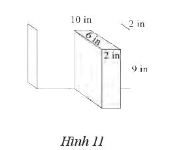
   Bài 8 trang 57 Sách bài tập Toán 7 Tập 1: Hai hình hộp chữ nhật được ghép với nhau như Hình 11.

   a) Tính thể tích của khối ghép.

   b) Tính diện tích toàn phần của khối ghép.

   

   Lời giải

   a) Khối hộp chữ nhật phía sau có kích thước 10 in, 2 in, 9 in nên có thể tích là:

   V₁ = 10 . 2 . 9 = 180 (in³).

   Khối hộp chữ nhật phía trước có kích thước 6 in, 2 in, 9 in nên có thể tích là:

   V₂ = 6 . 2 . 9 = 108 (in³).

   Hai khối hộp chữ nhật được ghép lại như Hình 11 có thể tích là:

   V = V₁ + V₂ = 180 + 108 = 288 (in³).

   b) Diện tích toàn phần của khối ghép bằng tổng diện tích toàn phần của hai khối trừ đi hai lần diện tích mặt tiếp xúc nhau.

   Diện tích toàn phần của khối hộp chữ nhật bằng tổng diện tích xung quanh và diện tích 2 đáy.

   Diện tích toàn phần của khối hộp chữ nhật phía sau là:

   S₁ = 2 . (10 + 2) . 9 + 2 . 10 . 2 = 256 (in²)

   Diện tích toàn phần của khối hộp chữ nhật phía trước là:

   S₂ = 2 . (6 + 2) . 9 + 2 . 6 . 2 = 168 (in²)

   Phần tiếp xúc nhau của hai khối hộp trên là một hình chữ nhật có kích thước là 2 in và 9 in.

   Diện tích toàn phần của khối ghép là:

   S = (S₁ + S₂) – 2 . 2 . 9 = (256 + 168) – 36 = 388 (in²).

   Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

   Bài 1: Hình hộp chữ nhật – hình lập phương

   Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

   Bài 3: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

   Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

   Bài tập cuối chương 3

5. Thắng có một sợi dây thép dài 20 cm. Thắng dùng sợi thép đó để uốn thành một hình vuông. Tính độ dài cạnh hình vuông?
   
   

   Câu hỏi:
   

   Thắng có một sợi dây thép dài 20 cm. Thắng dùng sợi thép đó để uốn thành một hình vuông. Tính độ dài cạnh hình vuông?

   Trả lời:

   Hướng dẫn giải:
   Độ dài cạnh hình vuông đó là: 20:4 = 5 (cm)
   Vậy hình vuông đó có cạnh là 5 cm.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====