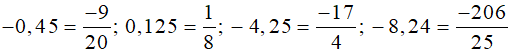Viết số thập phân 0,25 về dạng phân số ta được

Câu hỏi:

Viết số thập phân 0,25 về dạng phân số ta được

A. $\frac{1}{4}$

Đáp án chính xác

B. $\frac{5}{2}$

C. $\frac{2}{5}$

D. $\frac{1}{5}$

Trả lời:

Đáp án A$0,25=\frac{25}{100}=\frac{1}{4}$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Lý thuyết Toán lớp 6 Chương 5 (Cánh diều 2023): Phân số và số thập phân hay, chi tiết

   Lý thuyết Toán lớp 6 Chương 5 : Phân số và số thập phân

   A. Lý thuyết Chương 5 : Phân số và số thập phân

   1. Phân số với tử số và mẫu số là số nguyên

   a) Khái niệm phân số

   Kết quả của phép chia số nguyên a cho số nguyên b khác 0 có thể viết dưới dạng $\frac{a}{b}.$

   Ta gọi $\frac{a}{b}$ là phân số.

   Phân số $\frac{a}{b}$ đọc là: a phần b, a là tử số (còn gọi tắt là tử), b là mẫu số (còn gọi tắt là mẫu).

   Chú ý: Mọi số nguyên a có thể viết dưới dạng phân số là $\frac{a}{1}.$ 

   b) Phân số bằng nhau

   Khái niệm hai phân số bằng nhau: Hai phân số được gọi là bằng nhau nếu chúng cùng biểu diễn một giá trị.

   Quy tắc bằng nhau của hai phân số:

   Xét hai phân số $\frac{a}{b}$ và $\frac{c}{d}$.

   Nếu $\frac{a}{b}=\frac{c}{d}$ thì a.d = b.c. Ngược lại, nếu a.d = b.c thì $\frac{a}{b}=\frac{c}{d}$.

   Chú ý: Với a, b là hai số nguyên và b ≠ 0, ta luôn có: $\frac{a}{-b}=\frac{-a}{b}$ và $\frac{-a}{-b}=\frac{a}{b}$.

   c) Tính chất cơ bản của phân số

   * Tính chất cơ bản

   – Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.

   $\frac{a}{b}=\frac{a.m}{b.m}$ với $m\in \mathbb{Z}$, m ≠ 0.

   – Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.

   $\frac{a}{b}=\frac{a:n}{b:n}$ với m $\in$ ƯC(a, b).

   Chú ý: Mỗi phân số đều đưa được về một phân số bằng nó và có mẫu là số dương.

   * Rút gọn về phân số tối giản

   Dựa vào tính chất cơ bản của phân số, để rút gọn phân số với tử và mẫu là số nguyên về phân số tối giản ta thường làm như sau:

   Bước 1: Tìm ƯCLN của tử và mẫu sau khi đã bỏ dấu “– “ (nếu có)

   Bước 2: Chia cả tử và mẫu cho ước chung lớn nhất (ƯCLN) vừa tìm được, ta có phân số tối giản cần tìm.

   * Quy đồng mẫu nhiều phân số

   Để quy đồng nhiều phân số, ta thường làm như sau:

   Bước 1: Viết các phân số đã cho dưới dạng phân số có mẫu dương. Tìm bội chung nhỏ nhất (BCNN) của các mẫu dương đó để làm mẫu số chung.

   Bước 2: Tìm thừa số phụ của mỗi mẫu, bằng cách chia mẫu chung cho từng mẫu.

   Bước 3: Nhân tử và mẫu của mỗi phân số ở Bước 1 với thừa số phụ tương ứng.

   2. So sánh các phân số. Hỗn số dương

   a) So sánh các phân số

   * So sánh hai phân số

   Trong hai phân số khác nhau luôn có một phân số nhỏ hơn phân số kia.

   – Nếu phân số $\frac{a}{b}$ nhỏ hơn phân số $\frac{c}{d}$ thì ta viết $\frac{a}{b}<\frac{c}{d}$ hay $\frac{c}{d}>\frac{a}{b}.$  

   – Phân số lớn hơn 0 gọi là phân số dương.

   – Phân số nhỏ hơn 0 gọi là phân số âm.

   – Nếu $\frac{a}{b}<\frac{c}{d}$ và $\frac{c}{d}<\frac{e}{g}$ thì $\frac{a}{b}<\frac{e}{g}.$  

   * Cách so sánh hai phân số

   – So sánh hai phân số cùng mẫu

   Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.

   Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.

   – So sánh hai phân số không cùng mẫu

   Để so sánh hai phân số không cùng mẫu, ta quy đồng mẫu hai phân số đó (về cùng một mẫu dương) rồi so sánh các tử với nhau. Phân số nào có tử lớn hơn thì phân số đó lớn hơn.

   Bước 1: Quy đồng mẫu hai phân số đã cho (về cùng một mẫu dương)

   Bước 2: So sánh tử của các phân số: Phân số nào có tử lớn hơn thì phân số đó lớn hơn.

   b) Hỗn số dương

   Viết một phân số lớn hơn 1 thành tổng của một số nguyên dương và một phân số nhỏ hơn 1 (với tử và mẫu dương) rồi viết chúng liền nhau thì được 1 hỗn số dương.

   3. Phép cộng, phép trừ phân số.

   a) Phép cộng phân số

   * Quy tắc cộng hai phân số

   – Quy tắc cộng hai phân số cùng mẫu

   Muốn cộng hai phân số có cùng mẫu số, ta cộng tử số với nhau và giữ nguyên mẫu số.

   $\frac{a}{m}+\frac{b}{m}=\frac{a+b}{m}$

   – Quy tắc cộng hai phân số không cùng mẫu

   Muốn cộng hai phân số không cùng mẫu, ta quy đồng mẫu những phân số đó rồi cộng các tử và giữ nguyên mẫu chung.

   * Tính chất của phép cộng phân số

   Tương tự phép cộng các số tự nhiên, phép cộng phân số cũng có các tính chất: giao hoán, kết hợp, cộng với số 0.

   Trong thực hành, ta có thể sử dụng các tính chất này để tính giá trị biểu thức một cách hợp lí.

   b) Phép trừ phân số

   * Số đối của một phân số

   – Số đối của phân số $\frac{a}{b}$ kí hiệu là $-\frac{a}{b}$. Ta có: $\frac{a}{b}+\left(-\frac{a}{b}\right)=0$ 

   Chú ý: Ta có: $-\frac{a}{b}=\frac{a}{-b}=\frac{-a}{b}$ với $a,b\in \mathbb{Z},$ b ≠ 0.

   Số đối của $-\frac{a}{b}$ là $\frac{a}{b}$, tức là $-\left(-\frac{a}{b}\right)=\frac{a}{b}.$ 

   * Quy tắc trừ hai phân số

   – Muốn trừ hai phân số có cùng mẫu, ta trừ tử của số bị trừ cho tử của số trừ và giữ nguyên mẫu.

   $\frac{a}{m}-\frac{b}{m}=\frac{a-b}{m}$.

   – Muốn trừ hai phân số không cùng mẫu, ta quy đồng mẫu những phân số đó rồi trừ tử của số bị trừ cho tử của số trừ và giữ nguyên mẫu chung.

   – Muốn trừ hai phân số, ta cộng số bị trừ với số đối của số trừ:

   $\frac{a}{b}-\frac{c}{d}=\frac{a}{b}+\left(-\frac{c}{d}\right).$

   c) Quy tắc dấu ngoặc

   – Khi bỏ dấu ngoặc có dấu cộng “+” đằng trước, ta giữ nguyên dấu các số hạng trong ngoặc.

   – Khi bỏ dấu ngoặc có dấu trừ “‒“ đằng trước, ta phải đổi dấu của các số hạng trong ngoặc: dấu “+” thành dấu “‒“ và dấu “‒“ thành dấu “+”.

   $\frac{a}{b}-\left(\frac{c}{d}+\frac{e}{f}-\frac{g}{h}\right)=\frac{a}{b}-\frac{c}{d}-\frac{e}{f}+\frac{g}{h}$

   4. Phép nhân, phép chia phân số

   a) Phép nhân phân số

   * Quy tắc nhân hai phân số

   – Muốn nhân hai phân số, ta nhân các tử số với nhau và nhân các mẫu với nhau.

   $\frac{a}{b}.\frac{c}{d}=\frac{a.c}{b.d}$ với b ≠ 0 và d ≠ 0.

   – Muốn nhân một số nguyên với một phân số (hoặc nhân một phân số với một số nguyên), ta nhân số nguyên với tử của phân số và giữ nguyên mẫu của phân số đó:

   $m.\frac{a}{b}=\frac{m.a}{b};\frac{a}{b}.n=\frac{a.n}{b}$ với b ≠ 0.

   * Tính chất của phép nhân phân số

   – Tính chất giao hoán: $\frac{a}{b}.\frac{c}{d}=\frac{c}{d}.\frac{a}{b}$;

   – Tính chất kết hợp: $\left(\frac{a}{b}.\frac{c}{d}\right).\frac{p}{q}=\frac{a}{b}.\left(\frac{c}{d}.\frac{p}{q}\right)$;

   – Nhân với số 1” $\frac{a}{b}.1=1.\frac{a}{b}=\frac{a}{b}$;

   – Nhân với số 0: $\frac{a}{b}.0=0.\frac{a}{b}=0$;

   – Tính chất phân phối của phép nhân đối với phép cộng: $\frac{a}{b}.\left(\frac{c}{d}+\frac{p}{q}\right)=\frac{a}{b}.\frac{c}{d}+\frac{a}{b}.\frac{p}{q}$;

   – Tính chất phân phối của phép nhân đối với phép trừ: $\frac{a}{b}.\left(\frac{c}{d}-\frac{p}{q}\right)=\frac{a}{b}.\frac{c}{d}-\frac{a}{b}.\frac{p}{q}$.

   b) Phép chia phân số

   * Phân số nghịch đảo

   Phân số $\frac{b}{a}$ được gọi là phân số nghịch đảo của phân số $\frac{a}{b}$ với a ≠ 0 và b ≠ 0.

   Chú ý: Tích của một phân số với phân số nghịch đảo của nó thì bằng 1.

   * Phép chia phân số

   Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia:

   $\frac{a}{b}:\frac{c}{d}=\frac{a}{b}.\frac{d}{c}=\frac{a.d}{b.c}$ với b, c, d khác 0.

   c) Thứ tự thực hiện phép tính với phân số:

   * Thứ tự thực hiện phép tính với phân số trong biểu thức không chứa dấu ngoặc:

   Đối với biểu thức không chứa dấu ngoặc, ta thực hiện theo thứ tự:

   Luỹ thừa → Phép nhân và phép chia → Phép cộng và phép trừ.

   * Thứ tự thực hiện phép tính với phân số trong biểu thức có chứa dấu ngoặc:

   Đối với biểu thức có chứa dấu ngoặc, ta thực hiện theo thứ tự:

   Dấu ngoặc () → Dấu ngoặc [] → Dấu ngoặc {}.

   5. Số thập phân

   a) Số thập phân

   – Phân số thập phân là phân số mà mẫu là lũy thừa của 10 và tử là số nguyên.

   – Phân số thập phân có thể viết được dưới dạng số thập phân.

   – Số thập phân gồm hai phần:

   + Phần số nguyên được viết bên trái dấu phẩy;

   + Phần thập phân được viết bên phải dấu phẩy.

   b) So sánh các số thập phân

   * So sánh hai số thập phân

   Trong 2 số thập phân khác nhau luôn có một số nhỏ hơn số kia.

   – Nếu số thập phân a nhỏ hơn số thập phân b thì ta viết a < b hay b > a.

   – Số thập phân lớn hơn 0 gọi là số thập phân dương.

   – Số thập phân nhỏ hơn 0 gọi là số thập phân âm.

   – Nếu a < b và b < c thì a < c.

   * Cách so sánh hai số thập phân

   – So sánh hai số thập phân khác dấu:

   Số thập phân âm luôn nhỏ hơn số thập phân dương.

   – So sánh hai số thập phân dương:

   Bước 1: So sánh phần số nguyên của hai số thập phân dương đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn.

   Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng (sau dấu “,”), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữ số đó lớn hơn.

   – So sánh hai số thập phân âm:

   Nếu a < b thì ‒ a > ‒ b.

   6. Phép cộng, phép trừ số thập phân

   a) Số đối của số thập phân

   Số đối của số thập phân a kí hiệu là ‒a. Ta có: a + (‒a) = 0.

   Chú ý: Số đối của số thập phân ‒a là a, tức là ‒(‒a) = a.

   b) Phép cộng, phép trừ số thập phân

   * Cộng hai số thập phân

   – Cộng hai số thập phân dương: Muốn cộng hai số thập phân dương ta thực hiện quy tắc cộng hai số nguyên dương.

   – Cộng hai số thập phân âm: Muốn cộng hai số thập phân âm ta cộng hai số đối của chúng rồi thêm dấu “‒” đằng trước kết quả:

   (‒a) + (‒b) = ‒(a + b)

   – Cộng hai số thập phân khác dấu, ta làm như sau:

    + Nếu số dương lớn hơn hay bằng số đối của số âm thì lấy số dương trừ đi số đối của số âm.

    + Nếu số dương nhỏ hơn số đối của số âm thì ta lấy số đối của số âm trừ đi số dương rồi thêm dấu trừ “‒” trước kết quả.

   – Tính chất của phép cộng số thập phân:

   Giống như phép cộng số nguyên, phép cộng số thập phân có các tính chất giao hoán, kết hợp, cộng với số 0, cộng với số đối.

   * Trừ hai số thập phân

   – Muốn trừ hai số thập phân, ta cộng số bị trừ với số đối của số trừ.

   a – b = a + (–b)

   c) Quy tắc dấu ngoặc

   – Khi bỏ dấu ngoặc có dấu cộng “+” đằng trước, ta giữ nguyên dấu các số hạng trong ngoặc.

   – Khi bỏ dấu ngoặc có dấu trừ “‒“ đằng trước, ta phải đổi dấu của các số hạng trong ngoặc: dấu “+” thành dấu “‒“ và dấu “‒“ thành dấu “+”:

   a ‒ (b + c – d) = a ‒ b ‒ c + d

   7. Phép nhân, phép chia số thập phân

   a) Phép nhân số thập phân

   * Nhân hai số thập phân

   Muốn nhân hai số thập phân dương, ta làm như sau:

   Bước 1: Viết thừa số này ở dưới thừa số kia như đối với phép nhân các số tự nhiên

   Bước 2: Thực hiện phép nhân như nhân số tự nhiên

   Bước 3: Đếm xem trong phần thập phân ở cả hai thừa số có tất cả bao nhiêu chữ số rồi dùng dấu “,”  tách ở tích ra bấy nhiêu chữ số từ phải sang trái, ta nhận được tích cần tìm.

   Chú ý: Hai số thập phân cùng dấu thì tích là số dương; hai số thập phân khác dấu thì tích là số âm.

   Nhân hai số thập phân cùng dấu: (‒a) . (‒b) = a.b với a, b > 0

   Nhân hai số thập phân khác dấu: (‒a) . b = a.(‒b) = ‒ (a.b) với a, b > 0

   * Tính chất của phép nhân số thập phân

   Phép nhân số thập phân cũng có các tính chất như phép nhân số nguyên: giao hoán, kết hợp, nhân với số 1, phân phối của phép nhân với phép cộng và phép trừ.

   b) Phép chia số thập phân

   Muốn chia hai số thập phân dương, ta làm như sau:

   Bước 1: Số chia có bao nhiêu chữ số sau dấu “,” thì chuyển dấu “,”  ở số bị chia sang bên phải bấy nhiêu chữ số. (Khi chuyển dấu “,” ở số bị chia sang phải mà số bị chia không đủ vị trí, thì ta điền thêm những chữ số 0 vào bên phải của số đó)

   Bước 2: Bỏ đi dấu “,” ở số chia, ta nhận được số nguyên dương

   Bước 3: Đem số nhận được ở Bước 1 chia cho số nguyên dương nhận được ở Bước 2, ta có thương cần tìm.

   Chú ý: Hai số thập phân cùng dấu thì thương là số dương; hai số thập phân khác dấu thì thương là số âm.

   Chia hai số thập phân cùng dấu: (‒a) : (‒b) = a : b với a, b > 0

   Chia hai số thập phân khác dấu: (‒a) : b = a : (‒b) = ‒ (a : b) với a, b > 0

   c) Thứ tự thực hiện phép tính với số thập phân:

   * Thứ tự thực hiện phép tính với số thập phân trong biểu thức không chứa dấu ngoặc:

   Đối với biểu thức không chứa dấu ngoặc, ta thực hiện theo thứ tự:

   Luỹ thừa → Phép nhân và phép chia → Phép cộng và phép trừ.

   * Thứ tự thực hiện phép tính với số thập phân trong biểu thức có chứa dấu ngoặc:

   Đối với biểu thức có chứa dấu ngoặc, ta thực hiện theo thứ tự:

   Dấu ngoặc () → Dấu ngoặc [] → Dấu ngoặc {}.

   8. Ước lượng và làm tròn số

   a) Làm tròn số nguyên

   Để làm tròn một số nguyên (có nhiều chữ số) đến một hàng nào đó, ta làm như sau:

   – Nếu chữ số đứng ngay bên phải hàng làm tròn nhỏ hơn 5 thì ta thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0.

   – Nếu chữ số đứng ngày bên phải hàng làm tròn lớn hơn hoặc bằng 5 thì ta cộng thêm 1 vào chữ số của hàng làm tròn rồi thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0.

   Chú ý: Kí hiệu “≈” đọc là “gần bằng” hoặc “xấp xỉ”.

   b) Làm tròn số thập phân

   Để làm tròn một số thập phân dương đến một hàng nào đó (gọi là hàng làm tròn), ta làm như sau:

   – Tìm chữ số hàng làm tròn

   – Nhìn sang chữ số ngay bên phải

   + Nếu chữ số đó nhỏ hơn 5 thì giữ nguyên chữ số hàng làm tròn và thay tất cả các chữ số bên phải bằng số 0 và bỏ đi nếu chúng ở phần thập phân.

   + Nếu chữ số đó lớn hơn hay bằng 5 thì tăng chữ số hàng làm tròn thêm 1 rồi thay tất cả các chữ số bên phải bằng 0 hoặc bỏ đi nếu chũng ở phấn thập phân.

   c) Ước lượng kết quả các phép tính

   Để ước lượng kết quả các phép tính ta thực hiện làm tròn các số trong phép tính.

   9. Tỉ số. Tỉ số phần trăm

   a)Tỉ số

   * Tỉ số của hai số

   Tỉ số của a và b (b ≠ 0) là thương trong phép chia số a cho số b, kí hiệu là a : b hoặc $\frac{a}{b}$.

   Chú ý:

   – Nếu tỉ số của a và b được viết dưới dạng $\frac{a}{b}$ thì ta cũng gọi a là tử số và b là mẫu số.

   – Tỉ số của số a và số b phải được viết theo đúng thứ tự là $\frac{a}{b}$ hoặc a : b.

   – Tỉ số $\frac{a}{b}$ là phân số nếu cả tử a và mẫu b đều là số nguyên.

   * Tỉ số của hai đại lượng (cùng loại và cùng đơn vị đo)

   Tỉ số của hai đại lượng (cùng loại và cùng đơn vị đo) là tỉ số giữa hai số đo của hai đại lượng đó.

   Nhận xét: Tỉ số của hai đại lượng thể hiện độ lớn của đai lượng này so với đại lượng kia.

   a : b = $2\frac{3}{5}:\frac{9}{10}=\frac{13}{5}.\frac{10}{9}=\frac{26}{9}$.

   b) Tỉ số phần trăm

   * Tỉ số phần trăm của hai số

   – Tỉ số phần trăm của a và b là $\frac{a}{b}.100\%$.

   – Để tính tỉ số phần trăm của a và b, ta làm như sau:

   + Bước 1: Viết tỉ số $\frac{a}{b}$ 

   + Bước 2: Tính số $\frac{a.100}{b}$ và viết thêm % vào bên phải số vừa nhận được.

   Nhận xét: Có hai cách tính $\frac{a.100}{b}$ là:

   – Chia a cho b để tìm thương (ở dạng số thập phân) rồi lấy thương đó nhân với 100.

   – Nhân a với 100 rồi chia cho b, viết thương nhận được ở dạng số nguyên hoặc số thập phân.

   Chú ý: Khi tính tỉ số phần trăm của a và b mà phải làm tròn số thập phân thì ta kàn theo cách nhân a với 100 rồi chia cho b, viết thương nhận được ở dạng số nguyên hoặc số thập phân.

   * Tỉ số phần trăm của hai đại lượng (cùng loại và cùng đơn vị đo)

   Tỉ số phần trăm của hai đại lượng (cùng loại và cùng đơn vị đo) là tỉ số phần trăm giữa hai số đo của hai đại lượng đó.

   Tỉ số phần trăm của đại lượng thứ nhất có số đo (đại lượng) a và đại lượng thứ hai có số đo (đại lượng) b là: $\frac{a.100}{b}\%$.

   10. Bài toán về hai phân số

   a) Tìm giá trị phân số của một số cho trước

   – Muốn tìm giá trị $\frac{m}{n}$ của số a cho trước, ta tính $a.\frac{m}{n}$ $\left(m\in \mathbb{N},n\in \mathbb{N}*\right)$ .

   Giá trị của m% của số a là giá trị phân số $\frac{m}{100}$ của số 

   – Muốn tìm giá trị m% của số a cho trước, ta tính $a.\frac{m}{100}\left(m\in \mathbb{N}*\right)$.

   b) Tìm một số biết giá trị phân số của số đó

   – Muốn tìm một số biết $\frac{m}{n}$ của nó bằng a, ta tính $a:\frac{m}{n}\left(m,n\in \mathbb{N}*\right)$.

   – Muốn tìm một số biết m% của nó bằng a, ta tính $a:\frac{m}{100}\left(m\in \mathbb{N}*\right)$.

   B. Bài tập tự luyện

   Bài 1. Tìm số nguyên x, biết:

   a) $\frac{3}{x}=\frac{-18}{24}$;

   b) $\frac{25}{30}=\frac{2x+3}{6}$ 

   Hướng dẫn giải

   a) Vì $\frac{3}{x}=\frac{-18}{24}$

   Suy ra 3.24 = x. (–18)

   x. (–18) = 3.24

   x. (–18) = 72

   x = 72 :  (–18)

   x = –4.

   Vậy x = –4.

   b) $\frac{25}{30}=\frac{2x+3}{6}$ 

   Suy ra 30.(2x + 3) = 25.6

   30.2x + 30.3 = 150

   60x + 90 = 150

   60x = 150 – 90

   60x = 60

   x = 60 : 60

   x = 1.

   Vậy x = 1.

   Bài 2. Sắp xếp các số sau theo thứ tự tăng dần: $-\frac{2}{9};\frac{3}{4};-\frac{1}{12};\frac{5}{6};-\frac{5}{8};1\frac{1}{2}.$

   Hướng dấn giải

   Ta chia các số $-\frac{2}{9};\frac{3}{4};-\frac{1}{12};\frac{5}{6};-\frac{5}{8};1\frac{1}{2}.$ thành hai nhóm:

   Nhóm 1: gồm các số $\frac{3}{4};\frac{5}{6};1\frac{1}{2}.$

   Nhóm 2: gồm các số $-\frac{2}{9};$$-\frac{1}{12};$$-\frac{5}{8}.$

   Ta đi so sánh nhóm 1: $\frac{3}{4};\frac{5}{6};1\frac{1}{2}.$

   Có  $\frac{3}{4}=\frac{3.3}{4.3}=\frac{9}{12}$; $\frac{5}{6}=\frac{5.2}{6.2}=\frac{10}{12}$  và $1\frac{1}{2}=1+\frac{1}{2}=\frac{2}{2}+\frac{1}{2}=\frac{3}{2}=\frac{3.6}{2.6}=\frac{18}{12}.$  

   Do 9 < 10 < 18 nên $\frac{9}{12}<\frac{10}{12}<\frac{18}{12}$ 

   Vậy $\frac{3}{4}<\frac{5}{6}<1\frac{1}{2}.$ 

   Ta đi so sánh nhóm 2: $-\frac{2}{9};$$-\frac{1}{12};$$-\frac{5}{8}.$

   Vì $\frac{2}{9}<\frac{5}{9}<\frac{5}{8}$ nên $-\frac{2}{9}>-\frac{5}{8}$

   Vì $\frac{2}{9}>\frac{2}{12}>\frac{1}{12}$ nên $-\frac{2}{9}<-\frac{1}{12}$

   Do đó $-\frac{5}{8}<-\frac{2}{9}<-\frac{1}{12}$

   Trong tất cả các phân số thì phân số âm luôn nhỏ hơn phân số dương, do đó ta có:

   $-\frac{5}{8}<-\frac{2}{9}<-\frac{1}{12}<\frac{3}{4}<\frac{5}{6}<1\frac{1}{2}.$

   Vậy ta có thể sắp xếp theo thứ tự tăng dần là $-\frac{5}{8};-\frac{2}{9};-\frac{1}{12};\frac{3}{4};\frac{5}{6};1\frac{1}{2}.$

   Bài 3. Viết các đại lượng sau dưới dạng phân số và so sánh:

   a) Thời gian nào dài hơn: 2 giờ 45 phút hay $2\frac{1}{4}$ giờ?      

   b) Vận tốc nào nhỏ hơn: $\frac{5}{6}$ km/h hay $\frac{7}{9}$ km/h?

   Hướng dẫn giải

   a) Ta có 45 phút = $\frac{45}{60}$ giờ = $\frac{45:15}{60:15}$ giờ = $\frac{3}{4}$ giờ

   Do đó 2 giờ 45 phút = $\left(2+\frac{3}{4}\right)$ giờ = $\left(\frac{8}{4}+\frac{3}{4}\right)$ giờ = $\frac{11}{4}$ giờ.

   $2\frac{1}{4}$ giờ = $\left(2+\frac{1}{4}\right)$ giờ = $\left(\frac{8}{4}+\frac{1}{4}\right)$ giờ = $\frac{9}{4}$ giờ.

   Vì 11 > 9 nên $\frac{11}{4}>\frac{9}{4}$

   Do đó 2 giờ 45 phút > $2\frac{1}{4}$ giờ.

   Vậy 2 giờ 45 phút dài hơn  giờ.

   b) Ta có  $\frac{7}{9}=\frac{7.6}{9.6}=\frac{42}{54}$  và $\frac{5}{6}=\frac{5.9}{6.9}=\frac{45}{54}$

   Vì 42 < 45 nên $\frac{42}{54}<\frac{45}{54}$        

   Do đó $\frac{7}{9}$ km/h < $\frac{5}{6}$ km/h

   Vậy vận tốc $\frac{7}{9}$ km/h nhỏ hơn $\frac{5}{6}$ km/h.

   Bài 4. Tính:

   a) $\frac{6}{13}+\frac{-15}{39}$

   b) $\frac{-18}{24}+\frac{15}{21}$

   c) $\frac{1}{6}-\frac{5}{6}$

   d) $\frac{7}{21}-\frac{9}{-36}$

   Hướng dẫn giải

   a) $\frac{6}{13}+\frac{-15}{39}=\frac{6}{13}+\frac{\left(-15\right):3}{39:3}=\frac{6}{13}+\frac{-5}{13}=\frac{6+\left(-5\right)}{13}=\frac{1}{13}$

   b) $\frac{-18}{24}+\frac{15}{21}=\frac{\left(-18\right):6}{24:6}+\frac{15:3}{21:3}=\frac{-3}{4}+\frac{5}{7}$

   $=\frac{\left(-3\right).7}{4.7}+\frac{5.4}{7.4}=\frac{-21}{28}+\frac{20}{28}=\frac{\left(-21\right)+20}{28}=\frac{-1}{28}$                   

   c) $\frac{1}{6}-\frac{5}{6}=\frac{1-5}{6}=\frac{1+\left(-5\right)}{6}=\frac{-4}{6}=\frac{\left(-4\right):2}{6:2}=\frac{-2}{3}$

   d) $\frac{7}{21}-\frac{9}{-36}=\frac{7:7}{21:7}-\frac{-9}{36}=\frac{1}{3}+\left(-\frac{-9}{36}\right)=\frac{1}{3}+\frac{9}{36}$

   $=\frac{1}{3}+\frac{9:9}{36:9}=\frac{1}{3}+\frac{1}{4}=\frac{1.4}{3.4}+\frac{1.3}{4.3}$

   $=\frac{4}{12}+\frac{3}{12}=\frac{4+3}{12}=\frac{7}{12}$

   Bài 5. Tính một cách hợp lí:

   a) $A=\frac{-5}{7}+\frac{3}{4}+\frac{-1}{5}+\frac{-2}{7}+\frac{1}{4}$

   b)$B=\frac{-3}{31}-\frac{6}{17}-\frac{-1}{25}+\frac{-28}{31}+\frac{-11}{17}-\frac{1}{5}$

   c)$C=\frac{-5}{21}-\left(\frac{16}{21}-1\right)$

   Hướng dẫn giải

   a) $A=\frac{-5}{7}+\frac{3}{4}+\frac{-1}{5}+\frac{-2}{7}+\frac{1}{4}$

   $=\frac{-5}{7}+\frac{-2}{7}+\frac{3}{4}+\frac{1}{4}+\frac{-1}{5}$

    $=\left(\frac{-5}{7}+\frac{-2}{7}\right)+\left(\frac{3}{4}+\frac{1}{4}\right)+\frac{-1}{5}$    

   $=\frac{\left(-5\right)+\left(-2\right)}{7}+\frac{3+1}{4}+\frac{-1}{5}$

   $=\frac{-7}{7}+\frac{4}{4}+\frac{-1}{5}$

    $=-1+1+\frac{-1}{5}$  

   $=0+\frac{-1}{5}$

   $=\frac{-1}{5}$

   Vậy $A=\frac{-1}{5}$.

   b) $B=\frac{-3}{31}-\frac{6}{17}-\frac{-1}{25}+\frac{-28}{31}+\frac{-11}{17}-\frac{1}{5}$

   $=\frac{-3}{31}+\frac{-28}{31}-\frac{6}{17}+\frac{-11}{17}-\frac{-1}{25}-\frac{1}{5}$

   $=\left(\frac{-3}{31}+\frac{-28}{31}\right)+\left(-\frac{6}{17}+\frac{-11}{17}\right)+\left(-\frac{-1}{25}-\frac{1}{5}\right)$ 

   $=\frac{\left(-3\right)+\left(-28\right)}{31}+\frac{\left(-6\right)+\left(-11\right)}{17}+\left(\frac{1}{25}-\frac{5}{25}\right)$

   $=\frac{-31}{31}+\frac{-17}{17}+\frac{1-5}{25}$

   $=\left(-1\right)+\left(-1\right)+\frac{-4}{25}$

   $=-2+\frac{-4}{25}$

   $=\frac{-50}{25}+\frac{-4}{25}$

   $=\frac{-50+\left(-4\right)}{25}$

   $=\frac{-54}{25}.$

   Vậy $B=\frac{-54}{25}.$

   c) $C=\frac{-5}{21}-\left(\frac{16}{21}-1\right)$

   $=\frac{-5}{21}-\frac{16}{21}+1$

   $=\left(\frac{-5}{21}-\frac{16}{21}\right)+1$

   $=\frac{-5-16}{21}+1$

   $=\frac{\left(-5\right)+\left(-16\right)}{21}+1$

   $=\frac{-21}{21}+1$

   = (‒1) + 1

   = 0.

   Vậy C = 0.

   Bài 6. Hai người cùng làm chung một công việc. Nếu làm riêng, người thứ nhất phải mất 4 giờ, người thứ hai phải mất 7 giờ mới xong công việc. Hỏi nếu làm chung thì mỗi giờ cả hai người làm được mấy phần công việc?

   Hướng dẫn giải:

   Coi toàn bộ công việc là  đơn vị.

   Người thứ nhất làm xong công việc trong  giờ. Suy ra trong  giờ thì người thứ nhất làm được $\frac{1}{4}$ công việc.

   Người thứ hai làm xong công việc trong  giờ. Suy ra trong  giờ người thứ hai làm được $\frac{1}{7}$ công việc.

   Do đó trong  giờ, cả hai cùng làm thì được số phần công việc là:

   $\frac{1}{4}+\frac{1}{7}=\frac{1.7}{4.7}+\frac{1.4}{7.4}=\frac{7}{28}+\frac{4}{28}=\frac{7+4}{28}=\frac{11}{28}$ (công việc).

   Vậy nếu làm chung thì mỗi giờ cả hai người làm được $\frac{11}{28}$ công việc.

   Bài 7. Chị An sau khi tốt nghiệp đại học và đi làm, chị nhận được tháng lương đầu tiên. Chị quyết định dùng $\frac{3}{5}$ số tiền để chi tiêu cùng gia đình và $\frac{1}{3}$ số tiền để mua quà tặng bố mẹ, số tiền còn lại chị để tiết kiệm. Số phần tiền để tiết kiệm của chị An là bao nhiêu?

   Hướng dẫn giải

   Coi toàn bộ số tiền lương thág đầu tiên của chị An là 1 đơn vị.

   Số tiền còn lại sau khi chị dùng $\frac{3}{5}$ số tiền để chi tiêu cùng gia đình là:

   $1-\frac{3}{5}=\frac{5}{5}-\frac{3}{5}=\frac{5-3}{5}=\frac{2}{5}$ (số tiền)

   Số tiền để tiết kiệm của chị An là:

   $\frac{2}{5}-\frac{1}{3}=\frac{2.3}{5.3}-\frac{1.5}{3.5}=\frac{6}{15}-\frac{5}{15}=\frac{6-5}{15}=\frac{1}{15}$ (số tiền)

   Vậy số phần tiền  để tiết kiệm của chị An là $\frac{1}{15}$.

   Bài 8. Tính giá trị biểu thức (tính hợp lí nếu có thể):

   a) $\left(\frac{3}{-10}\right)\left(-\frac{-15}{2}\right)$;

   b) $\frac{-4}{7}:\frac{-1}{3};$

   c) $\frac{4}{5}+\frac{3}{5}:3-\frac{7}{8};$

   d) $\left(-\frac{5}{24}+\frac{3}{2^2}+\frac{7}{12}\right):2\frac{1}{8}$

   e) $\frac{6}{7}.\frac{8}{13}+\frac{6}{13}.\frac{9}{7}-\frac{4}{13}.\frac{6}{7}$

   Hướng dẫn giải

   a) $\left(\frac{3}{-10}\right)\left(-\frac{-15}{2}\right)=\frac{3}{-10}.\frac{15}{2}=\frac{3.15}{\left(-10\right).2}$

   $=\frac{\mathrm{3.3.5}}{\left(-2\right)\mathrm{.5.2}}=\frac{3.3}{\left(-2\right).2}=\frac{9}{-4}$;

   b) $\frac{-4}{7}:\frac{-1}{3}=\frac{-4}{7}.\frac{3}{-1}=\frac{\left(-4\right).3}{7.\left(-1\right)}=\frac{-12}{-7}=\frac{12}{7};$

   c) $\frac{4}{5}+\frac{3}{5}:3-\frac{7}{8}=\frac{4}{5}+\frac{3}{5}.\frac{1}{3}-\frac{7}{8}$

    $=\frac{4}{5}+\frac{3.1}{5.3}-\frac{7}{8}=\frac{4}{5}+\frac{1}{5}-\frac{7}{8}$  

   $=\frac{5}{5}-\frac{7}{8}$$=1-\frac{7}{8}$

   $=\frac{8}{8}-\frac{7}{8}$$=\frac{1}{8}$;

   d) $=\frac{9}{8}.\frac{8}{17}$$\left(-\frac{5}{24}+\frac{3}{2^2}+\frac{7}{12}\right):2\frac{1}{8}$

   $=\left(-\frac{5}{24}+\frac{3}{4}+\frac{7}{12}\right):\frac{17}{8}$

   $=\left(-\frac{5}{24}+\frac{18}{24}+\frac{14}{24}\right):\frac{17}{8}$

   $=\frac{-5+18+14}{24}:\frac{17}{8}$

   $=\frac{9.8}{8.17}$

   $=\frac{9}{17}$;

   e) $\frac{6}{7}.\frac{8}{13}+\frac{6}{13}.\frac{9}{7}-\frac{4}{13}.\frac{6}{7}$

   $=\frac{6}{7}.\frac{8}{13}+\frac{6}{7}.\frac{9}{13}-\frac{6}{7}.\frac{4}{13}$

   $=\frac{6}{7}.\left(\frac{8}{13}+\frac{9}{13}-\frac{4}{13}\right)$

   $=\frac{6}{7}.\frac{8+9-4}{13}$

   $=\frac{6}{7}.\frac{13}{13}$

   $=\frac{6}{7}.1$

   $=\frac{6}{7}$.

   Bài 9. Tìm x, biết:

   a) $\frac{2}{9}-\frac{7}{8}.x=1;$

   b) $\frac{5}{7}:x-1=\frac{2}{3}$;

   c) $\left(4\frac{1}{2}-2x\right).1\frac{4}{61}=6\frac{1}{2}$

   Hướng dẫn giải

   a) $\frac{2}{9}-\frac{7}{8}.x=1$

   $\frac{7}{8}.x=\frac{2}{9}-1$

   $\frac{7}{8}.x=\frac{2}{9}-\frac{9}{9}$

   $\frac{7}{8}.x=\frac{-7}{9}$

   $x=\frac{-7}{9}:\frac{7}{8}$

   $x=\frac{-7}{9}.\frac{8}{7}$

   $x=\frac{\left(-7\right).8}{9.7}$

   $x=\frac{\left(-1\right)\mathrm{.7.8}}{9.7}$

   $x=\frac{-8}{9}$

   Vậy $x=\frac{-8}{9}$

   b) $\frac{5}{7}:x-1=\frac{2}{3}$

   $\frac{5}{7}:x=\frac{2}{3}+1$

   $\frac{5}{7}:x=\frac{2}{3}+\frac{3}{3}$

   $\frac{5}{7}:x=\frac{5}{3}$

   $x=\frac{5}{7}:\frac{5}{3}$

   $x=\frac{5}{7}.\frac{3}{5}$

   $x=\frac{3}{7}.$

   Vậy $x=\frac{3}{7}.$

   c) $\left(4\frac{1}{2}-2x\right).1\frac{4}{61}=6\frac{1}{2}$

   $\left(\frac{9}{2}-2x\right).\frac{65}{61}=\frac{13}{2}$

   $\frac{9}{2}-2x=\frac{13}{2}:\frac{65}{61}$

   $\frac{9}{2}-2x=\frac{13}{2}.\frac{61}{65}$

   $\frac{9}{2}-2x=\frac{13}{2}.\frac{61}{5.13}$

   $\frac{9}{2}-2x=\frac{61}{10}$

   $2x=\frac{9}{2}-\frac{61}{10}$

   $2x=\frac{45}{10}-\frac{61}{10}$

   $2x=\frac{-16}{10}$

   $2x=\frac{-8}{5}$

   $x=\frac{-8}{5}:2$

   $x=\frac{-8}{5}.\frac{1}{2}$

   $x=\frac{-4}{5}$

   Vậy $x=\frac{-4}{5}$.

   Bài 10. Sau một thời gian gửi tiết kiệm với số tiền là 8 triệu đồng, người gửi đi rút tiền và nhận số tiền lãi bằng $\frac{1}{25}$ số tiền gửi tiết kiệm. Hỏi sau khi rút tiền thì tổng số tiền người đó nhận được là bao nhiêu?

   Hướng dẫn giải

   Vì số tiền lãi bằng $\frac{1}{25}$ số tiền gửi tiết kiệm nên số tiền lãi người đó nhận được là:

   $8 000 000.\frac{1}{25}=320 000$(đồng).

   Tổng số tiền người đó nhận được là:

   8 000 000 + 320 000 = 8 320 000 (đồng)

   Vậy tổng số tiền người đó nhận được là 8 320 000 đồng.

   Bài 11. Cho các phân số và hỗn số: $\frac{-3}{10}$; $\frac{7}{-50};$$1\frac{19}{125};$ $\frac{27}{{10}^3}$; $\frac{7}{8}.$  

   a) Viết các phân số và hỗn số trên dưới dạng phân số thập phân;

   b) Sắp xếp các số thập phân tìm được ở câu a theo thứ tự tăng dần.

   Hướng dẫn giải

   a) Ta có: $\frac{-3}{10}=-\frac{3}{10}=-0,3$;

   $\frac{7}{-50}=-\frac{7}{50}=-\frac{7.2}{50.2}=-\frac{14}{100}=-0,14$

   $1\frac{19}{125}=1+\frac{19}{125}=\frac{125}{125}+\frac{19}{125}=\frac{144}{125}=\frac{144.8}{125.8}=\frac{1152}{1000}=1,152;$

   $\frac{27}{{10}^3}=\frac{27}{1000}=0,027$

   $\frac{7}{8}=\frac{7.125}{8.125}=\frac{875}{1000}=0,875$

   Vậy $\frac{-3}{10}=-0,3;\frac{7}{-50}=-0,14;1\frac{19}{125}=1,152;\frac{27}{{10}^3}=0,027;\frac{7}{8}=0,875$

   b) Ta chia các số ‒0,3; ‒0,14; 1,152; 0,027; 0,875 thành hai nhóm:

   Nhóm 1 gồm các số: ‒0,3; ‒0,14

   Nhóm 2 gồm các số 1,152; 0,027; 0,875.

   Ta đi so sánh nhóm 1: ‒0,3; ‒0,14

   Xét hai số 0,3 và 0,14: Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số trên là hàng phần mười. Mà 3 > 1 nên 0,3 > 0,14 do đó ‒0,3 < ‒0,14.

   Ta đi so sánh nhóm 2: 1,152; 0,027; 0,875.

   Xét hai số 0,027 và 0,875: Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số này là hàng phần mười. Mà 0 < 8 nên 0,027 < 0,875.

   Xét hai số 0,875 và 1,152: Ta thấy phần nguyên của hai số là 0 < 1 nên 0,875 < 1,152.

   Suy ra 0,027 < 0,875 < 1,152

   Nhóm 1 gồm các số âm và nhóm 2 gồm các số dương. Mà số âm luôn nhỏ hơn số dương.

   Do đó ta có ‒0,3 < ‒0,14 < 0,027 < 0,875 < 1,152.

   Vậy sắp xếp các số thập phân theo thứ tự tăng dần là  ‒0,3; ‒0,14; 0,027; 0,875; 1,152.

   Bài 12. Biết nhiệt độ đông đặc của thuỷ ngân là ‒38,83°C, của rượu là ‒114,1°C, của băng phiến là 80,26°C và của nước là 0°C.

   Hãy cho biết nhiệt độ đông đặc của chất nào là thấp nhất?

   Hướng dẫn giải

   Ta so sánh hai số ‒38,83 và ‒114,1:

   Xét hai số 38,83 và 114,1 ta thấy phần nguyên của hai số là 38 < 114 nên 38,83 < 114,1 suy ra ‒38,83 > ‒114,1

   Ta thấy nhiệt độ đông đặc của thuỷ ngân (‒38,83°C) và của rượu (‒114,1°C) là số thập phân âm; nhiệt độ đông đặc của băng phiến (80,26°C ) là số thập phân dương và của nước là số 0.

   Mà số 0 luôn lớn hơn số thập phân âm và nhỏ hơn số thập phân dương.

   Do đó ta có: ‒114,1 < ‒38,83  < 0 < 80,26

   Hay ‒114,1°C < ‒38,83°C < 0°C < 80,26°C.

   Vậy nhiệt độ đông đặc của rượu là thấp nhất.

   Bài 13. Tính một cách hợp lí:

   a) A = 41,54 – 3,18 + 23,17 + 8,46 – 5,82 – 3,17

   b) B = 32,18 + 36,42 – 13,93 – (2,18 + 6,42 – 3,93)

   Hướng dẫn giải

   a) A = 41,54 – 3,18 + 23,17 + 8,46 – 5,82 – 3,17

   A = 41,54 + 8,46 + 23,17 – 3,17 – 3,18 – 5,82

   A = (41,54 + 8,46) + (23,17 – 3,17) – (3,18 + 5,82)

   A = 50 + 20 – 9

   A = 70 – 9

   A = 61.

   b) B = 32,18 + 36,42 – 13,93 – (2,18 + 6,42 – 3,93)

   B = 32,18 + 36,42 – 13,93 – 2,18 – 6,42 + 3,93

   B = (32,18 – 2,18) + (36,42 – 6,42) – (13,93 ‒ 3,93)

   B = 30 + 30 – 10

   B = 60 – 10

   B = 50.

   Bài 14. Tính (tính hợp lí nếu có thể):

   a) $-\frac{1}{13}.\left(3\frac{1}{4}-6,5\right):\frac{2}{5}+\left(-0,246\right):3$;

   b) 5,34 . 26,15 + 5,34 . (‒126,15).

   Hướng dẫn giải

   a) $-\frac{1}{13}.\left(3\frac{1}{4}-6,5\right):\frac{2}{5}+\left(-0,246\right):3$   

   $=-\frac{1}{13}.\left(\frac{13}{4}-\frac{65}{10}\right):\frac{2}{5}+\left[-\left(0,246:3\right)\right]$

   $=-\frac{1}{13}.\left(\frac{13}{4}-\frac{13}{5}\right):\frac{2}{5}+\left(-0,082\right)$

   $=-\frac{1}{13}\mathrm{.13.}\left(\frac{1}{4}-\frac{1}{5}\right):\frac{2}{5}+\left(-0,082\right)$

   $=-\frac{1}{1}\mathrm{.1.}\left(\frac{5}{20}-\frac{4}{20}\right):\frac{2}{5}+\left(-0,082\right)$

   $=-\frac{1}{20}.\frac{5}{2}+\left(-0,082\right)$

   $=-\frac{1}{4.5}.\frac{5}{2}+\left(-0,082\right)$

   $=-\frac{1}{8}+\left(-0,082\right)$

   = ‒ 0,125 + (‒0,082)

   = ‒ (0,125 + 0,082)

   = ‒ 0,207.

   b) 5,34 . 26,15 + 5,34 . (‒126,15)

   = 5,34 . [26,15 + (‒126,15)]

   = 5,34 . [‒ (126,15 – 26,15)]

   = 5,34 . (‒100)

   = ‒ (5,34 . 100)

   = ‒ 534.

   Bài 15. Mức tiêu thụ nhiên liệu của một chiếc xe máy Honda SH mode là 1,9 lít trên 100 ki – lô – mét. Giá một lít xăng E5 RON 95 – II ngày 11/04/2022 là 27 309 đồng. Một người đi xe máy đó trên quãng đường 100 km thì sẽ hết bao nhiêu tiền xăng?

   Hướng dấn giải

   Số tiền xăng người đi xe máy đi hết quãng đường 100 km là:

   27 309 . 1,9 = 51 887,1 (đồng)

   Vậy để đi được quãng đường 100 km thì người đó hết 51 887,1 đồng tiền xăng.

   Bài 16. Một khu đất hình chữ nhật có chiều dài 31,23 m và chiều rộng bằng $\frac{2}{3}$ chiều dài.

   a) Người ta lấy $\frac{5}{6}$ diện tích khu đất để đào ao. Tính diện tích ao.

   b) Diện tích còn lại người ta trồng rau. Biết cứ 1 m² thì thu hoạch được 2,1 kg rau. Hỏi người ta thu hoạch được bao nhiêu kg rau?

   c) Mỗi ki – lô – gam rau người đó bán được 12 000 đồng. Vậy nếu bán hết số rau thu hoạch được thì người đó bán được bao nhiêu tiền?

   Hướng dẫn giải

   Chiều rộng khu đất hình chữ nhật là: 31,23 . $\frac{2}{3}$ = 20,82 (m)

   Diện tích khu đất hình chữ nhật là: 31,23 . 20,82 = 650,2086 (m²)

   a) Diện tích người đó dùng để đào ao là: 650,2086 . $\frac{5}{6}$ = 541,8405 (m²).

   b) Diện tích còn lại dùng để trồng rau là: 650,2086 – 541,8405 = 108,3681 (m²)

   Số kg rau người đó thu hoạch được là: 108,3681 . 2,1 = 227, 57301 (kg).

   c) Số tiền người đó bán rau thu được là: 227,57301 . 12 000 = 2 730 876,12 (đồng).

   Bài 17. Một căn phòng hình hộp chữ nhật với chiều dài 3,8 m, chiều rộng 3,2 m và chiều cao 3 m. Người ta muốn sơn trần nhà và bốn bức tường bên trong phòng.

   a) Tính diện tích cần sơn biết tổng diện tích các cửa là 4,5 m².

   b) Biết giá tiền công sơn tường và trần nhà đều là 15 000 đồng. Tính tổng số tiền công sơn căn phòng đó.

   Hướng dẫn giải

   a) Diện tích trần nhà của căn phòng là: 3,8. 3,2 = 12,16 (m²).

   Diện tích bốn bức tường của căn phòng là: 2.(3,8 + 3,2). 3 = 42 (m²)

   Diện tích trần nhà và bốn bức tường căn phòng hình hộp chữ nhật là:

   12,16 + 42 = 54,16 (m²).

   Diện tích cần sơn là: 54,16 – 4,5 = 49,66 (m²).

   Vậy diện tích cần sơn là: 49,66 (m²).

   b) Số tiền công sơn căn phòng là:

   49,66 . 15 000 = 744 900 (đồng).

   Vậy số tiền công sơn căn phòng là 744 900 đồng.

   Bài 18. Theo https://ourworldindata.org/covid-vaccinations?country=VNM , tính đến ngày  21/03/2022, số người dân Việt Nam đã tiêm ít nhất một liều vaccine là 79 701 388 người. Sử dụng số thập phân để viết số người Việt Nam theo đơn vị triệu người. Sau đó làm tròn số thập phân đó đến:

   a) Hàng phần mười

   b) Hàng phần trăm.

   Hướng dẫn giải

   Tính đến ngày 21/03/2022, số người dân Việt Nam đã được tiêm ít nhất một liều vaccine là 79,701388 triệu người.

   a) Làm tròn số 79,701388 đến hàng phần mười:

   Do chữ số hàng phần trăm của số 79,701388 là 0 < 5 nên 79,701388 ≈ 79,7.

   Vậy số người dân Việt Nam đã được tiêm ít nhất một liều vaccine xấp xỉ 79,7 triệu người.

   b) Làm tròn số 79,701388 đến hàng phần trăm:

   Do chữ số hàng phần nghìn của số 79,701388 là 1 < 5 nên 79,701388 ≈ 79,7.

   Vậy số người dân Việt Nam đã được tiêm ít nhất một liều vaccine xấp xỉ 79,7 triệu người.

   Bài 19. Một chiếc xe máy chuyển động trên quãng đường từ Hà Nội đến Hải Phòng là 120 km. Bánh xe của chiếc xe máy có dạng hình tròn có đường kính 43 cm. Hỏi trong quá trình di chuyển từ Hà Nội đến Hải Phòng thì bánh xe quay được bao nhiêu vòng? Làm tròn kết quả đến hàng đơn vị và lấy π = 3,14.

   Hướng dẫn giải

   Đổi 120 km = 120 000 m.

   43 cm = 0,43 m.

   Chu vi của bánh xe là: C = π.d = 3,14. 0,43 = 1,3502 (m).

   Số vòng quay mà bánh xe quay được là: 120 000 : 1,3502 = 88 875,72211… (vòng)

   Làm tròn kết quả trên đến hàng đơn vị: do chữ số hàng phần mười của kết quả là 7 > 5 nên 88 875,72211…≈ 88 876.

   Vậy trong quá trình di chuyển từ Hà Nội đến Hải Phòng thì bánh xe máy quay được khoảng 88 876 vòng.

   Bài 20. Mẹ Hoa đưa cho Hoa tờ tiền 500 000 đồng để Hoa mang đi mua thức ăn cho mèo. Người bán hàng nói chỉ còn 2,45 kg thức ăn cuối cùng bán với giá 190 000 đồng một kg. Hãy ước lượng xem số tiền Hoa mang theo có đủ mua hết số thức ăn đó không?

   Hướng dẫn giải

   Hoa cần ước lượng 2,46 ≈ 2,5 kg và 190 000 ≈ 200 000.

   Sau đó thực hiện phép tính nhân: 2,5 . 200 000 = 500 000 (đồng).

   Do cả hai thừa số đều được làm tròn tăng lên nên tích đúng sẽ nhỏ hơn tích mà Hoa đã ước lượng. Vì vậy số tiền 500 000 đồng mà Hoa mang đi sẽ trả đủ cho 2,45 kg thức ăn cho mèo.

   Bài 21. Ước lượng kết quả các phép tính:

   a) 8,7 + 17,5;

   b) 24,45 – 16,67;

   c) (‒5,11) . (‒6,89);

   d) 5,39 . (4,21 +  9,89).

   Hướng dẫn giải

   a) 8,7 + 17,5 ≈ 9 + 18 = 27;

   b) 24,45 – 16,67 ≈ 24 – 17 = 7;

   c) (‒5,11) . (‒6,89) ≈ (‒5) . (‒7) = ‒ (5.7) = ‒35;

   d) 5,39 . (4,21 +  9,89) ≈ 5 . (4 + 10) = 5 . 14 = 70.

   Bài 22. Tính tỉ số của:

   a) 2 giờ và 6 giờ;

   b) 0,2 tạ và 12 kg;

   c)  m và 70 cm.

   Hướng dẫn giải

   a) Tỉ số của 2 giờ và 6 giờ là:

   2 : 6 = $\frac{2}{6}=\frac{1}{3}$.

   Vậy tỉ số của 2 giờ và 6 giờ là $\frac{1}{3}.$

   b) Đổi 0,2 tạ = 20 kg.

   Tỉ số của 20 kg và 12 kg là: $\frac{5}{3}.$

   20 : 12 = $\frac{20}{12}=\frac{5}{3}$.

   Vậy tỉ số của 0,2 tạ và 12 kg là  

   c) Đổi $\frac{3}{5}$ m = 0,6 m = 60 cm.

   Tỉ số của 60 cm và 70 cm là:

   60 : 70 =  $\frac{60}{70}=\frac{6}{7}.$

   Vậy tỉ số của $\frac{3}{5}$ m và 70 cm là $\frac{6}{7}.$

   Bài 23. Tính tỉ số phần trăm (làm tròn kết quả đến hàng phần trăm) của:

   a) 0,12 m² và 420 cm²;

   b) $\frac{2}{3}$ giờ và 12 phút.

   Hướng dẫn giải

   a) Đổi 0,12 m² = 12 cm²

   Tỉ số phần trăm của 12 cm² và 420 cm² là:  $\frac{12}{420}.100\%=\frac{12.100}{420}\%=2,\mathrm{857142\dots }\%$

   Làm tròn kết quả đến hàng phần mười: do hàng phần trăm của kết quả là 5 = 5 nên ta có 2,857142…≈ 2,9.

   Vậy tỉ số phần trăm của 0,12 m² và 420 cm² là khoảng 2,9%.

   b) Đổi $\frac{2}{3}$ giờ = 40 phút.

   Tỉ số phần trăm 40 phút và 12 phút là: $\frac{40}{12}.100\%=\frac{40.100}{12}\%=333,\mathrm{3333..}\%$

   Làm tròn kết quả đến hàng phần mười: do hàng phần trăm của kết quả là 3 < 5 nên ta có 333,33333…≈ 333,3.

   Vậy tỉ số phần trăm của $\frac{2}{3}$ giờ và 12 phút là 333,3%.

   Bài 24. Minh điều tra về loại quả ưa thích của một số bạn học sinh trong lớp, mỗi bạn trả lời một lần, được kết quả như bảng thống kê sau:

   Quả yêu thích	Cam	Ổi	Chuối	Khế	Xoài
   Số bạn chọn	6	4	3	5	7

   a) Có bao nhiêu bạn tham gia trả lời?

   b) Minh đưa ra kết luận rằng tỉ số phần trăm của số bạn thích cam và xoài so với tổng số bạn lớn hơn 50%. Minh kết luận đúng hay không?

   Hướng dẫn giải

   a) Tổng số bạn tham gia trả lời là: 6 + 4 + 3 + 5 + 7 = 25 (bạn)

   Vậy có 25 bạn tham gia trả lời.

   b) Số bạn thích quả cam và xoài là: 6 + 7 = 13 (bạn)

   Tỉ số phần trăm của số bạn thích cam và xoài so với tổng số bạn tham gia trả lời là:

   $\frac{13}{25}.100\%=\frac{13.100}{25}\%=52\%$.

   Do đó tỉ số phần trăm của số bạn thích cam và xoài so với tổng số bạn lớn hơn 50%.

   Vậy Minh đã kết luận đúng.

   Bài 25. Tính:

   a) $\frac{4}{5}$ của ‒60;

   b) 75% của 16;

   c) $\frac{1}{5}$ của 225 000 đồng;

   d) Có bao nhiêu phút trong $\frac{5}{12}$ giờ?

   Hướng dẫn giải

   a) $\frac{4}{5}$ của ‒60 là: $\left(-60\right).\frac{4}{5}=-48$;

   b) 75% của 16 là: $16.\frac{75}{100}=12$;

   c) $\frac{1}{5}$ của 225 000 đồng là: 225 000 .$\frac{1}{5}=45000$(đồng);

   d) Ta có: $\frac{5}{12}$ giờ = 60 phút

   Số phút có trong  giờ là: 60. $\frac{5}{12}$ = 25 phút.

   Bài 26. Tìm một số, biết:

   a) $\frac{3}{25}$ của nó bằng 120;

   b) 0,015 của nó bằng ‒30;

   c) 120% của nó bằng 9 lít;

   d) 6% của nó bằng 102 cây.

   Hướng dẫn giải

   a) $\frac{3}{25}$ của một số bằng 120 nên số đó là: 120 : $\frac{3}{25}=120.\frac{25}{3}=1000$;

   b) 0,015 của nó bằng ‒30 nên số đó là: (‒30) : 0,015 = ‒2 000;

   c) 120% của nó bằng 9 lít nên số đó là: 8 : $\frac{120}{100}=9.\frac{100}{120}=7,5$(lít)

   d) 6% của nó bằng 102 cây nên số đó là: 102 : $\frac{6}{100}=102.\frac{100}{6}=1700$ (cây)

   Bài 27. Nguyên liệu để muối dưa cải gồm rau cải, hành tươi, đường và muối. Khối lượng hành, đường và muối theo thứ tự bằng 5%, $\frac{1}{1000}$ và $\frac{3}{40}$ khối lượng của rau cải. Vậy nếu muối 3 kg rau cải cần bao nhiêu ki – lô – gam hành, đường và muối?

   Hướng dẫn giải

   Số ki – lô – gam hành cần là: 3.5% = $3.\frac{5}{100}=0,15$ (kg)

   Số ki – lô – gam đường cần là:$3.\frac{1}{1000}=0,003$ (kg)

   Số ki – lô – gam muối cần là: $3.\frac{3}{40}=0,225$ (kg)

   Vậy để muối 3 kg rau cải cần 0,15 kg hành; 0,003 kg đường và 0,225 kg muối.

   Bài 28. Bố Lan gửi tiết kiệm 100 triệu đồng tại một ngân hàng theo kì hạn 12 tháng với lãi suất là 0,51% một tháng (tiền lãi mỗi tháng bằng 0,51% số tiền gửi ban đầu và sau 12 tháng mới được lấy lãi).

   a) Hỏi hết thời hạn 12 tháng, bố Lan lấy cả gốc lẫn lãi được bao nhiêu?

   b) Giả sử hết kì hạn 12 tháng, bố Lan không rút gốc và lãi thì sau 1 năm nữa, bố Lan rút cả gốc lẫn lãi là bao nhiêu? Biết rằng lãi suất không thay đổi.

   Hướng dẫn giải

   Ta có $0,51\%=\frac{0,51}{100}=\frac{51}{10000}$ 

   a) Số tiền lãi nhận được sau một tháng là:

   $100000000.\frac{51}{10000}=510000$ (đồng)

   Số tiền lãi nhận được sau 12 tháng là: 510 000 . 12 = 6 120 000 (đồng)

   Số tiền cả gốc lẫn lãi bố Lan lấy được sau 1 năm là:

   100 000 000 + 6 120 000 = 106 120 000 (đồng)

   b) Số tiền lãi nhận được sau một tháng (của năm thứ hai) là:

   106 120 000 . $\frac{51}{10000}=541212$ (đồng)

   Số tiền lãi nhận được sau 12 tháng là: 541 212 . 12 = 6 494 544 (đồng)

   Số tiền cả gốc lẫn lãi bố Lan lấy được sau 2 năm là:

   106 120 000 + 6 494 544 = 112 614 544 (đồng)

   Vậy số tiền bố Lan nhận được khi lấy cả gốc lẫn lãi sau 2 năm là 112 614 544 đồng.

   Bài 29. Một cửa hàng bán chiếc xe đạp với giá khuyến mãi giảm 15% so với giá niêm yết. Biết tin khuyến mãi nên mẹ đưa Bình ra cửa hàng mua cho chiếc xe đạp với giá 7 225 000 đồng. Hỏi chiếc xe đạp có giá niêm yết là bao nhiêu?

   Hướng dẫn giải

   Vì chiếc xe đạp được giảm 15% so với giá niêm yết nên mẹ Bình đã mua chiếc xe đó bằng 85% giá niêm yết.

   Giá niêm yết của chiếc xe là:

   7 225 000 : 85% = $7225000:\frac{85}{100}=7225000.\frac{100}{85}=8500000$ (đồng)

   Vậy chiếc xe có giá niêm yết là 8 500 000 đồng.

   Bài 30. Chỉ số khối của cơ thể (Body Mass Index) viết tắt là BMI thường được sử dụng để xác định tình trạng cơ thể ở mức bình thường, suy dinh dưỡng hay béo phì. Chỉ số này tính dựa trên chiều cao và cân nặng cơ thể, giúp chúng ta có cái nhìn khách quan nhất về tình trạng cân nặng bản thân. Chỉ số BMI được tính theo công thức $BMI=\frac{m}{h^2}$ (trong đó m là khối lượng cơ thể tính theo kg, h là chiều cao cơ thể tính theo mét). Thể trạng của học sinh lớp 6 theo chỉ số BMI như sau:

    BMI < 15: Gầy;

   18 ≤ BMI < 23: Bình thường;

   23 ≤ BMI < 30:  Béo phì nhẹ;

   30 ≤ BMI < 40: Béo phì trung bình;

   40 ≤ BMI: Béo phì nặng.

   Một bạn học sinh lớp 6 cao 150 cm, nặng 45 kg, theo em tình trạng cơ thể bạn ở mức nào?

   Hướng dẫn giải

   Đổi 150 cm = 1,5 m

   Chỉ số khối của cơ thể bạn học sinh đó là: $BMI=\frac{45}{1,5^2}=\frac{45}{1,5.1,5}=\frac{45}{2,25}=20$ 

   Vì 18 ≤ BMI < 23 nên bạn học sinh đó bình thường không bị béo phì cũng không bị gầy.

   Xem thêm các bài tóm tắt lý thuyết Toán 6 Cánh diều hay, chi tiết khác:

   Lý thuyết Chương 2: Số nguyên

   Lý thuyết Chương 3: Hình học trực quan

   Lý thuyết Chương 4: Một số yếu tố thống kê và xác suất

   Lý thuyết Chương 5: Phân số và số thập phân

   Lý thuyết Chương 6: Hình học phẳng

2. Lý thuyết Số thập phân (Cánh diều 2023) hay, chi tiết | Toán lớp 6

   Lý thuyết Toán lớp 6 Bài 5: Số thập phân

   A. Lý thuyết Số thập phân

   1. Số thập phân

   – Phân số thập phân là phân số mà mẫu là lũy thừa của 10 và tử là số nguyên.

   – Phân số thập phân có thể viết được dưới dạng số thập phân.

   – Số thập phân gồm hai phần:

   + Phần số nguyên được viết bên trái dấu phẩy;

   + Phần thập phân được viết bên phải dấu phẩy.

   Ví dụ 1. Viết các phân số và hỗn số sau dưới dạng số thập phân: $\frac{-27}{100};$ $\frac{1}{25};$   $1\frac{3}{125}$.

   Hướng dẫn giải

   $\frac{-27}{100}=-0,27;$

   $\frac{1}{25}=\frac{1.4}{25.4}=\frac{4}{100}=0,04;$

   $1\frac{3}{125}=1+\frac{3}{125}=1+\frac{3.8}{125.8}=1+\frac{24}{1000}=1+0,024=1,024.$

   2. So sánh các số thập phân

   a) So sánh hai số thập phân

   Trong 2 số thập phân khác nhau luôn có một số nhỏ hơn số kia.

   – Nếu số thập phân a nhỏ hơn số thập phân b thì ta viết a < b hay b > a.

   – Số thập phân lớn hơn 0 gọi là số thập phân dương.

   – Số thập phân nhỏ hơn 0 gọi là số thập phân âm.

   
   – Nếu a < b và b < c thì a < c.

   b) Cách so sánh hai số thập phân

   * So sánh hai số thập phân khác dấu:

   Số thập phân âm luôn nhỏ hơn số thập phân dương.

   * So sánh hai số thập phân dương:

   Bước 1: So sánh phần số nguyên của hai số thập phân dương đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn.

   Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng (sau dấu “,”), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữ số đó lớn hơn.

   * So sánh hai số thập phân âm:

   Nếu a < b thì ‒ a > ‒ b.

   Ví dụ 2. Sắp xếp các số thập phân 3,124; –3,105; –3,142; 3,015 theo thứ tự giảm dần.

   Hướng dẫn giải

   Ta chia các số 3,124; –3,105; –3,142; 3,015 thành hai nhóm:

   Nhóm 1 gồm các số 3,124; 3,015.

   Nhóm 2 gồm các số –3,105; –3,142.

   Ta đi so sánh nhóm 1: 3,124; 3,015.

   Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số trên là hàng phần mười. Mà 1 > 0 nên 3,124 > 3,015.

   Ta đi so sánh nhóm 2: –3,105; –3,142.

   Xét hai số 3,105 và 3,142;

   Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số trên là hàng phần trăm. Mà 0 < 4 nên 3,105 < 3,142. Do đó –3,105 > –3,142.

   Nhóm 1 gồm các số thập phân dương, nhóm 2 gồm các số thập phân âm, mà số thập phân dương luôn lớn hơn số thập phân âm.

   Do đó 3,124 > 3,015 > –3,105 > –3,142.

   Vậy sắp xếp các số theo thứ tự giảm dần là:  3,124; 3,015; –3,105; –3,142.

   B. Bài tập tự luyện

   Bài 1. Cho các phân số và hỗn số: $\frac{-3}{10}$; $\frac{7}{-50};$ $1\frac{19}{125};$$\frac{27}{{10}^3}$; $\frac{7}{8}.$  

   a) Viết các phân số và hỗn số trên dưới dạng phân số thập phân;

   b) Sắp xếp các số thập phân tìm được ở câu a theo thứ tự tăng dần.

   Hướng dẫn giải

   a) Ta có: $\frac{-3}{10}=-\frac{3}{10}=-0,3$;

   $\frac{7}{-50}=-\frac{7}{50}=-\frac{7.2}{50.2}=-\frac{14}{100}=-0,14$

   $1\frac{19}{125}=1+\frac{19}{125}=\frac{125}{125}+\frac{19}{125}=\frac{144}{125}=\frac{144.8}{125.8}=\frac{1152}{1000}=1,152$;

   $\frac{27}{{10}^3}=\frac{27}{1000}=0,027;$

   $\frac{7}{8}=\frac{7.125}{8.125}=\frac{875}{1000}=0,875$

   Vậy $\frac{-3}{10}=-0,3;\frac{7}{-50}=-0,14;1\frac{19}{125}=1,152;\frac{27}{{10}^3}=0,027;\frac{7}{8}=0,875$

   b) Ta chia các số ‒0,3; ‒0,14; 1,152; 0,027; 0,875 thành hai nhóm:

   Nhóm 1 gồm các số: ‒0,3; ‒0,14

   Nhóm 2 gồm các số 1,152; 0,027; 0,875.

   Ta đi so sánh nhóm 1: ‒0,3; ‒0,14

   Xét hai số 0,3 và 0,14: Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số trên là hàng phần mười. Mà 3 > 1 nên 0,3 > 0,14 do đó ‒0,3 < ‒0,14.

   Ta đi so sánh nhóm 2: 1,152; 0,027; 0,875.

   Xét hai số 0,027 và 0,875: Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số này là hàng phần mười. Mà 0 < 8 nên 0,027 < 0,875.

   Xét hai số 0,875 và 1,152: Ta thấy phần nguyên của hai số là 0 < 1 nên 0,875 < 1,152.

   Suy ra 0,027 < 0,875 < 1,152

   Nhóm 1 gồm các số âm và nhóm 2 gồm các số dương. Mà số âm luôn nhỏ hơn số dương.

   Do đó ta có ‒0,3 < ‒0,14 < 0,027 < 0,875 < 1,152.

   Vậy sắp xếp các số thập phân theo thứ tự tăng dần là  ‒0,3; ‒0,14; 0,027; 0,875; 1,152.

   Bài 2. Viết các số thập phân sau dưới dạng phân số tối giản có mẫu số dương:

   ‒35,45; 0,79; ‒0,068.

   Hướng dẫn giải

   Ta có: ‒35,45 $=-\frac{3545}{100}=-\frac{3545:5}{100:5}=-\frac{709}{20}=\frac{-709}{20}$;

   0,79 $=\frac{79}{100}$;

   ‒0,068 $=-\frac{68}{1000}=-\frac{68:4}{1000:4}=-\frac{17}{250}=\frac{-17}{250}$.

   Bài 3. Biết nhiệt độ đông đặc của thuỷ ngân là ‒38,83°C, của rượu là ‒114,1°C, của băng phiến là 80,26°C và của nước là 0°C.

   Hãy cho biết nhiệt độ đông đặc của chất nào là thấp nhất?

   Hướng dẫn giải

   Ta so sánh hai số ‒38,83 và ‒114,1:

   Xét hai số 38,83 và 114,1 ta thấy phần nguyên của hai số là 38 < 114 nên 38,83 < 114,1 suy ra ‒38,83 > ‒114,1

   Ta thấy nhiệt độ đông đặc của thuỷ ngân (‒38,83°C) và của rượu (‒114,1°C) là số thập phân âm; nhiệt độ đông đặc của băng phiến (80,26°C ) là số thập phân dương và của nước là số 0.

   Mà số 0 luôn lớn hơn số thập phân âm và nhỏ hơn số thập phân dương.

   Do đó ta có: ‒114,1 < ‒38,83  < 0 < 80,26

   Hay ‒114,1°C < ‒38,83°C < 0°C < 80,26°C.

   Vậy nhiệt độ đông đặc của rượu là thấp nhất.

   Xem thêm các bài tóm tắt lý thuyết Toán 6 Cánh diều hay, chi tiết khác:

   Lý thuyết Bài 4: Phép nhân, phép chia phân số

   Lý thuyết Bài 5: Số thập phân

   Lý thuyết Bài 6: Phép cộng, phép trừ số thập phân

   Lý thuyết Bài 7: Phép nhân, phép chia số thập phân

   Lý thuyết Bài 8: Ước lượng và làm tròn số

3. Sách bài tập Toán 6 Bài 5 (Cánh diều): Số thập phân

   Giải SBT Toán lớp 6 Bài 5: Số thập phân

   Bài 53 trang 44 sách bài tập Toán lớp 6 Tập 2: Dưới đây là bảng số liệu của 5 nước châu Âu mà nam giới có chiều cao trung bình cao nhất:

   Tên nước	Phần Lan	Na Uy	Thuỵ Điển	Hà Lan	Đan Mạch
   Chiều cao (cm)	181,31	182,58	184,61	185	183,59

   (Nguồn: https://www.yan.vn)

   Đọc số liệu trên, cho biết nam giới có chiều cao trung bình cao nhất thuộc nước nào? Thấp nhất thuộc nước nào?

   Lời giải:

   Đọc bảng số liệu trên ta thấy:

   • Chiều cao trung bình của nam giới ở Phần Lan là 181,31 cm.

   • Chiều cao trung bình của nam giới ở Na Uy là 182,58 cm.

   • Chiều cao trung bình của nam giới ở Thuỵ Điển là 184,61 cm.

   • Chiều cao trung bình của nam giới ở Hà Lan là 185 cm.

   • Chiều cao trung bình của nam giới ở Đan Mạch là 183,59 cm.

   Ta có 185 > 184,61 > 183,59 > 182,58 > 181,31.

   Do đó, Hà Lan là nước có chiều cao trung bình của nam giới cao nhất với 185 cm; Phần Lan là nước có chiều cao trung bình của nam giới thấp nhất với 181,31 cm.

   Bài 54 trang 44 sách bài tập Toán lớp 6 Tập 2: Hươu cao cổ đực có chiều cao 5,8 m, cá voi xanh dài 33 m, cá mập voi dài 15 m, kì đà Kô-mô-đô dài 3,5 m, trăn mắt võng dài 10,7 m. Hãy đổi các số liệu đo độ dài trên theo đơn vị héc-tô-mét.

   Lời giải:

   Đổi: 1 m = $\frac{1}{100}$ hm = 0,01 hm.

   5,8 m = 0,058 hm.

   33 m = 0,33 hm.

   15 m = 0,15 hm.

   3,5 m = 0,035 hm.

   10,7 m = 0,107 hm.

   Bài 55 trang 44 sách bài tập Toán lớp 6 Tập 2: Viết các phân số và hỗn số sau đây dưới dạng số thập phân:

   $\frac{17}{100};\frac{-100}{1000};\frac{7}{-25};-\frac{19}{4};\frac{26}{65};\frac{45}{-250};2\frac{3}{8};\frac{36}{-400};1\frac{469}{2000}.$

   Lời giải:

   Ta viết phân số và hỗn số dưới dạng số thập phân như sau:

   $\frac{17}{100}=0,17;$

   $\frac{-100}{1000}=-0,1;$

   $\frac{7}{-25}=\frac{-28}{100}=-0,28;$

   $-\frac{19}{4}=-\frac{475}{100}=-4,75;$

   $\frac{26}{65}=\frac{2}{5}=\frac{4}{10}=0,4;$

   $\frac{45}{-250}=-\frac{9}{50}=-\frac{18}{100}=-0,18;$

   $2\frac{3}{8}=2\frac{375}{1000}=2,375;$

   $\frac{36}{-400}=-\frac{9}{100}=-0,09;$

   $1\frac{469}{2000}=1\frac{2345}{10000}=1,2345.$

   Bài 56 trang 44 sách bài tập Toán lớp 6 Tập 2: Viết các số thập phân sau dưới dạng phân số tối giản:

   – 0,475; – 0,45; 2,85; 0,31; 0,052; – 2,013; – 0,007.

   Lời giải:

   Ta viết các số thập phân dưới dạng phân số tối giản như sau:

   $–0,475=-\frac{475}{1000}=-\frac{475:25}{1000:25}=-\frac{19}{40};$

   $–0,45=-\frac{45}{100}=-\frac{45:5}{100:5}=-\frac{9}{20};$

   $2,85=\frac{285}{100}=\frac{285:5}{100:5}=\frac{57}{20};$

   $0,31=\frac{31}{100};$

   $0,052=\frac{52}{1000}=\frac{52:4}{1000:4}=\frac{13}{250};$

   $–2,013=-\frac{2013}{1000};$

   $–0,007=-\frac{7}{1000}$.

   Bài 57 trang 44 sách bài tập Toán lớp 6 Tập 2: Tìm điều kiện của số tự nhiên n để phân số $\frac{n+2}{300}$ viết được dưới dạng phân số thập phân.

   Lời giải:

   Ta có $\frac{n+2}{300}=\frac{n+2}{3.100}$ nên $\frac{n+2}{300}$ viết được thành phân số thập phân nếu (n+2) ⋮ 3

   Suy ra n + 2 = 3k hay n=3k – 2, k ∈ ℕ*.

   Thử lại với n=3k – 2, k ∈ ℕ* ta có:

   $\frac{n+2}{300}=\frac{3k-2+2}{300}=\frac{3k}{300}=\frac{k}{100}$

   Khi đó $\frac{n+2}{300}$viết được thành phân số thập phân.

   Vậy n=3k – 2, k ∈ ℕ*.

   Bài 58 trang 44 sách bài tập Toán lớp 6 Tập 2: Sao Thuỷ có bề mặt rất giống với bề mặt của Mặt Trăng và có khối lượng nặng bằng 0,055 lần Trái Đất; Sao Kim có khí quyển nóng bỏng với khối lượng nặng bằng 0,816 lần Trái Đất. Hãy viết các số thập phân trên dưới dạng phân số tối giản.

   Lời giải:

   Ta viết các số thập phân dưới dạng phân số tối giản như sau:

   $0,055=\frac{55}{1000}=\frac{55:5}{1000:5}=\frac{11}{200};$

   $0,816=\frac{816}{1000}=\frac{816:8}{1000:8}=\frac{102}{125}$.

   Bài 59 trang 44 sách bài tập Toán lớp 6 Tập 2: Viết các số sau theo thứ tự tăng dần:

   a) 8,017; 8,107; 8,710; 8,01;

   b) 23,049; – 23,051; – 23,105; – 23,150;

   c) – 13,5; 3,5; – 2,995; – 7,65;

   d) – 0,7; – 0,696; 0,69; 0,609.

   Lời giải:

   a) 8,017; 8,107; 8,710; 8,01

   Ta thấy các số đều có phần nguyên là 8.

   Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần mười. Do 0 < 1 < 7 nên 8,017 < 8,107 < 8,710 và 8,01 < 8,107 < 8,710.

   Xét hai số thập phân 8,017 và 8,01 = 8,010.

   Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần nghìn. Do 0 < 7 nên 8,010 < 8,017 hay 8,01 < 8,017.

   Vậy viết các số theo thứ tự tăng dần là: 8,01; 8,017; 8,107; 8,710.

   b) 23,049; – 23,051; – 23,105; – 23,150

   Xét ba số thập phân: 23,051; 23,105;23,150.

   Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần mười. Do 0 < 1 nên 23,051 < 23,105 và 23,051 < 23,150.

   Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau của hai số thập phân 23,105 và 23,150 là cặp chữ số ở vị trí hàng phần trăm. Do 0 < 5 nên 23,105 < 23,150.

   Suy ra 23,051 < 23,105 < 23,150.

   Nên – 23,051 >– 23,105 > – 23,150.

   Mà số thập phân âm luôn nhỏ hơn số thập phân dương nên ta có:

   – 23,150 < – 23,105 < – 23,051 < 23,049.

   Vậy viết các số theo thứ tự tăng dần là: – 23,150;– 23,105; – 23,051; 23,049.

   c) – 13,5; 3,5; – 2,995; – 7,65

   Xét ba số thập phân: 13,5;2,995; 7,65.

   Do 13 > 7 > 2 nên 13,5 > 7,65 > 2,995.

   Do đó – 13,5 < – 7,65 < – 2,995.

   Mà số thập phân âm luôn nhỏ hơn số thập phân dương nên ta có:

   – 13,5 < – 7,65 < – 2,995 < 3,5.

   Vậy viết các số theo thứ tự tăng dần là: – 13,5; – 7,65; – 2,995; 3,5.

   d) – 0,7; – 0,696; 0,69; 0,609

   Ta chia các số thập phân trên thành hai nhóm:

   • Nhóm 1: gồm hai số thập phân âm – 0,7; – 0,696.

   • Nhóm 2: gồm hai số thập phân dương 0,69; 0,609.

   + So sánh nhóm 1: – 0,7 và– 0,696.

   Xét hai số thập phân 0,7 và 0,696.

   Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần mười. Do 7 > 6 nên 0,7 > 0,696.

   Do đó – 0,7 <– 0,696.

   + So sánh nhóm 2: 0,69 và 0,609.

   Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần trăm. Do 0 < 9 nên 0,609 < 0,69.

   Mà số thập phân âm luôn nhỏ hơn số thập phân dương nên ta có:

   – 0,7 <– 0,696 < 0,609 < 0,69.

   Vậy viết các số theo thứ tự tăng dần là: – 0,7;– 0,696; 0,609; 0,69.

   Bài 60 trang 45 sách bài tập Toán lớp 6 Tập 2: Bốn bạn Đức, Trung, Kiên, Nguyên cùng đo chiều cao. Đức cao 1,39 m, Trung cao 1 320 mm, Kiên cao một mét rưỡi, Nguyên cao 1 m 390 mm.

   a) Bạn nào cao nhất, bạn nào thấp nhất?

   b) Những bạn nào có chiều cao bằng nhau?

   Lời giải:

   Ta có:

   Bạn Đức cao 1,39 m = 1 390 mm.

   Bạn Trung cao1 320 mm.

   Bạn Kiên cao một mét rưỡi tức là 1,5 m = 1 500 mm.

   Bạn Nguyên cao1 m 390 mm = 1 390 mm.

   Ta có 1 320 mm < 1 390 mm < 1 500 mm.

   a) Bạn Kiên cao nhất (1 500 mm), bạn Trung thấp nhất (1 320 mm).

   b) Bạn Đức và bạn Nguyêncó chiều cao bằng nhau (cùng bằng 1 390 mm).

   Bài 61 trang 45 sách bài tập Toán lớp 6 Tập 2: Chất xơ là một thành phần rất quan trọng trong bữa ăn hằng ngày. Hãy sắp xếp các món ăn trong bảng dưới đây theo thứ tự lượng chất xơ tăng dần.

   

   Lời giải:

   Ta có 0,44 g < 0,52 g < 0,65 g < 0,9 g < 3,01 g < 3,57 g.

   Do đó sắp xếp các món ăn theo thứ tự lượng chất xơ tăng dần là: 1 đĩa cơm sườn, 1 bát canh bí đao, 1 đĩa lạc rang, 1 đĩa khoai tây, 1 cốc chè nhãn, 1 đĩa chuối sấy.

   Bài 62 trang 45 sách bài tập Toán lớp 6 Tập 2:

   1) Tìm số tự nhiên x lớn nhất, biết:

   a) x < 3,005; b) x < $\frac{157}{100}$.

   2) Tìm số tự nhiên y bé nhất, biết:

   a) y > 9,999; b) y > $\frac{2021}{1000}$.

   Lời giải:

   1) Tìm số tự nhiên x lớn nhất

   a) Ta có x < 3,005

   Vì x là số tự nhiên nên suy ra x ≤ 3.

   Do đó x ∈ {0; 1; 2; 3}.

   Mà x là số tự nhiên lớn nhất nên x = 3.

   Vậy số tự nhiên lớn nhất cần tìm là x = 3.

   b) Ta có x < $\frac{157}{100}$ = 1,57.

   Vì x là số tự nhiên nên suy ra x ≤ 1.

   Do đó x ∈ {0; 1}.

   Mà x là số tự nhiên lớn nhất nên x = 1.

   Vậy số tự nhiên lớn nhất cần tìm là x = 1.

   2) Tìm số tự nhiên y bé nhất:

   a) Ta có y > 9,999

   Vì y là số tự nhiên nên suy ra y ≥ 10.

   Do đó y ∈ {10; 11; …}.

   Mà y là số tự nhiên bé nhất nên y = 10.

   Vậy số tự nhiên bé nhất cần tìm là y = 10.

   b) Ta có y > $\frac{2021}{1000}$> = 2,021.

   Vì y là số tự nhiên nên suy ra y ≥ 3.

   Do đó y ∈ {3; 4; …}.

   Mà y là số tự nhiên bé nhất nên y = 3.

   Vậy số tự nhiên bé nhất cần tìm là y = 3.

   Bài 63 trang 45 sách bài tập Toán lớp 6 Tập 2: Tìm hai số tự nhiên liên tiếp m vàn, biết:

   a) m < 16,2756<n;

   b) n <9,2995<m.

   Lời giải:

   a) m < 16,2756<n

   Do m và n là các số tự nhiên nên ta có m ≤ 16 và n ≥ 17.

   Mà m và n là hai số tự nhiên liên tiếp nên m = 16 và n = 17.

   Vậy m = 16 và n = 17.

   b) n <9,2995<m.

   Do m và n là các số tự nhiên nên ta có n ≤ 9 và m ≥ 10.

   Mà m và n là hai số tự nhiên liên tiếp nên n = 9 và m = 10.

   Vậy m = 10 và n = 9.

   Bài 64 trang 45 sách bài tập Toán lớp 6 Tập 2: Cho x

   Lời giải:

   Ta có b< 1,25 và b là số tự nhiên nên b ∈ {0; 1}.

   Với b = 0 thì x < 0, khi đó x không thỏa mãn là số tự nhiên. Ta loại trường hợp này.

   Với b = 1 thì x < 1, khi đó số tự nhiên x thỏa mãn là x = 0.

   Vậy x = 0.

   Bài 65 trang 45 sách bài tập Toán lớp 6 Tập 2:

   a) Tìm các số thập phân x có một chữ số ở phần thập phân sao cho: 8<x<9.

   b) Tìm các số thập phân x có hai chữ số ở phần thập phân sao cho: 0,1<x<0,2.

   Lời giải:

   a) Các số thập phân x có một chữ số ở phần thập phân sao cho 8<x<9 là:

   x ∈ {8,1; 8,2; 8,3; 8,4; 8,5; 8,6; 8,7; 8,8; 8,9}.

   b) Các số thập phân x có hai chữ số ở phần thập phân sao cho 0,1<x<0,2 là:

   x ∈ {0,11; 0,12; 0,13; 0,14; 0,15; 0,16; 0,17; 0,18; 0,19}.

4. Lý thuyết Số thập phân (Chân trời sáng tạo 2023) hay, chi tiết | Toán lớp 6

   Lý thuyết Toán lớp 6 Bài 1: Số thập phân

   Video giải Toán 6 Bài 1: Số thập phân – Chân trời sáng tạo

   A. Lý thuyết Số thập phân

   1. Số thập phân âm

   – Phân số thập phân là phân số có mẫu số là lũy thừa của 10.

   Ví dụ 1. Các phân số 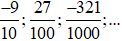 là các phân số thập phân.

   – Các phân số thập phân dương được viết dưới dạng số thập phân dương.

   – Các phân số thập phân âm được viết dưới dạng số thập phân âm.

   Ví dụ 2.

   0,332; 12,412 là các số thập phân dương.

   −3,712; −4,15 là các số thập phân âm.

   Số thập phân gồm hai phần:

   – Phần số nguyên viết bên trái dấu phẩy;

   – Phần thập phân viết bên phải dấu phẩy.

   Ví dụ 3. 

   – Số 42,25 là số thập phân dương có phần số nguyên là 42 và phần thập phân là 25.

   – Số −12,316 là số thập phân âm có phần số nguyên là −12 và phần thập phân là 316.

   2. Số đối của một số thập phân

   Hai số thập phân gọi là đối nhau khi chúng biểu diễn hai phân số thập phân đối nhau.

   Ví dụ 4. 

   – Số đối của 3,45 là −3,45;

   – Số đối của −2,36 là 2,36.

   3. So sánh hai số thập phân

   – Nếu hai số thập phân trái dấu, số thập phân dương lớn hơn số thập phân âm.

   – Trong hai số thập phân âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.

   Ví dụ 5. Sắp xếp các số thập phân theo thứ tự tăng dần:

   −16,25; 8,36; −21,4; 7,24.

   Lời giải:

   Để sắp xếp các số thập phân sau theo thứ tự tăng dần, ta thực hiện:

   Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.

   Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:

   – Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.

   – Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.

   Sắp xếp các số thập phân sau theo thứ tự tăng dần:

   * Phân loại:

   – Nhóm các số thập phân dương: 8,36; 7,24.

   –  Nhóm các số thập phân âm: −16,25; −21,4.

   * So sánh các số thập phân trong theo nhóm: 

   – Nhóm các số thập phân dương: ta so sánh phần nguyên của các số trên, vì 8 > 7 nên 8,36 > 7,24.

   –  Nhóm các số thập phân âm: Số đối của các số −16,25; −21,4 lần lượt là 16,25; 21,4.

   Ta so sánh phần nguyên của hai số 16,25 và 21,4, vì 16 < 21 nên 16,25 < 21,4.

   Hay −16,25 > −21,4.

   Do đó −21,4 < −16,25 < 7,24 < 8,36.

   Vậy các số được sắp xếp thứ tự tăng dần là: −21,4; −16,25; 7,24; 8,36.

   B. Bài tập tự luyện

   Bài 1. Viết các phân số sau dưới dạng số thập phân:

   

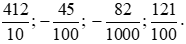
   Lời giải: 

   Các phân số trên đều là phân số thập phân.

   Cách đổi các phân số thập phân sang số thập phân thì ta quy về bài toán chia một số cho 10; 100; 1 000 (kết quả để dưới dạng số thập phân).

   Quy tắc: Muốn chia một số cho 10; 100; 1 000 ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.

   Đổi lần lượt các phân số thập phân trên ra số thập phân, ta được:

   

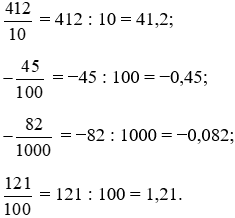
   Bài 2. Viết các số thập phân sau đây dưới dạng phân số thập phân:

   −14,5; 25,12; −32,46; −0,785.

   Lời giải:

   – Các phân số thập phân được viết dưới dạng số thập phân.

   – Số các chữ số thập phân bằng đúng số các chữ số 0 ở mẫu của phân số thập phân.

   Đổi lần lượt các số thập phân trên ra phân số thập phân, ta được:

   

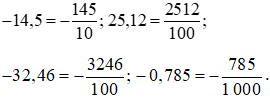
   Bài 3. Tìm số đối của các số thập phân sau:

   34,18; −26,8; −0,465; 2,4.

   Lời giải:

   Cách tìm số đối của một số thập phân: ta thêm dấu trừ vào trước số thập phân đó.

   Số đối của 34,18 là −34,18;

   Số đối của −26,8 là −(−26,8) hay 26,8;

   Số đối của −0,465 là −(−0,465) = 0,465;

   Số đối của 2,4 là −2,4.

   Bài 4: Hãy sắp xếp các số sau theo thứ tự giảm dần:

   0,6; −24,45; −24,15; 35,18; 21,75.

   Lời giải: 

   Để sắp xếp các số thập phân sau theo thứ tự giảm dần, ta làm như sau:

   Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.

   Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:

   – Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.

   – Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.

   Sắp xếp các số thập phân sau theo thứ tự giảm dần:

   * Phân loại:

   – Nhóm các số thập phân dương: 0,6; 35,18; 21,75.

   – Nhóm các số thập phân âm: −24,45; −24,15.

   * So sánh các số thập phân trong theo nhóm: 

   – Nhóm các số thập phân dương: ta so sánh phần nguyên của các số trên.

   Vì 35 > 21 > 0 nên 35,18 > 21,75 > 0,6.

   –  Nhóm các số thập phân âm: Số đối của các số −24,45; −24,15 lần lượt là 24,45; 24,15.

   + Phần nguyên của hai số 24,45; 24,15 đều là 24.

   + Ta so sánh phần thập phân của hai số. Hàng phần mười của số 24,45; 24,15 lần lượt là 4 và 1.

   Vì 1 < 4 nên 24,15 < 24,45, hay −24,15 > −24,45.

   Do đó 35,18 > 21,75 > 0,6 > −24,15 > −24,45.

   Vậy các số được sắp xếp thứ tự giảm dần là: 35,18; 21,75; 0,6; −24,15; −24,45.

   Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:

   Lý thuyết Bài 7: Hỗn số

   Lý thuyết Bài 1: Số thập phân

   Lý thuyết Bài 2: Các phép tính với số thập phân

   Lý thuyết Bài 3: Làm tròn số thập phân và ước lượng kết quả

   Lý thuyết Bài 4: Tỉ số và tỉ số phần trăm

5. Sách bài tập Toán 6 Bài 1 (Chân trời sáng tạo): Số thập phân

   Giải SBT Toán lớp 6 Bài 1: Số thập phân

   Bài 1 trang 47 sách bài tập Toán lớp 6 Tập 2: Viết các phân số thập phân sau đây dưới dạng số thập phân:

   .

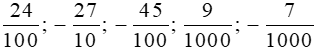   Lời giải:

   Cách đổi các phân số thập phân sang số thập phân thì ta quy về bài toán chia một số cho 10; 100; 1 000 (kết quả để dưới dạng số thập phân).

   Quy tắc: Muốn chia một số cho 10; 100; 1 000 ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.

   Đổi lần lượt các phân số thập phân trên ra số thập phân, ta được:

   

   Bài 2 trang 47 sách bài tập Toán lớp 6 Tập 2: Viết các số thập phân sau đây dưới dạng phân số thập phân:

   0,15; −0,005; −0,04; 0,008; −0,4.

   Lời giải:

   – Các phân số thập phân được viết dưới dạng số thập phân.

   – Số các chữ số thập phân bằng đúng số các chữ số 0 ở mẫu của phân số thập phân.

   Đổi lần lượt các số thập phân trên ra phân số thập phân, ta được:

   

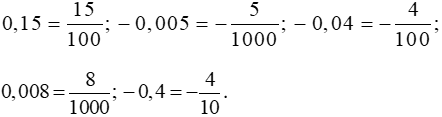
   Bài 3 trang 48 sách bài tập Toán lớp 6 Tập 2: Tìm số đối của các số thập phân sau:

   −18,5; 12,54; −0,08; 245,33.

   Lời giải:

   Cách tìm số đối của một số thập phân: ta thêm dấu trừ vào trước số thập phân đó.

   Số đối của −18,5 là −(−18,5) = 18,5.

   Số đối của 12,54 là −12,54.

   Số đối của −0,08 là −(−0,08) = 0,08.

   Số đối của 245,33 là −245,33.

   Bài 4 trang 48 sách bài tập Toán lớp 6 Tập 2: Hãy sắp xếp các số thập phân sau theo thứ tự tăng dần:

   12,79; −25,9; 0,12; −16,23; −0,41; 5,17.

   Lời giải:

   Để sắp xếp các số thập phân sau theo thứ tự tăng dần, ta làm như sau:

   Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.

   Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:

   – Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.

   – Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.

   Đối với bài toán này, ta thực hiện theo thứ tự các bước như trên:

   * Phân loại:

   – Nhóm các số thập phân dương: 12,79; 0,12; 5,17.

   – Nhóm các số thập phân âm: −25,9; −16,23; −0,41.

   * So sánh các số thập phân trong theo nhóm:

   – Nhóm các số thập phân dương: ta so sánh phần nguyên của các số trên, vì 0 < 5 < 12 nên 0,12 < 5,17 < 12,79.

   – Nhóm các số thập phân âm:

   + Số đối của các số −25,9; −16,23; −0,41 lần lượt là 25,9; 16,23; 0,41.

   + Ta so sánh phần nguyên của các số trên, vì 0 < 16 < 25 nên 0,41 < 16,23 < 25,9. Suy ra −0,41 > −16,23 > −25,9.

   Do đó −25,9 < −16,23 < −0,41 < 0,12 < 5,17 < 12,79.

   Vậy các số được sắp xếp thứ tự tăng dần là: −25,9; −16,23; −0,41; 0,12; 5,17; 12,79.

   Bài 5 trang 48 sách bài tập Toán lớp 6 Tập 2: Viết các số thập phân sau dưới dạng số thập phân tối giản:

   −0,45; 0,125; −4,25; −8,24.

   Lời giải:

   Để viết các số thập phân dưới dạng phân số tối giản thì ta đưa số thập phân về dạng phân số thập phân, sau đó rút gọn nếu có thể.

   Đổi lần lượt các số thập phân trên thành phân số, ta được:

   .

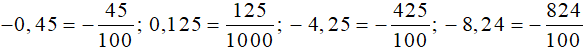   Rút gọn các phân số trên, ta được:

   .

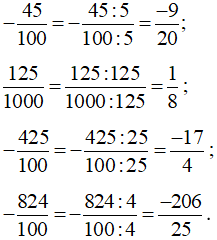   Vậy các số thập phân được viết dưới dạng phân số tối giản như sau: