Cho tam giác ABC, đường cao AH = 9 cm, cạnh BC = 12 cm. Diện tích tam giác là:

Câu hỏi:

Cho tam giác ABC, đường cao AH = 9 cm, cạnh BC = 12 cm. Diện tích tam giác là:

A. $108 c{m}^2$

B. $72 c{m}^2$

C. $54 c{m}^2$

Đáp án chính xác

D. $216 c{m}^2$

Trả lời:

Từ công thức tính diện tích tam giác ta cóS_ABC =$\frac{1}{2}$AH. BC = $\frac{1}{2}$.9.12 = 54 cm².Đáp án cần chọn là: C

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Giáo án Luyện tập Diện tích tam giác (2023) – Toán 8

   Mời các quý thầy cô cùng tham khảo và tải về chi tiết tài liệu dưới đây:

   Giáo án Luyện tập Toán 8 Bài 3: Diện tích tam giác

   A. Mục tiêu

   1. Kiến thức:

   – HS phát biểu được các công thức tính diện tích tam giác, các tính chất của diện tích.

   2. Kỹ năng:

   – HS biết cách vận dụng công thức và tính chất của diện tích để giải bài toán.

   – Biết cách vẽ HCN và tam giác có diện tích bằng diện tích cho trước.

   3. Thái độ:

   – Tích cực, tự giác, hợp tác.

   4. Phát triển năng lực:

   – Tính diện tích các hình cho trước.

   B. Chuẩn bị

   1. Giáo viên:

   – Bảng phụ hình 133 bài 19, hình 135 bài 22 (tr122-SGK), thước thẳng, phấn màu.

   2. Học sinh:

   – Compa, thước, bảng nhóm.

   C. Phương pháp

   – Vấn đáp, nêu và giải quyết vấn đề, thuyết trình, …

   D. Tiến trình dạy học

   1. Tổ chức lớp: Kiểm diện.

   2. Kiểm tra bài cũ: Phát biểu định lý về diện tích của tam giác và chứng minh định lý đó.

   3. Bài mới

   Hoạt động của giáo viên

   Hoạt động của học sinh

   Ghi bảng

   Hoạt động 1: Khởi động (7’)
   – Treo bảng phụ đưa ra đề kiểm tra, hình vẽ 133 (sgk) – Gọi HS lên bảng – Kiểm tra vở bài tập vài HS – Cho HS nhận xét câu trả lời và bài làm ở bảng – Đánh giá cho điểm	– HS đọc yêu cầu đề kiểm tra – Một HS lên bảng trả lời và làm bài, cả lớp làm vào vở bài tập: – Tham gia nhận xét câu trả lời và bài làm trên bảng. Tự sửa sai…	1.  Tính SABC biết BC = 3cm, đường cao AH = 0,2dm? 2.  a) Xem hình 133. Hãy chỉ ra các tam giác có cùng diện tích (lấy ô vuông làm đơn vị diện tích).   b) Hai tam giác có diện tích bằng nhau thì có bằng nhau không?
   Hoạt động 2: Luyện tập (32’)
   Bài 20 trang 122 SGK – Nêu bài 20, cho HS đọc đề bài Hỏi: Gthiết cho gì? Kluận gì? – Hãy phát hoạ và nghĩ xem vẽ như thế nào? – Gợi ý: – Dựa vào công thức tính diện tích các hình và điều kiện bài toán. – MN là đường trung bình của ∆ABC	– HS đọc đề bài 20 sgk – HS nêu GT – KL bài toán – Phát hoạ hình vẽ, suy nghĩ, trả lời – Thực hành giải theo nhóm:	Bài 20 trang 122 SGK
   Bài 20 trang 122 SGK
   – Nêu bài tập 13 sgk, vẽ hình 125 lên bảng. Hỏi: Dùng tính chất 1 và 2 về diện tích đa giác em có thể ghép hình chữ nhật EFBC và EGHD với những ∆ nào có cùng diện tích và có thể tạo ra những hình để so sánh diện tích? (Đường chéo AC tạo ra những ∆ nào có cùng diện tích?)	– Đọc đề bài, vẽ hình vào vở, ghi Gt – Kl. Quan sát hình vẽ, suy nghĩ cách giải ∆ABC = ∆CDA (c,c,c) ⇒ SABC = SADC. Tương tự ta cũng có: SAFE = SAHE ; SEKC  = SEGC Suy ra: SABC – SAFE – SEKC = SADC – SAHE – SEGC  Hay SEFBK = SEGDH	Hình chữ nhật ABCD
   Hoạt động 3: Vận dụng,mở rộng (20’)
   – Cho HS nhắc lại 3 tính chất cơ bản về diện tích đa giác	– HS nhắc lại tính chất cơ bản của đa giác
   – Học ôn các công thức tính diện tích đã học  – Chuẩn bị giấy làm bài kiểm tra 15’

   

2. Giải SGK Toán 8 Bài 3: Diện tích tam giác

   Giải bài tập Toán lớp 8 Bài 3: Diện tích tam giác

   Trả lời câu hỏi giữa bài

   Câu hỏi trang 121 Toán 8 Tập 1:Hãy cắt một tam giác thành ba mảnh để ghép lại thành một hình chữ nhật.

   Lời giải

   Ta thực hiện theo cách sau:

   

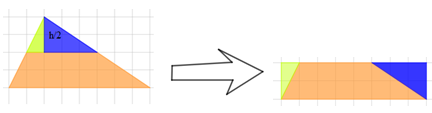
   Bài tập (trang 121, 122, 123)

   Bài 16 trang 121 Toán 8 Tập 1:Giải thích vì sao diện tích của tam giác được tô đậm trong hình 128, 129, 130 bằng nửa diện tích hình chữ nhật tương ứng.

   

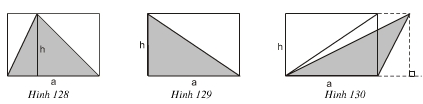
   Lời giải:

   Trong mỗi hình trên ta đều có:

   Diện tích hình chữ nhật là: a.h

   Diện tích tam giác trong cả ba hình là: $\frac{1}{2}.a.h$

   ⇒ Diện tích của tam giác bằng nửa diện tích hình chữ nhật tương ứng.

   Bài 17 trang 121 Toán 8 Tập 1:Cho tam giác AOB vuông tại O với đường cao OM (h.131). Hãy giải thích vì sao ta có đẳng thức AB.OM = OA.OB

   

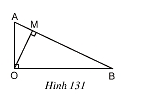
   Lời giải:

   Ta có cách tính diện tích ΔAOB với đường cao OM và cạnh đáy AB:

   $S=\frac{1}{2}OM.AB$

   Ta lại có cách tính diện tích ΔAOB vuông với hai cạnh góc vuông OA, OB là:

   $\begin{array}{l}S=\frac{1}{2}.OA.OB\\ \Rightarrow \frac{1}{2}OM.AB=\frac{1}{2}OA.OB\\ \Rightarrow OM.AB=OA.OB\end{array}$

   Bài 18 trang 121 Toán 8 Tập 1:Cho tam giác ABC và đường trung tuyến AM (h.132). Chứng minh: S_AMB = S_AMC

   

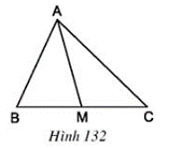
   Lời giải:

   Kẻ đường cao AH.

   

   Ta có:

   Diện tích tam giác AMB là: $S_{\Delta AMB}=\frac{1}{2}.MB.AH$

   Diện tích tam giác AMC là: $S_{\Delta AMC}=\frac{1}{2}.MC.AH$

   Mà BM = CM (vì AM là trung tuyến)

   ⇒ S_AMB = S_AMC (đpcm).

   Bài 19 trang 122 Toán 8 Tập 1:a) Xem hình 133. Hãy chỉ ra các tam giác có cùng diện tích (lấy ô vuông làm đơn vị diện tích)

   b) Hai tam giác có diện tích bằng nhau thì có bằng nhau hay không?

   

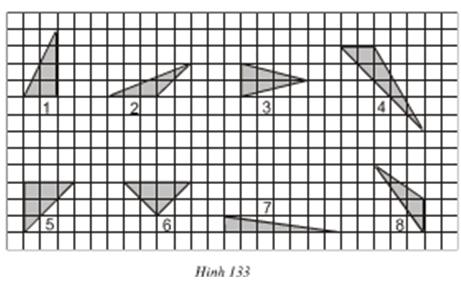
   Lời giải:

   a) Diện tích tam giác số 1:

   $\frac{1}{2}\mathrm{.2.4}=4$ (ô vuông)

   Diện tích tam giác số 2:

   $\frac{1}{2}\mathrm{.2.3}=3$ (ô vuông)

   Diện tích tam giác số 3:

   $\frac{1}{2}\mathrm{.2.4}=4$ (ô vuông)

   Diện tích tam giác số 4:

   $\frac{1}{2}\mathrm{.2.5}=5$ (ô vuông)

   Diện tích tam giác số 5:

   $\frac{1}{2}\mathrm{.3.3}=\frac{9}{2}$ (ô vuông)

   Diện tích tam giác số 6:

   $\frac{1}{2}\mathrm{.2.4}=4$ (ô vuông)

   Diện tích tam giác số 7:

   $\frac{1}{2}\mathrm{.1.7}=\frac{7}{2}$ (ô vuông)

   Diện tích tam giác số 8:

   $\frac{1}{2}\mathrm{.2.3}=3$ (ô vuông)

   Vậy:

   Các tam giác số 1, 3, 6 có cùng diện tích là 4 ô vuông.

   Các tam giác số 2, 8 có cùng diện tích là 3 ô vuông.

   b) Hai tam giác có diện tích bằng nhau thì không nhất thiết bằng nhau.

   Vì diện tích của tam giác là nửa tích của độ dài đáy với chiều cao tương ứng của đáy, nên chỉ cần tích của đáy với chiều cao bằng nhau thì hai tam giác đó có diện tích bằng nhau, hai cạnh còn lại có thể khác nhau.

   – Ví dụ như các tam giác 1, 3, 6 có cùng diện tích nhưng không bằng nhau.

   Bài 20 trang 122 Toán 8 Tập 1:Vẽ hình chữ nhật có một cạnh bằng cạnh của một tam giác cho trước và có diện tích bằng diện tích của tam giác đó. Từ đó suy ra một cách chứng minh khác về công thức tính diện tích tam giác.

   Lời giải:

   

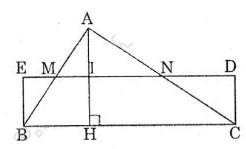
   Cho ΔABC với đường cao AH.

   Gọi M, N, I là trung điểm của AB, AC, AH.

   Lấy E đối xứng với I qua M, D đối xứng với I qua N.

   ⇒ Hình chữ nhật BEDC là hình cần dựng.

   Thật vậy:

   Xét ΔEBM và ΔIAM, có:

   ME = MI (E đối xứng với I qua M)

   $\widehat{EMB}=\widehat{AMI}$ (hai góc đối đỉnh)

   AM = MB (M là trung điểm của AB)

   Suy ra ΔEBM = ΔIAM

   Chứng minh tương tự ΔDCN = ΔIAN

   ⇒ S_EBM = S_AMI và S_CND = S_AIN

   ⇒ S_ABC = S_AMI + S_AIN + S_BMNC 

   = S_EBM + S_BMNC + S_CND = S_BCDE.

   Suy ra S_ABC = S_BCDE = BE.BC

   = $\frac{1}{2}$AH.BC. (Vì BE = IA = $\frac{AH}{2}$).

   Ta đã tìm lại công thức tính diện tích tam giác bằng một phương pháp khác

   Bài 21 trang 122 Toán 8 Tập 1:Tính x sao cho diện tích hình chữ nhật. ABCD gấp ba lần diện tích tam giác ADE (h.134).

   

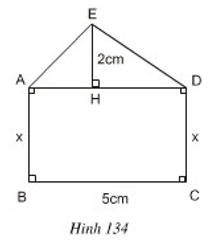
   Lời giải:

   Vì ABCD là hình chữ nhật nên AD = BC = 5cm.

   Diện tích ΔADE: $S_{\Delta ADE}=\frac{1}{2}\mathrm{.2.5}=5\left(c{m}^2\right)$

   Diện tích hình chữ nhật ABCD: S_ABCD = 5x

   Theo đề bài ta có

   S_ABCD = 3S_ADE ⇔ 5x = 3.5 ⇔ x = 3.

   Vậy x = 3cm

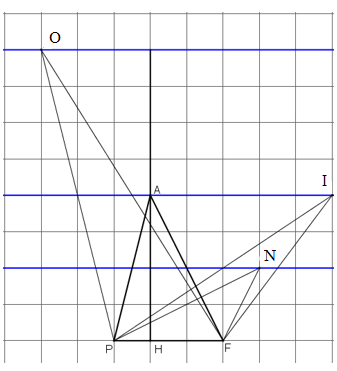
   Bài 22 trang 122 Toán 8 Tập 1:Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135). Hãy chỉ ra:

   

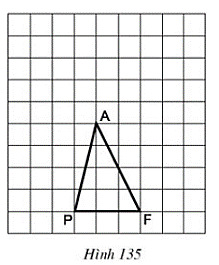
   a) Một điểm I sao cho S_PIF = S_PAF

   b) Một điểm O sao cho S_POF = 2.S_PAF

   c) Một điểm N sao cho $S_{PNF}=\frac{1}{2}{S}_{\text{PAF}}$

   Phân tích đề:

   Cả 3 phần a, b, c đều liên quan đến so sánh diện tích một tam giác với S_PAF. Mà diện tích một tam giác = nửa tích của chiều cao nhân với một cạnh tương ứng, mà trong bài này đều có chung cạnh tương ứng là PF nên việc giải bài toán chỉ cần xác định các điểm sao cho khoảng cách từ điểm đó đến PF thỏa mãn yêu cầu đề bài là được.

   Lời giải:

   Gọi AH là chiều cao của tam giác APF.

   Ta có: S_APF = $\frac{1}{2}FA.AH$.

   a) Hai tam giác PIF và tam giác PAF có cùng đáy PF

   Nên để S_PIF = S_PAF thì chiều cao IK = AH ( với IK là chiều cao của tam giác PIF ứng với cạnh PF).

   Do đó I nằm trên đường thẳng song song với PF và cách PF một khoảng bằng AH.

   b) Tam giác POF và tam giác PAF là hai tam giác có chung cạnh PF

   Nên để S_POF = 2.S_PAF thì chiều cao OM = 2AH (với OM là chiều cao của tam giác POF ứng với cạnh PF)

   Do đó O nằm trên đường thẳng song song với PF và cách PF một khoảng bằng 2.AH

   c) Tam giác PNF và tam giác PAF có chung cạnh PF

   Nên để $S_{PNF}=\frac{1}{2}{S}_{\text{PAF}}$ thì chiều cao NQ = $\frac{1}{2}AH$ (với NQ là chiều cao của tam giác PNF ứng với cạnh PF)

   Do đó N nằm trên đường thẳng song song với PF và cách PF một khoảng bằng $\frac{AH}{2}$.

   

   Bài 23 trang 123 Toán 8 Tập 1:Cho tam giác ABC. Hãy chỉ ra một số vị trí của điểm M nằm trong tam giác đó sao cho: S_AMB + S_BMC = S_MAC

   Lời giải:

   

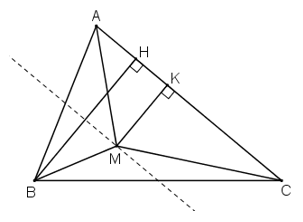
   Giả sử tìm được điểm M nằm trong tam giác ABC thỏa mãn điều kiện đã cho

   Kẻ đường cao BH, MK.

   Ta có: S_AMB + S_BMC + S_MAC = S_ABC (1)

   Mà S_AMB + S_BMC = S_MAC (2)

   Thay (2) vào (1), ta được:

   $\begin{array}{l}\Rightarrow S_{AMC}+S_{AMC}=S_{ABC}\\ \Rightarrow 2S_{AMC}=S_{ABC}\\ \Rightarrow S_{AMC}=\frac{1}{2}{S}_{ABC}\end{array}$

   Vì tam giác AMC và tam giác ABC có chung cạnh AC nên $MK=\frac{1}{2}BH$.

   Do đó, M nằm trong ΔABC, nằm trên đường thẳng d bờ AC chứa B sao cho khoảng cách từ M đến AC một nửa đường cao BH.

   Suy ra điểm M nằm trong ΔABC nằm trên đường trung bình của ΔABC.

   Bài 24 trang 123 Toán 8 Tập 1:Tính diện tích của một tam giác cân có cạnh đáy bằng a và cạnh bên bằng b.

   Lời giải:

   

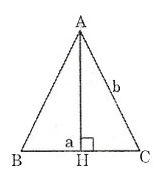
   Xét tam giác ABC cân tại A, kẻ đường cao AH.

   $\Rightarrow$H là trung điểm của BC

   $\Rightarrow BH=HC=\frac{BC}{2}=\frac{a}{2}$

   Gọi h là chiều cao của tam giác cân ABC.

   Xét tam giác AHC vuông tại C

   $A{C}^2=A{H}^2+H{C}^2$ (định lý Py – ta – go)

   $\begin{array}{l}\iff b^2=A{H}^2+{\left(\frac{a}{2}\right)}^2\\ \iff b^2-{\left(\frac{a}{2}\right)}^2=A{H}^2\\ \iff b^2-\frac{a^2}{4}=A{H}^2\\ \iff \frac{4b^2-a^2}{4}=A{H}^2\\ \iff \sqrt{\frac{4b^2-a^2}{4}}=AH\\ \iff AH=\frac{\sqrt{4b^2-a^2}}{2}.\end{array}$

   Diện tích tam giác cân ABC là:

   $\frac{1}{2}AH.BC=\frac{1}{2}.\frac{\sqrt{4b^2-a^2}}{2}.a$

   $=\frac{a\sqrt{4b^2-a^2}}{4}$ (đvdt).

   Vậy diện tích tam giác cân ABC là: $\frac{a\sqrt{4b^2-a^2}}{4}$.

   Bài 25 trang 123 Toán 8 Tập 1:Tính diện tích của một tam giác đều có cạnh bằng a.

   Lời giải:

   

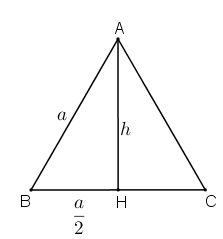
   Xét tam giác đều ABC cạnh a. Dựng đường cao AH.

   Trong tam giác đều, đường cao đồng thời là đường trung tuyến nên H là trung điểm BC.

   $BH=CH= \frac{a}{2}$

   Xét tam giác vuông AHB ta được:

   $A{H}^2+H{B}^2=A{B}^2$ (định lý Py – ta – go)

   $\begin{array}{l}\iff A{H}^2=A{B}^2-H{B}^2\\ \iff A{H}^2=a^2-{\left(\frac{a}{2}\right)}^2\\ \iff A{H}^2=a^2-\frac{a^2}{4}=\frac{3a^2}{4}\\ \iff AH=\frac{\sqrt{3}a}{2}\end{array}$

   Diện tích tam giác ABC là:

   $S_{ABC}=\frac{1}{2}BC.AH$

   $=\frac{1}{2}.a.\frac{a\sqrt{3}}{2}=\frac{a^2\sqrt{3}}{4}$(đvdt).

3. 50 Bài tập Diện tích hình tam giác (có đáp án)- Toán 5

   Tailieumoi.vn xin giới thiệu Bài tập Toán 5 Chương 3 Bài 86: Diện tích hình tam giác. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 5. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 86: Diện tích hình tam giác. Mời các bạn đón xem:

   Bài tập Toán 5 Bài 86: Diện tích hình tam giác

   A. Bài tập Diện tích hình tam giác

   I. Bài tập trắc nghiệm

   Câu 1: Tính diện tích hình tam giác có độ dài đáy là 5m và chiều cao là 27dm.

   A. 67,5dm²

   B. 67,5dm²

   C. 675dm²

   D. 675dm²

   Đổi 5m = 50dm

   Diện tích tam giác đó là:

    = 675 (dm²)

   Đáp số: 675 dm²

   Câu 2: Tính diện tích tam giác vuông ABC có kích thước như hình vẽ bên dưới:

   

   A. 140cm²

   B. 280dm²

   C. 14dm²

   D. 28cm²

   Đổi 2dm = 20cm

   Diện tích tam giác vuông ABC là:

    = 140 (cm²)

   Đáp số: 140 cm²

   Câu 3: Độ dài cạnh đáy của hình tam giác có chiều cao 24cm và diện tích là 420cm² là:

   A. 17,5cm

   B. 23,5cm

   C. 35cm

   D. 396cm

   Độ dài cạnh đáy của hình tam giác đó là:

   420 × 2 : 24 = 35 (cm)

   Đáp số: 35cm

   Câu 4: Điền số thích hợp vào ô trống:

   Một hình tam giác có diện tích là 8m² và độ dài cạnh đáy là 32dm.

   Vậy chiều cao tương ứng với cạnh đáy đó là  dm.

   Đổi 8 m² = 800 dm²

   Chiều cao của tam giác đó là:

   800 × 2 : 32 = 50 (dm)

   Đáp số: 50dm.

   Vậy đáp án đúng điền vào ô trống là 50.

   Câu 5: Cho hình vẽ như bên dưới:

   

   Tính diện tích hình tam giác HDC. Biết hình chữ nhật ABCD có AB = 37cm, BC = 24cm.

   A. 444cm²

   B. 888cm²

   C. 1234cm²

   D. 1776cm²

   

   Kẻ HK vuông góc với CD, khi đó HK là chiều cao tương ứng với cạnh đáy CD.

   Ta có chiều cao HK bằng chiều rộng của hình chữ nhật ABCD hay HK = BC = 24cm

   Vì ABCD là hình chữ nhật nên CD = AB = 37cm.

   Diện tích tam giác HDC là:

   37 × 24 : 2 = 444 (cm²)

   Đáp số: 444cm²

   Câu 6: Trong một tam giác có:

   A. 3 cạnh

   B. 3 góc

   C. 3 đỉnh

   D. Cả A, B, C đều đúng

   Một tam giác có 3 cạnh, 3 góc và 3 đỉnh.

   Vậy cả A, B, C đều đúng.

   Câu 7: Nối câu mô tả hình dạng với hình tam giác tương ứng:

   

    

   Quan sát các tam giác theo thứ tự từ trên xuống dưới ta có:

   – Hình tam giác thứ nhất có một góc vuông và hai góc nhọn

   – Hình tam giác thứ hai có một góc tù và hai góc nhọn.

   – Hình tam giác thứ ba có ba góc nhọn.

   Câu 8: Cho hình vẽ như bên dưới:

   

   Trong tam giác MNP, MK là chiều cao tương ứng với:

   A. Cạnh MN

   B. Cạnh NP

   C. Cạnh MP

   D. Cạnh KN

   Hình tam giác MNP có MK vuông góc với NP, do đó MK là chiều cao tương ứng với cạnh đáy NP.

   Câu 9: Điền số thích hợp vào ô trống:

   Diện tích hình tam giác có độ dài đáy là 25cm và chiều cao là 16cm là  cm².

   Diện tích tam giác đó là:

    = 200 (cm²)

   Đáp án: 200cm².

   Vậy đáp án đúng điền vào ô trống là 200.

   Câu 10: Điền số thích hợp vào ô trống:

   Một miếng đất hình chữ nhật có chu vi là 86m, chiều dài 28m. Ở giữa miếng đất, người ta làm một bồn hoa hình tam giác có chiều cao 9,6m và bằng  cạnh đáy.

   Vậy diện tích miếng đất còn lại là  m².

   Nửa chu vi miếng đất hình chữ nhật đó là:

   86 : 2 = 43 (m)

   Chiều rộng miếng đất đó là:

   43 – 28 = 15 (m)

   Diện tích miếng đất hình chữ nhật đó là:

   28 × 15 = 420 (m²)

   Độ dài cạnh đáy của bồn hoa là:

   9,6 : 3 × 5 = 16 (m)

   Diện tích bồn hoa hình tam giác đó là:

   16 × 9,6 : 2 = 76,8 (m²)

   Diện tích miếng đất còn lại là:

   420 − 76,8 = 343,2 (m²)

   Đáp số: 343,2m².

   Vậy đáp án đúng điền vào ô trống là 343,2.

   II. Bài tập tự luận

   Câu 1: Tính diện tích hình tam giác AHK. Biết hình vuông ABCD có cạnh 16cm và BK = KC, DH = HC.

   

   Đáp án
   

   Ta có ABCD là hình vuông cạnh 16cm nên AB = BC = CD = AD = 16cm.

   Lại có theo đề bài BK = KC, DH = HC nên BK = KC = DH = HC = 16 : 2 = 8cm.

   Diện tích hình vuông ABCD là:

   16 × 16 = 256 (cm²)

   Diện tích hình tam giác ABK là:

   16 × 8 : 2 = 64 (cm²)

   Diện tích hình tam giác KCH là:

   8 × 8 : 2 = 32 (cm²)

   Diện tích hình tam giác ADH là:

   16 × 8 : 2 = 64 (cm²)

   Diện tích hình tam giác AHK là:

   256 − (64 + 32 + 64) = 96 (cm²)

   Đáp số: 96cm².

   Câu 2: Một thửa ruộng hình tam giác vuông có tổng hai cạnh góc vuông là 72m và cạnh góc vuông này bằng 0,6 lần cạnh góc vuông kia. Trên thửa ruộng này người ta trồng lúa, trung bình cứ 100m² thu được 60kg thóc. Hỏi trên cả thửa ruộng, người ta thu hoạch được bao nhiêu tạ thóc?

   Đáp án
   

   Đổi 0,6 = 

   Ta có sơ đồ:

   

   Tổng số phần bằng nhau là :

   3 + 5 = 8 (phần)

   Giá trị một phần là:

   72 : 8 = 9 (m)

   Độ dài một cạnh góc vuông là:

   9 × 3 = 27 (m)

   Độ dài cạnh góc vuông còn lại là:

   72 – 27 = 45 (m)

   Diện tích thửa ruộng đó là:

   45 × 27 : 2 = 607,5 (m²)

   607,5m² gấp 100m² số lần là:

   607,5 : 100 = 6,075 (lần)

   Trên cả thửa ruộng, người ta thu hoạch được số thóc là:

   60 × 6,075 = 364,5 (kg)

   364,5kg = 3,645 tạ

   Đáp số: 3,645 tạ.

   Câu 3: Điền số thích hợp vào ô trống:

   Cho tam giác MNP có MP = 32cm, NP = 36cm. Biết chiều cao tương ứng với đáy NP là MH = 24cm.

   Vậy chiều cao tương ứng với đáy MP là NK =  cm.

   Đáp án
   

   Theo đề bài ta có hình vẽ:

   

   Diện tích tam giác MNP là:

   36 × 24 : 2 = 432 (cm²)

   Độ dài chiều cao NK là:

   432 × 2 : 32 = 27 (cm)

   Đáp số: 27cm.

   Vậy đáp án đúng điền vào ô trống là 27.

   III. Bài tập vận dụng

   Câu 1: Cho tam giác ABC có BC = 67dm. Nếu kéo dài đoạn BC thêm một đoạn CD = 15dm thì diện tích tam giác tăng thêm 255dm². Tính diện tích tam giác ABC.

   Đáp án
   

   Theo bài ra ta có hình vẽ:

   

   Phần diện tích tăng thêm chính là diện tích của hình tam giác có đáy là 15dm và chiều cao cũng chính là chiều cao AH của tam giác ABC.

   Chiều cao của tam giác ABC là:

   255 × 2 : 15 = 34 (dm)

   Diện tích tam giác ABC là

   67 × 34 : 2 = 1139 (dm²)

   Đáp số: 1139dm².

   Câu 2: Cho hình vẽ như bên dưới:

   

   Tính diện tích hình tam giác HDC. Biết hình chữ nhật ABCD có AB = 37cm, BC = 24cm.

   Đáp án
   

   

   Kẻ HK vuông góc với CD, khi đó HK là chiều cao tương ứng với cạnh đáy CD.

   Ta có chiều cao HK bằng chiều rộng của hình chữ nhật ABCD hay HK = BC = 24cm

   Vì ABCD là hình chữ nhật nên CD = AB = 37cm.

   Diện tích tam giác HDC là:

   37 × 24 : 2 = 444 (cm²)

   Đáp số: 444cm²

   Câu 3: Điền số thích hợp vào ô trống:

   Một miếng đất hình chữ nhật có chu vi là 86m, chiều dài 28m. Ở giữa miếng đất, người ta làm một bồn hoa hình tam giác có chiều cao 9,6m và bằng  cạnh đáy.

   Vậy diện tích miếng đất còn lại là  m².

   Đáp án
   

   Nửa chu vi miếng đất hình chữ nhật đó là:

   86 : 2 = 43 (m)

   Chiều rộng miếng đất đó là:

   43 – 28 = 15 (m)

   Diện tích miếng đất hình chữ nhật đó là:

   28 × 15 = 420 (m²)

   Độ dài cạnh đáy của bồn hoa là:

   9,6 : 3 × 5 = 16 (m)

   Diện tích bồn hoa hình tam giác đó là:

   16 × 9,6 : 2 = 76,8 (m²)

   Diện tích miếng đất còn lại là:

   420 − 76,8 = 343,2 (m²)

   Đáp số: 343,2m2.

   Vậy đáp án đúng điền vào ô trống là 343,2.

   B. Lý thuyết Diện tích hình tam giác

   1. Diện tích hình tam giác

   Quy tắc: Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2

   

   $S=\frac{a\times h}{2} hoặc S = a\times h:2$

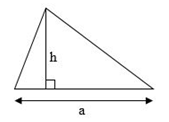
   (S là diện tích, a là độ dài đáy, h là chiều cao)

   Chú ý: Muốn tính diện tích tam giác vuông ta lấy độ dài hai cạnh góc vuông nhân với nhau (cùng một đơn vị đo) rồi chia cho 2.

   Ví dụ 1: Tính diện tích hình tam giác có độ dài đáy là 13cm và chiều cao là 8cm.

   Phương pháp giải: Độ dài đáy và chiều cao đã có cùng đơn vị đo nên để tính diện tích ta lấy độ dài đáy nhân với chiều cao rồi chia cho 2.

   Cách giải:

   Diện tích hình tam giác đó là:

   13 x 8 : 2 = 52 (cm²)

   Đáp số: 52cm²

   Ví dụ 2: Tính diện tích hình tam giác có độ dài đáy là 2m và chiều cao là 15dm.

   Phương pháp giải: Độ dài đáy và chiều cao chưa cùng đơn vị đo nên ta đổi về cùng đơn vị đo, 2m = 20dm, sau đó tính diện tích ta lấy độ dài đáy nhân với chiều cao rồi chia cho 2

   Bài giải

   Đổi: 2m = 20dm

   Diện tích hình tam giác đó là:

   20 x 15 : 2 = 150 dm²

   Đáp số: 150 dm²

4. Hình tam giác vuông có 1 cạnh góc vuông giảm đi 3 lần và cạnh góc vuông còn lại tăng lên 3 lần, khi đó diện tích hình tam giác vuông mới
   
   

   Câu hỏi:
   

   Hình tam giác vuông có 1 cạnh góc vuông giảm đi 3 lần và cạnh góc vuông còn lại tăng lên 3 lần, khi đó diện tích hình tam giác vuông mới

   A. Không thay đổi

   Đáp án chính xác

   B. Tăng 3 lần

   C. Giảm 6 lần

   D. Giảm 3 lần

   Trả lời:

   Theo công thức tính diện tích tam giác vuông có 2 cạnh góc vuông có độ dài là a,b là  $S=\frac{1}{2}a.b$Tam giác vuông mới có độ dài hai cạnh là a’ và b’Theo đề bài  $a‘=\frac{a}{3},b‘=3b$Khi đó, diện tích  $S‘=\frac{1}{2}a‘.b‘=\frac{1}{2}\frac{a}{3}.3b=\frac{1}{2}ab=S$Do đó diện tích hình tam giác mới không thay đổi so với tam giác ban đầuĐáp án cần chọn là: A

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

5. Cho tam giác ABC, biết diện tích tam giác là 16 cm2 và cạnh BC = 8 cm. Đường cao tương ứng với cạnh BC là:
   
   

   Câu hỏi:
   

   Cho tam giác ABC, biết diện tích tam giác là $16 c{m}^2$ và cạnh BC = 8 cm. Đường cao tương ứng với cạnh BC là:

   A. 5 cm

   B. 8 cm

   C. 6 cm

   D. 4 cm

   Đáp án chính xác

   Trả lời:

   Gọi AH là đường cao ứng với cạnh BC. Theo công thức tính diện tích tam giác ta cóS = $\frac{1}{2}$AH. BC ó$\frac{1}{2}$AH.8 = 16ó AH = 4 cm.Đáp án cần chọn là: D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====