Lý thuyết Giới hạn của hàm số (Kết nối tri thức 2023) hay, chi tiết | Toán lớp 11

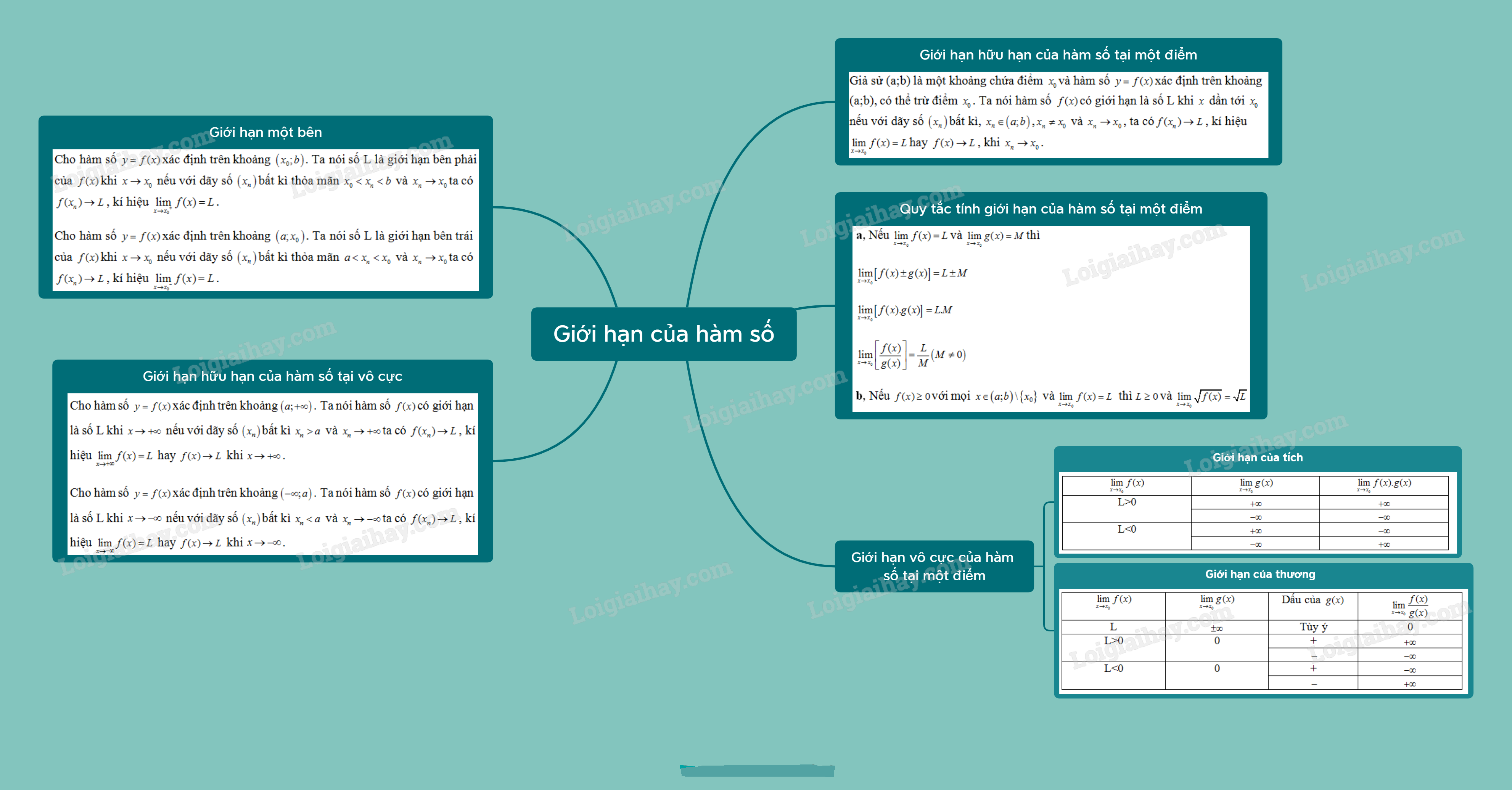
Lý thuyết Toán lớp 11 Bài 16: Giới hạn của hàm số
A. Lý thuyết Giới hạn của hàm số
1. Giới hạn hữu hạn của hàm số tại một điểm
Giả sử (a;b) là một khoảng chứa điểm $x_0$và hàm số $y=f(x)$xác định trên khoảng (a;b), có thể trừ điểm $x_0$. Ta nói hàm số $f(x)$có giới hạn là số L khi $x$ dần tới $x_0$ nếu với dãy số $\left(x_n\right)$bất kì, $x_n\in \left(a;b\right)$,$x_n\ne x_0$ và $x_n\to x_0$, ta có$f(x_n)\to L$, kí hiệu $\underset{x\to x_0}{lim}f(x)=L$hay $f(x)\to L$, khi $x_n\to x_0$.
*Quy tắc tính giới hạn của hàm số tại một điểm
a, Nếu $\underset{x\to x_0}{lim}f(x)=L$và $\underset{x\to x_0}{lim}g(x)=M$thì
$\underset{x\to x_0}{lim}\left[f(x)\pm g(x)\right]=L\pm M$
$\underset{x\to x_0}{lim}\left[f(x).g(x)\right]=L.M$
$\underset{x\to x_0}{lim}\left[\frac{f(x)}{g(x)}\right]=\frac{L}{M}\left(M\ne 0\right)$
b, Nếu $f(x)\ge 0$với mọi $x\in \left(a;b\right)\mathrm{\setminus }\left\{x_0\right\}$ và $\underset{x\to x_0}{lim}f(x)=L$ thì $L\ge 0$và $\underset{x\to x_0}{lim}\sqrt{f(x)}=\sqrt{L}$.
2. Giới hạn một bên
Cho hàm số $y=f(x)$xác định trên khoảng $\left(x_0;b\right)$. Ta nói số L là giới hạn bên phải của $f(x)$khi $x\to x_0$ nếu với dãy số $\left(x_n\right)$bất kì thỏa mãn $x_0<x_n<b$ và $x_n\to x_0$ta có $f(x_n)\to L$, kí hiệu $\underset{x\to {x_0}^{+}}{lim}f(x)=L$.
Cho hàm số $y=f(x)$xác định trên khoảng $\left(a;x_0\right)$. Ta nói số L là giới hạn bên trái của khi $x\to x_0$ nếu với dãy số $\left(x_n\right)$bất kì thỏa mãn $a<x_n<x_0$ và $x_n\to x_0$ta có $f(x_n)\to L$, kí hiệu $\underset{x\to {x_0}^{-}}{lim}f(x)=L$.
3. Giới hạn hữu hạn của hàm số tại vô cực
Cho hàm số $y=f(x)$xác định trên khoảng $\left(a;+\mathrm{\infty }\right)$. Ta nói hàm số $f(x)$có giới hạn là số L khi $x\to +\mathrm{\infty }$ nếu với dãy số $\left(x_n\right)$bất kì $x_n>a$ và $x_n\to +\mathrm{\infty }$ta có $f(x_n)\to L$, kí hiệu $\underset{x\to +\mathrm{\infty }}{lim}f(x)=L$ hay $f(x)\to L$ khi $x\to +\mathrm{\infty }$.
Cho hàm số $y=f(x)$xác định trên khoảng $\left(-\mathrm{\infty };b\right)$. Ta nói hàm số $f(x)$có giới hạn là số L khi $x\to -\mathrm{\infty }$ nếu với dãy số $\left(x_n\right)$bất kì $x_n<b$ và $x_n\to -\mathrm{\infty }$ta có $f(x_n)\to L$, kí hiệu $\underset{x\to -\mathrm{\infty }}{lim}f(x)=L$ hay $f(x)\to L$ khi $x\to -\mathrm{\infty }$.
* Nhận xét:
Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.
Với c là hằng số, $\underset{x\to +\mathrm{\infty }}{lim}c=c$, $\underset{x\to -\mathrm{\infty }}{lim}c=c$.
Với k là một số nguyên dương, ta có: $\underset{x\to +\mathrm{\infty }}{lim}(\frac{1}{x^k})=0,\underset{x\to -\mathrm{\infty }}{lim}(\frac{1}{x^k})=0$.
4. Giới hạn vô cực của hàm số tại một điểm
a, Giới hạn vô cực
– Giả sử (a;b) là một khoảng chứa $x_0$và hàm số $y=f(x)$xác định trên khoảng $\left(a;b\right)\mathrm{\setminus }\left\{x_0\right\}$. Ta nói hàm số $f(x)$có giới hạn là $+\mathrm{\infty }$khi $x$ dần tới $x_0$ nếu với dãy số $\left(x_n\right)$bất kì, $\left(a;b\right)\mathrm{\setminus }\left\{x_0\right\}$ và $x_n\to x_0$, ta có$f(x_n)\to +\mathrm{\infty }$, kí hiệu $\underset{x\to x_0}{lim}f(x)=+\mathrm{\infty }$
Ta nói hàm số $f(x)$có giới hạn $-\mathrm{\infty }$khi $x\to x_0$, kí hiệu $\underset{x\to x_0}{lim}f(x)=-\mathrm{\infty }$, nếu $\underset{x\to x_0}{lim}\left[-f(x)\right]=+\mathrm{\infty }$.
– Cho hàm số $y=f(x)$xác định trên khoảng $\left(x_0;b\right)$. Ta nói hàm số $f(x)$có giới hạn $+\mathrm{\infty }$ khi $x\to x_0$ về bên phải nếu với dãy số $\left(x_n\right)$bất kì thỏa mãn $x_0<x_n<b$ và $x_n\to x_0$ta có $f(x_n)\to +\mathrm{\infty }$, kí hiệu $\underset{x\to {x_0}^{+}}{lim}f(x)=+\mathrm{\infty }$.
Cho hàm số $y=f(x)$xác định trên khoảng $\left(a;x_0\right)$. Ta nói hàm số $f(x)$có giới hạn $+\mathrm{\infty }$ khi $x\to x_0$ về bên trái nếu với dãy số $\left(x_n\right)$bất kì thỏa mãn $a<x_n<x_0$ và $x_n\to x_0$ta có $f(x_n)\to +\mathrm{\infty }$, kí hiệu $\underset{x\to {x_0}^{-}}{lim}f(x)=+\mathrm{\infty }$.
Các giới hạn một bên$\underset{x\to {x_0}^{+}}{lim}f(x)=-\mathrm{\infty }$, $\underset{x\to {x_0}^{-}}{lim}f(x)=-\mathrm{\infty }$ được định nghĩa tương tự.
b, Một số quy tắc tính giới hạn vô cực
*Giới hạn của tích$\underset{x\to x_0}{lim}f(x).g(x)$
 
*Giới hạn của thương $\frac{f(x)}{g(x)}$
 
 

 
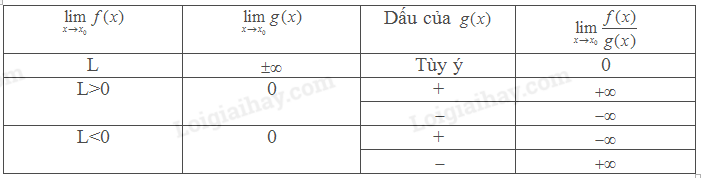
B. Bài tập Giới hạn của hàm số
Đang cập nhật …
Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 12: Đường thẳng và mặt phẳng song song
Lý thuyết Bài 13: Hai mặt phẳng song song
Lý thuyết Bài 14: Phép chiếu song song
Lý thuyết Bài 15: Giới hạn của dãy số
Lý thuyết Bài 16: Giới hạn của hàm số
Lý thuyết Bài 17: Hàm số liên tục
Xem thêm các bài tóm tắt lý thuyết chương Toán lớp 11 Kết nối tri thức hay, chi tiết khác
Lý thuyết Chương 1: Hàm số lượng giác và phương trình lượng giác
Lý thuyết Chương 2: Dãy số. Cấp số cộng và cấp số nhân
Lý thuyết Chương 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu ghép nhóm
Lý thuyết Chương 4: Quan hệ song song trong không gian
Lý thuyết Chương 5: Giới hạn. Hàm số liên tục

==== ~~~~~~ ====