Giải SBT Toán lớp 10 Bài 3: Các phép toán trên tập hợp
Giải SBT Toán 10 trang 16 Tập 1
Bài 1 trang 16 SBT Toán 10 Tập 1: Xác định A ∩ B, A ∪ B, A \ B, B \ A trong các trường hợp sau:
a) A = {a; b; c; d}, B = {a; c; e};
b) A = {x | x2 – 5x – 6 = 0}, B = {x | x2 = 1};
c) A = {x ∈ ℕ | x là số lẻ, x < 8}, B = {x ∈ ℕ | x là các ước của 12}.
Lời giải:
a) Ta có: A ∩ B = {x | x ∈ A và x ∈ B}
Các phần tử vừa thuộc A vừa thuộc B là: a; c.
Do đó A ∩ B = {a; c}.
Ta có: A ∪ B = {x | x ∈ A hoặc x ∈ B}
Các phần tử thuộc A hoặc thuộc B là: a; b; c; d; e.
Do đó A ∪ B = {a; b; c; d; e},
Ta có: A \ B = {x | x ∈ A và x ∉ B}
Các phần tử thuộc A nhưng không thuộc B là: b; d.
Do đó A \ B = {b; d}.
Ta có: B \ A = {x | x ∈ B và x ∉ A}
Phần tử thuộc B nhưng không thuộc A là: e.
Do đó, B \ A = {e}.
b) Giải phương trình x2 – 5x – 6 = 0.
Ta có: x2 – 5x – 6 = 0
⇔ x2 + x – 6x – 6 = 0
⇔ x(x + 1) – 6(x + 1) = 0
⇔ (x – 6)(x + 1) = 0
⇔ x = 6 hoặc x = – 1.
Do đó, A = {– 1; 6}.
Ta có: x2 = 1 ⇔ x = 1 hoặc x = – 1.
Do đó, B = {– 1; 1}.
Vậy A ∩ B = {x | x ∈ A và x ∈ B} = {– 1};
A ∪ B = {x | x ∈ A hoặc x ∈ B} = {– 1; 1; 6};
A \ B = {x | x ∈ A và x ∉ B} = {6};
B \ A = {x | x ∈ B và x ∉ A} = {1}.
c) Các số tự nhiên lẻ nhỏ hơn 8 là: 1; 3; 5; 7. Do đó, A = {1; 3; 5; 7}.
Các số tự nhiên là ước của 12 là: 1; 2; 3; 4; 6; 12. Do đó, B = {1; 2; 3; 4; 6; 12}.
Vậy A ∩ B = {x | x ∈ A và x ∈ B} = {1; 3};
A ∪ B = {x | x ∈ A hoặc x ∈ B} = {1; 2; 3; 4; 5; 6; 7; 12};
A \ B = {x | x ∈ A và x ∉ B} = {5; 7};
B \ A = {x | x ∈ B và x ∉ A} = {2; 4; 6; 12}.
Bài 2 trang 16 SBT Toán 10 Tập 1: Cho hai tập hợp A = {(x; y) | 3x – 2y = 11}, B = {(x ; y) | 2x + 3y = 3}. Hãy xác định tập hợp A ∩ B.
Lời giải:
Ta thấy (x; y) ∈ A ∩ B khi (x; y) là nghiệm của hệ phương trình:.
Nhân hai vế của (1) với 3, nhân hai vế của (2) với 2, ta được hệ phương trình
Cộng vế với vế hai phương trình của hệ này, ta được 13x = 39 hay x = 3.
Thay x = 3 vào (1) ta được 3 . 3 – 2y = 11, suy ra y = – 1.
Do đó, hệ phương trình (I) có một nghiệm là (3; – 1).
Vậy A ∩ B = {(3; – 1)}.
Bài 3 trang 16 SBT Toán 10 Tập 1: Cho các tập hợp A = {1; 3; 5; 7; 9}, B = {1; 2; 3; 4}, C = {3; 4; 5; 6}. Hãy xác định các tập hợp:
a) (A ∪ B) ∩ C;
b) A ∩ (B ∩ C);
c) A \ (B ∩ C);
d) (A \ B) ∪ (A \ C).
Lời giải:
a) Ta có: A ∪ B = {x | x ∈ A hoặc x ∈ B} = {1; 2; 3; 4; 5; 7; 9}.
Do đó, (A ∪ B) ∩ C = {x | x ∈ (A ∪ B) và x ∈ C} = {3; 4; 5}.
b) Ta có: B ∩ C = {x | x ∈ B và x ∈ C} = {3; 4}.
Do đó, A ∩ (B ∩ C) = {x | x ∈ A và x ∈ (B ∩ C)} = {3}.
c) Ta có: A \ (B ∩ C) = {x | x ∈ A và x ∉ (B ∩ C)} = {1; 5; 7; 9}.
d) Ta có: A \ B = {x | x ∈ A và x ∉ B} = {5; 7; 9}.
A \ C = {x | x ∈ A và x ∉ C} = {1; 7; 9}.
Do đó, (A \ B) ∪ (A \ C) = {x | x ∈ (A \ B) hoặc x ∈ (A \ C)} = {1; 5; 7; 9}.
Giải SBT Toán 10 trang 17 Tập 1
Bài 4 trang 17 SBT Toán 10 Tập 1: Kí hiệu A là tập hợp các học sinh nữ của trường, B là tập hợp các học sinh khối 10 của trường; C, D lần lượt là tập hợp các học sinh nữ, các học sinh nam khối 10 của trường (Hình 7). Hãy điền kí hiệu tập hợp thích hợp vào chỗ chấm.
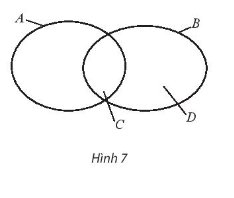
a) A ∩ B = …;
b) C ∪ D = …;
c) B \ A = …;
d) B ∩ C = …;
e) C \ A = …;
g) D \ A = …;
Lời giải:
a) Do A là tập hợp các học sinh nữ của trường và B là tập hợp các học sinh khối 10 của trường nên A ∩ B là tập hợp các học sinh nữ khối 10 của trường và chính là tập C.
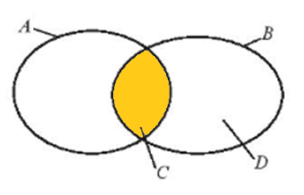
Do đó, A ∩ B = C.
b) Do C, D lần lượt là tập hợp các học sinh nữ, các học sinh nam khối 10 của trường nên C ∪ D là tập hợp các học sinh khối 10 của trường và chính là tập hợp B.
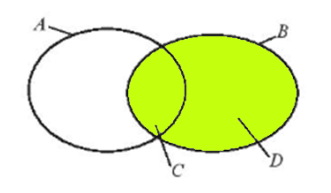
Do đó, C ∪ D = B.
c) B \ A là tập hợp các phần tử thuộc B nhưng không thuộc A, mà B là tập hợp các học sinh khối 10 của trường và A là tập hợp các học sinh nữ của trường, do đó B \ A là tập hợp các học sinh nam khối 10 của trường và chính là tập hợp D.
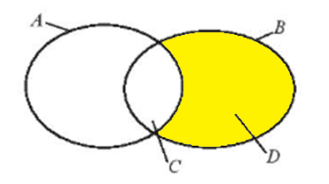
Vậy B \ A = D.
d) B ∩ C là tập hợp các phần tử vừa thuộc B vừa thuộc C, mà B là tập hợp các học sinh khối 10 của trường và C là tập hợp các học sinh nữ khối 10 của trường nên B ∩ C = C.
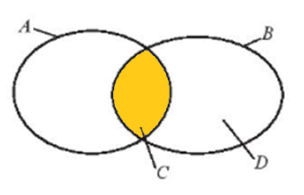
e) C \ A là tập hợp các phần tử thuộc C nhưng không thuộc A, theo sơ đồ Ven, ta thấy C ⊂ A. Do đó, C \ A = ∅.
g) D \ A là tập hợp các phần tử thuộc D nhưng không thuộc A, mà D là tập hợp các học sinh nam khối 10 của trường và A là tập hợp các học sinh nữ của trường, do đó D \ A là tập hợp các học sinh nam khối 10 của trường và chính là tập D.
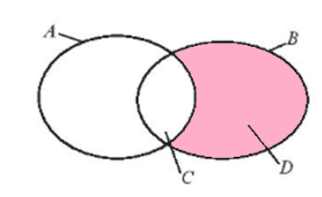
Vậy D \ A = D.
Bài 5 trang 17 SBT Toán 10 Tập 1: Cho A là tập hợp tùy ý. Hãy điền kí hiệu tập hợp thích hợp vào chỗ chấm.
a) A ∩ A = …;
b) A ∪ A = …;
c) A ∩ ∅ = …;
d) A ∪ ∅ = …;
e) A \ A = …;
g) A \ ∅ = …;
h) ∅ \ A = ….
Lời giải:
a) A ∩ A = {x | x ∈ A và x ∈ A} = {x | x ∈ A} = A.
b) A ∪ A = {x | x ∈ A hoặc x ∈ A} = {x | x ∈ A} = A.
c) Do ∅ ⊂ A nên A ∩ ∅ = ∅.
d) Do ∅ ⊂ A nên A ∪ ∅ = A.
e) A \ A = {x | x ∈ A và x ∉ A} = ∅.
g) A \ ∅ = A. (Do tập ∅ không có chứa phần tử nào).
h) ∅ \ A = ∅.
Bài 6 trang 17 SBT Toán 10 Tập 1: Cho A, B là hai tập hợp tùy ý. Hãy điền kí hiệu tập hợp thích hợp vào chỗ chấm.
a) Nếu B ⊂ A thì A ∩ B = …, A ∪ B = … và B \ A = …;
b) Nếu A ∩ B = ∅ thì A \ B = … và B \ A = ….
Lời giải:
a) Ta có B ⊂ A, ta biểu diễn sơ đồ Ven như sau:
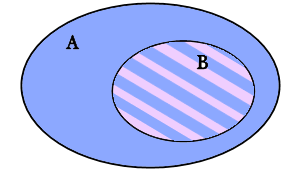
Khi đó, mọi phần tử của B đều là phần tử của A.
Vậy A ∩ B = B, A ∪ B = A và B \ A = ∅.
b) Ta có A ∩ B = ∅ nên A và B là hai tập hợp rời nhau:

Khi đó mọi phần tử của A và B đều khác nhau.
Vậy A \ B = A và B \ A = B.
Bài 7 trang 17 SBT Toán 10 Tập 1: Cho các tập con A = [– 1; 3] và B = [0; 5) của tập số thực ℝ. Hãy xác định A ∩ B, A ∪ B, A \ B, B \ A.
Lời giải:
+ Để xác định A ∩ B ta vẽ sơ đồ sau:
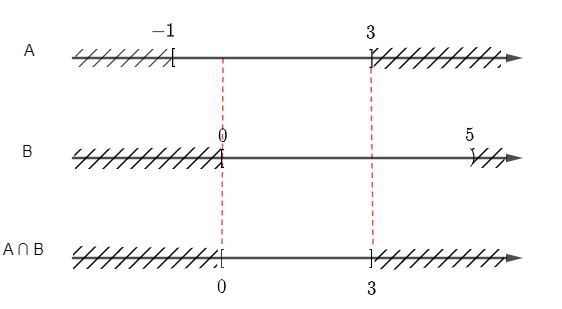
Từ sơ đồ, ta suy ra A ∩ B = [– 1; 3] ∩ [0; 5) = [0; 3].
+ Để xác định A ∪ B ta vẽ sơ đồ sau:
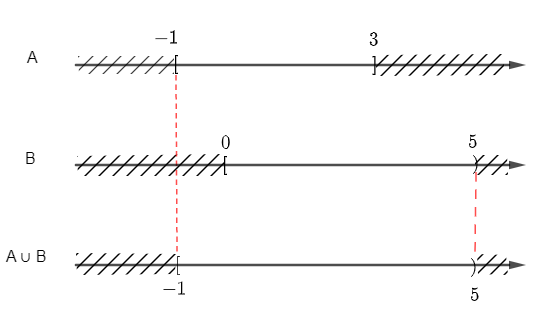
Từ sơ đồ, ta suy ra A ∪ B = [– 1; 3] ∪ [0; 5) = [– 1; 5).
+ Để xác định A \ B ta vẽ sơ đồ sau:
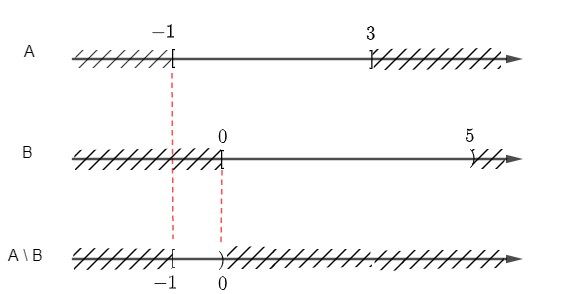
Từ sơ đồ, ta suy ra A \ B = [– 1; 3] \ [0; 5) = [– 1; 0).
+ Để xác định B \ A ta vẽ sơ đồ sau:
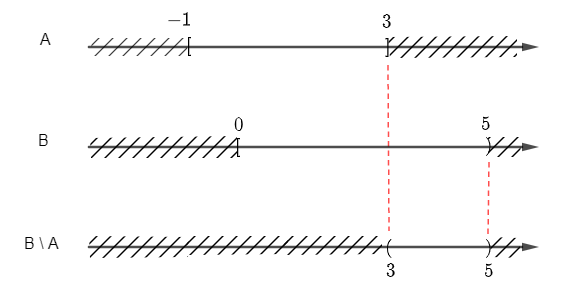
Từ sơ đồ, ta suy ra B \ A = [0; 5) \ [– 1; 3] = (3; 5).
Bài 8 trang 17 SBT Toán 10 Tập 1: 10E có 18 bạn chơi cầu lông, 15 bạn chơi cờ vua, 10 bạn chơi cả hai môn và 12 bạn không chơi môn nào trong hai môn thể thao này.
a) 10E có bao nhiêu bạn chơi ít nhất một môn thể thao trên?
b) 10E có bao nhiêu học sinh?
Lời giải:
Kí hiệu A là tập hợp các học sinh của 10E, B = {x ∈ A | x chơi cầu lông},
C = {x ∈ A | x chơi cờ vua}, D = {x ∈ A |x không chơi cầu lông, cũng không chơi cờ vua}.
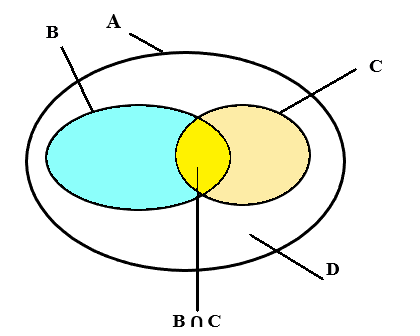
Theo giả thiết, n(B) = 18, n(C) = 15, n(B ∩ C) = 10 và n(D) = 12.
a) Số học sinh của 10E chơi ít nhất một môn thể thao là:
n(B ∪ C) = n(B) + n(C) – n(B ∩ C) = 18 + 15 – 10 = 23 (bạn).
b) Số học sinh của 10E là:
n(A) = n(B ∪ C) + n(D) = 23 + 12 = 35 (bạn).
Bài 9 trang 17 SBT Toán 10 Tập 1: Biết rằng tập hợp M thỏa mãn M ∩ {1; 3} = {1}, M ∩ {5; 7} = {5}, M ∩ {9; 11} = {9} và M ⊂ {1; 3; 5; 7; 9; 11}. Hãy tìm M.
Lời giải:
Do M ∩ {1; 3} = {1}, suy ra 1 ∈ M và 3 ∉ M.
Do M ∩ {5; 7} = {5}, suy ra 5 ∈ M và 7 ∉ M.
Do M ∩ {9; 11} = {9}, suy ra 9 ∈ M và 11 ∉ M.
Lại có M ⊂ {1; 3; 5; 7; 9; 11}.
Do đó, các phần tử của M là 1; 5; 9.
Vậy M = {1; 5; 9}.
Bài 10 trang 17 SBT Toán 10 Tập 1: Cho tập hợp A = {1; 2; 3},
a) tìm tất cả các tập hợp B sao cho A ∪ B = A;
b) tìm tất cả các tập hợp C sao cho A ∩ C = C.
Lời giải:
a) Ta có A ∪ B = A khi và chỉ khi mọi phần tử của B đều là phần tử của A hay B phải là tập con của A.
Mà A = {1; 2; 3}, nên các tập con của A là: ∅, {1}, {2}, {3}, {1; 2}, {1; 3}, {2; 3}, {1; 2; 3}.
Vậy các tập hợp B cần tìm là: ∅, {1}, {2}, {3}, {1; 2}, {1; 3}, {2; 3}, {1; 2; 3}.
b) Ta có A ∩ C = C khi và chỉ khi mọi phần tử của C đều là phần tử của A hay C là tập con của A.
Vậy các tập hợp C cần tìm là: ∅, {1}, {2}, {3}, {1; 2}, {1; 3}, {2; 3}, {1; 2; 3}.
Bài 11 trang 17 SBT Toán 10 Tập 1: Cho U = {3; 5; a2}, A = {3; a + 4}. Tìm giá trị của a sao cho CUA = {1}.
Lời giải:
Ta có: CUA = U \ A = {x | x ∈ U và x ∉ A}.
Mà CUA = {1}, do đó, 1 ∈ U = {3; 5; a2}, suy ra a2 = 1 nên a = 1 hoặc a = – 1.
+ Với a = 1, suy ra a + 4 = 1 + 4 = 5 nên ta có U = {1; 3; 5} và A = {3; 5}.
Khi đó, CUA = U \ A = {1} (thỏa mãn).
+ Với a = – 1, suy ra a + 4 = – 1 + 4 = 3 nên ta có U = {1; 3; 5} và A = {3}.
Khi đó, CUA = U \ A = {1; 5} (không thỏa mãn).
Vậy giá trị cần tìm là a = 1.
Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Tập hợp
Bài tập cuối chương 1
Bài 1: Bất phương trình bậc nhất hai ẩn
Bài 2: Hệ bất phương trình bậc nhất hai ẩn