Lý thuyết Toán lớp 10 Bài 1: Tọa độ của vectơ
A. Lý thuyết Tọa độ của vectơ
1. Tọa độ của vectơ đối với một hệ trục tọa độ
1.1. Trục tọa độ
Trục tọa độ (gọi tắt là trục) là một đường thẳng trên đó đã xác định một điểm O (gọi là điểm gốc) và một vectơ có độ dài bằng 1 gọi là vectơ đơn vị của trục.
Ta kí hiệu trục đó là .
 1.2. Hệ trục tọa độ
1.2. Hệ trục tọa độ
Hệ trục tọa độ gồm hai trục và vuông góc với nhau. Điểm gốc O chung của hai trục gọi là gốc tọa độ. Trục được gọi là trục hoành và kí hiệu là Ox, trục được gọi là trục tung và kí hiệu là Oy. Các vectơ và là các vectơ đơn vị trên Ox và Oy. Hệ trục tọa độ còn được kí hiệu là Oxy.
 Chú ý: Mặt phẳng mà trên đó đã cho một hệ trục tọa độ Oxy được gọi là mặt phẳng tọa độ Oxy, hay gọi tắt là mặt phẳng Oxy.
Chú ý: Mặt phẳng mà trên đó đã cho một hệ trục tọa độ Oxy được gọi là mặt phẳng tọa độ Oxy, hay gọi tắt là mặt phẳng Oxy.
1.3. Tọa độ của một vectơ
Trong mặt phẳng Oxy, cặp số (x; y) trong biểu diễn được gọi là tọa độ của vectơ , kí hiệu , x gọi là hoành độ, y gọi là tung độ của vectơ .
Ví dụ:
+) Cho .
Ta có cặp số (3; 2) là tọa độ của vectơ .
Ta kí hiệu là .
Trong đó: 3 là hoành độ của vectơ và 2 là tung độ của vectơ .
+) Cho .
Ta có cặp số (0; –5) là tọa độ của vectơ .
Ta kí hiệu là .
Trong đó 0 là hoành độ của vectơ và –5 là tung độ của vectơ .
Chú ý:
• .
• Nếu cho và thì .
Ví dụ:
+) Ta có .
+) Ta có và . Khi đó .
Nghĩa là, .
1.4. Tọa độ của một điểm
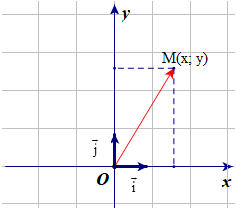
Trong mặt phẳng tọa độ, cho một điểm M tùy ý. Tọa độ của vectơ được gọi là tọa độ của điểm M.
Nhận xét:
• Nếu thì cặp số (x; y) là tọa độ của điểm M, kí hiệu M(x; y), x gọi là hoành độ, y gọi là tung độ của điểm M.
• M(x; y) .
Ví dụ:
+) Nếu thì cặp số (–3; 8) là tọa độ của điểm M.
Ta kí hiệu là M(–3; 8).
Trong đó –3 là hoành độ của điểm M và 8 là tung độ của điểm M.
+) Cho điểm M(4; 9) .
Chú ý: Hoành độ của điểm M còn được kí hiệu là xM, tung độ của điểm M còn được kí hiệu là yM. Khi đó ta viết M(xM; yM).
Ví dụ: Trong mặt phẳng Oxy, cho ba điểm M, N, P được biểu diễn như hình bên.
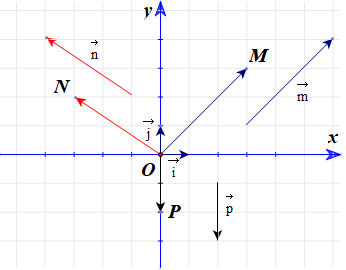
a) Hãy biểu diễn các vectơ qua hai vectơ và .
b) Tìm tọa độ của các vectơ và các điểm M, N, P.
Hướng dẫn giải
a) Ta có:
+) .
+) .
+) .
Vậy , , .
b) Từ kết quả ở câu a), ta có:
+)
và M(3; 3).
+)
và N(–3; 2).
+)
và P(0; –2).
Vậy và M(3; 3), N(–3; 2), P(0; –2).
2. Biểu thức tọa độ của các phép toán vectơ
Cho hai vectơ và số thực k. Khi đó:
(1) ;
(2) ;
(3) ;
(4) .
Ví dụ: Cho hai vectơ .
a) Tìm tọa độ của các vectơ
b) Tính các tích vô hướng , .
Hướng dẫn giải
a) Với ta có:
+) ;
+) ;
+) ;
+) .
Ta suy ra .
Vậy , , , .
b) Với ta có:
+) ;
+) Từ kết quả câu a), ta có và .
Ta suy ra và .
Khi đó ta có .
Vậy và .
3. Áp dụng của tọa độ vectơ
3.1. Liên hệ giữa tọa độ của điểm và tọa độ của vectơ trong mặt phẳng
Cho hai điểm A(xA; yA), B(xB; yB). Ta có: .
Ví dụ: Cho ba điểm A(2; 5), B(–1; 1), C(5; –7). Tìm tọa độ của các vectơ .
Hướng dẫn giải
Với A(2; 5), B(–1; 1), C(5; –7) ta có:
• .
• .
• .
Vậy .
3.2. Tọa độ trung điểm của đoạn thẳng và trọng tâm của tam giác
Cho hai điểm A(xA; yA) và B(xB; yB). Tọa độ trung điểm M(xM; yM) của đoạn thẳng AB là:
.
Cho ∆ABC có A(xA; yA), B(xB; yB), C(xC; yC). Tọa độ trọng tâm G(xG; yG) của tam giác ABC là:
.
Ví dụ: Cho ∆DEF có tọa độ các đỉnh là D(3; 1), E(5; 8), F(9; 4).
a) Tìm tọa độ trung điểm H của cạnh EF.
b) Tìm tọa độ trọng tâm G của ∆DEF.
Hướng dẫn giải
a) Với E(5; 8), F(9; 4):
Vì H là trung điểm của cạnh EF.
Ta suy ra
Vậy H(7; 6).
b) Với D(3; 1), E(5; 8), F(9; 4):
Vì G là trọng tâm của ∆DEF.
Ta suy ra
Vậy .
3.3. Ứng dụng biểu thức tọa độ của các phép toán vectơ
Cho hai vectơ và hai điểm A(xA; yA), B(xB; yB). Ta có:
• ;
• và cùng phương ⇔ a1b2 – a2b1 = 0;
• ;
• ;
• ( khác ).
Ví dụ: Trong mặt phẳng Oxy, cho ∆MNP có M(2; 1), N(–3; –2), P(7; –8).
a) Tìm tọa độ H là chân đường cao của ∆MNP kẻ từ N.
b) Giải tam giác MNP.
Hướng dẫn giải
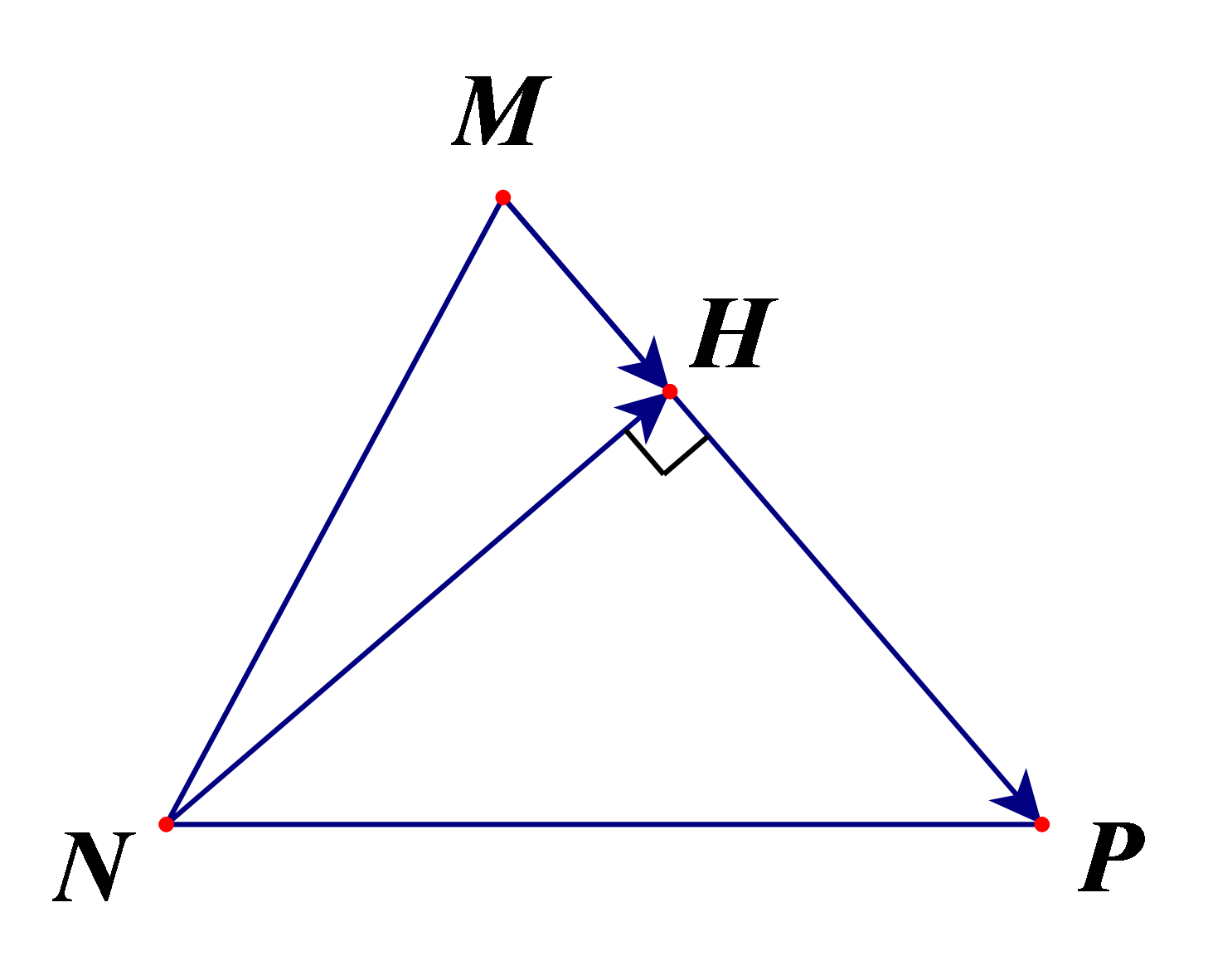 a) Với M(2; 1), N(–3; –2), P(7; –8).
a) Với M(2; 1), N(–3; –2), P(7; –8).
Gọi H(x; y).
Ta có:
+) .
+) .
+)
Vì H(x; y) là chân đường cao của ∆MNP kẻ từ N nên ta có NH ⊥ MP.
Ta suy ra .
Do đó .
⇔ (x + 3).5 + (y + 2).( –9) = 0.
⇔ 5x – 9y – 3 = 0 (1).
Ta thấy hai vectơ cùng phương
⇔ (x – 2).( –9) – (y – 1).5 = 0.
⇔ –9x – 5y + 23 = 0 (2).
Từ (1), (2), ta có hệ phương trình:
Vậy .
b) Với M(2; 1), N(–3; –2), P(7; –8) ta có:
+) và
.
+) . .
+) .
.
+) .
Suy ra .
+) .
Suy ra .
+) Ta có (định lí tổng ba góc của một tam giác).
.
Vậy
B. Bài tập tự luyện
Bài 1. Trong mặt phẳng Oxy, cho , , .
a) Tìm tọa độ các vectơ .
b) Tìm tọa độ của , với .
c) Tìm tọa độ của , với .
d) Tìm các số thực h, k sao cho .
Hướng dẫn giải
a) Ta có:
+) ;
+) ;
+) .
Vậy .
b) Ta có:
+) .
+) .
Ta suy ra .
Khi đó ta có .
Vậy .
c) Ta có .
Khi đó ta có .
Theo đề, ta có: .
.
Vậy .
d) Ta có:
+) ;
+) .
Suy ra .
Ta có .
Vậy thỏa yêu cầu bài toán.
Bài 2. Trong mặt phẳng Oxy, cho ∆ABC biết A(–3; 2), B(4; 3) và điểm C nằm trên trục Ox.
a) Tìm tọa độ trọng tâm G của ∆ABC và điểm C, biết G nằm trên trục Oy.
b) Giải ∆ABC.
c) Tìm tọa độ trực tâm H của ∆ABC.
Hướng dẫn giải
a) Vì C nằm trên trục Ox nên ta có tọa độ C(xC; 0).
Vì G nằm trên trục Oy nên ta có tọa độ G(0; yG).
Ta có G là trọng tâm của ∆ABC.
Ta suy ra
Vậy .
b) Với A(–3; 2), B(4; 3), C(–1; 0) ta có:
+) .
.
+) .
.
+) .
.
+) .
Suy ra .
+)
Do đó cosB .
Suy ra .
+) Ta có (định lí tổng ba góc của một tam giác).
.
Vậy
.
c)
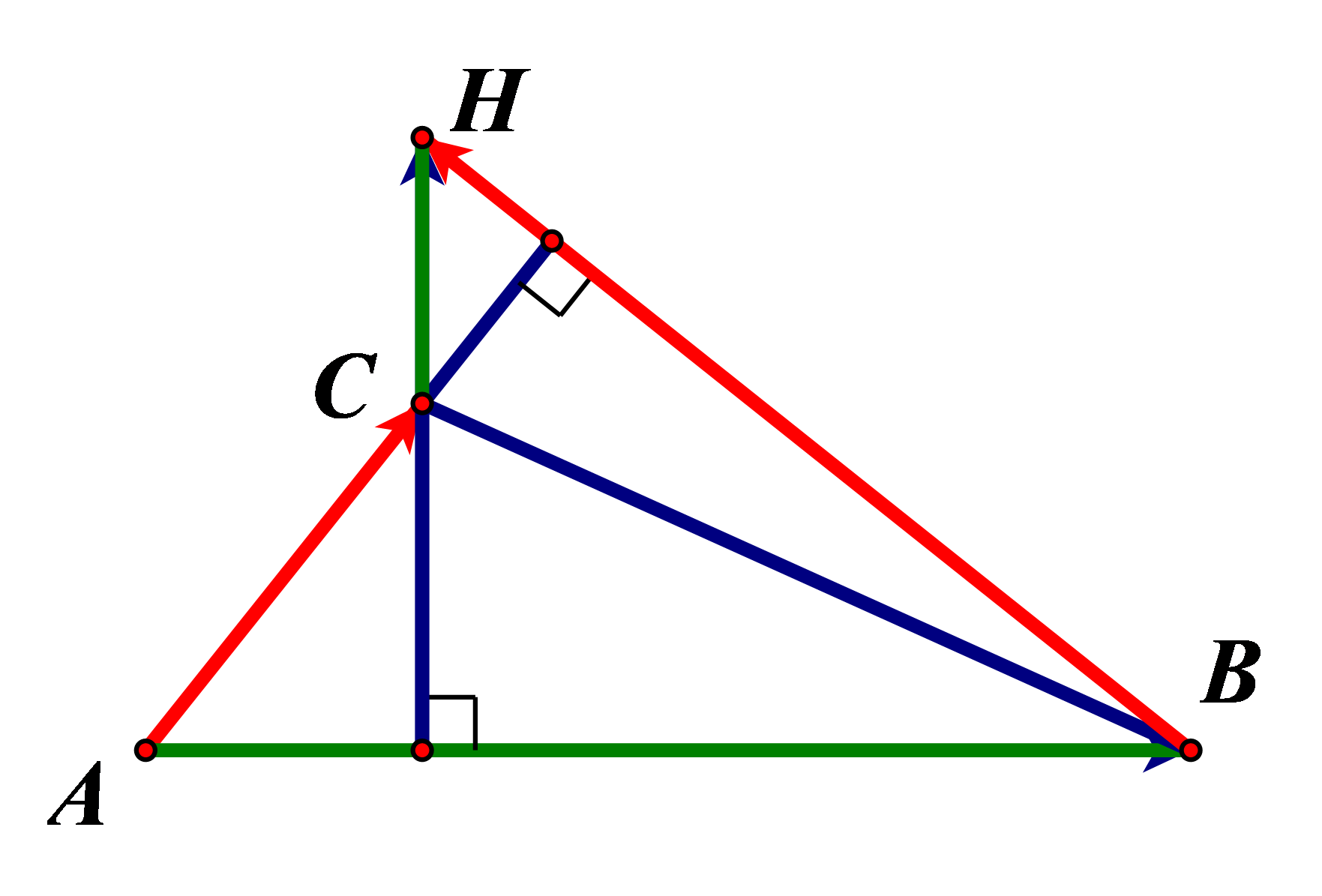 Gọi H(x; y).
Gọi H(x; y).
Þ và .
Ta có H(x; y) là trực tâm của ∆ABC.
Suy ra
Khi đó ta có
Vậy .
Bài 3. Trong mặt phẳng Oxy, cho ba vectơ . Tìm m để cùng phương với
Hướng dẫn giải
Ta có .
Ta suy ra .
Ta có cùng phương với ⇔ (m – 3).5 – (2m + 1).6 = 0.
⇔ –7m – 21 = 0
⇔ m = –3.
Vậy m = –3 thỏa yêu cầu bài toán.
Xem thêm các bài tóm tắt lý thuyết Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 3: Nhị thức Newton
Lý thuyết Bài 1: Tọa độ của vectơ
Lý thuyết Bài 2: Đường thẳng trong mặt phẳng tọa độ
Lý thuyết Bài 3: Đường tròn trong mặt phẳng tọa độ
Lý thuyết Bài 4: Ba đường conic trong mặt phẳng tọa độ