Lý thuyết Tọa độ của vectơ (Cánh diều 2023) hay, chi tiết

Lý thuyết Toán lớp 10 Bài 1: Tọa độ của vectơ

A. Lý thuyết

I. Tọa độ của một điểm

Để xác định tọa độ của một điểm M tùy ý trong mặt phẳng tọa độ Oxy, ta làm như sau (Hình 3):

QUẢNG CÁO

+ Từ M kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm H ứng với số a. Số a là hoành độ của điểm M.

+ Từ M kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm K ứng với số b. Số b là tung độ của điểm M.

Cặp số (a; b) là tọa độ của điểm M trong mặt phẳng tọa độ Oxy. Ta kí hiệu là M(a ; b).

Ví dụ: Xác định tọa độ của điểm B trong hình vẽ sau:

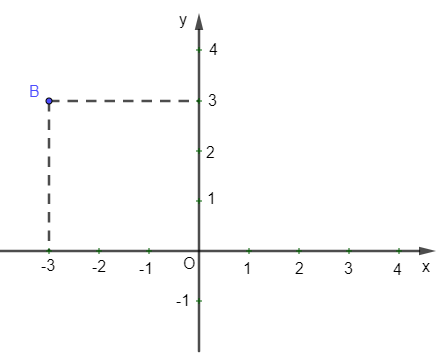
Hướng dẫn giải

+ Từ B kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm ứng với số –3. Số –3 là hoành độ của điểm B.

+ Từ B kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm ứng với số 3. Số 3 là tung độ của điểm M.

Khi đó, cặp số (–3; 3) là tọa độ của điểm B.

Vậy điểm B có tọa độ là B(–3; 3).

QUẢNG CÁO

II. Tọa độ của một vectơ

Tọa độ của điểm M được gọi là tọa độ của vectơ $\vec{O M}$ .

Nếu $\vec{O M}$ có tọa độ (a; b) thì ta viết $\vec{O M}$ = (a; b) hay $\vec{O M}$ (a; b), trong đó a gọi là hoành độ của vectơ $\vec{O M}$ và b gọi là tung độ của vectơ $\vec{O M}$ (Hình 4).

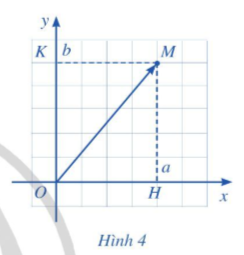
Chú ý: Trong mặt phẳng tọa độ Oxy, ta có:

+ $\vec{O M}$ = (a; b) ⇔ M(a ; b).

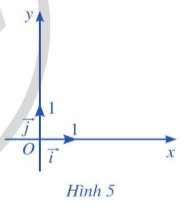
+ Vectơ $\vec{i}$ có điểm gốc là O và có tọa độ (1; 0) gọi là vectơ đơn vị trên trục Ox.

Vectơ $\vec{j}$ có điểm gốc là O và có tọa độ (0; 1) gọi là vectơ đơn vị trên trục Oy (Hình 4).

Ví dụ: Tìm tọa độ của vectơ $\vec{O M}$ , $\vec{O N}$ trong hình sau:

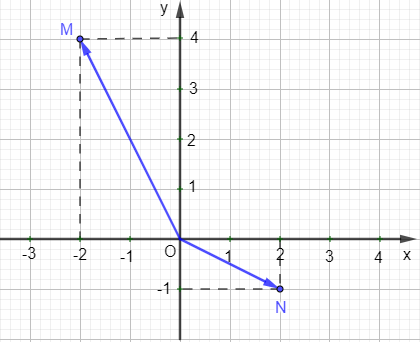
Hướng dẫn giải

Ta thấy điểm M có tọa độ là (–2 ; 4)

Suy ra $\vec{O M}$ = (–2 ; 4).

Điểm N có tọa độ là (2 ; –1)

Suy ra $\vec{O N}$ = (2 ; –1).

Vậy $\vec{O M}$ = (–2 ; 4) và $\vec{O N}$ = (2 ; –1).

Nhận xét:

– Với mỗi vectơ $\vec{u}$ , ta xác định được duy nhất một điểm A sao cho $\vec{O A}$ = $\vec{u}$ .

– Với mỗi vectơ $\vec{u}$ trong mặt phẳng tọa độ Oxy, tọa độ của vectơ $\vec{u}$ là tọa độ của điểm A, trong đó A là điểm sao cho $\vec{O A}$ = $\vec{u}$ .

– Nếu $\vec{u}$ có tọa độ (a; b) thì ta viết $\vec{u}$ = (a; b) hay $\vec{u}$ (a; b), trong đó a gọi là hoành độ của vectơ $\vec{u}$ và b gọi là tung độ của vectơ $\vec{u}$ .

Ví dụ: Tìm tọa độ của vectơ $\vec{u}$ trong hình vẽ sau:

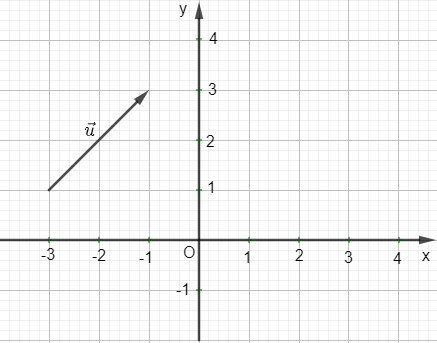
Hướng dẫn giải

Ta xác định vectơ $\vec{u}$ = $\vec{O A}$ như hình sau:

Ta thấy điểm A(2 ; 2) nên $\vec{O A}$ = (2 ; 2).

Suy ra $\vec{u}$ = (2 ; 2).

Vậy $\vec{u}$ = (2 ; 2).

Định lí: Trong mặt phẳng tọa độ Oxy, nếu $\vec{u}$ = (a ; b) thì $\vec{u}$ = a $\vec{i}$ + b $\vec{j}$ . Ngược lại, nếu $\vec{u}$ = a $\vec{i}$ + b $\vec{j}$ thì $\vec{u}$ = (a ; b).

Chú ý: Với $\vec{a}$ = (x₁ ; y₁) và $\vec{b}$ = (x₂ ; y₂), ta có $\vec{a}$ = $\vec{b}$ ⇔ $\{\begin{cases} x_{1} = x_{2} \\ y_{1} = y_{2} \end{cases}$

Như vậy, mỗi vectơ hoàn toàn được xác định khi biết tọa độ của nó.

Ví dụ: Trong mặt phẳng tọa độ Oxy, cho điểm M(2; 3) và vectơ $\vec{u}$ = (1; – 3).

a) Biểu diễn vectơ $\vec{u}$ qua hai vectơ $\vec{i}$ và $\vec{j}$ .

b) Biểu diễn vectơ $\vec{O M}$ qua hai vectơ $\vec{i}$ và $\vec{j}$ .

Hướng dẫn giải

a) Vì vectơ $\vec{u}$ = (1; – 3) nên $\vec{u}$ = 1 $\vec{i}$ + (– 3) $\vec{j}$ = $\vec{i}$ – 3 $\vec{j}$

Vậy $\vec{u}$ = $\vec{i}$ – 3 $\vec{j}$

b) Vì điểm M có tọa độ là (2 ; 3) nên $\vec{O M}$ = (2 ; 3).

Do đó: $\vec{O M}$ = 2 $\vec{i}$ + 3 $\vec{j}$ .

Vậy $\vec{O M}$ = 2 $\vec{i}$ + 3 $\vec{j}$ .

III. Liên hệ giữa tọa độ của điểm và tọa độ của vectơ

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(x_A; y_A) và B(x_B; y_B).

Ta có $\vec{A B}$ = (x_B – x_A ; y_B – y_A).

Ví dụ: Cho hai điểm A(2; –4) và B(1; 5). Hãy tìm tọa độ của vectơ $\vec{A B}$ .

Hướng dẫn giải

Ta có $\vec{A B}$ = (1 – 2; 5 – (–4)) = (–1 ; 9).

Vậy $\vec{A B}$ = (–1 ; 9).

B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Tìm tọa độ của các vectơ sau:

a) $\vec{a}$ = 3 $\vec{i}$ + $\vec{j}$ ;

b) $\vec{b}$ = – 2 $\vec{j}$ ;

c) $\vec{c}$ = $\vec{i}$ – $\sqrt{3}$ $\vec{j}$ .

Hướng dẫn giải

a) Ta có $\vec{a}$ = 3 $\vec{i}$ + $\vec{j}$ = 3 $\vec{i}$ + 1 $\vec{j}$

Suy ra $\vec{a}$ = (3 ; 1).

Vậy $\vec{a}$ = (3 ; 1).

b) Ta có $\vec{b}$ = –2 $\vec{j}$ = 0 $\vec{i}$ + (–2) $\vec{j}$

Suy ra $\vec{b}$ = (0 ; –2).

Vậy $\vec{b}$ = (0 ; –2).

c) Ta có $\vec{c}$ = $\vec{i}$ – $\sqrt{3}$ $\vec{j}$ = $\vec{i}$ + (– $\sqrt{3}$ ) $\vec{j}$ .

Suy ra $\vec{c}$ = (1; – $\sqrt{3}$ ).

Vậy $\vec{c}$ = (1; – $\sqrt{3}$ ).

Bài 2. Cho 3 điểm A(0; 2), B(–1; 3), C(2; 5). Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.

Hướng dẫn giải

Giả sử điểm D có tọa độ là (x_D ; y_D)

Ta có $\vec{A B}$ = (–1 – 0 ; 3 – 2) = (–1 ; 1)

$\vec{D C}$ = (2 – x_D ; 5 – y_D).

Để ABCD là hình bình hành thì $\vec{A B}$ = $\vec{D C}$ .

$\vec{A B}$ = $\vec{D C}$ ⇔ $\{\begin{cases} - 1 = 2 - x_{D} \\ 1 = 5 - y_{D} \end{cases}$ ⇔ $\{\begin{cases} x_{D} = 3 \\ y_{D} = 4 \end{cases}$

Suy ra điểm D có tọa độ là (3 ; 4).

Vậy để ABCD là hình bình hành thì D(3 ; 4).

Bài 3. Tìm số thực m và n sao cho hai vectơ $\vec{a}$ = (m; –4) và $\vec{b}$ = (–1; 3m + n) bằng nhau.

Hướng dẫn giải

Ta có $\vec{a}$ = $\vec{b}$ ⇔ $\{\begin{cases} m = - 1 \\ - 4 = 3 m + n \end{cases}$ ⇔ $\{\begin{cases} m = - 1 \\ - 4 = 3. (- 1) + n \end{cases}$ ⇔ $\{\begin{cases} m = - 1 \\ n = - 1 \end{cases}$

Vậy để $\vec{a}$ = $\vec{b}$ thì m = –1 và n = –1.

B.2 Bài tập trắc nghiệm

Câu 1. Trong hệ tọa độ Oxy cho A(5; 2), B(10; 8). Tìm tọa độ của vectơ $\vec{A B}$ .

A. $\vec{A B}$ = (15; 10);

B. $\vec{A B}$ = (2; 4);

C. $\vec{A B}$ = (5; 6);

D. $\vec{A B}$ = (50; 16).

Hướng dẫn giải

Đáp án đúng là: C

Ta có: $\vec{A B}$ = (10 – 5 ; 8 – 2) = (5; 6).

Câu 2. Trong hệ tọa độ Oxy cho bốn điểm A(1; 1), B(2; – 1), C(4 ; 3), D (3 ; 5). Khẳng định nào sau đây đúng?

A. Tứ giác ABCD là hình bình hành ;

B. A, B, C, D trùng nhau ;

C. $\vec{A B} = \vec{C D};$

D. $\vec{A C}, \vec{A D}$ cùng phương.

Hướng dẫn giải

Đáp án đúng là : A

Ta có : $\{\begin{cases} \vec{A B} = (1; - 2) \\ \vec{D C} = (1; - 2) \end{cases}$ $\Rightarrow$ $\vec{A B} = \vec{D C}$ , do đó ABCD là hình bình hành.

Câu 3. Cho hai vectơ $\vec{u} = (2 a - 1; - 3)$ và $\vec{v} = (3; 4 b + 1)$ . Tìm các số thực a và b sao cho cặp vectơ đã cho bằng nhau:

A. a = 2, b = – 1;

B. a = – 1, b = 2;

C. a = – 1, b = – 2;

D. a = 2, b = 1.

Hướng dẫn giải

Đáp án đúng là: A

Để $\vec{u} = \vec{v} \Leftrightarrow \{\begin{cases} 2 a - 1 = 3 \\ - 3 = 4 b + 1 \end{cases} \Leftrightarrow \{\begin{cases} 2 a = 4 \\ 4 b = - 4 \end{cases} \Leftrightarrow \{\begin{cases} a = 2 \\ b = - 1 \end{cases}$ .

Vậy a = 2 và b = – 1.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 10 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 4: Xác suất của biến cố trong một số trò chơi đơn giản

Lý thuyết Bài 5: Xác suất của biến cố

Lý thuyết Bài 1: Tọa độ của vectơ

Lý thuyết Bài 2: Biểu thức tọa độ của các phép toán vectơ

Lý thuyết Bài 3: Phương trình đường thẳng

Bài liên quan:

Leave a Comment Hủy