Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu bao gồm các nội dung sau:
Phần 1: Tổng hợp các kiến thức cơ bản
Phần 2: Những bài toán cơ bản
Phần 3: 10 bài toán hình học Oxy
Phần 4: Sáng tạo và phát triển từ các bài toán hình học phẳng thuần túy
Phần 5: Bài tập tổng hợp
10 bài toán trọng điểm tuy duy giải nhanh Hình học Oxy
Phần 1: Tổng hợp kiến thức cơ bản
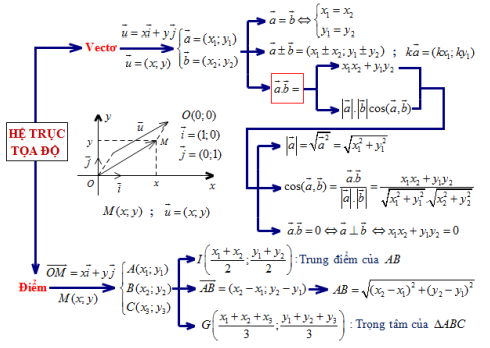
A. Hệ trục tọa độ Oxy hay \((O;\vec i;\vec j)\) có \(\left\{ {\begin{array}{*{20}{l}}{O(0;0)}\\{\vec i = (1;0)}\\{\vec j = (0;1)}\end{array}} \right.\)
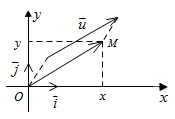
I. Hệ trục tọa độ
Ox: Trục hoành ; Oy : Trục tung
Chú ý:
Nếu nói Oxtới tia hay tia Oy được hiểu là phần hoành độ và tung độ không âm của các trục Ox, Oy tương ứng.
B. Vectơ:
\(\vec u = x\vec i + y\vec j \Leftrightarrow \vec u = (x;y)\)
Cho hai vectơ \(\vec a = \left( {{x_1};{y_1}} \right)\) và \(\vec b = \left( {{x_2};{y_2}} \right)\). Khi đó:
1. Hai vectơ bằng nhau: \(\vec a = \vec b \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = {x_2}}\\{{y_1} = {y_2}}\end{array}} \right.\)
2. Hai vectơ cùng phương \(:\vec a\) và \(\vec b\) cùng phương \( \Leftrightarrow \vec a = k\vec b \Leftrightarrow {x_1}{y_2} = {x_2}{y_1}\)
3. Tổng, hiệu hai vectơ: \(\vec a \pm \vec b = \left( {{x_1} \pm {x_2};{y_1} \pm {y_2}} \right)\)
4. Tích một số với một vectơ: \(k\vec a = \left( {k{x_1};k{y_1}} \right)\)
5. Tích vô hướng của hai vectơ: \(\vec a \cdot \vec b = |\vec a| \cdot |\vec b|\cos (\vec a,\vec b) = {x_1}{x_2} + {y_1}{y_2}\)
6. Môđun của vectơ: \(|\vec a| = \sqrt {x_1^2 + y_1^2} \)
7. Góc giữa hai vectơ: \(\cos (\vec a,\vec b) = \frac{{\vec a \cdot \vec b}}{{|\vec a| \cdot |\vec b|}} = \frac{{{x_1}{x_2} + {y_1}{y_2}}}{{\sqrt {x_1^2 + y_1^2} \cdot \sqrt {x_2^2 + y_2^2} }}\)
8. Hai vectơ vuông góc: \(\vec a \bot \vec b \Leftrightarrow \vec a \cdot \vec b = 0 \Leftrightarrow {x_1}{x_2} + {y_1}{y_2} = 0\)
C. Điểm: \(\overrightarrow {OM} = x\vec i + y\vec j \Leftrightarrow M(x;y)\)
* Cho ba điểm \(A\left( {{x_1};{y_1}} \right),B\left( {{x_2};{y_2}} \right),C\left( {{x_3};{y_3}} \right)\). Khi đó :
1. \(\overrightarrow {AB} = \left( {{x_2} – {x_1};{y_2} – {y_1}} \right)\)
2. \(AB = \sqrt {{{\left( {{x_2} – {x_1}} \right)}^2} + {{\left( {{y_2} – {y_1}} \right)}^2}} \)
3. Trung điểm I của AB có tọa độ: \(I\left( {\frac{{{x_1} + {x_2}}}{2};\frac{{{y_1} + {y_2}}}{2}} \right)\)
4. Trọng tâm G của tam giác \(ABC:G\left( {\frac{{{x_1} + {x_2} + {x_3}}}{3};\frac{{{y_1} + {y_2} + {y_3}}}{3}} \right)\)
Sau đây là sơ đồ cho phần tổng hợp kiến thức trên:
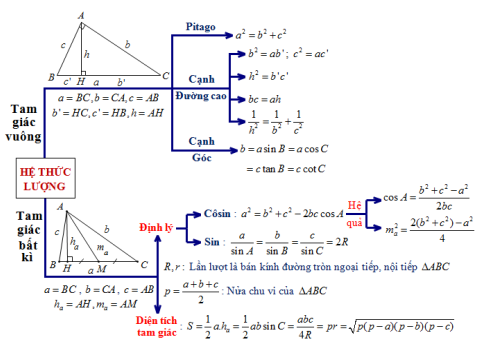
II. Các hệ thức lượng trong tam giác
A. Trong tam giác vuông :
1. Hệ thức Pitago: \({a^2} = {b^2} + {c^2}\)
2. Mối quan hệ giữa cạnh, đường cao:
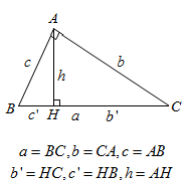
\( + \left\{ {\begin{array}{*{20}{l}}{{b^2} = a{b^\prime }}\\{{c^2} = a{c^\prime }}\end{array}} \right.\)
\( + \frac{1}{{{h^2}}} = \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\)
\( + {h^2} = {b^\prime }{c^\prime }\)
\(a = BC,b = CA,c = AB\)
\( + bc = ah\)
\({b^\prime } = HC,{c^\prime } = HB,h = AH\)
3. Mối quan hệ giữa cạnh và góc:
\(b = a\sin B = a\cos C = c\tan B = c\cot C\)
B. Trong tam giác bất kì
1. Các định lý
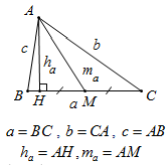
\( \Rightarrow \) Hệ quả:
+ Tính góc:
\({\rm{ }}\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}\)
+ Tính độ dài đường trung tuyến: \(m_a^2 = \frac{{{b^2} + {c^2}}}{2} – \frac{{{a^2}}}{4}\)
* Đinh lý sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
2. Các công thức tính diện tích tam giác
+ Đường cao và cạnh đối diện: \(S = \frac{1}{2}a \cdot {h_a}\)
+ Hai cạnh và sin góc xen giữa: \(S = \frac{1}{2}ab\sin C\)
+ Ba cạnh và bán kính đường tròn ngoại tiếp: \(S = \frac{{abc}}{{4R}}\)
+ Nửa chu vi và bán kính đường tròn nội tiếp: \(S = pr\)
+ Hê – rông: \(S = \sqrt {p(p – a)(p – b)(p – c)} \)
Trong đó:
R là bán kính đường tròn ngoại tiếp tam giác ABC;
r là bán kính đường tròn nội tiếp tam giác ABC;
\(p = \frac{{a + b + c}}{2}\) là nửa chu vi tam giác ABC.
Sau đây là sơ đồ cho phần tổng hợp kiến thức trên:
CÁC HÊ THỨC LƯỢNG TRONG TAM GIÁC
III. Điểm, đường thẳng, đường tròn và elip
A. Điểm
Các điểm đặc biệt của tam giác:
+ Trực tâm : Là giao 3 đường cao của tam giác.
+ Trọng tâm: Là giao 3 đường trung tuyến của tam giác.
+ Tâm đường tròn ngoại tiếp: Là giao 3 đường trung trực của tam giác.
+ Tâm đường tròn nội tiếp: Là giao của 3 đường phân giác trong.
Chú ý:
+ Do giao của các đường (cùng tên) đồng quy, nên khi vẽ hình ta chỉ cần xác định giao của hai đường, thậm chí là một đường nếu đó là trung tuyến (dựa vào tỉ lệ trọng tâm).
+ Tâm đường tròn bàng tiếp : Là giao của 2 đường phân giác ngoài của hai góc hoặc một phân giác ngoài của một góc và một phân giác trong của một góc. Như vậy một tam giác có 3 đường tròn bàng tiếp.
Nếu cho 3 điêm phân biệt \(A\left( {{x_1};{y_1}} \right),B\left( {{x_2};{y_2}} \right),C\left( {{x_3};{y_3}} \right)\), ta có :
\(\overrightarrow {AB} = \left( {{x_2} – {x_1};{y_2} – {y_1}} \right)\) và \(AB = \sqrt {{{\left( {{x_2} – {x_1}} \right)}^2} + {{\left( {{y_2} – {y_1}} \right)}^2}} \)
I là trung điểm của \(AB \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_I} = \frac{{{x_1} + {x_2}}}{2}}\\{{y_I} = \frac{{{y_1} + {y_2}}}{2}}\end{array}} \right.\)
G là trọng tâm của \(\Delta ABC \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_G} = \frac{{{x_1} + {x_2} + {x_3}}}{3}}\\{{y_G} = \frac{{{y_1} + {y_2} + {y_3}}}{3}}\end{array}} \right.\)
A,B,C thẳng hàng \( \Leftrightarrow \exists k \ne 0:\overrightarrow {AB} = k\overrightarrow {AC} \)

B. Đường thẳng
1. Đường thẳng
* Đi qua điêm \(M\left( {{x_0};{y_0}} \right)\) và có :
+ Hệ số góc k có phương trình: \(y = k\left( {x – {x_0}} \right) + {y_0}\).
+ vectơ pháp tuyến (vtpt) \(\vec n = (a;b)\) có phương trình: \(a\left( {x – {x_0}} \right) + b\left( {y – {y_0}} \right) = 0.\)
+ vectơ chỉ phương (vtcp) \(\vec n = (a;b)\) có phương trình dạng tham số là: \(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + at}\\{y = {y_0} + bt}\end{array}} \right.\) hoặc phương trình dạng chính tắc là: \(\frac{{x – {x_0}}}{a} = \frac{{y – {y_0}}}{b}\) (với \(ab \ne 0)\).
Cắt trục Ox, Oy lần lượt tại hai điểm A (a;0); B(0;b) có phương trình đoạn chắn:
\[\frac{x}{a} + \frac{y}{b} = 1{\rm{\;}}\] (với \[{\rm{\;}}ab \ne 0{\rm{\;)}}{\rm{.\;}}\]
Xem thêm