Lý thuyết Hai mặt phẳng vuông góc (Kết nối tri thức 2024) hay, chi tiết | Toán lớp 11

Lý thuyết Toán lớp 11 Bài 25: Hai mặt phẳng vuông góc

A. Lý thuyết Hai mặt phẳng vuông góc

1. Góc giữa hai mặt phẳng, hai mặt phẳng vuông góc

– Cho hai mặt phẳng (P) và (Q). Lấy các đường thẳng a, b tương ứng vuông góc với (P), (Q). Khi đó, góc giữa a và b không phụ thuộc vào vị trí của a, b và được gọi là góc giữa hai mặt phẳng (P) và (Q).

– Hai mặt phẳng (P) và (Q) được gọi là vuông góc với nhau nếu góc giữa chúng bằng ${90}^0$.

Chú ý: Nếu $\phi$ là góc giữa hai mặt phẳng (P) và (Q) thì $0^0\le \phi \le {90}^0$.

Nhận xét:

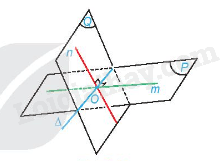
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến $\mathrm{\Delta }$. Lấy hai đường thẳng m, n tương ứng thuộc (P), (Q) và cùng vuông góc với $\mathrm{\Delta }$ tại một điểm O (nói cách khác, lấy một mặt phẳng vuông góc với $\mathrm{\Delta }$, cắt (P), (Q) tương ứng theo các giao tuyến m, n). Khi đó, góc giữa (P) và (Q) bằng góc giữa m và n. Đặc biệt, (P) vuông góc với (Q) khi và chỉ khi m vuông góc với n.

2. Điều kiện để hai mặt phẳng vuông góc

Hai mặt phẳng vuông góc với nhau nếu mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

3. Tính chất của hai mặt phẳng vuông góc

– Với hai mặt phẳng vuông góc với nhau, bất kì đường thẳng nào nằm trong mặt phẳng này mà vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.

Nhận xét: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Mỗi đường thẳng qua điểm O thuộc (P) và vuông góc với mặt phẳng (Q) thì đường thẳng đó thuộc mặt phẳng (P).

– Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.

4. Góc nhị diện

– Hình gồm hai nửa mặt phẳng (P), (Q) có chung bờ a được gọi là một góc nhị diện, kí hiệu là [P,a,Q]. Đường thẳng a và các nửa mặt phẳng (P), (Q) tương ứng được gọi là cạnh và các mặt của góc nhị diện đó.

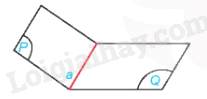
Mỗi đường thẳng a trong một mặt phẳng chia mặt phẳng thành hai phần, mỗi phần cùng với a là một nửa mặt phẳng bờ a.

– Từ một điểm O bất kì thuộc cạnh a của góc nhị diện [P,a,Q], vẽ các tia Ox, Oy tương ứng thuộc (P), (Q) và vuông góc với a. Góc xOy được gọi là một góc phẳng của góc nhị diện [P,a,Q] (gọi tắt là góc phẳng nhị diện). Số đo của góc xOy không phụ thuộc vào vị trí của O trên a, được gọi là số đo của góc nhị diện [P,a,Q].

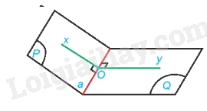
Mặt phẳng chứa góc phẳng nhị diện xOy của [P,a,Q] vuông góc với cạnh a.

Chú ý:

– Số đo của góc nhị diện có thể nhận giá trị từ $0^0$ đến ${180}^0$. Góc nhị diện được gọi là góc vuông, nhọn, tù nếu nó có số đo tương ứng bằng, nhỏ hơn, lớn hớn ${90}^0$.

– Đối với hai điểm M, N không thuộc đường thẳng a, ta kí hiệu [M, a, N] là góc nhị diện có cạnh a và các mặt tương ứng chứa M, N.

– Hai mặt phẳng cắt nhau tạo thành bốn góc nhị diện. Nếu một trong bốn góc nhị diện đó là góc nhị diện vuông thì các góc nhị diện còn lại cũng là góc nhị diện vuông.

5. Một số hình lăng trụ đặc biệt

a) Hình lăng trụ đứng

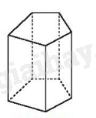
Hình lăng trụ đứng  là hình lăng trụ có các cạnh bên vuông góc với mặt đáy.

Hình lăng trụ đứng có các mặt bên là các hình chữ nhật và vuông góc với mặt đáy.

b) Hình lăng trụ đều

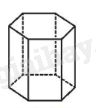
Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.

Hình lăng trụ đều có các mẳ bên là các hình chữ nhật có cùng kích thước.

c) Hình hộp đứng

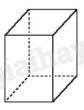
Hình hộp đứng là hình lăng trụ đứng, có đáy là hình bình hành.

Hình hộp đứng có các mặt bên là các hình chữ nhật.

d) Hình hộp chữ nhật

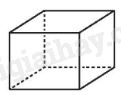
Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.

Hình hộp chữ nhật có các mặt bên là hình chữ nhật. Các đường chéo của hình hộp chữ nhật có độ dài bằng nhau và chúng cắt nhau tại trung điểm của mỗi đường.

e) Hình lập phương

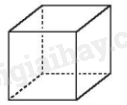
Hình lập phương là hình hộp chữ nhật có tất cả các cạnh bằng nhau,

Hình lập phương có các mặt là các hình vuông.

Chú ý: Khi đáy của hình lăng trụ đứng (đều) là tam giác, tứ giác, ngũ giác,… đôi khi ta cũng tương ứng gọi rõ là hình lăng trụ đứng (đều) tam giác, tứ giác, ngũ giác,…

6. Hình chóp đều và hình chóp cụt đều

Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên bằng nhau.

Chú ý: Tương tự như đối với hình chóp, khi đáy của hình chóp đều là tam giác đều, hình vuông, ngũ giác đều,… đôi khi ta cũng gọi rõ chúng tương ứng là chóp tam giác đều, tứ giác đều, ngũ giác đều,…

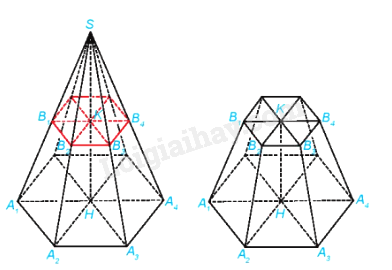
Hình gồm các đa giác đều$A_1{A}_2\dots A_n.B_1{B}_2\dots B_n$ và các hình thang cân $A_1{A}_2{B}_2{B}_1,A_2{A}_3{B}_3{B}_2,\dots ,A_n{A}_1{B}_1{B}_n$ được gọi là một hình chóp cụt đều (nói đơn giản là hình chóp cụt được tạo thành từ hình chóp đều $S.A_1{A}_2\dots A_n$ sau khi cắt đi chóp đều $S\cdot B_1{B}_2\dots B_n$), kí hiệu là $A_1{A}_2\dots A_n\cdot B_1{B}_2\dots B_n$.

– Các đa giác $A_1{A}_2\dots A_n,B_1{B}_2\dots B_n$ được gọi là hai mặt đáy,

– Các hình thang $A_1{A}_2{B}_2{B}_1,A_2{A}_3{B}_3{B}_2,\dots ,A_n{A}_1{B}_1{B}_n$ được gọi là các mặt bên;

– Các đoạn thẳng $A_1{B}_1,A_2{B}_2,\dots ,A_n{B}_n$ được gọi là các cạnh bên;

– Các cạnh của hai mặt đáy được gọi là các cạnh đáy của hình chóp cụt.

Đoạn thẳng HK nối hai tâm của đáy được gọi là đường cao của hình chóp cụt đều. Độ dài của đường cao được gọi là chiều cao của hình chóp cụt.

Sơ đồ tư duy Hai mặt phẳng vuông góc

B. Bài tập Hai mặt phẳng vuông góc

Đang cập nhật …

Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng

Lý thuyết Bài 25: Hai mặt phẳng vuông góc

Lý thuyết Bài 26: Khoảng cách

Lý thuyết Bài 27: Thể tích

Lý thuyết Bài 28: Biến cố hợp, biến cố giao, biến cố độc lập