Câu hỏi:
Cho hình vẽ.
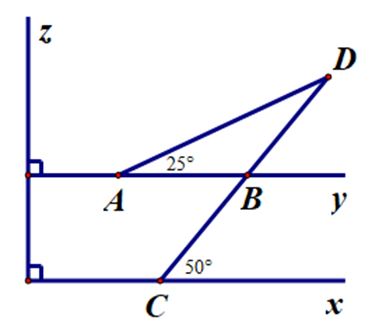
Tam giác cân trong hình vẽ bên là:
A. ∆ACD;
B. ∆ABD;
Đáp án chính xác
C. ∆BCD;
D. Hình vẽ bên không có tam giác nào cân.
Trả lời:
Đáp án đúng là: B
Ta thấy x ⊥ z và y ⊥ z (giả thiết).
Suy ra x // y.
Có \(\widehat {ABC},\,\,\widehat {BCx}\) ở vị trí so le trong.
Do đó \(\widehat {ABC} = \widehat {BCx} = 50^\circ \).
Ta có \(\widehat {ABC} + \widehat {ABD} = 180^\circ \) (hai góc kề bù).
Suy ra \(\widehat {ABD} = 180^\circ – \widehat {ABC} = 180^\circ – 50^\circ = 130^\circ \).
Xét ∆ABD, có: \(\widehat {ABD} + \widehat {BAD} + \widehat {ADB} = 180^\circ \).
Suy ra \(\widehat {ADB} = 180^\circ – \widehat {ABD} – \widehat {BAD} = 180^\circ – 130^\circ – 25^\circ = 25^\circ \).
Do đó \(\widehat {ADB} = \widehat {BAD}\).
Khi đó ta được ∆ABD cân tại B.
Do đó đáp án B đúng.
Đáp án A sai vì \(\widehat {ADB} = 25^\circ \) nên ∆ACD không phải là tam giác đều.
Đáp án C sai vì ba điểm B, C, D là ba điểm thẳng hàng nên không thể tạo thành một tam giác.
Đáp án D sai vì ta đã chứng minh được hình vẽ có ∆ABD cân tại B.
Vậy ta chọn đáp án B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình vẽ bên.
Hình bên có bao nhiêu tam giác cân?
Câu hỏi:
Cho hình vẽ bên.
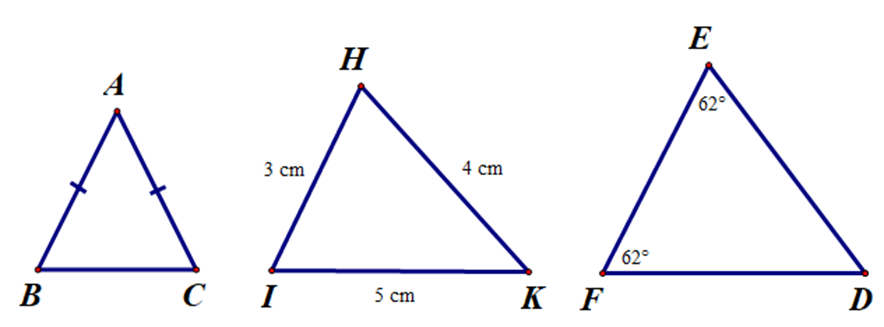
Hình bên có bao nhiêu tam giác cân?
A. 0;
B. 1;
C. 2;
Đáp án chính xác
D. 3.
Trả lời:
Đáp án đúng là: C
Xét ∆ABC có: AB = AC (giả thiết).
Suy ra ∆ABC cân tại A.
Xét ∆HIK có: HI ≠ IK ≠ HK (vì 3 cm ≠ 5 cm ≠ 4 cm).
Do đó ∆HIK không phải là tam giác cân.
Xét ∆DEF có: \(\widehat {DEF} = \widehat {DFE} = 62^\circ \).
Suy ra ∆DEF cân tại D.
Khi đó hình trên có 2 tam giác cân là: ∆ABC và ∆DEF.
Vậy ta chọn đáp án C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Chọn phát biểu sai trong các phát biểu sau.
Câu hỏi:
Chọn phát biểu sai trong các phát biểu sau.
A. Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó có ba cạnh bằng nhau;
B. Để nhận biết và chứng minh một tam giác là tam giác cân, ta cần chứng minh tam giác đó hai góc bằng nhau;
C. Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó có một góc bằng 60°;
Đáp án chính xác
D. Để nhận biết và chứng minh một tam giác là tam giác cân, ta cần chứng minh tam giác đó có hai góc bằng nhau.
Trả lời:
Đáp án đúng là: C
Đáp án A, B, D đúng.
Đáp án C sai. Sửa lại:
Cách sửa 1: Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó có hai góc bằng 60°;
Cách sửa 2: Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó là một tam giác cân và có một góc bằng 60°.
Vậy ta chọn đáp án C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ∆ABC cân tại A. Trên cạnh BC lấy các điểm M, N sao cho BM = CN. Kết luận nào sau đây là đúng?
Câu hỏi:
Cho ∆ABC cân tại A. Trên cạnh BC lấy các điểm M, N sao cho BM = CN. Kết luận nào sau đây là đúng?
A. ∆AMN cân tại A;
Đáp án chính xác
B. ∆AMN cân tại M;
C. ∆AMN cân tại N;
D. ∆AMN cân tại B.
Trả lời:
Đáp án đúng là: A
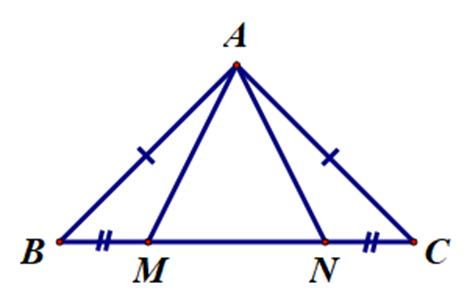
Vì ∆ABC cân tại A nên ta có AB = AC và \(\widehat {ABC} = \widehat {ACB}\).
Xét ∆ABM và ∆ACN, có:
AB = AC (chứng minh trên).
\(\widehat {ABC} = \widehat {ACB}\) (chứng minh trên).
BM = CN (giả thiết).
Do đó ∆ABM = ∆ACN (cạnh – góc – cạnh).
Suy ra AM = AN (cặp cạnh tương ứng).
Do đó ∆AMN cân tại A.
Vậy ta chọn đáp án A.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình bên.
Chọn đáp án đúng.
Câu hỏi:
Cho hình bên.

Chọn đáp án đúng.
A. ∆OPM và ∆ONQ là các tam giác đều;
B. ∆OMN là tam giác đều;
C. ∆OPM và ∆ONQ là các tam giác cân;
D. Cả hai đáp án B, C đều đúng.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D
Quan sát hình, ta thấy OM = ON = MN.
Do đó ∆OMN là tam giác đều.
Quan sát hình, ta thấy OM = PM.
Do đó ∆OPM là tam giác cân tại M.
Quan sát hình, ta thấy ON = NQ.
Do đó ∆ONQ là tam giác cân tại N.
Khi đó ta có: ∆OMN là tam giác đều; ∆OPM và ∆ONQ là các tam giác cân.
Do đó đáp án B, C đều đúng.
Vậy ta chọn đáp án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- \(\widehat {xOy} = 120^\circ \). Lấy điểm A thuộc tia phân giác của \(\widehat {xOy}\). Kẻ AB ⊥ Ox tại B, AC ⊥ Oy tại C. Hỏi ∆ABC là tam giác gì?
Câu hỏi:
\(\widehat {xOy} = 120^\circ \). Lấy điểm A thuộc tia phân giác của \(\widehat {xOy}\). Kẻ AB ⊥ Ox tại B, AC ⊥ Oy tại C. Hỏi ∆ABC là tam giác gì?
A. ∆ABC là tam giác cân tại A;
B. ∆ABC là tam giác cân tại B;
C. ∆ABC là tam giác là cân tại C;
D. ∆ABC là tam giác đều.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D

Xét ∆OAB và ∆OAC, có:
\(\widehat {ACO} = \widehat {ABO} = 90^\circ \).
OA là cạnh chung.
\(\widehat {AOC} = \widehat {AOB}\) (OA là phân giác của \(\widehat {xOy}\)).
Do đó ∆OAB = ∆OAC (cạnh huyền – góc nhọn).
Suy ra AB = AC (cặp cạnh tương ứng).
Do đó ∆ABC cân tại A (1).
Ta có OA là phân giác của \(\widehat {xOy}\).
Suy ra \(\widehat {BOA} = \widehat {AOC} = \frac{{120^\circ }}{2} = 60^\circ \).
∆OAB vuông tại B: \(\widehat {BOA} + \widehat {OAB} = 90^\circ \).
Suy ra \(\widehat {OAB} = 90^\circ – \widehat {BOA} = 90^\circ – 60^\circ = 30^\circ \).
Chứng minh tương tự, ta được \(\widehat {OAC} = 30^\circ \).
Do đó ta có \(\widehat {OAB} + \widehat {OAC} = 30^\circ + 30^\circ = 60^\circ \).
Ta suy ra \(\widehat {BAC} = 60^\circ \) (2).
Từ (1), (2), ta suy ra ∆ABC là tam giác đều.
Vậy ta chọn đáp án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====