Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm, AE = 4 cm. Khẳng định đúng là:

Câu hỏi:

Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm, AE = 4 cm. Khẳng định đúng là:

A. HG = 4 cm, HE = 2 cm, GC = 4 cm;

Đáp án chính xác

B. HG = 2 cm, HE = 2 cm, GC = 4 cm;

C. HG = 4 cm, HE = 2 cm, GC = 2 cm;

D. HG = 4 cm, HE = 4 cm, GC = 4 cm.

Trả lời:

Đáp án đúng là: A

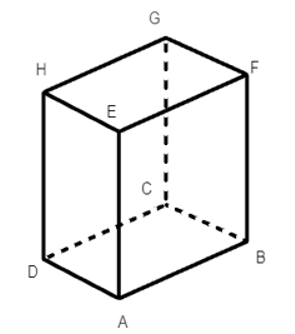
Từ hình hộp chữ nhật ABCD.EFGH ta có các mặt của hình hộp này đều là hình chữ nhật.
Khi đó ta có:
HG = DC = AB = 4 cm;
HE = DA = BC = 2 cm;
GC = HD = AE = 4 cm.
Vậy HG = 4 cm, HE = 2 cm, GC = 4 cm.
Ta chọn đáp án A.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong các câu sau, câu nào đúng?
   
   

   Câu hỏi:
   

   Trong các câu sau, câu nào đúng?

   A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương;

   Đáp án chính xác

   B. Số 0 là số hữu tỉ dương;

   C. Số nguyên âm không phải là số hữu tỉ âm;

   D. Tập hợp ℚ gồm các số hữu tỉ dương và các số hữu tỉ âm.

   Trả lời:

   Đáp án đúng là: A
   Số hữu tỉ âm nhỏ hơn số hữu tỉ dương. Đúng.
   Số 0 là số hữu tỉ dương. Sai vì số hữu tỉ 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.
   Số nguyên âm không phải là số hữu tỉ âm. Sai vì mỗi số nguyên là một số hữu tỉ.
   Tập hợp ℚ gồm các số hữu tỉ dương và các số hữu tỉ âm. Sai vì tập hợp ℚ gồm các số hữu tỉ dương, số 0 và các số hữu tỉ âm.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

2. Số đối của số hữu tỉ 94 là
   
   

   Câu hỏi:
   

   Số đối của số hữu tỉ $\frac{9}{4}$ là

   A. $–\frac{9}{4}$;

   Đáp án chính xác

   B.$\frac{–9}{–4}$;

   C. $\frac{4}{9}$;

   D. $\frac{–4}{9}$ .

   Trả lời:

   Đáp án đúng là: A
   Số đối của số hữu tỉ $\frac{9}{4}$ là $–\frac{9}{4}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

3. Cho a = 2−9 và b = -13. Khẳng định nào sau đây là đúng?
   
   

   Câu hỏi:
   

   Cho a = $\frac{2}{-9}$ và b = $\frac{–1}{3}$.
   Khẳng định nào sau đây là đúng?

   A. a = b;

   B. a > b;

   Đáp án chính xác

   C. a < b;

   D. a ≤ b.

   Trả lời:

   Đáp án đúng là: B
   Ta có:
   $\frac{2}{-9}=\frac{-2}{9}$
   $\frac{-1}{3}=\frac{\left(-1\right).3}{3.3}=\frac{-3}{9}$ (quy đồng mẫu số)
   Vì ‒2 > ‒3 nên $\frac{-2}{9}>\frac{-3}{9}$
   Hay $\frac{2}{-9}$ > $\frac{–1}{3}$.
   Vậy $\frac{2}{-9}$ > $\frac{–1}{3}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

4. Cho các điểm A, B, C, D biểu diễn các số trên trục số như sau: Điểm biểu diễn số 6−4 là:
   
   

   Câu hỏi:
   

   Cho các điểm A, B, C, D biểu diễn các số trên trục số như sau:
   
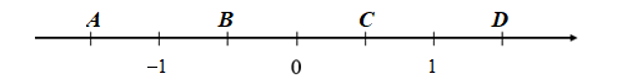
   Điểm biểu diễn số $\frac{6}{-4}$ là:

   A. Điểm A;

   Đáp án chính xác

   B. Điểm B;

   C. Điểm C;

   D. Điểm D.

   Trả lời:

   Đáp án đúng là: A
   
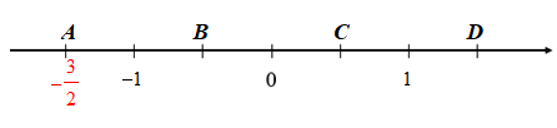
   Ta thấy đoạn thẳng đơn vị (chẳng hạn từ 0 đến 1) được chia thành 2 phần bằng nhau, ta lấy một đoạn làm đơn vị mới, đơn vị mới bằng  đơn vị cũ.
   Số hữu tỉ $\frac{6}{-4}=-\frac{3}{2}$  được biểu diễn bởi điểm nằm bên trái điểm 0 và cách 0 một đoạn bằng 3 đơn vị mới (hình vẽ trên). Điểm này chính là điểm A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

5. Cho biểu thức 21+154:38−16.57. Chọn khẳng định đúng?
   
   

   Câu hỏi:
   

   Cho biểu thức $21+\frac{15}{4}:\left(\frac{3}{8}-\frac{1}{6}\right).\frac{5}{7}$. Chọn khẳng định đúng?

   A. Ta cần thực hiện phép tính trừ trước;

   Đáp án chính xác

   B. Ta cần thực hiện phép chia trước;

   C. Ta cần thực hiện phép nhân trước;

   D. Ta cần thực hiện phép cộng trước.

   Trả lời:

   Đáp án đúng là: A
   Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau.
   Vì các phép tính cộng, nhân, chia ở ngoài ngoặc và phép tính trừ ở trong ngoặc, nên ta thực hiện phép tính trừ trước.
   Vậy ta chọn phương án A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====