Câu hỏi:
Cho tam giác ABC:
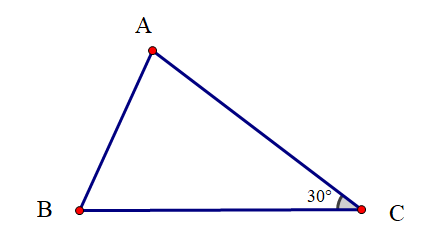
Vẽ đường thẳng m đi qua A và song song với BC?
A.
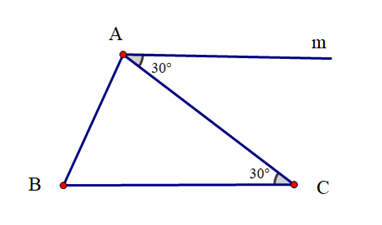 ;
;
Đáp án chính xác
B.
 ;
;
C.
 ;
;
D.
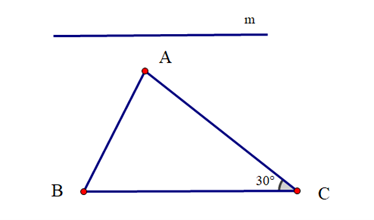 .
.
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: A
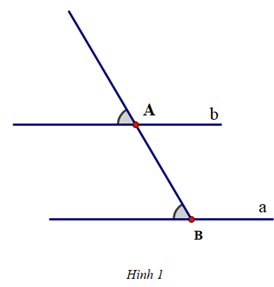
Hình A cho thấy đường thẳng m đi qua A. Đồng thời m // AB vì có hai góc ở vị trí đồng vị đều bằng 30°.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đường thẳng y và điểm M nằm ngoài đường thẳng y như hình vẽ:
Vẽ đường thẳng x qua M và song song với đường thẳng y.
Câu hỏi:
Cho đường thẳng y và điểm M nằm ngoài đường thẳng y như hình vẽ:
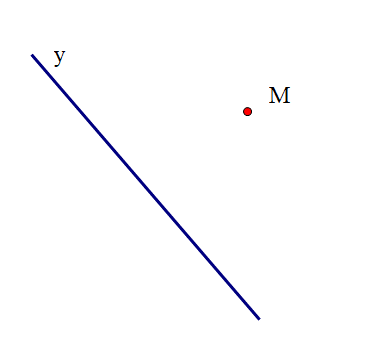
Vẽ đường thẳng x qua M và song song với đường thẳng y.Trả lời:
Hướng dẫn giải:
Để vẽ đường thẳng x qua M và song song với đường thẳng y, ta làm như sau:
+ Đặt thước kẻ sao cho chiều rộng của thước kẻ nằm trên đường thẳng y, chiều dài đi qua điểm M.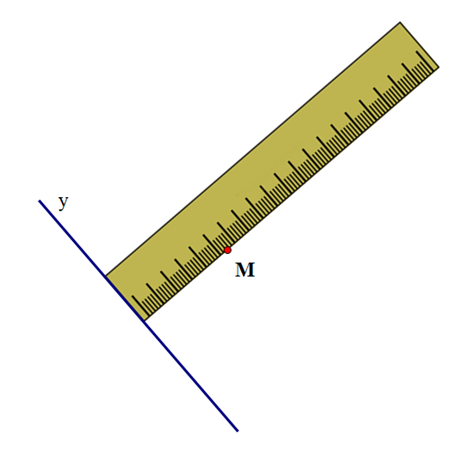
+ Vẽ theo cạnh đi qua điểm M của thước kẻ đường thẳng d
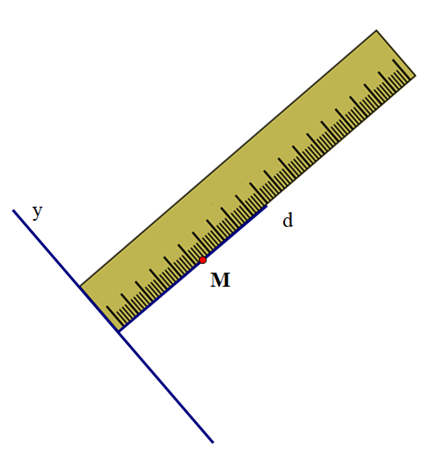
+ Đặt thước kẻ sao cho một vạch chia trên thước trùng với đường thẳng d và cạnh của thước đi qua điểm M
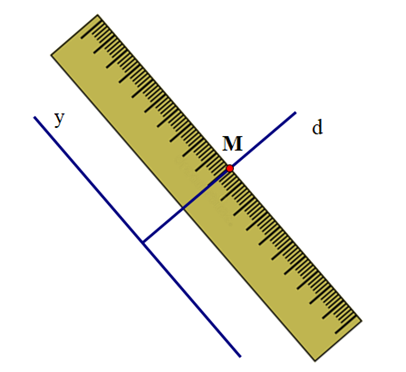
+ Vẽ theo cạnh đi qua điểm M của thước kẻ đường thẳng x
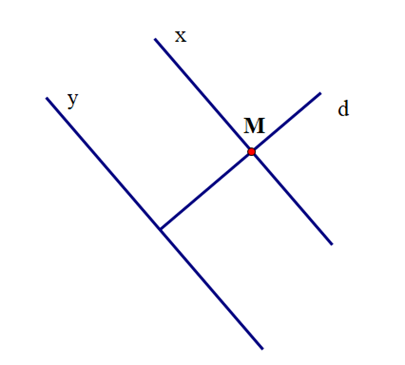
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho các hình vẽ sau:
Để vẽ đường thẳng b đi qua A và song song với đường thẳng a cho trước, ta thực hiện theo thứ tự nào sau đây:
Câu hỏi:
Cho các hình vẽ sau:
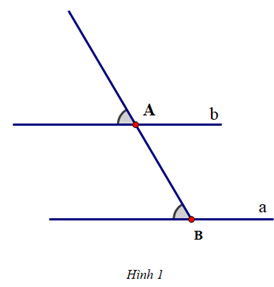
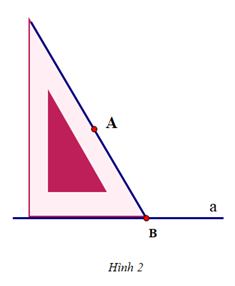


Để vẽ đường thẳng b đi qua A và song song với đường thẳng a cho trước, ta thực hiện theo thứ tự nào sau đây:A. Hình 5 – Hình 1 – Hình 2 – Hình 3 – Hình 4;
B. Hình 5 – Hình 2 – Hình 3 – Hình 4 – Hình 1;
C. Hình 5 – Hình 2 – Hình 4 – Hình 3 – Hình 1;
Đáp án chính xác
D. Hình 5 – Hình 2 – Hình 1 – Hình 3 – Hình 4.
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: C
Để vẽ đường thẳng b đi qua A và song song với đường thẳng a cho trước, ta thực hiện theo thứ tự sau:
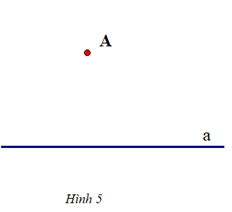
+ Cho đường thẳng a và một điểm A nằm ngoài đường thẳng a
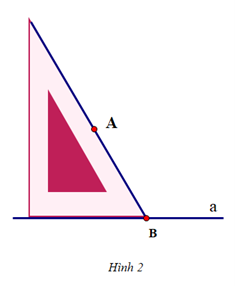
+ Đặt ê ke sao cho cạnh góc vuông ngắn nằm trên đường thẳng a và cạnh huyền đi qua điểm A. Vẽ một đường thẳng theo cạnh huyền của ê ke
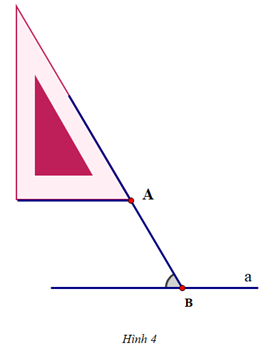
+ Dịch chuyển ê ke sao cho cạnh huyền của ê ke vẫn nằm trên đường thẳng đó còn cạnh góc vuông ngắn của ê ke đi qua điểm A. Vẽ theo cạnh góc vuông ngắn của ê ke một phần đường thẳng b
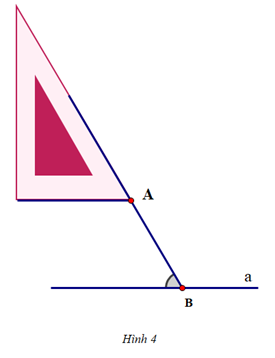
+ Hoàn thiện đường thẳng b
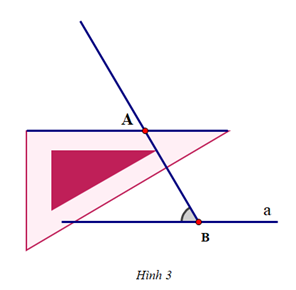
Vậy ta sắp xếp các hình vẽ trên theo thứ tự: Hình 5 – Hình 2 – Hình 4 – Hình 3 – Hình 1====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Để vẽ một đường thẳng d đi qua điểm M và song song với đường thẳng a cho trước, ta thực hiện hai bước như sau:
+ Bước 1: Vẽ đường thẳng c đi qua điểm M và vuông góc với đường thẳng a.
+ Bước 2: Vẽ đường thẳng d đi qua điểm M và vuông góc với đường thẳng c mới vẽ ở bước 1 ta được đường thẳng d song song với đường thẳng a.
Theo em, cách vẽ trên dựa vào tính chất nào sau đây?
Câu hỏi:
Để vẽ một đường thẳng d đi qua điểm M và song song với đường thẳng a cho trước, ta thực hiện hai bước như sau:
+ Bước 1: Vẽ đường thẳng c đi qua điểm M và vuông góc với đường thẳng a.
+ Bước 2: Vẽ đường thẳng d đi qua điểm M và vuông góc với đường thẳng c mới vẽ ở bước 1 ta được đường thẳng d song song với đường thẳng a.
Theo em, cách vẽ trên dựa vào tính chất nào sau đây?A. Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau;
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau;
Đáp án chính xác
C. Hai đường thẳng phân biệt cùng đi qua một điểm thì chúng song song với nhau;
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: B
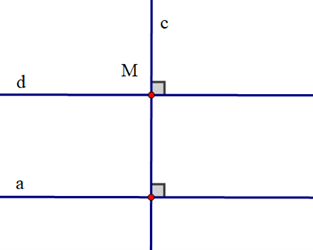
Vì hai đường thẳng a và d cùng vuông góc với đường thẳng c nên chúng song song với nhau. Do đó cách vẽ trên dựa vào tính chất: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đường thẳng a và một điểm M nằm ngoài đường thẳng a:
Khi đó, hình vẽ nào sau đây thể hiện đường thẳng b đi qua M và song song với a?
Câu hỏi:
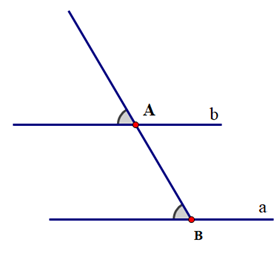
Cho đường thẳng a và một điểm M nằm ngoài đường thẳng a:

Khi đó, hình vẽ nào sau đây thể hiện đường thẳng b đi qua M và song song với a?A.
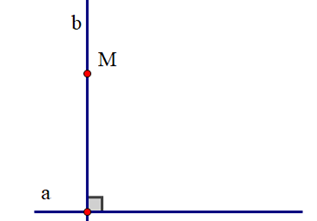 ;
;B.
 ;
;C.
 ;
;Đáp án chính xác
D.
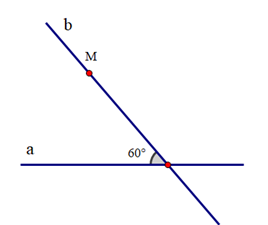 ;
;Trả lời:
Hướng dẫn giải:
Đáp án đúng là: C
Cách vẽ ở hình C cho ta hai đường thẳng a và b song song với nhau vì đường thẳng c cắt hai đường thẳng a và b và tạo thành hai góc ở vị trí so le trong bằng nhau.====== **** mời các bạn xem câu tiếp bên dưới **** =====
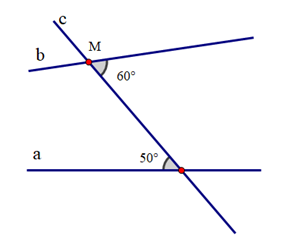
- Vì sao khi sử dụng ê ke (góc 60°) ta có thể vẽ được đường thẳng đi qua một điểm và song song với đường thẳng cho trước?
Câu hỏi:
Vì sao khi sử dụng ê ke (góc 60°) ta có thể vẽ được đường thẳng đi qua một điểm và song song với đường thẳng cho trước?
A. Do hai đường thẳng phân biệt cùng cắt một đường thẳng thứ ba và tạo thành hai góc ở vị trí đồng vị bằng nhau;
Đáp án chính xác
B. Do hai đường thẳng cùng song song với một đường thẳng thứ ba nên chúng song song với nhau;
C. Do hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba nên chúng song song với nhau;
D. Do hai đường thẳng cắt nhau và tạo thành 1 cặp góc trong cùng phía bù nhau.
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: A
Khi vẽ đường thẳng đi qua một điểm và song song với một đường thẳng cho trước, ta có thể sử dụng ê ke (góc 60°) để vẽ vì nó sẽ tạo thành hai góc ở vị trí đồng vị bằng nhau (cùng bằng 60°) nên hai đường thẳng song song với nhau.====== **** mời các bạn xem câu tiếp bên dưới **** =====