Tính các cạnh và các góc chưa biết của tam giác ABC trong Hình 4.

Câu hỏi:

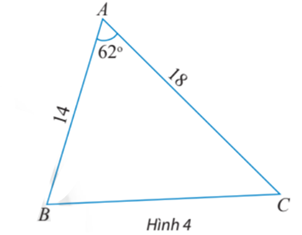
Tính các cạnh và các góc chưa biết của tam giác ABC trong Hình 4.

Trả lời:

Áp dụng định lý côsin cho tam giác ABC ta có:
BC² =  AB² +  AC² – 2AB.AC.cosA   = 14² +  18² – 2.14.18. cos62° ≈ 283,4.
Suy ra BC ≈ 16,8.
Áp dụng hệ quả của định lí côsin ta có:
cosB = $\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC}$  = $\frac{{14}^2+16,8^2-{18}^2}{\mathrm{2.14.16},8}$   ≈ 0,328.
Suy ra  ≈ 71°.
Mặt khác trong tam giác ABC ta có:
$\widehat{A}+\widehat{B}+\widehat{C}={180}^o\Rightarrow \widehat{C}={180}^o-(\widehat{B}+\widehat{C})={180}^o-({71}^o+{62}^o)={47}^o$.
Vậy BC ≈ 16,8;  ≈ 71°; .

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Làm thế nào để tính độ dài cạnh chưa biết của hai tam giác dưới đây?
   
   

   Câu hỏi:
   

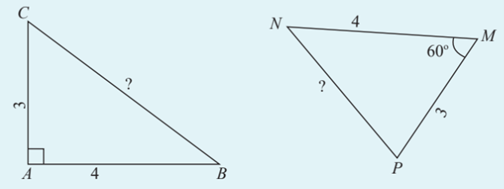
   Làm thế nào để tính độ dài cạnh chưa biết của hai tam giác dưới đây?
   

   Trả lời:

   Quan sát hai tam giác trên, ta thấy tam giác thứ nhất là tam giác vuông nên ta có thể dùng định lí Pythagore để tìm độ dài cạnh chưa biết.
   Ta có tam giác ABC vuông tại A nên BC² = AB² + AC² = 4² + 3² = 25 ⇒ BC = 5.
   Tam giác thứ hai ta chưa biết cách tìm.
   Sau khi học xong bài 2. Định lí côsin và định lí sin ta sẽ giải bài này như sau:
   – Áp dụng định lí côsin cho tam giác ABC ta có:
   BC² = AB² +AC² – 2.AB.AC.cosA = 4² +3² – 2.4.3.cos90° = 25;
   ⇒ BC =  $\sqrt{25}$ = 5.
   Vậy BC = 5.
   – Áp dụng định lí côsin cho tam giác MNP ta có:
   NP² = MN² + MP² – 2.MN.MP.cosM = 4² + 3² – 2.4.3.cos60° = 13;
   ⇒ NP = $\sqrt{13}$  ≈ 3,6.
   Vậy NP ≈ 3,6.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

2. a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và C^≥B^  . Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.   Hãy thay ? bằng chữ cái thích hợp để chứng minh công thức a2 =  b2 +  c2 –  2bccosA theo gợi ý sau: Xét tam giác vuông BCD, ta có: a2 = d2 + (c – x)2 = d2 + x2 + c2 – 2xc. (1) Xét tam giác vuông ACD, ta có: b2 = d2 + x2 ⇒ d2 = b2 – x2                  (2) cosA = ?b  ⇒ ? = bcosA.                                                (3) Thay (2) và (3) vào (1), ta có: a2 =  b2 +  c2 – 2bccosA. Lưu ý : Nếu B^>C^  thì ta vẽ đường cao BD và chứng minh tương tự. b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có: a2 =  b2 +  c2  – 2bccosA. Lưu ý: Vì A tù nên cosA = −xb. c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ công thức a2 =  b2 +  c2 – 2bccosA có thể viết là a2 =  b2 +  c2.
   
   

   Câu hỏi:
   

   a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và $\widehat{C}\ge \widehat{B}$  . Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.
   
    

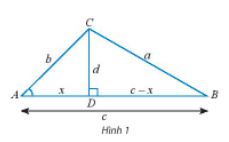
   Hãy thay ? bằng chữ cái thích hợp để chứng minh công thức a² =  b² +  c² –  2bccosA theo gợi ý sau:
   Xét tam giác vuông BCD, ta có: a² = d² + (c – x)² = d² + x² + c² – 2xc. (1)
   Xét tam giác vuông ACD, ta có: b² = d² + x² ⇒ d² = b² – x²                  (2)
   cosA = $\frac{?}{b}$  ⇒ ? = bcosA.                                                (3)
   Thay (2) và (3) vào (1), ta có: a² =  b² +  c² – 2bccosA.
   Lưu ý : Nếu $\widehat{B}>\widehat{C}$  thì ta vẽ đường cao BD và chứng minh tương tự.
   b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:
   a² =  b² +  c²  – 2bccosA.
   Lưu ý: Vì A tù nên cosA = $-\frac{x}{b}$.
   

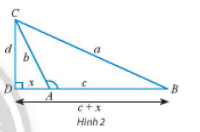
   c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ công thức a² =  b² +  c² – 2bccosA có thể viết là a² =  b² +  c².

   Trả lời:

   a)
   

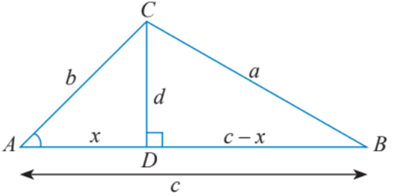
   Xét tam giác vuông ACD, ta có: cosA = $\frac{AD}{AC}=\frac{x}{b}$  ⇒ x = bcosA.
   Vậy lời giải đúng:
   Xét tam giác vuông BCD, ta có: a² = d² + (c – x)² = d² + x² + c² – 2xc. (1)
   Xét tam giác vuông ACD, ta có: b² = d² + x² ⇒ d² = b² –  x²                 (2)
   cosA = $\frac{x}{b}$  ⇒ x = bcosA.                                            (3)
   Thay (2) và (3) vào (1), ta có : a² =  b² +  c² –  2bccosA.
   b) Với tam giác ABC có góc A tù :
   

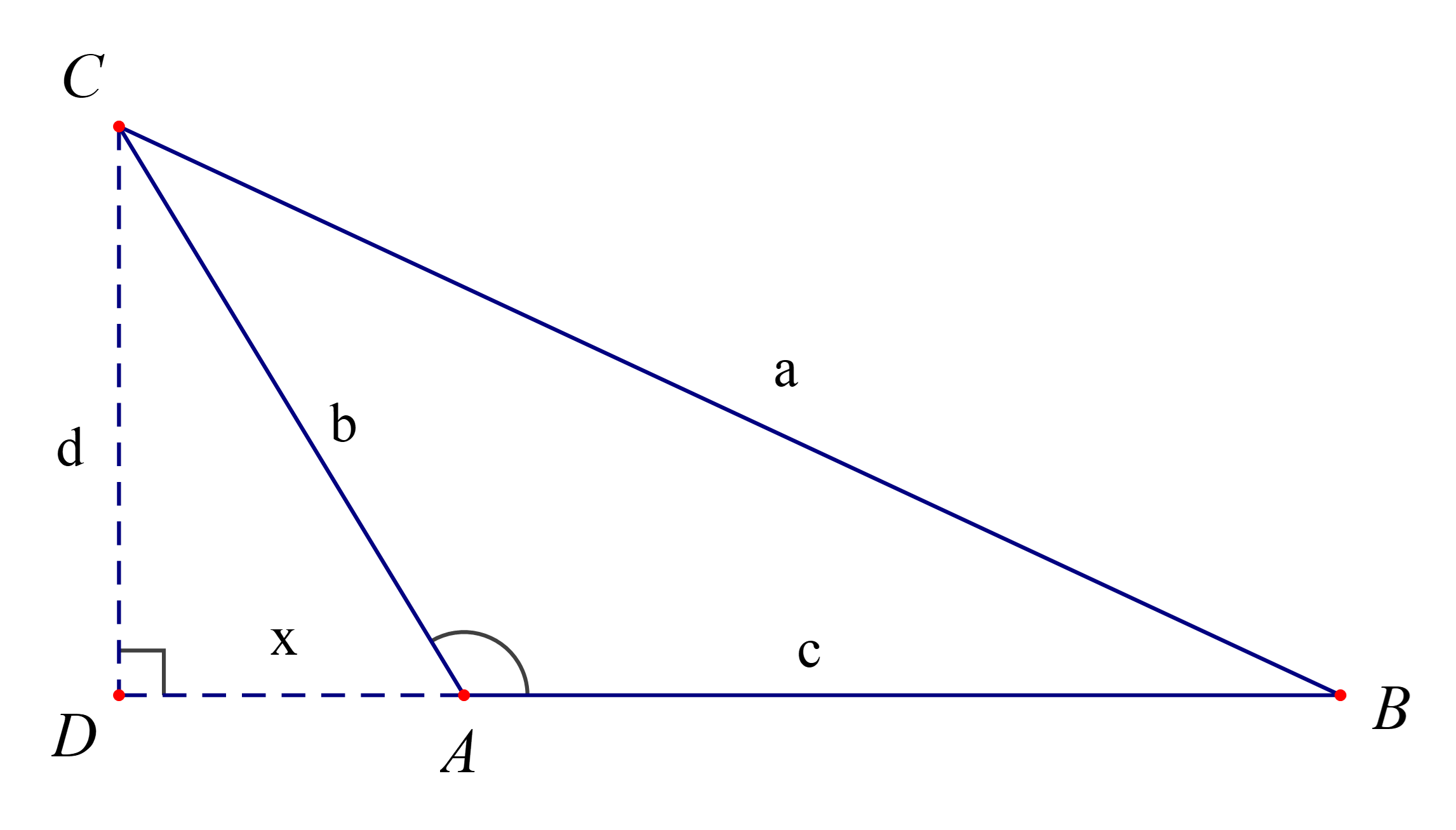
   Xét tam giác vuông BCD, ta có: a² = d² + (x + c)² = d² + x² + c² + 2xc. (4)
   Xét tam giác vuông ACD, ta có: b² = d² + x² ⇒ d² = b² –  x²          (5)
   cos $\widehat{CAD}$ = $\frac{AD}{AC}=\frac{x}{b}$  .
   Do  $\widehat{CAD}+\widehat{CAB}={180}^o\Rightarrow \widehat{CAB}={180}^o-\widehat{CAD}$  .
   Suy ra: cos $\widehat{CAB}$ = cos $({180}^o-\widehat{CAD})$ = – cos $\widehat{CAD}$ =   $-\frac{x}{b}$ 
   ⇒ cos $\widehat{CAB}$ =    $-\frac{x}{b}$
   ⇒ x = –bcos$\widehat{CAB}$ , tức là x = – bcosA                        (6)
   Thay (5) và (6) vào (4), ta được : a² =  b² +  c^{2 _} 2bccosA.
   Vậy với tam giác ABC có góc A tù ta cũng có : a² =  b² +  c²  – 2bccosA.
   c) Với tam giác ABC vuông tại A thì cosA = cos90° = 0.
   Suy ra a² =  b² +  c² – 2bccosA = b² +  c² – 2bc.0 = b² +  c².
   Vậy a² =  b² +  c².

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

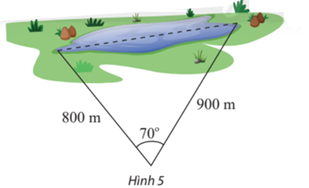
3. Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 800 m và 900 m người quan sát nhìn hai điểm này dưới một góc 70° (Hình 5).
   
   

   Câu hỏi:
   

   Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 800 m và 900 m người quan sát nhìn hai điểm này dưới một góc 70° (Hình 5).
   

   Trả lời:

   

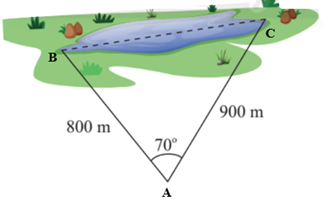
   Gọi A là điểm người đứng quan sát, B và C lần lượt là hai đầu của hồ nước.
   Khi đó AB = 800 m; AC = 900 m; $\widehat{A}={70}^o$  .
   Tính khoảng cách giữa hai đầu hồ nước chính là tính độ dài cạnh BC của tam giác ABC.
   Áp dụng định lý côsin cho tam giác ABC ta có:
   BC² =  AB² +  AC² – 2AB.AC.cosA   = 800² +  900² – 2.800.900. cos70° ≈ 957 491
   Suy ra BC ≈ 978,5 (m).
   Vậy khoảng cách giữa hai đầu hồ nước khoảng 978,5 m.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

4. a) Cho tam giác ABC không phải là tam giác vuông có BC = a, AC = b; AB = c và R là bán kính đường tròn ngoại tiếp tam giác đó. Vẽ đường kính BD. i) Tính sin BDC^ theo a và R. ii) Tìm mối liên hệ giữa hai góc BAC^ và BDC^ . Từ đó chứng minh rằng 2R = asinA . b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức 2R = asinA .
   
   

   Câu hỏi:
   

   a) Cho tam giác ABC không phải là tam giác vuông có BC = a, AC = b; AB = c và R là bán kính đường tròn ngoại tiếp tam giác đó. Vẽ đường kính BD.
   i) Tính sin $\widehat{BDC}$ theo a và R.
   ii) Tìm mối liên hệ giữa hai góc $\widehat{BAC}$ và $\widehat{BDC}$ . Từ đó chứng minh rằng 2R = $\frac{a}{\sin A}$ .
   

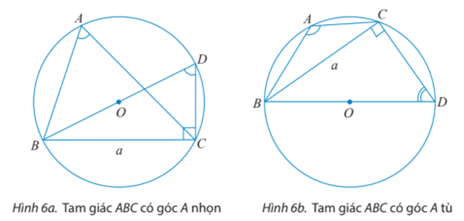
   b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức 2R = $\frac{a}{\sin A}$ .

   Trả lời:

   a)
   i) Do BD là đường kính của đường tròn nên tam giác BCD vuông tại C.
   ⇒ sin $\widehat{BDC}$  = $\frac{BC}{BD}=\frac{a}{2R}$
   Vậy sin $\widehat{BDC}$  = $\frac{a}{2R}$ .
   ii)
   +) Trường hợp tam giác ABC có góc A nhọn:
   Hai góc $\widehat{BAC}$  và $\widehat{BDC}$  là hai góc nội tiếp cùng chắn , do đó  $\widehat{BAC}$= $\widehat{BDC}$ .
   Suy ra sin $\widehat{BAC}$ = sin$\widehat{BDC}$  =  $\frac{a}{2R}$
   ⇒ 2R = $\frac{a}{\sin \widehat{BAC}}$  , tức là 2R = $\frac{a}{\sin A}$  .
   Vậy 2R = $\frac{a}{\sin A}$ .
   +) Trường hợp tam giác ABC có góc A tù:
   Tứ giác ABDC nội tiếp đường tròn tâm O nên ta có $\widehat{BAC}$  + $\widehat{BDC}$  =180°;
   ⇒  $\widehat{BDC}$ = 180° – $\widehat{BAC}$  ;
   ⇒ sin $\widehat{BDC}$= sin(180^o – $\widehat{BAC}$ )= sin $\widehat{BAC}$;
   ⇒ sin $\widehat{BAC}$ = sin  $\widehat{BDC}$=  $\frac{a}{2R}$
   ⇒ 2R = $\frac{a}{\sin \widehat{BAC}}$  , tức là 2R = $\frac{a}{\sin A}$ .
   Vậy 2R = $\frac{a}{\sin A}$  .
   b) Với tam giác ABC vuông tại A. Khi đó BC sẽ là đường kính của đường tròn ngoại tiếp tam giác ABC nên BC = 2R.
   

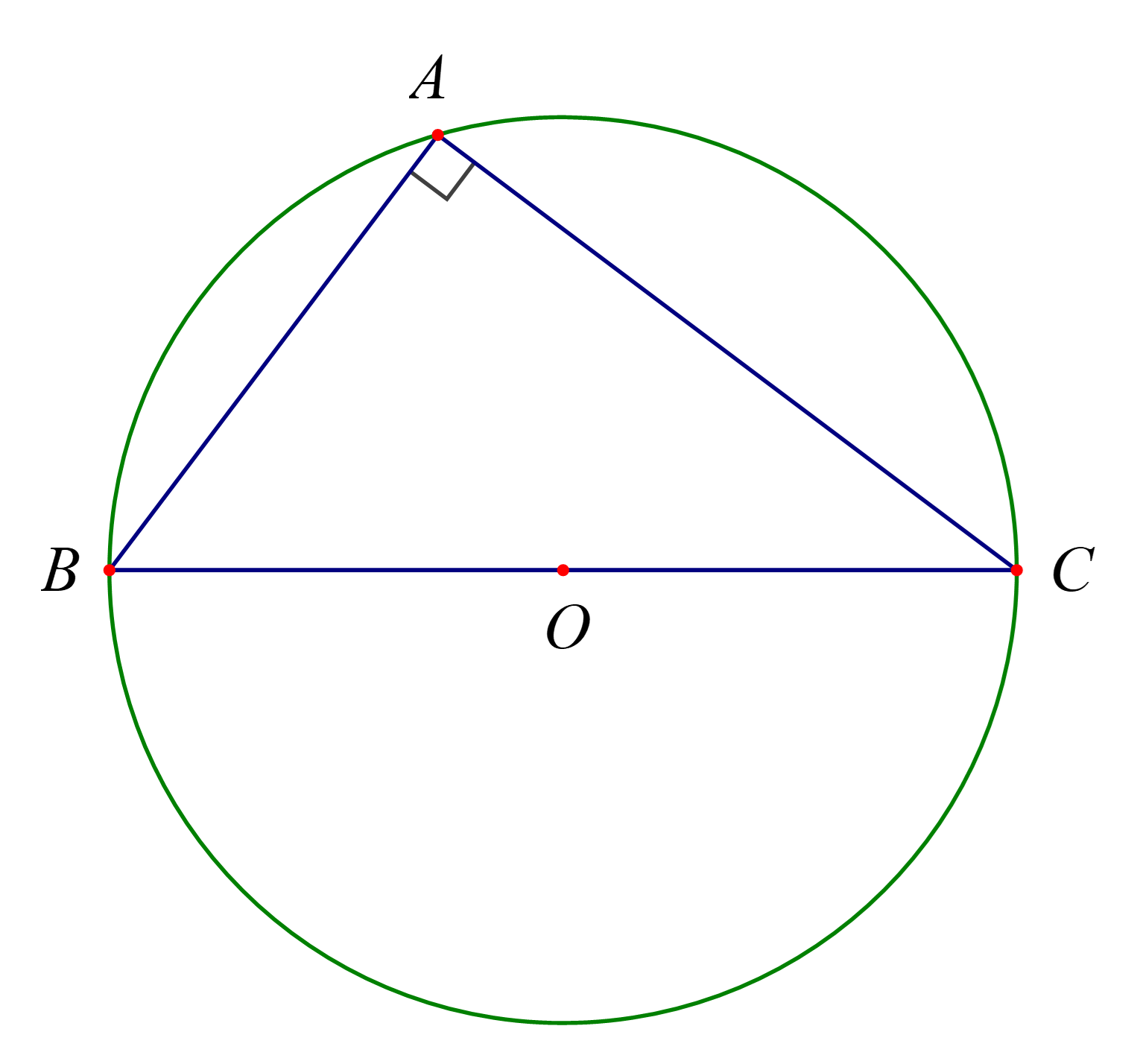
   ⇒ sinA = sin90°  = 1 và $\frac{a}{\sin A}=\frac{BC}{1}=BC=2R$ .
   Vậy tam giác ABC vuông tại A thì ta vẫn có công thức 2R = $\frac{a}{\sin A}$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

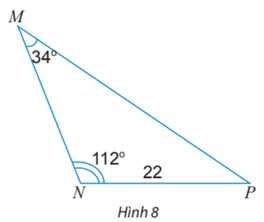
5. Tính các cạnh và các góc chưa biết của tam giác MNP trong Hình 8.
   
   

   Câu hỏi:
   

   Tính các cạnh và các góc chưa biết của tam giác MNP trong Hình 8.
   

   Trả lời:

   Trong tam giác MNP ta có :
   $\widehat{M}+\widehat{N}+\widehat{P}={180}^o\Rightarrow \widehat{P}={180}^o-(\widehat{M}+\widehat{N})={180}^o-({34}^o+{112}^o)={34}^o$.
   Suy ra $\widehat{M}=\widehat{P}={34}^o$  nên tam giác MNP cân tại N.
   Do đó MN = NP = 22.
   Áp dụng định lí sin cho tam giác MNP ta có : $\frac{MP}{\sin N}=\frac{NP}{\sin M}=\frac{MN}{\sin P}$ .
   Suy ra $\frac{MP}{\sin {112}^o}=\frac{22}{\sin {34}^o}\Rightarrow MP=\frac{22.\sin {112}^o}{\sin {34}^o}\approx 36,5$ .
   Vậy các cạnh và các góc chưa biết của tam giác MNP là : $\widehat{P}={34}^o$  ; MN = 22 ; MP ≈ 36,5.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====