Cho hình chóp S.ABC có M là điểm di động trên cạnh SA sao cho SMSA=kk∈ℝ,0

Câu hỏi:

Cho hình chóp S.ABC có M là điểm di động trên cạnh SA sao cho $\frac{SM}{SA}=k\left(k\in ℝ,0<k<1\right).$ Gọi $\left(\alpha \right)$ là mặt phẳng đi qua M và song song với mặt phẳng $\left(ABC\right)$. Tìm k để mặt phẳng $\left(\alpha \right)$ cắt hình chóp S.ABC theo một thiết diện có diện tích bằng một nửa diện tích tam giác ABC.

A. $k=\frac{\sqrt{2}}{2}.$

Đáp án chính xác

B. $k=\frac{1}{3}.$

C. $k=\frac{\sqrt{3}}{2}.$

D. $k=\frac{1}{2}.$

Trả lời:

Đáp án A

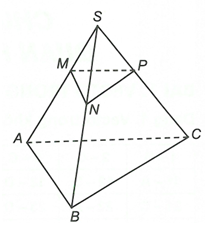
Gọi N, P là hai điểm lần lượt thuộc SB, SC thỏa mãn $MN\text{ // }AB, MP\text{ // }AC.$
Ta có $\left\{\begin{array}{l}MN\text{ // }AB\Rightarrow MN\text{ // }\left(ABC\right)\\ MP\text{ // }AC\Rightarrow MP\text{ // }\left(ABC\right)\end{array}\right.\Rightarrow \left(MNP\right)\text{ // }\left(ABC\right).$
Gọi $h_1$ là đường cao của $\Delta MNP$ ứng với đáy MN.
Gọi $h_2$ là đường cao của $\Delta ABC$ ứng với đáy AB.
Dễ thấy $\Delta MNP$ đồng dạng $\Delta ABC$ ta có $\frac{MN}{AB}=\frac{h_1}{h_2}=k.$
Vậy để thỏa mãn yêu cầu bài toán
$\frac{S_{\Delta MNP}}{S_{\Delta ABC}}=\frac{\frac{1}{2}{h}_1.MN}{\frac{1}{2}{h}_2.AB}=\frac{1}{2}\iff k.k=\frac{1}{2}\iff k=\frac{\sqrt{2}}{2}.$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Tam giác SBD đều. Một mặt phẳng (P) song song với (SBD) và đi qua điểm I thuộc cạnh AC (không trùng với A hoặc C). Tìm thiết diện của (P) và hình chóp.
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Tam giác SBD đều. Một mặt phẳng (P) song song với (SBD) và đi qua điểm I thuộc cạnh AC (không trùng với A hoặc C). Tìm thiết diện của (P) và hình chóp.

   Trả lời:

   
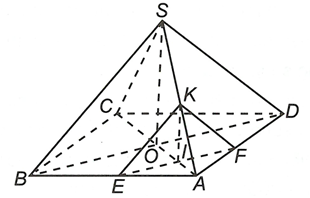
   Gọi $\left\{O\right\}=AC\cap DB.$
   Do SO nằm trong $\left(SBD\right)$ nên $SO\text{ // }\left(\alpha \right).$
   Mặt phẳng (SAC) chứa SO và có điểm chung với $\left(\alpha \right)$ là I, do đó $\left(SAC\right)\cap \left(\alpha \right)=IK$ với $IK\text{ // }SO$ và $K\in SA.$
   Tương tự $\left(SAB\right)\cap \left(\alpha \right)=KE$ với $KE\text{ // }SB$ và $E\in AB.$
   $\left(SAD\right)\cap \left(\alpha \right)=KF$ với $KF\text{ // }SD$ và $F\in AD.$
   Suy ra thiết diện của (P) với hình chóp S.ABCD là tam giác KEF.
   Ta có $\frac{EF}{BD}=\frac{AE}{AB}=\frac{AF}{AD}=\frac{AK}{AS}=\frac{KE}{SB}=\frac{KF}{SD}$
   $\Rightarrow \Delta SBD$ đồng dạng với $\Delta KEF.$
   Tam giác SBD là tam giác đều nên $\Delta KEF$ cũng là tam giác đều.
   Vậy thiết diện của (P) và hình chóp S.ABCD là tam giác đều.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

2. Cho hình lăng trụ ABC.A’B’C’. Gọi I, J, K lần lượt là trọng tâm tam giác ABC, ACC’, AB’C’. Chứng minh (IJK) // (BB’C)
   
   

   Câu hỏi:
   

   Cho hình lăng trụ ABC.A’B’C’. Gọi I, J, K lần lượt là trọng tâm tam giác ABC, ACC’, AB’C’. Chứng minh (IJK) // (BB’C)

   Trả lời:

   
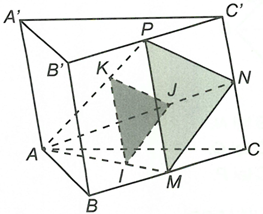
   Gọi M, N, P lần lượt là trung điểm $BC;C{C}^{‘};B^{‘}{C}^{‘}.$
   Do I, J, K lần lượt là trọng tâm tam giác $ABC,AC{C}^{‘}$ nên $\frac{AI}{AM}=\frac{AJ}{AN}=\frac{2}{3}$ nên $IJ\text{ // }MN\Rightarrow IJ\text{ // }\left(BC{C}^{‘}{B}^{‘}\right).$
   Tương tự $IK\text{ // }\left(BC{C}^{‘}{B}^{‘}\right)\Rightarrow \left(IJK\right)\text{ // }\left(BC{C}^{‘}{B}^{‘}\right).$
   Hay $\left(IJK\right)\text{ // }\left(B{B}^{‘}C\right).$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

3. Cho hình chóp cụt tam giác ABC.A'B'C' có hai đáy là hai tam giác vuông tại A và A' và có ABA'B'=12. Khi đó tỉ số diện tích SΔABCSΔA'B'C' bằng bao nhiêu?
   
   

   Câu hỏi:
   

   Cho hình chóp cụt tam giác ABC.A’B’C’ có hai đáy là hai tam giác vuông tại A và A’ và có $\frac{\mathrm{AB}}{{\mathrm{A}}^{‘}{\mathrm{B}}^{‘}}=\frac{1}{2}.$ Khi đó tỉ số diện tích $\frac{{\mathrm{S}}_{\mathrm{\Delta ABC}}}{{\mathrm{S}}_{{\mathrm{\Delta A}}^{‘}{\mathrm{B}}^{‘}{\mathrm{C}}^{‘}}}$ bằng bao nhiêu?

   Trả lời:

   
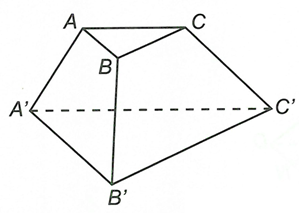
   Hai tam giác ABC và A’B’C’ đồng dạng  $\frac{AB}{A^{‘}{B}^{‘}}=\frac{BC}{B^{‘}{C}^{‘}}=\frac{CA}{C^{‘}{A}^{‘}}=\frac{1}{2}$ nên $\frac{S_{\Delta ABC}}{S_{\Delta A^{‘}{B}^{‘}{C}^{‘}}}=\frac{\frac{1}{2}AB.AC.\sin A}{\frac{1}{2}{A}^{‘}{B}^{‘}.A^{‘}{C}^{‘}.\sin A^{‘}}=\frac{1}{4}.$
   Cách khác: Tỉ số diện tích hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng nên $\frac{S_{\Delta ABC}}{S_{\Delta A^{‘}{B}^{‘}{C}^{‘}}}={\left(\frac{1}{2}\right)}^2=\frac{1}{4}.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

4. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 10. Gọi M là điểm trên SA sao cho SMSA=23. Một mặt phẳng α đi qua M song song với AB và CD, cắt hình chóp theo một tứ giác. Tính diện tích tứ giác đó.
   
   

   Câu hỏi:
   

   Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 10. Gọi M là điểm trên SA sao cho $\frac{SM}{SA}=\frac{2}{3}.$ Một mặt phẳng $\left(\alpha \right)$ đi qua M song song với AB và CD, cắt hình chóp theo một tứ giác. Tính diện tích tứ giác đó.

   Trả lời:

   
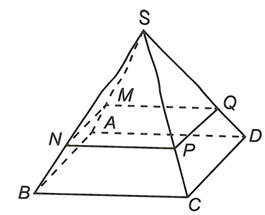
   Qua M dựng đường thẳng song song AB cắt SB tại N.
   Qua M dựng đường thẳng song song AD cắt SD tại Q.
   Qua N dựng đường thẳng song song BC cắt SC tại P.
   Ta có $\left\{\begin{array}{l}MN\text{ // }AB\Rightarrow MN\text{ // }\left(ABCD\right)\\ NP\text{ // }BC\Rightarrow NP\text{ // }\left(ABCD\right)\end{array}\right.\Rightarrow \left(MNPQ\right)\text{ // }\left(ABCD\right).$
   Ta có tỉ lệ diện tích $\frac{S_{MNPQ}}{S_{ABCD}}={\left(\frac{MN}{AB}\right)}^2={\left(\frac{SM}{SA}\right)}^2=\frac{4}{9}.$
   Lại có $S_{ABCD}=10.10=100\iff S_{MNPQ}=100.\frac{4}{9}=\frac{400}{9}.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

5. Cho hình chóp S.ABCD với ABCD là hình thoi cạnh a, SAD là tam giác đều. Gọi M là một điểm thuộc cạnh AB, AM = x, (P) là mặt phẳng qua M song song với (SAD). Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P).
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD với ABCD là hình thoi cạnh a, SAD là tam giác đều. Gọi M là một điểm thuộc cạnh AB, AM = x, (P) là mặt phẳng qua M song song với (SAD). Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P).

   Trả lời:

   
   Do $\left(P\right)$ đi qua M và song song với $\left(SAD\right)$ nên cắt các mặt của hình chóp bằng các giao tuyến đi qua M và song song với $\left(SAD\right)$. Do ABCD là hình thoi và tam giác SAD đều. Nên thiết diện thu được là hình thang cân MNEF $\left(MN\text{ // }EF;MF=EN\right).$
   Ta có $MN=a,\frac{EF}{BC}=\frac{SF}{SB}=\frac{MA}{AB}=\frac{x}{a}\Rightarrow EF=x;MF=a-x.$
   Đường cao FH của hình thang cân bằng $FH=\sqrt{M{F}^2-{\left(\frac{MN-EF}{2}\right)}^2}=\frac{\sqrt{3}}{2}\left(a-x\right).$
   Khi đó diện tích hình thang cân là $S=\frac{\sqrt{3}}{4}\left(a^2-x^2\right)$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====