Bài 1 trang 102 sách bài tập Toán lớp 6 Tập 2: Hãy nối mỗi hình ảnh ở cột bên trái với tên một hình hình học phù hợp.

By admin 06/06/2023 0

Câu hỏi:

Hình ảnh thực tiễn

Hình hình học

(1)
Hãy nối mỗi hình ảnh ở cột bên trái với tên một hình hình học phù hợp

(A) Điểm

(2)
Hãy nối mỗi hình ảnh ở cột bên trái với tên một hình hình học phù hợp

(B) Tia

(3)
Hãy nối mỗi hình ảnh ở cột bên trái với tên một hình hình học phù hợp

(4)
Hãy nối mỗi hình ảnh ở cột bên trái với tên một hình hình học phù hợp

(D) Đoạn thẳng

Trả lời:

Lời giải:
Hình ảnh (1) là những ngôi sao trên bầu trời đêm, khi nhìn xa ta chỉ thấy các điểm sáng. Do đó, (1) nối với (A).
Hình ảnh (2) là một người đang nâng tạ, quả tạ thể hiện như đoạn thẳng (bị giới hạn hai đầu). Do đó, (2) nối với (D).
Hình ảnh (3) là một hai chùm tia sáng, chùm sáng có đặc điểm xuất phát từ một điểm (nguồn sáng) và chiếu loe rộng ra nhiều phía thể hiện như tia. Do đó, (3) nối với (B).
Hình ảnh (4) là đường ống dẫn nước, kéo dài qua rất nhiều nơi (có thể coi như nó không bị giới hạn hai đầu) nên ống nước thể hiện như đường thẳng. Do đó, (4) nối với (C).
Vậy ta nối được như sau:
(1) – (A);
(2) – (D);
(3) – (B);
(4) – (C).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

30 câu Trắc nghiệm Chương 8: Tam giác (Chân trời sáng tạo) có đáp án 2023 – Toán lớp 7

Trắc nghiệm Toán 7 Chương 8: Tam giác

Câu 1. Cho tam giác ABC có E, F lần lượt là trung điểm của AB và BC. Cho O cách

đều ba đỉnh của tam giác ABC. Khi đó:

A. OE vuông góc với AC;

B. OE vuông góc với AB;

C. OF vuông góc với AC;

D. OF vuông góc với AB.

Hướng dẫn giải

Đáp án đúng là: B

Xét ∆ABC có điểm O cách đều ba đỉnh của tam giác ABC.

Do đó O là giao điểm của ba đường trung trực của ∆ABC.

Mà E là trung điểm của AB.

Nên OE là đường trung trực của AB.

Vậy OE vuông góc với AB tại E.

Câu 2. Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số $\frac{A G}{A M}$ bằng:

A. 2

B. $\frac{1}{3}$

C. $\frac{3}{4}$

D. $\frac{1}{2}$

Hướng dẫn giải

Đáp án đúng là: A

Xét ∆ABC có:

AM là đường trung tuyến (M là trung điểm của BC);

BN là đường trung tuyến (N là trung điểm của AC).

AM và BN cắt nhau tại G.

Do đó G là trọng tâm của ∆ABC.

Suy ra $\frac{A G}{A M}$ = $\frac{2}{3}$ và $\frac{G M}{A M}$ = $\frac{1}{3}$ .

Ta có: $\frac{A G}{A M}$ : $\frac{G M}{A M}$ = $\frac{A G}{A M}$ = $\frac{2}{3}$ : $\frac{1}{3}$ = 2.

Vậy $\frac{A G}{A M}$ = 2.

Câu 3. Cho tam giác ∆ABC cân tại A có hai đường trung tuyến BH và CK cắt nhau tại G. Biết BG = 6 cm. Độ dài đoạn thẳng CK bằng:

A. 9 cm;

B. 10 cm;

C. 12 cm;

D. 8 cm.

Hướng dẫn giải

Đáp án đúng là: A

Ta có: ∆ABC cân tại A.

Suy ra AB = AC mà AB = 2AK; AC = 2AH.

Do đó 2AK = 2AH hay AK = AH.

Xét ∆ABH và ∆ACK có:

$\hat{A}$ là góc chung;

AB = AC (∆ABC cân tại A);

AK = AH (cmt).

Do đó ∆ABH = ∆ACK (c.g.c).

Suy ra CK = BH (hai cạnh tương ứng).

Mà CK = $\frac{3}{2}$ CG ; BH = $\frac{3}{2}$ BG (G là trọng tâm của ∆ABC).

Nên $\frac{3}{2}$ CG = $\frac{3}{2}$ BG hay CG = BG = 6 (cm).

Do vậy BH = $\frac{3}{2}$ . 6 = 9 (cm).

Vậy độ dài đoạn thẳng BH bằng 9 cm.

Câu 4. Cho tam giác ABC có hai đường trung tuyến AD và CE cắt nhau tại G. Đường thẳng BG cắt AC tại F. Cho AC = 10 cm. Độ dài đoạn thẳng AF bằng:

A. 10 cm;

B. 4 cm;

C. 5 cm;

D. 8 cm.

Hướng dẫn giải

Đáp án đúng là: C

Xét ∆ABC có:

AD là đường trung tuyến (gt);

BE là đường trung tuyến (gt).

AD và BE cắt nhau tại G.

Do đó G là giao điểm của ba đường trung tuyến của tam giác ABC.

Suy ra BG là đường trung tuyến của ∆ABC.

Nên F là trung điểm của AC.

Ta có: AF = $\frac{A C}{2} = \frac{10}{2}$ = 5 (cm)

Vậy độ dài đoạn thẳng AF bằng 5 cm.

Câu 5. Cho tam giác DEF vuông tại E. Trên tia DE lấy điểm M sao sao DM = DF. Tia phân giác của góc $\hat{D}$ cắt EF tại H . Khi đó:

A. MH vuông góc với EF;

B. MH vuông góc với DF;

C. H là trực tâm của ∆MDF;

D. B và C đều đúng.

Hướng dẫn giải

Đáp án đúng là: D

Gọi I là giao điểm của DH và MF.

G là giao điểm của MH và DF.

Xét ∆DMI và ∆DFI ta có:

MD = MF (gt);

$\hat{M D I} = \hat{I D F}$ (DI là tia phân giác góc MDF);

DI là cạnh chung.

Do đó ∆DMI = ∆DFI (c.g.c).

Suy ra $\hat{M I D} = \hat{D I F}$ ( hai góc tương ứng) .

Do đó $\hat{M I D} = \hat{D I F}$ = $\frac{180 °}{2}$ = 90°.

Vậy DI vuông góc với MF tại I.

Xẻt ∆DMF có:

FE là đường cao (FE vuông góc với MD tại E);

DI là đường cao (DI vuông góc với MF tại I);

FE và DI cắt nhau tại H.

Do đó H là trực tâm và là giao điểm của ba đường cao trong ∆DMF.

Suy ra MH là đường cao của ∆DMF hay MH vuông góc với DF tại G.

Vậy cả hai đáp án B và C đều đúng.

Câu 6. Cho hình vẽ như bên dưới. Khi đó:

A. AE là đường trung trực của BC;

B. D là trung điểm của AE;

C. D cách đều hai điểm A và E;

D. Tất cả đáp án trên đều sai

Hướng dẫn giải

Đáp án đúng là: A

Ta có: A cách đều hai điểm B và C (AB = AC).

E cách đều hai điểm B và C (EB = EC).

Do đó AE là đường trung trực của BC (tính chất của đường trung trực).

Câu 7. Cho tam giác ABC nhọn có đường trung trực AD với D nằm trên BC. Khi đó:

A. AD là tia phân giác góc $\hat{B A C}$ ;

B. ∆ABC vuông cân tại A;

C. ∆ABC cân tại A;

D. A và B đều đúng.

Hướng dẫn giải

Đáp án đúng là: D

Xét ∆ABD và ∆ACD cùng vuông tại D có:

AD là cạnh chung;

BD = DC (D là trung điểm của BC).

Do đó ∆ABD = ∆ACD (hai cạnh góc vuông)

Suy ra AB = AC (hai cạnh tương ứng).

Do đó tam giác ABC cân tại A.

Ta có: $\hat{B A D} = \hat{D A C}$ (∆ABD = ∆ACD).

Do đó AD là tia phân giác góc $\hat{B A C}$ .

Do vậy cả 2 đáp án A và B đều đúng.

Câu 8. Cho hai điểm D và E nằm trên đường trung trực của đoạn thẳng AB. Cho $\hat{D A E}$ = 20°. Số đo $\hat{D B E}$ bằng :

A. 20°;

B. 30°;

C. 40°;

D. 10°.

Hướng dẫn giải

Đáp án đúng là: A

Vì D nằm trên đường trung trực của AB nên DA = DB (tính chất của đường trung trực).

Vì E nằm trên đường trung trực của AB nên EA = EB (tính chất của đường trung trực).

Xét ∆DEA và ∆DEB có:

DA = DB (cmt);

EA = EB (cmt);

DE là cạnh chung.

Do đó ∆DEA = ∆DEB (c.c.c)

Suy ra $\hat{D A E} = \hat{D B E}$ = 20°.

Vậy $\hat{D B E}$ = 20°.

Câu 9. Cho ∆ABC có E và D lần lượt là trung điểm của AB và BC. Từ E và D kẻ đường trung trực cắt nhau tại O. Cho F là trung điểm của AC. Khi đó:

A.OF là đường trung tuyến;

B. OF là đường trung trực của AC;

C. O là trực tâm của ∆ABC;

D. B và C đều đúng.

Hướng dẫn giải

Đáp án đúng là: D

Xét ∆ABC có:

OE là đường trung trực của AB (gt);

OD là đường trung trực của BC (gt);

OE và OD cắt nhau tại O.

Do đó O là trực tâm của ∆ABC.

Mà F là trung điểm của AC.

Nên OF là đường trung trực của AC.

Vậy đáp án B và C đều đúng.

Câu 10. Trong khu dân cư có ba điểm dân cư D, E, F người ta muốn xây một công viên H cách đều cả ba điểm dân cư (như hình vẽ).

Khi đó vị trí của H là:

A. Trung điểm của EF;

B.Trọng tâm của ∆DEF;

C. Giao của ba đường trung trực của ∆DEF;

D.A và C đều đúng.

Hướng dẫn giải

Đáp án đúng là: C

Gọi ba điểm dân cư D, E, F là ba đỉnh của ∆DEF

Để công viên H cách đều ba điểm dân cư thì H phải cách đều ba đỉnh của ∆DEF.

Do đó H là giao điểm của ba đường trung trực trong ∆DEF.

Câu 11. Cho tam giác ABC có đường cao BE và trực tâm K. Gọi H là giao điểm của AK và BC. Từ C kẻ đường thẳng vuông góc với BC cắt AB tại D. Khẳng định nào sau đây là đúng?

A. CD // AH;

B. CD // AB;

C.CD // BE;

D. CD $⊥$ BE;

Hướng dẫn giải

Đáp án đúng là: A

Xét ∆ABC có:

K là trực tâm (gt);

AK cắt BC tại H(gt).

Do đó AH là đường cao của ∆ABC.

Suy ra AH $⊥$ BC tại H.

Mà CD $⊥$ BC tại C.

Nên CD // AH.

Câu 12. Cho hình vẽ như bên dưới.Biết AH = 6 cm, BC = 8cm.

Diện tích tam giác ABC bằng:

A. 28 cm²;

B. 26 cm²;

C. 34 cm²;

D. 30 cm².

Hướng dẫn giải

Đáp án đúng là: D

Xét ∆ABC cân tại A có AH là đường trung tuyến (H là trung điểm của BC).

Do đó AH cũng là đường cao của ∆ABC.

S_ABC $\frac{A H . B C}{2}$ = $\frac{6.8}{2}$ = $\frac{48}{2}$ = 24 (cm²).

Vậy diện tích tam giác ABC bằng 24 cm².

Câu 13. Cho ∆ABC cân tại A có hai đường phân giác từ góc Bvà góc C cắt nhau tại G. Cho góc $\hat{B A C}$ = 40°. Số đo $\hat{B G C}$ bằng:

A. 60°;

B. 90°;

C. 110°;

D. 120°.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: $\hat{A B C}$ = $\hat{A C B}$ ( ∆ABC cân tại A);

$\hat{A B C} + \hat{A C B} + \hat{B A C}$ = 180° (tổng ba góc trong tam giác).

Do đó $\hat{A B C}$ = $\hat{A C B}$ = $\frac{180 ° - \hat{B A C}}{2}$ = $\frac{180 ° - 40 °}{2}$ = $\frac{140 °}{2}$ = 70°.

Ta có: $\hat{A B C}$ = $\hat{A C B}$ .

$\hat{G B C}$ = $\frac{1}{2}$ $\hat{A B C}$ (BG là tia phân giác góc ).

$\hat{G C B}$ = $\frac{1}{2}$ $\hat{A C B}$ ( CG là tia phân giác góc ).

Do đó $\hat{G B C}$ = $\hat{G C B}$ = $\frac{1}{2}$ $\hat{A B C}$ = $\frac{1}{2}$ . 70° = 45°.

Ta có : $\hat{G B C}$ + $\hat{G C B}$ + $\hat{B G C}$ = 180° (tổng ba góc trong tam giác).

$\hat{G B C}$ = $\hat{G C B}$ = 45° (cmt).

Do đó $\hat{B G C}$ = 180°−45°−45° = 90°.

Vậy $\hat{B G C}$ = 90°.

Câu 14. Cho ∆ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Khẳng định nào sau đây là đúng?

A. Ba điểm A, G, I thẳng hàng;

B. Điểm G nằm trên đường phân giác của góc B;

C. Điểm G cách đều ba đỉnh của ∆ABC;

D.Điểm G cách đều ba cạnh của ∆ABC.

Hướng dẫn giải

Đáp án đúng là: A

Gọi M là giao điểm của AI và BC.

Do I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác ABC nên I thuộc các đường phân giác của tam giác ABC.

Do đó I thuộc đường phân giác AM của $\hat{B A C}$ .

Mà ∆ABC cân tại A nên đường phân giác AM cũng là đường trung tuyến của ∆ABC.

Suy ra I thuộc đường thẳng AM.

Do G cũng thuộc AM (G là trọng tâm ∆ABC).

Do đó ba điểm A, G,I thẳng hàng.

Câu 15. Một hòn đảo bị chia cắt bởi đường bờ biển tạo thành một hình tam giác. Các đường bờ biển được kí hiệu là các đường m,n,p(như hình vẽ). Người ta đặt một ngọn hải đăng trên hòn đảo để quan sát xung quanh. Vị trí của hải đăng để khoảng cách từ đó đến 3 đường bờ biển bằng nhau là:

A. Giao điểm ba đường trung tuyến của tam giác;

B. Giao điểm ba đường trung trực của tam giác;

C. Giao điểm ba đường cao của tam giác;

D. Giao điểm ba đường phân giác của tam giác.

Hướng dẫn giải

Đáp án đúng là: D

Gọi A, B, C là giao điểm của các đường bờ biển.

Gọi D là vị trí ngọn hải đăng cần đặt.

Để hải đăng cách đều ba đường bở biển thì D phải cách đều ba cạnh AB, BC và AC.

Khi đó D là giao điểm ba đường phân giác của ΔABC.

Vậy vị trí của hải đăng để khoảng cách từ đó đến ba đường bờ biển bằng nhau là giao điểm ba đường phân giác của tam giác.

Câu 16. Cho tam giác MNP có số đo như hình vẽ:

Có bao nhiêu khẳng định đúng trong các khẳng định sau:

(I). $\hat{M}$ = 80°.

(II). Tam giác MNP là tam giác nhọn.

(III). Tam giác MNP là tam giác vuông.

(IV). NP là cạnh huyền của tam giác MNP.

A. 1;

B. 2;

C. 3;

D. 4.

Hướng dẫn giải

Đáp án đúng là: B

Áp dụng định lý về tổng số đo ba góc của tam giác ta có:

$\hat{M} + \hat{N} + \hat{P}$ = 180 $°$

Suy ra $\hat{M} = 180 ° - \hat{N} - \hat{P} = 180 ° - 37 ° - 53 ° = 90 °$

Suy ra tam giác MNP vuông tại M

Ta có cạnh NP là cạnh đối diện với góc vuông M nên NP là cạnh huyền

Suy ra các khẳng định (III), (IV) đúng. Các khẳng định (I), (II) sai.

Vậy có 2 khẳng định đúng.

Câu 17. Tính số đo x trong hình sau:

A. 38°;

B. 52°;

C. 36°;

D. 62°.

Hướng dẫn giải

Đáp án đúng là: A

Ta có: $\hat{H G K}$ + $\hat{K G I}$ = $\hat{H G I}$

Suy ra $\hat{K G I}$ = $\hat{H G I}$ − $\hat{H G K}$ = 90° − 38° = 52°

Vì tam giác GKI vuông tại K nên $\hat{K G I}$ + $\hat{G I K}$ = 90°

Suy ra $\hat{G I K}$ = 90° − $\hat{K G I}$ = 90° − 52° = 38°

Vậy x = 38°.

Câu 18. Trong các bộ ba đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

A. 2 cm; 3 cm; 6 cm;

B. 3 cm; 6 cm; 3 cm;

C. 3 cm; 4 cm; 5 cm;

D. 5 cm; 6 cm; 7 dm.

Hướng dẫn giải

Đáp án đúng là: C

+ Xét bộ ba: 2 cm; 3 cm; 6 cm

Ta có 2 cm + 3 cm = 5 cm < 6 cm

Suy ra bộ ba đoạn thẳng có độ dài: 2 cm; 3 cm; 6 cm không lập thành một tam giác.

+ Xét bộ ba: 3 cm; 6 cm; 3 cm

Ta có 3 cm + 3 cm = 6 cm

Suy ra bộ ba đoạn thẳng có độ dài: 3 cm; 6 cm; 3 cm không lập thành một tam giác.

+ Xét bộ ba: 3 cm; 4 cm; 5 cm

Ta có: 4 cm – 3 cm < 5 cm < 4 cm + 3 cm.

Suy ra bộ ba đoạn thẳng có độ dài: 3 cm; 4 cm; 5 cm lập thành một tam giác.

+ Xét bộ ba: 5 cm; 6 cm; 7 dm

Ta có 7 dm = 70 cm.

Vì 5 cm + 6 cm < 70 cm.

Suy ra bộ ba đoạn thẳng có độ dài: 5 cm; 6 cm; 7 dm không lập thành một tam giác.

Câu 19. Cho tam giác ABC có AB = 2, BC = 8 cm. Biết độ dài cạnh AC là một số nguyên tố. Chu vi tam giác ABC là:

A. 18 cm;

B. 7 cm;

C. 17 cm;

D. 19 cm.

Hướng dẫn giải

Đáp án đúng là: C

Gọi độ dài cạnh AC là x (x > 0) (cm)

Từ bất đẳng thức trong tam giác, ta có: BC – AB < AC < BC + AB

Suy ra 8 – 2 < x < 8 + 2

Suy ra 6 < x < 10

Suy ra x ∈ {7; 8; 9}

Vì x là một số nguyên tố

Suy ra x = 7

Suy ra AC = 7 (cm)

Chu vi tam giác ABC bằng:

AB + AC + BC = 2 + 7 + 8 = 17 (cm).

Vậy chu vi tam giác ABC là 17 cm.

Câu 20: Cho ∆ABC = ∆MNP. Biết AB = 7 cm, MP = 10 cm và chu vi của tam giác 24 cm. Tính các cạnh còn lại của mỗi tam giác.

A. MN = AC = 7 cm; BC = NP = 10 cm;

B. MN = AC = 10 cm; BC = NP = 7 cm;

C. MN = 7 cm; AC = 10 cm; BC = NP = 7 cm;

D. MN = 10 cm; AC = 7 cm; BC = NP = 7 cm.

Hướng dẫn giải

Đáp án đúng là: C

Ta có ∆ABC = ∆MNP nên AB = MN = 7cm, AC = MP = 10cm, BC = NP (các cạnh tương ứng bằng nhau)

Chu vi tam giác ABC là: AB + AC + BC = 24 (cm).

Nên BC = 24 – (AB + AC)

= 24 – (7 + 10) = 24 – 17 = 7 (cm).

Suy ra NP = BC = 7 cm.

Vậy MN = 7 cm; AC = 10 cm; BC = NP = 7 cm.

Câu 21. Tính số đo x trên hình vẽ sau:

A. x = 45°;

B. x = 40°;

C. x = 35°;

D. x = 70°.

Hướng dẫn giải

Đáp án đúng là: C

Ta có tam giác ABC cân tại A (vì AB = AC) có $\hat{A}$ = 40° .

nên $\hat{B} = \hat{A C B}$ = $\frac{180 ° - 40}{2}$ = 70°.

Ta có $\hat{A C B}$ + $\hat{A C D}$ = 180° (hai góc kề bù).

suy ra $\hat{A C D}$ = 180° − $\hat{A C B}$ = 180° − 70° = 110°.

Ta lại có tam giác CAD cân tại C (vì CA = CD) có $\hat{A C D}$ = 110°.

Nên x = $\hat{C D A}$ = $\hat{C A D}$ = $\frac{180 ° - 110 °}{2}$ = 35°.

Vậy x = 35°.

Câu 22. Cho tam giác ABC cân tại A có = 2α. Tính số đo góc B theo α.

Hướng dẫn giải

Đáp án đúng là: D

Do tam giác ABC cân tại A nên $\hat{B} = \hat{C}$ .

Xét tam giác ABC có:

$\hat{A} + \hat{B} + \hat{C}$ = 180° (tổng ba góc trong một tam giác).

$\hat{B} + \hat{C}$ = 180° − $\hat{A}$

Nên $\hat{B} = \hat{C} = \frac{180 ° - \hat{A}}{2}$

= $\frac{180 ° - 2 α}{2}$ = 90° − α.

Vậy $\hat{B}$ = 90° − α.

Câu 23: Cho ∆ABC = ∆DEF. Biết $\hat{A} + \hat{B} = 130 °$ ; $\hat{E} = 55 °$ . Tính $\hat{A}, \hat{C}, \hat{D}, \hat{F} .$

Hướng dẫn giải

Đáp án đúng là: C

Ta có ∆ABC = ∆DEF nên: $\hat{A} = \hat{D}; \hat{F} = \hat{C}; \hat{B} = \hat{E}$ = 55°.

Xét tam giác ABC có:

$\hat{A} + \hat{B}$ = 130° (gt)

Suy ra $\hat{A}$ = 130° − $\hat{B}$ = 130° − 55° = 75°.

Lại có $\hat{A} + \hat{B} + \hat{C}$ = 180°.

Suy ra = 180° − $(\hat{A} + \hat{B})$ = 180° − 130° = 50°.

Vậy $\hat{A} = \hat{D}$ = 75°, $\hat{F} = \hat{C}$ = 50°.

Câu 24. Trong tam giác ABC có AH vuông góc với BC (H Î BC). Chọn câu sai.

A. Nếu AB < AC thì BH < HC;

B. Nếu AB > AC thì BH < HC;

C. Nếu AB = AC thì BH = HC;

D. Nếu BH > HC thì AB > AC.

Hướng dẫn giải

Đáp án đúng là: B

Trong tam giác ABC có AH là đường vuông góc và BH;CH là hai hình chiếu.

Khi đó:

+ Nếu AB < AC thì BH < HC (câu A đúng);

+ Nếu AB > AC thì BH > HC (câu B sai);

+ Nếu AB = AC thì BH = HC (câu C đúng);

+ Nếu BH > HC thì AB > AC (câu D đúng).

Câu 25. Quan sát hình bên dưới. Có các đường xiên và đường vuông góc kẻ từ O xuống đường thẳng c, trong số các đường này đường nào ngắn nhất?

A. ON;

B. OM;

C. OP;

D. OR.

Hướng dẫn giải

Đáp án đúng là: C

Ta có: OP là đường vuông góc. OM, ON, OP, OQ, OR là các đường xiên.

Vì thế trong số các đường này, OP ngắn nhất.

Câu 26. Cho tam giác ABC vuông tại A có $\hat{A B C}$ = 60°, H là trung điểm của BC. Từ H kẻ đường vuông góc với BC cắt AC tại K. Tính $\hat{K B H}$ .

A. 30°;

B. 45°;

C. 60°;

D. 90°.

Hướng dẫn giải

Đáp án đúng là: A

Xét ∆KHB và ∆KHC cùng vuông tại H có:

KH là cạnh chung;

HB= HC (H là trung điểm của BC).

Do đó ∆KHB = ∆KHC (hai cạnh góc vuông).

Suy ra $\hat{K B H}$ = $\hat{K C H}$ (hai góc tương ứng).

Ta có : $\hat{A B C}$ + $\hat{A C B}$ = 90°(∆ABC vuông tại A) .

Suy ra $\hat{A C B}$ = 90° − $\hat{A B C}$ = 90° − 60° = 30°.

Ta có: $\hat{K C H}$ = $\hat{A C B}$ = 30°( K $\in$ AC; H $\in$ BC);

$\hat{K B H}$ = $\hat{K C H}$ (cmt).

Suy ra $\hat{K B H}$ = 30°.

Câu 27. Cho tam giác ∆ABC có $\hat{A}$ là góc tù. Các đường trung trực của AB và AC cắt nhau tại O. Đường tròn tâm O bán kính OA đi qua điểm:

A. B và C;

B. M và N;

C. B;

D. C.

Hướng dẫn giải

Đáp án đúng là: A

Gọi M và N lần lượt là trung điểm của AB và AC.

Xét ∆ABC có:

OM là đường trung trực của AB;

ON là đường trung trực của AC;

OM và ON cắt nhau tại O.

Suy ra O cách đều ba đỉnh ∆ABC.

Do đó OA = OB = OC

Vậy đường tròn tâm O bán kính OA đi qua các điểm B và C.

Câu 28. Cho tam giác ∆ABC có M và N lần lượt là trung điểm của AB, BC. Từ M và N vẽ 2 đường trung trực cắt nhau tại O. Biết đường tròn tâm O bán kính OA có đường kính bằng 8 cm. Độ dài đoạn thẳng OB bằng:

A. 2 cm;

B. 4 cm;

C. 8 cm;

D. 5 cm.

Hướng dẫn giải

Đáp án đúng là: B

Xét ∆ABC có:

OM là đường trung trực của AB (gt);

ON là đường trung trực của BC (gt);

OM và ON cắt nhau tại O.

Do đó O cách đều ba đỉnh của ∆ABC.

Suy ra OA = OB = OC.

Ta có: Đường tròn tâm O bán kính OA có đường kính bằng 8 cm.

Suy ra: OA = 4 (cm).

Mà OA = OB (cmt).

Nên OB = 4 (cm).

Vậy độ dài đoạn thẳng OB bằng 4 cm.

Câu 29. Cho tam giác ∆ABC có đường trung tuyến BD bằng đường trung tuyến CF. Khi đó tam giác ∆ABC là:

A.Tam giác vuông;

B. Tam giác vuông cân;

C.Tam giác thường;

D.Tam giác cân.

Hướng dẫn giải

Đáp án đúng là: D

Xét ∆ABC có:

BE là đường trung tuyến (E là trung điểm của AC);

CF là đường trung tuyến (F là trung điểm của AB);

BE và CF cắt nhau tại G.

Do đó G là trọng tâm của ∆ABC.

Suy ra $\frac{B G}{B D} = \frac{2}{3}$ ; $\frac{C G}{C F}$ = $\frac{2}{3}$

mà BD = CF (gt) nên BG = CG.

Do vậy FG = GD.

Xét ∆FGB và ∆DGC có:

BG = CG (cmt);

FG = GD (cmt);

$\hat{F G B}$ = $\hat{D G C}$ ( hai góc đối đỉnh).

Do đó ∆FGB = ∆DGC (c.g.c).

Suy ra BF = DC (hai cạnh tương ứng)

Ta có : AB = $\frac{1}{2}$ BF (F là trung điểm của AB);

AC= $\frac{1}{2}$ DC ( D là trung điểm của AC);

BF = DC (cmt).

Do đó AB = AC.

Vậy ∆ABC là tam giác cân tại A.

Câu 30. Cho hình vẽ như bên dưới. Biết đường kính của đường tròn nằm trong tam giác là 8 cm. Độ dài của GK bằng:

A. 8 cm;

B. 2 cm;

C. 4 cm;

D. 5 cm.

Hướng dẫn giải

Đáp án đúng là: C

Xét ΔABC có G là giao điểm của ba đường phân giác.

Do đó G là tâm của đường tròn ngoại tiếp có bán kính GK.

Suy ra GK = 8 : 2 = 4 (cm).

Vậy độ dài đoạn thẳng GK bằng 4 cm.

Xem thêm các bài trắc nghiệm Toán 7 Chân trời sáng tạo hay, chi tiết khác:

Trắc nghiệm Toán 7 Bài 9: Tính chất ba đường phân giác của tam giác

Trắc nghiệm Ôn tập chương 8

Trắc nghiệm Toán 7 Bài 1: Làm quen với biến cố ngẫu nhiên

Trắc nghiệm Toán 7 Bài 2: Làm quen với xác suất của biến cố ngẫu nhiên

Trắc nghiệm Ôn tập chương 9
Sách bài tập Toán 7 (Chân trời sáng tạo): Bài tập cuối chương 8 trang 65, 66

Giải SBT Toán lớp 7 Bài tập cuối chương 8 trang 65, 66

Giải trang 65 Tập 2

Bài 1 trang 65 Tập 2: Cho tam giác ABC có $\hat{A} = \hat{B} + \hat{C}$ . Hai đường phân giác của góc B và C cắt nhau tại O.

a) Tính số đo góc A

b) Tính số đo góc BOC.

Lời giải:

a) Trong ∆CAB ta có: $\hat{A} + \hat{A B C} + \hat{A C B} = 180 °$ (tổng ba góc trong một tam giác).

Mà $\hat{A} = \hat{A B C} + \hat{A C B}$ (giả thiết).

Suy ra $\hat{A} = \hat{A B C} + \hat{A C B} = \frac{180 °}{2} = 90 °$ .

Vậy $\hat{A} = 90 ° .$

b) Vì BO là phân giác của góc ABC nên $\hat{A B O} = \hat{C B O} = \frac{\hat{A B C}}{2}$

Vì CO là phân giác của góc ACB nên $\hat{A C O} = \hat{B C O} = \frac{\hat{A C B}}{2}$

Trong ∆COB ta có: $\hat{B O C} + \hat{O B C} + \hat{O C B} = 180 °$ (tổng ba góc trong một tam giác).

Mà $\hat{C B O} = \frac{\hat{A B C}}{2}$ , $\hat{B C O} = \frac{\hat{A C B}}{2}$ , $\hat{A B C} + \hat{A C B} = 90 °$ .

Suy ra

$\hat{B O C} = 180 ° - \frac{\hat{A B C} + \hat{A C B}}{2} = 180 ° - \frac{90 °}{2} = 135 °$

Vậy $\hat{B O C} = 135 ° .$

Bài 2 trang 65 Tập 2: Cho tam giác ABC có M là điểm đồng quy của ba đường phân giác. Qua M vẽ đường thẳng song song với BC và cắt AB, AC lần lượt tại N và P. Chứng minh rằng NP = BN + CP.

Lời giải:

•Ta có: MN // BC (giả thiết) do đó $\hat{M_{1}} = \hat{B_{1}}$ (hai góc so le trong).

Vì BM là phân giác của góc ABC nên $\hat{B_{1}} = \hat{B_{2}} = \frac{\hat{A B C}}{2}$ .

Suy ra $\hat{M_{1}} = \hat{B_{2}}$ nên tam giác BNM cân tại N.

Do đó BN = NM.

•Ta có: MP // BC (giả thiết) do đó $\hat{M_{2}} = \hat{C_{2}}$ (hai góc so le trong).

Vì CM là phân giác của góc ACB nên $\hat{C_{1}} = \hat{C_{2}} = \frac{\hat{A C B}}{2}$ .

Suy ra $\hat{M_{2}} = \hat{C_{1}}$ nên tam giác CMP cân tại P.

Do đó PM = PC.

Ta có: NP = MN + MP = BN + CP.

Vậy NP = BN + CP.

Bài 3 trang 65 Tập 2: Cho tam giác ABC có M là giao điểm của hai phân giác của góc B và góc C. Cho biết $\hat{B M C} = 132 °$ . Tính số đo các góc $\hat{M A B}$ và $\hat{M A C}$ .

Lời giải:

Trong DCMBcó: $\hat{B M C} + \hat{M B C} + \hat{M C B} = 180 °$ (tổng ba góc trong một tam giác).

Suy ra

$\hat{M B C} + \hat{M C B} = 180 ° - \hat{B M C} = 180 ° - 132 ° = 48 °$ .

Vì BM là phân giác của góc ABC nên $\hat{A B C} = 2 \hat{M B C}$ .

Vì CM là phân giác của góc ACB nên $\hat{A C B} = 2 \hat{M C B}$ .

Suy ra

$\hat{A B C} + \hat{A C B} = 2 (\hat{M B C} + \hat{M C B}) = 2.48 ° = 96 °$ .

Trong ∆CAB ta có: $\hat{B A C} + \hat{A B C} + \hat{A C B} = 180 °$ (tổng ba góc trong một tam giác).

Suy ra

$\hat{B A C} = 180 ° - (\hat{A B C} + \hat{A C B}) = 180 ° - 96 ° = 84 °$ .

Do AM là phân giác góc A của tam giác ABC nên ta có:

$\hat{M A B} = \hat{M A C} = \frac{\hat{B A C}}{2} = \frac{84 °}{2} = 42 °$ .

Vậy $\hat{M A B} = \hat{M A C} = 42 ° .$

Bài 4 trang 65 Tập 2: Cho tam giác ABC có AB > AC. Trên tia đối của tia BC lấy điểm M sao cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA.

a) Hãy so sánh các góc $\hat{A M B}$ và $\hat{A N C}$ .

b) Hãy so sánh các đoạn AM và AN.

Lời giải:

a) Xét ∆ABC có AB > AC (giả thiết) nên $\hat{C_{1}} > \hat{B_{1}}$ (trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn) (1)

Vì CN = CA (giả thiết) nên tam giác ANC cân tại C.

Suy ra $\hat{A N C} = \hat{N A C}$ (tính chất tam giác cân).

Mặt khác $\hat{A N C} + \hat{N A C} + {\hat{C}}_{2} = 180 °$ (tổng ba góc trong tam giác CAN).

Do đó ${\hat{C}}_{2} = 180 ° - 2 \hat{A N C}$

Mà ${\hat{C}}_{1} + {\hat{C}}_{2} = 180^{o}$ (hai góc kề bù) nên ${\hat{C}}_{2} = 180^{o} - {\hat{C}}_{1}$

Suy ra ${\hat{C}}_{1} = 2 \hat{A N C}$ (2)

Tương tự với tam giác BAM ta có: $\hat{B_{1}} = 2 \hat{A M B}$ (3).

Từ (1),(2),(3) suy ra $\hat{A N C} > \hat{A M B}$ .

Vậy $\hat{A N C} > \hat{A M B}$ .

b) Xét tam giác ANM có $\hat{A N M} > \hat{A M N}$ (do $\hat{A N C} > \hat{A M B}$ )

Do đó AM > AN (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn).

Vậy AM > AN.

Bài 5 trang 65 Tập 2: Cho hai đoạn thẳng AB và CD cắt nhau tại O. Tìm điểm M sao cho: MA + MB + MC + MD nhỏ nhất.

Lời giải:

Xét ∆ABM có: MA + MB ≥ AB (bất đẳng thức trong tam giác)

Xét ∆CDM có: MC + MD ≥ CD (bất đẳng thức trong tam giác)

Suy ra MA + MB + MC + MD ≥ AB + CD.

Nên MA + MB + MC + MD nhỏ nhất khi và chỉ khi:

MA + MB + MC + MD = AB + CD

Khi đó MA + MB = ABvà MC + MD = CD

Điều này chỉ xảy ra khi M trùng với điểm O.

Vậy khi điểm M là giao điểm của AB và CD thì MA + MB + MC + MD nhỏ nhất.

Bài 6 trang 65 Tập 2: a) Chứng minh trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ cùng một đỉnh.

b) Chứng minh trong một tam giác, đường cao không lớn hơn đường phân giác xuất phát từ cùng một đỉnh.

Lời giải:

a) Cho tam giác ABC. Vẽ đường cao AH và đường trung tuyến AM.

Ta có AH là đường vuông góc, AM là đường xiên.

Suy ra AH ≤ AM (mối quan hệ giữa đường vuông góc và đường xiên).

Vậy trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ cùng một đỉnh.

b) Cho tam giác ABC. Vẽ đường cao AH và đường phân giác AD.

Ta có AH là đường vuông góc, AD là đường xiên.

Suy ra AH ≤ AD (mối quan hệ giữa đường vuông góc và đường xiên).

Vậy trong một tam giác, đường cao không lớn hơn đường phân giác xuất phát từ cùng một đỉnh.

Giải trang 66 Tập 2

Bài 7 trang 66 Tập 2: Cho tam giác ABC có ba đường phân giác AD, BE, CF đồng quy tại I. Vẽ IH vuông góc với BC tại H. Chứng minh rằng $\hat{B I H} = \hat{C I D} .$

Lời giải:

Vì BI là phân giác của góc ABC nên $\hat{A B I} = \hat{I B C} = \frac{\hat{A B C}}{2}$ .

Vì CI là phân giác của góc ACB nên $\hat{A C I} = \hat{B C I} = \frac{\hat{A C B}}{2}$ .

Vì AI là phân giác của góc ACB nên $\hat{B A I} = \hat{C A I} = \frac{\hat{C A B}}{2}$ .

Ta có: $\hat{D I C} + \hat{A I C} = 180 °$ (hai góc kề bù).

Do đó $\hat{D I C} = 180 ° - \hat{A I C}$ (1)

Trong ∆AIC có $\hat{I A C} + \hat{I C A} + \hat{A I C} = 180 °$ (tổng ba góc trong một tam giác).

Suy ra $\hat{I A C} + \hat{I C A} = 180 ° - \hat{A I C}$ (2)

Từ (1) và (2) ta có:

Nên $\hat{D I C} = \hat{I A C} + \hat{I C A} = \frac{\hat{B A C} + \hat{B C A}}{2}$ .

Trong ∆CAB ta có: $\hat{B A C} + \hat{A B C} + \hat{A C B} = 180 °$ (tổng ba góc trong một tam giác)

Nên $\hat{B A C} + \hat{A C B} = 180 ° - \hat{A B C}$

Suy ra

$\hat{D I C} = \frac{\hat{B A C} + \hat{B C A}}{2} = \frac{180 ° - \hat{A B C}}{2} = 90 ° - \frac{\hat{A B C}}{2}$ (3)

Vì tam giác BIH vuông tại H nên $\hat{H I B} + \hat{H B I} = 90 °$ .

Suy ra $\hat{H I B} = 90 ° - \hat{H B I} = 90 ° - \frac{\hat{A B C}}{2}$ (4)

Từ (3) và (4) suy ra $\hat{B I H} = \hat{C I D}$ .

Vậy $\hat{B I H} = \hat{C I D}$ .

Bài 8 trang 66 Tập 2: Cho tam giác ABC cân tại A và cho $\hat{A} = 124 ° .$ Vẽ đường cao BH và phân giác BK ứng với đỉnh B của tam giác ABC. Tính số đo các góc của tam giác BHK.

Lời giải:

Vì tam giác ABC cân tại A (giả thiết)

Nên $\hat{A B C} = \hat{A C B}$ (tính chất tam giác cân)

Trong ∆CAB ta có: $\hat{B A C} + \hat{A B C} + \hat{A C B} = 180 °$ (tổng ba góc trong một tam giác).

Mà $\hat{B A C} = 124 °$ (giả thiết), $\hat{A B C} = \hat{A C B}$ (chứng minh trên).

Suy ra

$\hat{A B C} = \hat{A C B} = \frac{180 ° - \hat{B A C}}{2} = \frac{180 ° - 124 °}{2} = 28 °$ .

Vì BK là phân giác của góc ABC nên $\hat{A B K} = \hat{K B C} = \frac{\hat{A B C}}{2} = \frac{28 °}{2} = 14 °$ .

Trong ∆KAB ta có: $\hat{A B K} + \hat{K A B} + \hat{A K B} = 180 °$ (tổng ba góc trong một tam giác).

Suy ra

$\hat{A K B} = 180 ° - \hat{A B K} - \hat{K A B} = 180 ° - 14 ° - 124 ° = 42 °$ .

Vì tam giác BKH vuông tại H nên $\hat{K H B} = 90 °$ và $\hat{H K B} + \hat{H B K} = 90 °$ .

Suy ra $\hat{H B K} = 90 ° - \hat{H K B} = 90 ° - 42 ° = 48 °$ .

Vậy tam giác BHK có $\hat{H B K} = 48 °, \hat{B K H} = 42 °, \hat{K H B} = 90 ° .$

Bài 9 trang 66 Tập 2: Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Chứng minh AH là đường trung trực của BC.

Lời giải:

Tam giác ABC có hai đường cao BE và CF cắt nhau tại H nên H là trực tâm của tam giác.

Do đó AH là đường cao ứng với cạnh BC.

Kéo dài AH cắt BC tại M.

Khi đó AH ⊥ BC tại M (1)

Vì tam giác ABC cân tại A (giả thiết) nên AB = AC.

Xét ΔBMA và ΔCMA có:

$\hat{B M A} = \hat{C M A} (= 90 °)$ ,

AM là cạnh chung,

AB = AC (chứng minh trên)

Do đó ΔBMA = ΔCMA (cạnh huyền – cạnh góc vuông).

Suy ra BM = CM (hai cạnh tương ứng)(2)

Từ (1) và (2) suy ra AH ⊥ BC tại trung điểm M của BC.

Do đó AH là đường trung trực của BC.

Vậy AH là đường trung trực của BC.

Bài 10 trang 66 Tập 2: Cho tam giác nhọn ABC. Hãy nêu cách tìm các điểm sau đây bên trong tam giác ABC.

a) Điểm M cách đều ba đỉnh của tam giác ABC.

b) Điểm N cách đều ba cạnh của tam giác ABC.

c) Điểm P là trọng tâm của tam giác ABC.

d) Điểm Q là trực tâm của tam giác ABC.

Lời giải:

a) Điểm M cách đều ba đỉnh của tam giác ABC nên điểm M là giao điểm của ba đường trung trực của tam giác ABC.

Do ba đường trung trực của một tam giác luôn đi qua một điểm, nên giao điểm của hai trong ba đường trung trực cũng thuộc đường trung trực còn lại.

Ta vẽ hai đường trung trực của AB và BC, giao điểm của hai đường trung trực đó là điểm M (hình vẽ).

b) Điểm N cách đều ba cạnh của tam giác ABC nên điểm N là giao điểm của ba đường phân giác trong của tam giác ABC.

Do ba đường phân giác của một tam giác luôn đi qua một điểm, nên giao điểm của hai trong ba đường phân giác cũng thuộc đường phân giác còn lại.

Ta vẽ hai đường phân giác của góc A và góc B, giao điểm của hai đường phân giác này là điểm N (hình vẽ).

c) Điểm P là trọng tâm của tam giác ABC nên điểm P là giao điểm của ba đường trung tuyến của tam giác ABC.

Do ba đường trung tuyến của một tam giác luôn đi qua một điểm, nên giao điểm của hai trong ba đường trung tuyến cũng thuộc đường trung tuyến còn lại.

Ta vẽ hai đường trung tuyến xuất phát từ đỉnh A và C của tam giác, giao điểm của hai đường trung tuyến này là điểm P (hình vẽ).

d) Điểm Q là trực tâm của tam giác ABC nên điểm Q là giao điểm của ba đường cao của tam giác ABC.

Do ba đường cao của một tam giác luôn đi qua một điểm, nên giao điểm của hai trong ba đường cao cũng thuộc đường cao còn lại.

Ta vẽ hai đường cao xuất phát từ đỉnh A và đỉnh B của tam giác, giao điểm của hai đường cao này là trực tâm Q của tam giác (hình vẽ).

Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 9: Tính chất ba đường phân giác của tam giác

Bài tập cuối chương 8

Bài 1: Làm quen với biến cố ngẫu nhiên

Bài 2: Làm quen với xác suất của biến cố ngẫu nhiên

Bài tập cuối chương 9
Giải SGK Toán 7 (Chân trời sáng tạo): Bài tập cuối chương 8 trang 84

Giải bài tập Toán lớp 7 Bài tập cuối chương 8 trang 84

Bài 1 trang 84 Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A ( $\hat{A} < 90 °$ ). Hai đường cao BE và CF cắt nhau tại H.

a) Chứng minh rằng $Δ B E C = Δ C F B$ .

b) Chứng minh rằng $Δ A H F = Δ A H E$ .

c) Gọi I là trung điểm của BC. Chứng minh rằng ba điểm A, H, I thẳng hàng.

Lời giải:

a) Tam giác ABC cân tại A nên $\hat{A B C} = \hat{A C B}$ và AB = AC.

Xét $Δ B E C$ vuông tại E và $Δ C F B$ vuông tại F có:

$\hat{E C B} = \hat{F B C}$ (chứng minh trên).

BC chung.

Do đó $Δ B E C = Δ C F B$ (cạnh huyền – góc nhọn).

b) Do $Δ B E C = Δ C F B$ (cạnh huyền – góc nhọn) nên EC = FB (2 cạnh tương ứng).

Mà AB = AC nên AB – FB = AC – EC hay AF = AE.

Xét $Δ A H F$ vuông tại F và $Δ A H E$ vuông tại E có:

AF = AE (chứng minh trên).

AH chung.

Do đó $Δ A H F = Δ A H E$ (cạnh huyền – cạnh góc vuông).

c) DABC có hai đường cao BE, CF cắt nhau tại H nên H là trực tâm của $△$ ABC.

Suy ra AH $⊥$ BC (1).

Xét $△$ AIB và $△$ AIC có:

AB = AC (chứng minh trên).

IB = IC (do I là trung điểm của BC).

AI chung.

Suy ra $△$ AIB = $△$ AIC (c.c.c).

Do đó $\hat{A I B} = \hat{A I C}$ (2 góc tương ứng).

Mà $\hat{A I B} + \hat{A I C} = 180 °$ nên $\hat{A I B} + \hat{A I B} = 180 °$ hay $2 \hat{A I B} = 180 °$ .

Suy ra $\hat{A I B} = \hat{A I C} = 90 °$ .

Do đó AI $⊥$ BC (2).

Từ (1) và (2) suy ra A, H, I thẳng hàng.

Bài 2 trang 84 Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A, vẽ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.

a) Chứng minh rằng tam giác ABM cân.

b) Chứng minh rằng $Δ A B C = Δ M B C$ .

Lời giải:

a) Xét $Δ A H B$ vuông tại H và $Δ M H B$ vuông tại H có:

AH = MH (theo giả thiết).

BH chung.

Do đó $Δ A H B = Δ M H B$ (2 cạnh góc vuông).

Suy ra AB = MB (2 cạnh tương ứng).

Tam giác ABM có AB = MB nên tam giác ABM cân tại B.

b) Do $Δ A H B = Δ M H B$ (2 cạnh góc vuông) nên $\hat{A B H} = \hat{M B H}$ (2 góc tương ứng).

Xét $Δ A B C$ và $Δ M B C$ có:

AB = MB (chứng minh trên).

$\hat{A B C} = \hat{M B C}$ (chứng minh trên).

BC chung.

Do đó $Δ A B C = Δ M B C$ (c – g – c).

Bài 3 trang 84 Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia đối của tia HC lấy điểm D sao cho HD = HC.

a) Chứng minh rằng AC = AD.

b) Chứng minh rằng $\hat{A D B} = \hat{B A H}$ .

Lời giải:

a) Trên tia đối của HC lấy D sao cho HC = HD nên H là trung điểm của CD.

AH $⊥$ CD tại trung điểm H của CD nên AH là đường trung trực của CD.

Do đó AC = AD.

b) Tam giác ACD có AC = AD nên tam giác ACD cân tại A.

Do đó $\hat{A D B} = \hat{A C B}$ .

Trong tam giác ABC vuông tại A: $\hat{A C B} + \hat{A B C} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng $90 °$ ).

Suy ra $\hat{A C B} = 90 ° - \hat{A B C}$ .

Trong tam giác ABH vuông tại H: $\hat{B A H} + \hat{A B H} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng $90 °$ ).

Suy ra $\hat{B A H} = 90 ° - \hat{A B H}$ .

Do đó $\hat{A C B} = \hat{B A H}$ .

Mà $\hat{A C B} = \hat{A D B}$ nên $\hat{A D B} = \hat{B A H}$ .

Bài 4 trang 84 Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ BE $⊥$ AN (E $\in$ AN).

a) Chứng minh BE là tia phân giác của góc ABN.

b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của AH với BE. Chứng minh rằng NK // CA.

c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB với NF. Chứng minh rằng tam giác GBC cân.

Lời giải:

a) Xét $△$ BEA vuông tại E và $△$ BEN vuông tại E có:

BA = BN (theo giả thiết).

BE chung.

Suy ra $△$ BEA = $△$ BEN (cạnh huyền – cạnh góc vuông).

Do đó $\hat{E B A} = \hat{E B N}$ (2 góc tương ứng).

Mà BE nằm trong $\hat{A B N}$ nên BE là tia phân giác của $\hat{A B N} .$

b) Tam giác BAN có hai đường cao AH và BE cắt nhau tại K nên K là trực tâm của tam giác BAN.

Do đó NK $⊥$ AB.

Mà AC $⊥$ AB nên NK // AC.

c) Do BE là tia phân giác của $\hat{A B N}$ nên $\hat{A B E} = \hat{N B E}$ .

Xét $Δ A B F$ và $Δ N B F$ có:

AB = NB (theo giả thiết).

$\hat{A B F} = \hat{N B F}$ (chứng minh trên).

BF chung.

Do đó $Δ A B F = Δ N B F$ (c.g.c).

Suy ra AF = NF (2 cạnh tương ứng) và $\hat{B A F} = \hat{B N F} = 90 °$ (2 góc tương ứng).

Do đó FN $⊥$ BC.

Xét $Δ A F G$ vuông tại A và $Δ N F C$ vuông tại N có:

AF = NF (chứng minh trên).

$\hat{A F G} = \hat{N F C}$ (2 góc đối đỉnh).

Do đó $Δ A F G = Δ N F C$ (góc nhọn – cạnh góc vuông).

Suy ra AG = NC (2 cạnh tương ứng).

Mà BA = BN nên BA + AG = BN + NC hay BG = BC.

Tam giác BGC có BG = BC nên tam giác BGC cân tại B.

Bài 5 trang 84 Toán lớp 7 Tập 2: Cho tam giác ABC nhọn (AB < AC), vẽ đường cao AH. Đường trung trực của cạnh BC cắt AC tại M, cắt BC tại N.

a) Chứng minh rằng $\hat{B M N} = \hat{H A C}$ .

b) Kẻ MI $⊥$ AH (I $\in$ AH), gọi K là giao điểm của AH với BM. Chứng minh rằng I là trung điểm của AK.

Lời giải:

a) Do M nằm trên đường trung trực của BC nên MB = MC.

Xét $Δ B M N$ vuông tại N và $Δ C M N$ vuông tại N có:

MB = MC (chứng minh trên).

MN chung.

Do đó $Δ B M N = Δ C M N$ (cạnh huyền – cạnh góc vuông).

Suy ra $\hat{B M N} = \hat{C M N}$ (2 góc tương ứng) (1).

Do MN $⊥$ BC, AH $⊥$ BC nên MN // AH.

Do đó $\hat{C M N} = \hat{H A C}$ (2 góc đồng vị) (2).

Từ (1) và (2) suy ra $\hat{B M N} = \hat{H A C}$ .

b) Do $Δ B M N = Δ C M N$ (cạnh huyền – cạnh góc vuông) nên $\hat{M B N} = \hat{M C N}$ (2 góc tương ứng).

Do MI $⊥$ AH, BC $⊥$ AH nên MI // BC.

Do đó $\hat{A M I} = \hat{M C N}$ (2 góc đồng vị) và $\hat{K M I} = \hat{M B N}$ (2 góc so le trong).

Do đó $\hat{A M I} = \hat{K M I}$ .

Xét $Δ A M I$ vuông tại I và $Δ K M I$ vuông tại I có:

$\hat{A M I} = \hat{K M I}$ (chứng minh trên).

MI chung.

Do đó $Δ A M I = Δ K M I$ (góc nhọn – cạnh góc vuông).

Suy ra AI = KI (2 cạnh tương ứng).

Mà I nằm giữa A và K nên I là trung điểm của AK.

Bài 6 trang 84 Toán lớp 7 Tập 2: Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FD = FN.

a) Chứng minh rằng $Δ M F N = Δ P F D$ .

b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm của GH. Gọi K là trung điểm của DP. Chứng minh rằng ba điểm M, H, K thẳng hàng.

Lời giải:

<

a) Tam giác MNP có đường trung tuyến NF nên F là trung điểm của MP.

Do đó FM = FP.

Xét $Δ M F N$ và $Δ P F D$ có:

MF = PF (chứng minh trên).

$\hat{M F N} = \hat{P F D}$ (2 góc đối đỉnh).

FN = FD (theo giả thiết).

Do đó $Δ M F N = Δ P F D$ (c.g.c).

b) Tam giác MNP có G là giao điểm hai đường trung tuyến ME và NF nên G là trọng tâm của tam giác MNP.

Do đó NG = $\frac{2}{3}$ NF.

Suy ra GF = $\frac{1}{3}$ NF.

Do F là trung điểm của GH nên GF = HF.

Suy ra HF = $\frac{1}{3}$ NF.

Mà NF = DF nên HF = $\frac{1}{3}$ DF.

Suy ra DH = $\frac{2}{3}$ DF.

Tam giác MDP có đường trung tuyến DF và DH = $\frac{2}{3}$ DF nên H là trọng tâm của tam giác MDP.

Lại có MK là đường trung tuyến của tam giác MDP nên M, H, K thẳng hàng.

Bài 7 trang 84 Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A có AB = $\frac{1}{2}$ AC, AD là tia phân giác $\hat{B A C}$ (D $\in$ BC). Gọi E là trung điểm của AC.

a) Chứng minh rằng DE = DB.

b) AB cắt DE tại K. Chứng minh rằng tam giác DCK cân và B là trung điểm của đoạn thẳng AK.

c) AD cắt CK tại H. Chứng minh rằng AH $⊥$ KC.

Lời giải:

a) Do E là trung điểm của AC nên AE = $\frac{1}{2}$ AC.

Mà AB = $\frac{1}{2}$ AC nên AE = AB.

Do AD là tia phân giác của $\hat{B A C}$ nên $\hat{B A D} = \hat{E A D}$ .

Xét $Δ B A D$ và $Δ E A D$ có:

AB = AE (chứng minh trên).

$\hat{B A D} = \hat{E A D}$ (chứng minh trên).

AD chung.

Do đó $Δ B A D = Δ E A D$ (c.g.c).

Suy ra DB = DE (2 cạnh tương ứng).

b) Do $Δ B A D = Δ E A D$ (c.g.c) nên $\hat{A D B} = \hat{A D E}$ (2 góc tương ứng).

Mà $\hat{K D B} = \hat{C D E}$ (2 góc đối đỉnh) nên $\hat{A D B} + \hat{K D B} = \hat{A D E} + \hat{C D E}$ hay $\hat{A D K} = \hat{A D C}$ .

Xét $Δ A D K$ và $Δ A DC$ có:

$\hat{D A K} = \hat{D A C}$ (chứng minh trên).

AD chung.

$\hat{A D K} = \hat{A D C}$ (chứng minh trên).

Do đó $Δ A D K = Δ A DC$ (g.c.g).

Suy ra DK = DC (2 cạnh tương ứng) và AK = AC (2 cạnh tương ứng).

Tam giác DCK có DK = DC nên tam giác DCK cân tại D.

Do AK = AC, mà AC = 2AB nên AK = 2AB.

Mà A, B, K thẳng hàng nên B là trung điểm của AK.

c) Do AD là đường phân giác của $\hat{B A C}$ nên $\hat{B A D} = \hat{C A D}$ hay $\hat{K A H} = \hat{C A H}$ (2 góc tương ứng).

Xét $△$ KAH và $△$ CAH có:

AK = AC (chứng minh trên).

$\hat{K A H} = \hat{C A H}$ (chứng minh trên).

AH chung.

Suy ra $△$ KAH = $△$ CAH (c.g.c).

Do đó $\hat{A H K} = \hat{A H C}$ (2 góc tương ứng).

Mà $\hat{A H K} + \hat{A H C} = 180 °$ nên $\hat{A H K} + \hat{A H K} = 180 °$ hay $2 \hat{A H K} = 180 °$ .

Suy ra $\hat{A H K} = \hat{A H C} = 90 °$ .

Do đó AH $⊥$ KC.

Bài 8 trang 84 Toán lớp 7 Tập 2: Ở Hình 1, cho biết AE = AF và $\hat{A B C} = \hat{A C B}$ . Chứng minh rằng AH là đường trung trực của BC.

Lời giải:

Tam giác ABC có $\hat{A B C} = \hat{A C B}$ nên tam giác ABC cân tại A.

Do đó AB = AC.

Suy ra A nằm trên đường trung trực của BC (1).

Mà AE = AF nên AB – AE = AC – AF hay BE = CF.

Xét $Δ E B C$ và $Δ F C B$ có:

BE = CF (chứng minh trên).

$\hat{E B C} = \hat{F C B}$ (theo giả thiết).

BC chung.

Do đó $Δ E B C = Δ F C B$ (c.g.c).

Suy ra $\hat{E C B} = \hat{F B C}$ (2 góc tương ứng) hay $\hat{H C B} = \hat{H B C}$ .

Tam giác HBC có $\hat{H C B} = \hat{H B C}$ nên tam giác HBC cân tại H.

Do đó HB = HC.

Suy ra H nằm trên đường trung trực của BC (2).

Từ (1) và (2) suy ra AH là đường trung trực của BC.

Bài 9 trang 84 Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM (H $\in$ CM). Trên tia đối của tia HC lấy điểm E sao cho HE = HM.

a) Chứng minh rằng tam giác MBE cân.

b) Chứng minh rằng $\hat{E B H} = \hat{A C M}$ .

c) Chứng minh rằng $E B ⊥ B C$ .

Lời giải:

a) Trên tia đối của tia HC lấy điểm E sao cho HE = HM nên H là trung điểm của ME.

Ta thấy BH vuông góc với ME tại trung điểm H của ME nên BH là đường trung trực của ME.

Do đó BM = BE.

Tam giác MBE có BM = BE nên tam giác MBE cân tại B.

b) Trong $Δ B H M$ vuông tại H: $\hat{H B M} + \hat{B M H} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng $90 °$ ).

Suy ra $\hat{H B M} = 90 ° - \hat{B M H}$ .

Trong $Δ C A M$ vuông tại A: $\hat{A C M} + \hat{C M A} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng $90 °$ ).

Suy ra $\hat{A C M} = 90 ° - \hat{C M A}$ .

Mà $\hat{B M H} = \hat{C M A}$ (2 góc đối đỉnh) nên $\hat{H B M} = \hat{A C M}$ (1).

Xét $Δ B H E$ vuông tại H và $Δ B H M$ vuông tại H có:

BH chung.

HE = HM (theo giả thiết).

Do đó $Δ B H E = Δ B H M$ (2 cạnh góc vuông).

Suy ra $\hat{E B H} = \hat{M B H}$ (2 góc tương ứng) (2).

Từ (1) và (2) suy ra $\hat{E B H} = \hat{A C M}$ .

c) Do CM là tia phân giác của $\hat{B C A}$ nên $\hat{B C M} = \hat{A C M}$ .

Xét $Δ B H C$ vuông tại H: $\hat{H B C} + \hat{B C H} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng $90 °$ ).

Suy ra $\hat{H B C} + \hat{A C M} = 90 °$ .

Mà $\hat{E B H} = \hat{A C M}$ nên $\hat{H B C} + \hat{E B H} = 90 °$ hay $\hat{E B C} = 90 °$ .

Do đó EB $⊥$ >BC.

Bài 10 trang 84 Toán lớp 7 Tập 2: Trên đường thẳng a lấy ba điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.

Lời giải:

Xét tam giác MIK có MJ $⊥$ IK, IN $⊥$ MK.

Mà MJ cắt IN tại N nên N là trực tâm của tam giác MIK.

Do đó NK vuông góc với MI.

Xem thêm các bài giải SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết:

Giải SGK Toán 7 Bài 10 : Hoạt động thực hành và trải nghiệm: Làm giàn hoa tam giác để trang trí lớp học

Giải SGK Toán 7 : Bài tập cuối chương 8

Giải SGK Toán 7 Bài 1 : Làm quen với biến cố ngẫu nhiên

Giải SGK Toán 7 Bài 2 : Làm quen với xác suất của biến cố ngẫu nhiên

Giải SGK Toán 7 Bài 3 : Hoạt động thực hành và trải nghiệm: Nhảy theo xúc xắc
Giải SGK Toán 7 (Kết nối tri thức) Bài tập cuối chương 8
Giải bài tập Toán lớp 7 Bài tập cuối chương 8

Giải Toán 7 trang 58 Tập 2

Bài 8.12 trang 58 Toán lớp 7: Một túi đựng các quả cầu có cùng kích thước, được ghi số 5; 10; 15; 20; 30; 35; 40. Lấy ngẫu nhiên một quả cầu trong túi. Chọn từ thích hợp ( chắc chắn, không thểm ngẫu nhiên) thay vào dấu “ ?” trong các câu sau
- Biến cố A: “ Lấy được quả cầu ghi số là số chính phương” là biến cố ..?..
- Biến cố B: “ Lấy được quả cầu ghi số là số chia hết cho 3” là biến cố ..?..
- Biến cố C: “ Lấy được quả cầu ghi số là số chia hết cho 5” là biến cố ..?..
Phương pháp giải:

Biến cố chắc chắn: Là biến cố biết trước được luôn xảy ra

Biến cố không thể: Là biến cố biết trước được không bao giờ xảy ra

Biến cố ngẫu nhiên: Là biến cố không thể biết trước được có xảy ra hay không

Lời giải:

Biến cố A: “ Lấy được quả cầu ghi số là số chính phương” là biến cố không thể vì trong số các số được ghi không có số nào là số chính phương.

Biến cố B: “ Lấy được quả cầu ghi số là số chia hết cho 3” là biến cố ngẫu nhiên vì trong số các số được ghi, có số 15, 30 chia hết cho 3.

Biến cố C: “ Lấy được quả cầu ghi số là số chia hết cho 5” là biến cố chắc chắn vì tất cả các số được ghi đều chia hết cho 5.

Bài 8.13 trang 58 Toán lớp 7: Một thùng kín đựng 5 quả bóng màu đỏ, 10 quả bóng màu xanh, 20 quả bóng màu vàng, có cùng kích thước. Ngọc lấy ngẫu nhiên một quả bóng trong thùng. Hỏi khả năng Ngọc lấy quả bóng màu gì lớn nhất?

Phương pháp giải:

Số bóng màu nào nhiều hơn thì khả năng lấy được bóng màu đó càng lớn.

Lời giải:

Vì số bóng màu vàng nhiều nhất nên khả năng Ngọc lấy quả bóng màu vàng lớn nhất

Bài 8.14 trang 58 Toán lớp 7: Một chiếc hộp đựng 7 tấm thẻ như nhau được ghi số 2;3;4;5;6;7;8. Rút ngẫu nhiên một tấm thẻ trong hộp. Tìm xác suất để rút được tấm thẻ

a) Ghi số nhỏ hơn 10

b) Ghi số 1

c) Ghi số 8

Phương pháp giải:

Biến cố chắc chắn: Là biến cố biết trước được luôn xảy ra. Biến cố chắc chắn có xác suất bằng 1.

Biến cố không thể: Là biến cố biết trước được không bao giờ xảy ra. Biến cố không thể có xác suất bằng 0.

Biến cố ngẫu nhiên: Có k biến cố đồng khả năng và luôn xảy ra 1 trong k biến cố này thì xác suất của mỗi biến cố đó là $\frac{1}{k}$

Lời giải:

a) Vì biến cố: “ Rút được tấm thẻ ghi số nhỏ hơn 10” là biến cố chắc chắn nên xác suất rút được tấm thẻ ghi số nhỏ hơn 10 là 1.

b) Vì biến cố: “ Rút được tấm thẻ ghi số 1” là biến cố không thể nên xác suất rút được tấm thẻ ghi số 1 là 0.

c) Biến cố: “ Rút được tấm thẻ ghi số 8” là biến cố ngẫu nhiên.

Có 7 biến cố đồng khả năng: “ Rút được thẻ ghi số 2” ; “ Rút được thẻ ghi số 3”; “ Rút được thẻ ghi số 4”; “ Rút được thẻ ghi số 5”; “ Rút được thẻ ghi số 6”; “ Rút được thẻ ghi số 7”; “ Rút được thẻ ghi số 8” và luôn xảy ra 1 trong 7 biến cố đó.

Xác suất của mỗi biến cố là: $\frac{1}{7}$

Vậy xác suất rút được thẻ ghi số 8 là $\frac{1}{7}$

Bài 8.15 trang 58 Toán lớp 7: Một tấm bìa cứng hình tròn được chia làm 8 phần có diện tích bằng nhau và ghi số 1;2;3;4;5;6;7;8 như Hình 8.4, được gắn vào trục quay có mũi tên ở tâm.

Bạn Việt quay tấm bìa.

a) Tìm xác suất để mũi tên chỉ vào hình quạt:

* Ghi số lẻ * Ghi số 6

b) Biết rằng nếu mũi tên dừng ở hình quạt ghi số 1 hoặc 2 thì Việt nhận được 100 điểm; dừng ở hình quạt ghi số 3 hoặc 4 thì Việt nhận được 200 điểm; dừng ở hình quạt ghi số 5 hoặc 6 thì Việt nhận được 300 điểm; dừng ở hình quạt ghi số 7 hoặc 8 thì Việt nhận được 400 điểm.

Xét các biến cố sau:

A: “ Việt nhận được 100 điểm”

B: “ Việt nhận được 200 điểm”

C: “ Việt nhận được 300 điểm”

D: “ Việt nhận được 400 điểm”
- Các biến cố A,B,C,D có đồng khả năng hay không?
- Tìm xác suất các biến cố A,B,C và D.
Phương pháp giải:

Biến cố ngẫu nhiên: Có k biến cố đồng khả năng và luôn xảy ra 1 trong k biến cố này thì xác suất của mỗi biến cố đó là $\frac{1}{k}$

Lời giải:

a) * Xét 2 biến cố: “ Mũi tên chỉ vào số lẻ” ; “ Mũi tên chỉ vào số chẵn”.

Đây là 2 biến cố đồng khả năng (đều có 4 khả năng) và luôn xảy ra 1 trong 2 biến cố đó

Xác suất của mỗi biến cố đó là $\frac{1}{2}$

* Xét 8 biến cố: “ Mũi tên chỉ vào số 1” ; “ Mũi tên chỉ vào số 2”; “ Mũi tên chỉ vào số 3” ; “ Mũi tên chỉ vào số 4”; “ Mũi tên chỉ vào số 5” ; “ Mũi tên chỉ vào số 6”; “ Mũi tên chỉ vào số 7” ; “ Mũi tên chỉ vào số 8”

Chúng là 8 biến cố đồng khả năng và luôn xảy ra 1 trong 8 biến cố đó

Xác suất của mỗi biến cố đó là $\frac{1}{8}$

b) Xét 4 biến cố: A,B,C,D

4 biến cố này là 4 biến cố đồng khả năng (đều có 2 khả năng) và luôn xảy ra 1 trong 4 biến cố đó

Xác suất của mỗi biến cố đó là $\frac{1}{4}$ .

Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung trang 56

Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác

Bài 32: Quan hệ giữa đường vuông góc và đường xiên

Bài 33: Quan hệ giữa ba cạnh của một tam giác
Sách bài tập Toán 7 (Kết nối tri thức) Ôn tập chương 8

Giải SBT Toán lớp 7 Ôn tập chương 8

Giải SBT Toán 7 trang 44 Tập 2

Câu 1 trang 44 SBT Toán 7 tập 2: Biến cố “Nhiệt độ cao nhất trong tháng Sáu năm sau tại Thành phố Hồ Chí Minh là 10 ^oC” là

A. Biến cố chắc chắn;

B. Biến cố ngẫu nhiên;

C. Biến cố không thể;

D. Biến cố đồng khả năng.

Lời giải:

Đáp án đúng là: C

Nhiệt độ vào tháng Sáu hàng năm luôn trên 23^oC.

Do đó biến cố “Nhiệt độ cao nhất trong tháng Sáu năm sau tại Thành phố Hồ Chí Minh là 10 ^oC” là biến cố không thể.

Câu 2 trang 44 SBT Toán 7 tập 2: Biến cố “Ngày mai có mưa rào và giông ở Hà Nội” là:

A. Biến cố ngẫu nhiên;

B. Biến cố chắc chắn;

C. Biến cố đồng khả năng;

D. Biến cố không thể.

Lời giải:

Đáp án đúng là: A

Biến cố “Ngày mai có mưa rào và giông ở Hà Nội” là biến cố ngẫu nhiên vì điều này không chắc có thể xảy ra.

Câu 3 trang 44 SBT Toán 7 tập 2: Hai túi I và II chứa các tấm thẻ được ghi số 3; 4; 5; 6; 7. Từ mỗi túi rút ngẫu nhiên một tấm thẻ.

a) Xác suất của biến cố “Tích hai số ghi trên hai tấm thẻ lớn hơn 8” bằng

A. 0;

B. $\frac{1}{2}$ ;

C. 1;

D. 0,25.

Đáp án đúng là: C

Lời giải:

Tích của hai số trên hai tấm thẻ nhỏ nhất là: 3 . 4 = 12.

Do đó tích của hai số ghi trên hai tấm thẻ luôn lớn hơn hoặc bằng 12 nên sẽ luôn lớn hơn 8 hay biến cố đã cho là biến cố chắc chắn.

Vậy xác suất của biến cố “Tích hai số ghi trên hai tấm thẻ lớn hơn 8” bằng 1.

b) Xác xuất của biến cố “Tổng hai số ghi trên hai tấm thẻ nhỏ hơn 5” bằng

A. 1;

B. 0;

C. 0,45;

D. 0,5.

Đáp án đúng là: B

Lời giải:

Tổng của hai số trên hai tấm thẻ nhỏ nhất là: 3 + 4 = 7.

Do đó tổng của hai số ghi trên hai tấm thẻ luôn lớn hơn hoặc bằng 7 nên biến cố đã cho là biến cố không thể.

Vậy xác suất của biến cố “Tổng hai số ghi trên hai tấm thẻ nhỏ hơn 5” bằng 0.

c) Biến cố “Hiệu hai số ghi trên hai tấm thẻ là số chẵn” là

A. Biến cố ngẫu nhiên;

B. Biến cố chắc chắn;

C. Biến cố không thể;

D. Biến cố đồng khả năng.

Đáp án đúng là: A

Lời giải:

Biến cố “Hiệu hai số ghi trên hai tấm thẻ là số chẵn” là biến cố ngẫu nhiên vì điều này không chắc có thể xảy ra. (Ví dụ hiệu của hai số 4 và 3 là 1).

Câu 4 trang 44 SBT Toán 7 tập 2: Một thùng kín có 20 quả bóng màu đỏ và 20 quả bóng màu xanh. Sơn lấy ngẫu nhiên một quả bóng trong thùng.

a) Xác suất của biến cố “Lấy được quả bóng màu xanh” bằng

A. 1;

B. $\frac{1}{2}$ ;

C. 0;

D. 0,8.

Đáp án đúng là: B

Lời giải:

Biến cố “Lấy được quả bóng màu xanh” và biến cố “Lấy được quả bóng màu đỏ” là đồng khả năng vì số bóng xanh bằng với số bóng đỏ. Vậy xác suất của biến cố “Lấy được quả bóng màu xanh” là $\frac{1}{2}$ .

b) Xác suất của biến cố “Lấy được quả bóng màu đỏ” bằng

A. 0

B. 1

C. 0,5

D. 0,2

Đáp án đúng là: C

Lời giải:

Biến cố “Lấy được quả bóng màu đỏ” và biến cố “Lấy được quả bóng màu xanh” là đồng khả năng vì số bóng đỏ bằng với số bóng xanh.

Vậy xác suất của biến cố cố “Lấy được quả bóng màu đỏ” là 0,5.

c) Xác suất của biến cố “Lấy được quả bóng màu đỏ hoặc màu xanh” bằng

A. 1

B. 0

C. 0,5

D. 0,4

Đáp án đúng là: A

Lời giải:

Trong tất cả những quả bóng ở trong thùng chỉ có hai màu đỏ và xanh.

Do đó biến cố “Lấy được quả bóng màu đỏ hoặc màu xanh” là biến cố chắc chắn.

Vậy xác suất của biến cố đã cho bằng 1.

Giải SBT Toán 7 trang 45 Tập 2

Bài 8.10 trang 45 SBT Toán 7 Tập 2: Một bài thi trắc nghiệm có 18 câu hỏi được đánh số từ 1 đến 18. Chọn ngẫu nhiên một câu hỏi trong bài thi.

a) Xét hai biến cố sau:

A: “Số thứ tự của câu hỏi được chọn là số có một chữ số”;

B: “Số thứ tự của câu hỏi được chọn là số có hai chữ số”.

Hai biến cố A và B có đồng khả năng không? Tại sao?

b) Tính xác suất của hai biến cố A và B.

Lời giải:

a) Hai biến cố A và B đồng khả năng vì số lượng câu hỏi mang số thứ tự là số có một chữ số bằng số lượng câu hỏi mang số thứ tự là số có hai chữ số và đều bằng 9 câu.

b) Biến biến cố A và B đồng khả năng.

Do đó xác suất của biến cố A và B bằng nhau và đều bằng $\frac{1}{2}$ .

Bài 8.11 trang 45 SBT Toán 7 Tập 2: Một tấm bài cứng hình tròn được chia làm tám phần có diện tích bằng nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8; được gắn vào trục quay có mũi tên ở tâm như Hình 8.3.

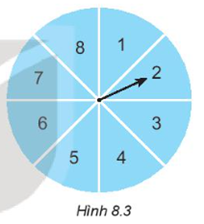
Bạn Hùng quay tấm bìa. Tính xác suất để:

a) Mũi tên dừng ở hình quạt ghi số nhỏ hơn 9;

b) Mũi tên đừng ở hình quạt ghi số 0;

c) Mũi tên dừng ở hình quạt ghi số chẵn;

d) Mũi tên dừng ở hình quạt ghi số 7 hoặc 8.

Lời giải:

a) Xác suất bằng 1 vì đây là biến cố chắc chắn (tất cả các hình quạt đều ghi số nhro hơn 9).

b) Xác suất bằng 0 vì đây là biến cố không thể (không có hình quạt nào ghi số 0).

c) Biến cố “Mũi tên dừng ở hình quạt ghi số chẵn” và biến cố “mũi tên dừng ở hình quạt ghi số lẻ” là đồng khả năng.

Vậy xác suất của biến cố cần tìm là $\frac{1}{2}$ .

d) Xét bốn biến cố sau:

A: “Mũi tên dừng ở hình quạt ghi số 1 hoặc 2”;

B: “Mũi tên dừng ở hình quạt ghi số 3 hoặc 4”;

C: “Mũi tên dừng ở hình quạt ghi số 5 hoặc 6”;

D: “Mũi tên dừng ở hình quạt ghi số 7 hoặc 8”;

Biến cố A xảy ra khi mũi tên dừng ở hình quạt ghi số 1 hoặc số 2.

Biến cố B xảy ra khi mũi tên dừng ở hình quạt ghi số 3 hoặc số 4.

Biến cố C xảy ra khi mũi tên dừng ở hình quạt ghi số 5 hoặc số 6.

Biến cố D xảy ra khi mũi tên dừng ở hình quạt ghi số 7 hoặc số 8.

Vì quay ngẫu nhiên nên mỗi hình quạt có khả năng quay được như nhau.

Do đó bốn biến cố A, B, C, D là đồng khả năng. Vì luôn xảy ra duy nhất một trong bốn biến cố này nên xác suất của biến cố D là $\frac{1}{4}$ .

Vậy xác suất của biến cố “Lấy được quả cầu ghi số 7 hoặc 8” là $\frac{1}{4}$ .

Bài 8.12 trang 45 SBT Toán 7 Tập 2: Một hộp đựng 14 quả cầu được đánh các số 10; 11; …; 23. Lẫy ngẫu nhiên một quả cầu trong hộp. Tính xác suất để:

a) Quả cầu lấy được ghi số 24;

b) Quả cầu lấy được ghi số lẻ;

c) Quả cầu lấy được ghi số 11;

d) Quả cầu lấy được mang số 12 hoặc 13.

Lời giải:

a) Hộp đựng 14 quả cầu được đánh các số 10; 11; …; 23 nên không có quả cầu nào đánh số 24.

Do đó biến cố “Quả cầu lấy được ghi số 24” là biến cố không thể.

Vậy xác suất biến cố đã cho bằng 0.

b) Biến cố “Quả cầu lấy được ghi số chẵn” và biến cố “Quả cầu lấy được ghi số lẻ” là đồng khả năng.

Vậy xác suất của biến cố cần tìm là $\frac{1}{2}$ .

c) Mỗi quả cầu có khả năng lấy được như nhau. Có 14 biến cố đồng khả năng. Vậy xác suất của biến cố đang xét là $\frac{1}{14}$ .

d) Xét 7 biến cố sau:

A: “Quả cầu lấy được mang số 10 hoặc 11”;

B: “Quả cầu lấy được mang số 12 hoặc 13”;

C: “Quả cầu lấy được mang số 14 hoặc 15”;

D: “Quả cầu lấy được mang số 16 hoặc 17”;

E: “Quả cầu lấy được mang số 18 hoặc 19”;

F: “Quả cầu lấy được mang số 20 hoặc 21”;

G: “Quả cầu lấy được mang số 22 hoặc 23”;

Biến cố A xảy ra khi lấy được quả cầu mang số 10 và 11.

Biến cố B xảy ra khi lấy được quả cầu mang số 12 và 13.

Biến cố C xảy ra khi lấy được quả cầu mang số 14 và 15.

Biến cố D xảy ra khi lấy được quả cầu mang số 16 và 17.

Biến cố E xảy ra khi lấy được quả cầu mang số 18 và 19.

Biến cố F xảy ra khi lấy được quả cầu mang số 20 và 21.

Biến cố G xảy ra khi lấy được quả cầu mang số 22 và 23.

Do lấy ngẫu nhiên nên mỗi quả cầu có khả năng rút được như nhau.

Do đó bảy biến cố A, B, C, D, E, F, G là đồng khả năng. Vì luôn xảy ra duy nhất một trong bảy biến cố này nên xác suất của biến cố B đang xét là $\frac{1}{7}$ .

Vậy xác suất của biến cố “Quả cầu lấy được mang số 12 hoặc 13” là $\frac{1}{7}$ .

Bài 8.13 trang 45 SBT Toán 7 Tập 2: Một hộp đựng 20 quả bóng có cùng kích thước, khác nhau về màu sắc trong đó có 4 quả bóng màu xanh, 4 quả bóng màu đỏ, 4 quả bóng màu tím, 4 quả bóng màu vàng và 4 quả bóng màu trắng. Bạn Minh lấy ngẫu nhiên một quả bóng từ trong hộp.

Xét 5 biến cố sau:

A: “Minh lấy được quả bóng màu xanh”;

B: “Minh lấy được quả bóng màu đỏ”;

C: “Minh lấy được quả bóng màu tím”;

D: “Minh lấy được quả bóng màu vàng”;

E: “Minh lấy được quả bóng màu trắng”;

a) Hãy giải thích vì sao các biến cố A, B, C, D, E là đồng khả năng.

b) Tính xác suất của các biến cố A, B, C, D, E.

Lời giải:

a) Mỗi quả bóng có khả năng được chọn như nhau. Số quả bóng màu xanh, màu đỏ, màu tím, màu vàng và màu trắng bằng nhau nên các biến cố A, B, C, D, E là đồng khả năng.

b) Vì luôn xảy ra duy nhất một biến cố trong năm biến cố này nên xác suất của năm biến cố bằng nhau và bằng $\frac{1}{5}$ .

Giải SBT Toán 7 trang 46 Tập 2

Bài 8.14 trang 46 SBT Toán 7 Tập 2: Một thùng kín có 40 quả bóng cùng kích thước, một số quả có màu trắng và một số quả có màu đen. Sơn lấy ngẫu nhiên một quả bóng trong thùng. Biết rằng biến cố “Sơn chọn được quả bóng màu trắng” và biến cố “Sơn chọn được quả bóng màu đen” là đồng khả năng. Hỏi trong thùng chứa bao nhiêu quả bóng màu trắng.

Lời giải:

Biến cố “Sơn chọn được quả bóng màu trắng” và biến cố “Sơn chọn được quả bóng màu đen” là đồng khả năng . Do đó, số quả bóng màu trắng bằng số quả bóng màu đen. Vậy trong thùng chứa 20 quả bóng màu trắng.

Bài 8.15 trang 46 SBT Toán 7 Tập 2: Một chuyến xe khách có 28 hành khách nam và 31 hành khách nữ. Đến một bến xe có một số hành khách nữ xuống xe. Chọn ngẫu nhiên một hành khách còn lại trên xe. Biết rằng xác suất để chọn được hành khách nữ là $\frac{1}{2}$ . Hỏi có bao nhiêu hành khách nữ đã xuống xe?

Lời giải:

Gọi n (người) là số hành khách nữ xuống xe (n $\in$ ℕ*) . Khi đó, trên xe còn 31 – n hành khách nữ và 28 hành khách nam.

Xác suất để chọn được hành khách nữ là $\frac{1}{2}$ nên số hành khách nữ còn lại trên xe bằng số hành khách nam. Do đó, 31 – n = 28

Suy ra n = 3.

Vậy số hành khách nữ đã xuống xe là 3 người.

Bài 8.16 trang 46 SBT Toán 7 Tập 2: Một chiếc hộp chứa 50 viên bi cùng kích thước gồm một số viên bi màu xanh; một số viên bi màu đỏ; một số viên bi màu trắng; một số viên bi màu tím và một số viên bi màu vàng. Bạn Bình lấy ngẫu nhiên một viên bi trong hộp. Biết rằng 5 biến cố sau đây là đồng khả năng:

A: “Bình lấy được viên bi màu xanh”;

B: “Bình lấy được viên bi màu đỏ”;

C: “Bình lấy được viên bi màu trắng”;

D: “Bình lấy được viên bi màu tím”;

E: “Bình lấy được viên bi màu vàng”;

Hỏi trong hộp chứa bao nhiêu viên bi mỗi loại?

Lời giải:

Do lấy ngẫu nhiên nên mỗi viên bi có khả năng được lấy như nhau.

Do đó số viên bi màu xanh, số viên bi màu đỏ, số viên bi màu trắng, số viên bi màu tím và số viên bi màu vàng bằng nhau.

Vậy trong hộp mỗi loại có 10 viên bi.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

SBT Toán 7 Bài 30: Làm quen với xác suất của biến cố

SBT Toán 7 Ôn tập chương 8

Câu hỏi:

Trả lời:

Bài liên quan:

Leave a Comment Hủy