Bài trang sách bài tập Toán lớp 6 Tập 2: Một loại cà phê hòa tan có chứa 40% cà phê tinh chất. Tính khối lượng cà phê tinh chất trong một hộp có chứa 200 g cà phê hòa tan đó.

Câu hỏi:

Bài trang sách bài tập Toán lớp 6 Tập 2: Một loại cà phê hòa tan có chứa 40% cà phê tinh chất. Tính khối lượng cà phê tinh chất trong một hộp có chứa 200 g cà phê hòa tan đó.

Trả lời:

Lời giải:
Bài toán đưa về tìm a, biết a bằng 40% của 200.
Khối lượng cà phê tinh chất trong một hộp có chứa 200 g cà phê hòa tan đó là:
200 . 40% = 80 (g)
Vậy khối lượng cà phê tinh chất trong một hộp có chứa 200 g cà phê hòa tan đó là 80 g.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Giải SGK Toán 7 (Cánh diều): Bài tập cuối chương 6

   Giải bài tập Toán lớp 7 Bài tập cuối chương 6

   Giải Toán 7 trang 68 Tập 2

   Bài 1 trang 68 Toán 7 Tập 2: Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó.

   a) -7x + 5.

   b) 2 021×2 – 2 022x + 2 023.

   c) 2y3 – $\frac{3}{y+2}$ + 4.

   d) -2tm + 8t2 + t – 1, với m là số tự nhiên lớn hơn 2.

   Lời giải:

   a) Biểu thức -7x + 5 là đa thức một biến x, đa thức này có bậc bằng 1.

   b) Biểu thức 2 021×2 – 2 022x + 2 023 là đa thức một biến x, đa thức này có bậc bằng 2.

   c) Biểu thức 2y3 – $\frac{3}{y+2}$ + 4 không phải đa thức do có chứa biến ở dưới mẫu.

   d) Biểu thức -2tm + 8t2 + t – 1 là đa thức một biến t, đa thức này có bậc bằng m, với m là số tự nhiên lớn hơn 2.

   Bài 2 trang 68 Toán 7 Tập 2: Tính giá trị của biểu thức:

   a) A = -5a – b – 20 tại a = -4, b = 18;

   b) B = -8xyz + 2xy + 16y tại x = -1, y = 3, z = -2;

   c) C = -x2021y2 + 9×2021 tại x = -1, y = -3.

   Lời giải:

   a) Thay a = -4, b = 18 vào biểu thức A = -5a – b – 20 ta được:

   A = -5.(-4) – 18 – 20

   A = 20 – 18 – 20

   A = -18.

   Vậy A = -18 khi a = -4, b = 18.

   b) Thay x = -1, y = 3, z = -2 vào biểu thức B = -8xyz + 2xy + 16y ta được:

   B = -8.(-1).3.(-2) + 2.(-1).3 + 16.3

   B = -48 + (-6) + 48

   B = -6.

   Vậy B = -6 khi x = -1, y = 3, z = -2.

   c) Thay x = -1, y = -3 vào biểu thức C = -x2021y2 + 9×2021 ta được:

   C = – (-1)2021 .(-3)2 + 9.(-1)2021 

   C = -(-1) . 9 + 9 . (-1)

   C = 1.9 + (‒9)

   C = 9 + (-9)

   C = 0.

   Vậy C = 9 khi x = -1, y = -3.

   Bài 3 trang 68 Toán 7 Tập 2: Viết đa thức trong mỗi trường hợp sau:

   a) Đa thức bậc nhất có hệ số của biến bằng -2 và hệ số tự do bằng 6;

   b) Đa thức bậc hai có hệ số tự do bằng 4;

   c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0;

   d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0.

   Lời giải:

   a) Đa thức cần tìm là đa thức bậc nhất nên số mũ cao nhất của biến là 1.

   Đa thức có hệ số của biến bằng -2 và hệ số tự do bằng 6 nên đa thức bậc nhất cần tìm là: -2x + 6.

   b) Đa thức cần tìm là đa thức bậc hai nên số mũ cao nhất của biến là 2 và hệ số của luỹ thừa bậc 2 của biến là một số tuỳ ý khác 0.

   Đa thức có hệ số của luỹ thừa bậc 1 của biến là một số tùy ý (do đề bài không đề cập đến) và hệ số tự do bằng 4.

   Khi đó đa thức cần tìm có dạng ax2 + bx + 4 với a, b ∈ ℝ và a ≠ 0.

   Chẳng hạn, ta có đa thức cần tìm có thể là x2 + x + 4; 2×2 + 4;…

   c) Đa thức cần tìm là đa thức bậc bốn nên số mũ cao nhất của biến là 4 và hệ số của luỹ thừa bậc 4 của biến là một số tuỳ ý khác 0.

   Đa thức có hệ số của lũy thừa bậc 3 của biến bằng 0 và hệ số của lũy thừa bậc 2, bậc 1 của biến là một số tùy ý, hệ số tự do là một số tùy ý.

   Khi đó đa thức cần tìm có dạng ax4 + bx2 + cx + d với a, b, c, d ∈ ℝ và a ≠ 0.

   Chắng hạn, ta có đa thức cần tìm có thể là: x4; x4 + 2×2 + 3x + 4;…

   d) Đa thức cần tìm là đa thức bậc sáu nên số mũ cao nhất của biến là 6 và hệ số của luỹ thừa bậc 6 là một số tùy ý khác 0.

   Trong đa thức này tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0 và hệ số các lũy thừa bậc chẵn còn lại của đa thức là một số tùy ý, hệ số tự do là một số tùy ý.

   Khi đó đa thức cần tìm có dạng ax6 + bx4 + cx2 + d với a, b, c, d ∈ ℝ và a ≠ 0.

   Chẳng hạn, ta có đa thức cần tìm có thể là 2×6 + 3; x6 + 2×2;…

   Bài 4 trang 68 Toán 7 Tập 2: Kiểm tra xem trong các số -1, 0, 1, 2, số nào là nghiệm của mỗi đa thức sau:

   a) 3x – 6;

   b) x4 – 1;

   c) 3×2 – 4x;

   d) x2 + 9.

   Lời giải:

   a) Ta thay lần lượt các giá trị x = -1, x = 0, x = 1, x = 2 vào đa thức 3x – 6 để kiểm tra số nào là nghiệm của đa thức đó.

   + Thay x = -1 vào đa thức ta được: 3.(-1) – 6 = -3 – 6 = -9 ≠ 0.

   Do đó số -1 không là nghiệm của đa thức 3x – 6.

   + Thay x = 0 vào đa thức ta được: 3.0 – 6 = 0 – 6 = -6 ≠ 0.

   Do đó số 0 không là nghiệm của đa thức 3x – 6.

   + Thay x = 1 vào đa thức ta được: 3.1 – 6 = 3 – 6 = -3 ≠ 0.

   Do đó số 1 không là nghiệm của đa thức 3x – 6.

   + Thay x = 2 vào đa thức ta được: 3.2 – 6 = 6 – 6 = 0.

   Do đó số 2 là nghiệm của đa thức 3x – 6.

   Vậy trong các số -1, 0, 1, 2 thì số 2 là nghiệm của đa thức 3x – 6.

   b) Ta thay lần lượt các giá trị x = -1, x = 0, x = 1, x = 2 vào đa thức x4 – 1 để kiểm tra số nào là nghiệm của đa thức đó.

   + Thay x = -1 vào đa thức x4 – 1 ta được: (-1)4 – 1 = 1 – 1 = 0.

   Do đó số -1 là nghiệm của đa thức x4 – 1.

   + Thay x = 0 vào đa thức x4 – 1 ta có: 04 – 1 = -1 ≠ 0.

   Do đó số 0 không là nghiệm của đa thức x4 – 1.

   + Thay x = 1 vào đa thức x4 – 1 ta có: 14 – 1 = 0.

   Do đó số 1 là nghiệm của đa thức x4 – 1.

   + Thay x = 2 vào đa thức x4 – 1 ta có: 24 – 1 = 16 – 1 = 15 ≠ 0.

   Do đó số 2 không là nghiệm của đa thức x4 – 1.

   Vậy trong các số -1, 0, 1, 2 thì số – 1 và số 1 là nghiệm của đa thức x4 – 1.

   c) Ta thay lần lượt các giá trị x = -1, x = 0, x = 1, x = 2 vào đa thức 3×2 – 4x để kiểm tra số nào là nghiệm của đa thức đó.

   + Thay x = -1 vào đa thức trên ta được: 3.(-1)2 – 4.(-1) = 3 + 4 = 7 ≠ 0.

   Do đó số -1 không là nghiệm của đa thức 3×2 – 4x.

   + Thay x = 0 vào đa thức trên ta được : 3.02 – 4.0 = 0.

   Do đó số 0 là nghiệm của đa thức 3×2 – 4x.

   + Thay x = 1 vào đa thức trên ta có: 3.12 – 4.1 = 3 – 4 = -1 ≠ 0.

   Do đó số 1 không là nghiệm của đa thức 3×2 – 4x.

   + Thay x = 2 vào đa thức trên ta có: 3 . 22 – 4 . 2 = 12 – 8 = 4 ≠ 0.

   Do đó số 2 không là nghiệm của đa thức x4 – 1 .

   Vậy trong các số -1, 0, 1, 2 thì số 0 là nghiệm của đa thức 3×2 – 4x.

   d) Ta thay lần lượt các giá trị x = -1, x = 0, x = 1, x = 2 vào đa thức x2 + 9 để kiểm tra số nào là nghiệm của đa thức đó.

   + Thay x = -1 vào đa thức trên ta có: (-1)2 + 9 = 10 ≠ 0.

   Do đó số -1 không là nghiệm của đa thức x2 + 9.

   + Thay x = 0 vào đa thức trên ta có: 02+ 9 = 9 ≠ 0.

   Do đó số 0 không là nghiệm của đa thức x2 + 9.

   + Thay x = 1 vào đa thức trên ta có: 12 + 9 = 10 ≠ 0.

   Do đó số 1 không là nghiệm của đa thức x2 + 9.

   + Thay x = 2 vào đa thức trên ta có: 22 + 9 = 13 ≠ 0.

   Do đó số 2 không là nghiệm của đa thức x2 + 9.

   Vậy trong các số -1, 0, 1, 2 thì không có số nào là nghiệm của đa thức x2 + 9.

   Bài 5 trang 68 Toán 7 Tập 2: Cho đa thức P(x) = -9×6 + 4x + 3×5 + 5x + 9×6- 1.

   a) Thu gọn đa thức P(x).

   b) Tìm bậc của đa thức P(x).

   c) Tính giá trị của đa thức P(x) tại x = -1; x = 0; x = 1.

   Lời giải:

   a) Thu gọn đa thức P(x):

   P(x) = -9×6 + 4x + 3×5 + 5x + 9×6 – 1

   P(x) = (-9×6 + 9×6) + 3×5 + (4x + 5x) – 1

   P(x) = 3×5 + 9x – 1.

   b) Đa thức P(x) có số mũ cao nhất của biến là 5 nên bậc của đa thức P(x) bằng 5.

   c) Với P(x) = 3×5 + 9x – 1:

   + Thay x = ‒1 vào đa thức ta có:

   P(-1) = 3.(-1)5 + 9.(-1) – 1 = 3.(-1) + (-9) – 1 = -3 – 9 – 1 = -13.

   + Thay x = 0 vào đa thức ta có:

   P(0) = 3.05 + 9.0 – 1 = 0 + 0 -1 = -1.

   + Thay x = 1 vào đa thức ta có:

   P(1) = 3.15 + 9.1 – 1 = 3 + 9 – 1 = 11.

   Vậy P(-1) = -13; P(0) = -1 và P(1) = 11.

   Bài 6 trang 68 Toán 7 Tập 2: Tính:

   a) -2×2 + 6×2;

   b) 4×3 – 8×3;

   c) 3×4(-6×2);

   d) (-24×6) : (-4×3).

   Lời giải:

   a) -2×2 + 6×2 = (-2 + 6).x2 = 4×2.

   b) 4×3 – 8×3 = (4 – 8).x3 = -4×3.

   c) 3×4(-6×2) = 3.(-6).x4.x2 = -18×4+2 = -18×6.

   d) (-24×6) : (-4×3) = [-24 : (-4)].(x6 : x3) = 6×6-3 = 6×3.

   Bài 7 trang 68 Toán 7 Tập 2: Tính:

   a) (x2 + 2x + 3) + (3×2 – 5x + 1);

   b) (4×3 – 2×2 – 6) – (x3 – 7×2 + x – 5);

   c) -3×2(6×2 – 8x + 1);

   d) (4×2 + 2x + 1)(2x – 1);

   e) (x6 – 2×4 + x2) : (-2×2);

   g) (x5 – x4 – 2×3) : (x2 + x).

   Lời giải:

   a) (x2 + 2x + 3) + (3×2 – 5x + 1)

   = x2 + 2x + 3 + 3×2 – 5x + 1

   = (x2 + 3×2) + (2x – 5x) + (3 + 1)

   = (1 + 3)x2 + (2 – 5)x + 4

   = 4×2 – 3x + 4.

   b) (4×3 – 2×2 – 6) – (x3 – 7×2 + x – 5)

   = 4×3 – 2×2 – 6 – x3 + 7×2 – x + 5

   = (4×3 – x3) + (-2×2 + 7×2) – x + (-6 + 5)

   = (4 – 1)x3 + (‒2 + 7)x2 – x ‒ 1

   = 3×3 + 5×2 – x – 1.

   c) -3×2(6×2 – 8x + 1)

   = -3×2.6×2 – (-3×2).8x + (-3×2).1

   = (-3).6.x2+2 – (–3).8.x2+1 + (–3).1.x2

   = -18×4 – (-24)x3 + (-3)x2

   = – 18×4 + 24×3 – 3×2.

   d) (4×2 + 2x + 1)(2x – 1)

   = 4×2.2x – 4×2.1 + 2x.2x – 2x.1 + 1.2x – 1.1

   = 4.2.x2+1 – 4.1.x2 + 2.2.x1+1 – 2x + 2x – 1

   = 8×3 – 4×2 + 4×2 + (-2x + 2x) – 1

   = 8×3 + (-4×2 + 4×2) – 1

   = 8×3 – 1.

   e) (x6 – 2×4 + x2) : (-2×2)

   = x6 : (-2×2) – 2×4 : (-2×2) + x2 : (-2×2)

   = $\frac{1}{-2}{x}^{6-2}-\frac{2}{-2}{x}^{4-2}+\frac{1}{-2}{x}^{2-2}$

   = $\frac{-1}{2}{x}^4+x^2-\frac{1}{2}{x}^0$

   $=\frac{-1}{2}{x}^4+x^2-\frac{1}{2}$

   g) Thực hiện phép chia đa thức ta được:

   

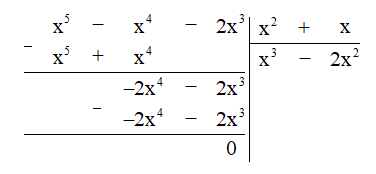
   Vậy (x5 – x4 – 2×3) : (x2 + x) = x3 – 2×2.

   Giải Toán 7 trang 69 Tập 2

   Bài 8 trang 69 Toán 7 Tập 2: Cho hai đa thức: A(x) = 4×4 + 6×2 – 7×3 – 5x – 6 và B(x) = -5×2 + 7×3 + 5x + 4 – 4×4.

   a) Tìm đa thức M(x) sao cho M(x) = A(x) + B(x).

   b) Tìm đa thức C(x) sao cho A(x) = B(x) + C(x).

   Lời giải:

   a) M(x) = A(x) + B(x)

   = (4×4 + 6×2 – 7×3 – 5x – 6) + (-5×2 + 7×3 + 5x + 4 – 4×4)

   = 4×4 + 6×2 – 7×3 – 5x – 6 – 5×2 + 7×3 + 5x + 4 – 4×4

   = (4×4 – 4×4) + (-7×3 + 7×3) + (6×2 – 5×2) + (-5x + 5x) + (-6 + 4)

   = 0.x4 + 0.x3 + (6 – 5).x2 + 0.x + (‒2)

   = x2 – 2.

   Vậy M(x) = x2 – 2.

   b) Ta có: A(x) = B(x) + C(x)

   Suy ra C(x) = A(x) – B(x)

   = (4×4 + 6×2 – 7×3 – 5x – 6) – (-5×2 + 7×3 + 5x + 4 – 4×4)

   = 4×4 + 6×2 – 7×3 – 5x – 6 + 5×2 – 7×3 – 5x – 4 + 4×4

   = (4×4 + 4×4) + (-7×3 – 7×3) + (6×2 + 5×2) + (-5x – 5x) + (-6 – 4)

   = (4 + 4).x4 + (-7 – 7).x3 + (6 + 5).x2 + (-5 – 5).x + (-10)

   = 8×4 – 14×3 + 11×2 – 10x – 10.

   Vậy C(x) = 8×4 – 14×3 + 11×2 – 10x – 10.

   Bài 9 trang 69 Toán 7 Tập 2: Cho P(x) = x3 + x2 + x + 1 và Q(x) = x4 – 1. Tìm đa thức A(x) sao cho P(x).A(x) = Q(x).

   Lời giải:

   Ta có: P(x).A(x) = Q(x)

   Suy ra A(x) = Q(x) : P(x).

   Thực hiện phép chia đa thức ta được:

   

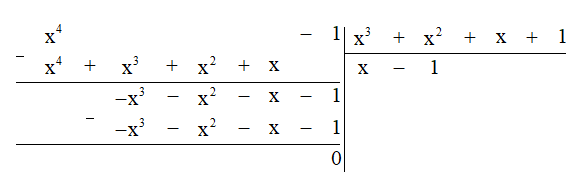
   Do đó Q(x) : P(x) = x – 1

   Vậy A(x) = x – 1.

   Bài 10 trang 69 Toán 7 Tập 2: Nhân dịp lễ Giáng sinh, một cửa hàng bán quần áo trẻ em thông báo khi mua mỗi bộ quần áo sẽ được giảm giá 30% so với giá niêm yết. Giả sử giá niêm yết một bộ quần áo là x (đồng). Viết biểu thức tính số tiền phải trả khi mua loại quần áo đó với số lượng:

   a) 1 bộ;

   b) 3 bộ;

   c) y bộ.

   Lời giải:

   Do mỗi bộ quần áo được giảm giá 30% so với giá niêm yết (x đồng) nên giá sau khi đã giảm sẽ bằng 100% – 30% = 70% giá niêm yết.

   Vậy ta có giá một bộ quần áo sau khi giảm 30% là: 70% . x = 0,7.x (đồng).

   a) Số tiền phải trả khi mua 1 bộ là: 0,7x.1 = 0,7x (đồng).

   Vậy biểu thức tính số tiền khi mua 1 bộ loại quần áo đó là 0,7x đồng.

   b) Số tiền phải trả khi mua 3 bộ là: 0,7x.3 = 2,1x (đồng).

   Vậy biểu thức tính số tiền khi mua 3 bộ loại quần áo đó là 2,1x đồng.

   c) Số tiền phải trả khu mua y bộ là: 0,7xy (đồng).

   Vậy biểu thức tính số tiền khi mua y bộ loại quần áo đó là 0,7xy đồng.

   Bài 11 trang 69 Toán 7 Tập 2: Một doanh nghiệp kinh doanh cà phê cho biết: Sau khi rang xong, khối lượng cà phê giảm 12% so với trước khi rang.

   a) Tìm số thích hợp cho $?$ ở bảng sau:

    

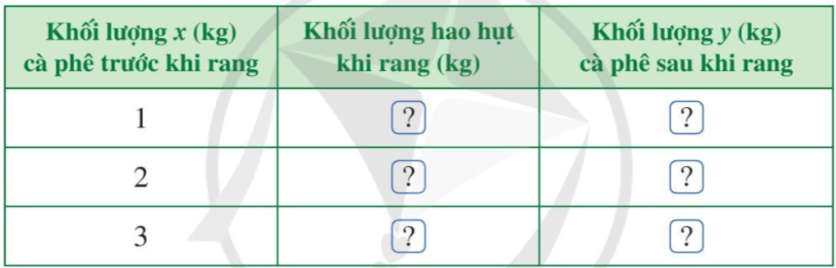
   b) Tìm công thức chỉ mối liên hệ giữa x và y.

   c) Để có được 2 tấn cà phê sau khi rang thì doanh nghiệp đó cần sử dụng bao nhiêu tấn cà phê trước khi rang?

   Lời giải:

   a) – Khối lượng cà phê trước khi rang là 1 kg thì:

    + Khối lượng hao hụt khi rang là: 1.12% = 0,12 kg;

   + Khối lượng cà phê sau khi rang là: 1 – 0,12 = 0,88 kg.

   – Khối lượng cà phê trước khi rang là 2 kg thì:

   + Khối lượng hao hụt khi rang là: 2.12% = 0,24 kg;

   + Khối lượng cà phê sau khi rang là: 2 – 0,24 = 1,76 kg.

   – Khối lượng cà phê trước khi rang là 3 kg thì:

   + Khối lượng hao hụt khi rang là: 3.12% = 0,36 kg;

   + Khối lượng cà phê sau khi rang là: 3 – 0,36 = 2,64 kg.

   Ta có bảng sau:

   Khối lượng x (kg) cà phê trước khi rang	Khối lượng hao hụt khi rang (kg)	Khối lượng y (kg) cà phê sau khi rang
   1	0,12	0,88
   2	0,24	1,76
   3	0,36	2,64

   b) Sau khi rang xong, khối lượng cà phê giảm 12% so với trước khi rang nên khối lượng cà phê sau khi rang bằng 100% – 12% = 88% khối lượng cà phê lúc đầu.

   Do đó: y = 88%x = 0,88x.

   Vậy công thức chỉ mối liên hệ giữa x và y là: y = 0,88x.

   c) Số tấn cà phê cần dùng để có được 2 tấn cà phê sau khi rang là:

   2 : 88% = 2 : $\frac{88}{100}$ = 2 . $\frac{100}{88}$ = $\frac{25}{11}$ ≈ 2,27 tấn.

   Vậy doanh nghiệp đó cần sử dụng khoảng 2,27 tấn cà phê trước khi rang để thu được 2 tấn cà phê sau khi rang.

   Bài 12 trang 69 Toán 7 Tập 2: Một công ty sau khi tăng giá 50 nghìn đồng mỗi sản phẩm so với giá ban đầu là x (nghìn đồng) với x < 60 thì có doanh thu là -5×2 + 50x + 15 000 (nghìn đồng). Tính số sản phẩm mà công ty đã bán được theo x.

   Lời giải:

   Sau khi tăng giá 50 nghìn đồng mỗi sản phẩm so với giá ban đầu là x (nghìn đồng) (x < 60) thì giá của mỗi sản phẩm sau khi tăng giá là x + 50 (nghìn đồng).

   Khi đó số sản phẩm đã bán được là: (-5×2 + 50x + 15 000) : (x + 50)

   Thực hiện phép chia đa thức ta được:

   

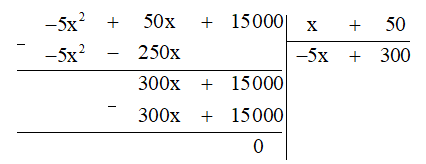
   Do đó (-5×2 + 50x + 15 000) : (x + 50) = ‒5x + 300

   Vậy công ty đã bán được -5x + 300 sản phẩm với x < 60.

   Bài 13 trang 69 Toán 7 Tập 2: Một công ty du lịch dự định dùng 2 xe ô tô để chở khách đi tham quan, mỗi xe chở tối đa 35 khách, mức giá cho chuyến đi là 900 nghìn/người và đã có 50 người đăng kí tham quan. Công ty đặt chính sách khuyến mãi như sau: Sẽ giảm giá cho mỗi người trong đoàn tham quan là 10 nghìn đồng khi cứ có thêm 1 khách tham quan ngoài 50 khách trên.

   a) Giả sử số khách tham quan thêm là x (x ≤ 20). Tính số tiền mà công ty thu được theo x.

   b) Nếu 2 xe ô tô của công ty đều chở tối đa số khách thì số tiền công ty thu được tổng cộng là bao nhiêu?

   Lời giải:

   a) Số tiền giảm giá cho mỗi người khi có thêm x khách tham quan là: 10x (nghìn đồng).

   Khi đó số tiền mỗi người cần trả khi được giảm giá là: 900 – 10x (nghìn đồng).

   Ban đầu có 50 khách, có thêm x khách thì tổng số khách tham quan là x + 50 (khách).

   Số tiền công ty thu được là (x + 50)(900 – 10x) (nghìn đồng).

   b) Mỗi xe được chở tối đa 35 khách nên nếu cả 2 xe ô tô đều chở tối đa khách thì tổng số khách tham quan là: 2.35 = 70 (khách).

   Khi đó có thêm 20 khách so với 50 khách ban đầu.

   Tức là ta có x = 20.

   Thay x = 20 vào biểu thức (x + 50)(900 – 10x) ta có số tiền công ty thu được là:

   (20 + 50). (900 – 10.20) = 70.(900 – 200) = 70.700 = 49 000 (nghìn đồng) = 49 triệu đồng.

   Vậy công ty thu được tổng cộng là 49 triệu đồng.

   Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:

   Giải SGK Toán 7 Bài 4: Phép nhân đa thức một biến

   Giải SGK Toán 7: Bài tập cuối chương 6

   Giải SGK Toán 7 Bài 1: Tổng các góc của một tam giác

   Giải SGK Toán 7 Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

   Giải SGK Toán 7 Bài 3: Hai tam giác bằng nhau

2. Giải SGK Toán 7 (Chân trời sáng tạo) Bài tập cuối chương 6

   Giải bài tập Toán lớp 7 Bài tập cuối chương 6

   Giải Toán 7 trang 23 Tập 2

   Bài 1 trang 23 Toán lớp 7: Tìm x,y,z biết:

   a) $\frac{x}{3}=\frac{y}{8}=\frac{z}{5}$ và x + y – z = 30

   b) $\frac{x}{10}=\frac{y}{5}$;$\frac{y}{2}=\frac{z}{3}$ và x + 4z = 320

   Phương pháp giải:

   Sử dụng tính chất của dãy tỉ số bằng nhau: $\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=\frac{x\pm y\pm z}{a\pm b\pm c}$

   Lời giải:

   a) Vì đề bài cho $\frac{x}{3}=\frac{y}{8}=\frac{z}{5}$ mà x + y – z = 30 nên áp dụng tính chất của dãy tỉ số bằng nhau$\Rightarrow \frac{x}{3}=\frac{y}{8}=\frac{z}{5}=\frac{x+y-z}{3+8-5}=\frac{30}{6}=5$

   $\Rightarrow \frac{x}{3}=5\Rightarrow x=15$;

   $\frac{y}{8}=5$$\Rightarrow y=40$;

   $\frac{z}{5}=5\Rightarrow z=25$

   Vậy x = 15, y = 40, z = 25.

   b)      Ta có :

   $\Rightarrow \frac{x}{10}=\frac{y}{5}\Rightarrow 5x=10y\Rightarrow y=\frac{x}{2}$

   Tương tự $\Rightarrow \frac{y}{2}=\frac{z}{3}\Rightarrow 3y=2z\Rightarrow y=\frac{2z}{3}$

   $\Rightarrow \frac{x}{2}=\frac{2z}{3}$

   Áp dụng tính chất của dãy tỉ số bằng nhau

   $\Rightarrow \frac{x}{2}=\frac{4z}{6}=\frac{x+4z}{8}=40$

   $\Rightarrow \frac{x}{2}=40\Rightarrow x=80$;

   $\frac{4z}{6}=40\Rightarrow z=60$

   Thay $x=80$ vào $\frac{x}{10}=\frac{y}{5}\Rightarrow \frac{80}{10}=\frac{y}{5}\Rightarrow 400=10y\Rightarrow y=40$

   Vậy x = 80, y = 40, z = 60.

   Bài 2 trang 23 Toán lớp 7: Hai bạn Mai và Hoa đi xe đạp từ trường đến nhà thi đấu để học bơi. Vận tốc của Mai kém vận tốc của Hoa là 3 km/h. Thời gian Mai và Hoa đi từ trường đến nhà thi đấu lần lượt là 30 phút, $\frac{2}{5}$ giờ. Hỏi quãng đường từ trường đến nhà thi đấu dài bao nhiêu kilômét?

   Phương pháp giải:

   Vận tốc và thời gian đi cùng một quãng đường là hai đại lượng tỉ lệ nghịch

   Lời giải:

   Gọi vận tốc của Mai là x, vận tốc của Hoa là y (km/h) (x,y > 0)

   Thời gian Mai và Hoa lần lượt là là 30 phút = $\frac{1}{2}$ giờ và $\frac{2}{5}$ giờ

   Vì quãng đường là như nhau vận tốc và thời gian đi là hai đại lượng tỉ lệ nghịch. 

   Áp dụng tính chất của hai đại lượng tỉ lệ nghịch, ta có:

   $\frac{1}{2}x=\frac{2}{5}y\Rightarrow \frac{x}{2}=\frac{2y}{5}\Rightarrow 5x=4y$ (1)

   Mà theo đề bài vận tốc của Mai kém hơn vận tốc của Hoa là 3km/h nên ta có: $y–x=3\Rightarrow y=3+x$

   Thay y = 3 + x vào (1) ta có :

   5x = 4 . ( 3 + x )

   $\Rightarrow 5x=12+4x\Rightarrow x=12$

   Vì vận tốc của Mai là 12 km/h nên quãng đường từ trường đến nhà thi đấu sẽ là  :

   12 . $\frac{1}{2}$ = 6 km

   Bài 3 trang 23 Toán lớp 7: Số quyển sách của ba bạn An, Bình và Cam tỉ lệ với các số 3; 4; 5. Hỏi mỗi bạn có bao nhiêu quyển sách? Biết rằng số quyển sách của Bình ít hơn tổng số quyển sách của An và Cam là 8 quyển sách.

   Phương pháp giải:

   • Áp dụng tính chất của dãy tỉ số bằng nhau $\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=\frac{x\pm y\pm z}{a\pm b\pm c}$

   Lời giải:

   Gọi số sách của An là x, số sách của Bình là y và số sách của Cam là z (x,y,z > 0)

   Theo đề bài số sách của 3 bạn lần lượt tỉ lệ với 3. 4. 5 nên ta có:

   $\frac{x}{3}=\frac{y}{4}=\frac{z}{5}$

   Mà số sách của Bình ít hơn số sách của An và Cam là 8 quyển nên ta có : x – y + z = 8.

   Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

   $\Rightarrow \frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x-y+z}{4}=2$

   $\Rightarrow \frac{x}{3}=2\Rightarrow x=6;\frac{y}{4}=2\Rightarrow y=8;\frac{z}{5}=2\Rightarrow z=10$

   Vậy số sách của An, Bình và Cam lần lượt là 6, 8, 10 quyển

   Bài 4 trang 23 Toán lớp 7: a) Tìm ba số x,y,z thỏa mãn x : y : z = 2 : 3 : 5 và x + y + z = 30     

   b) Tìm ba số a,b,c thỏa mãn a : b : c = 6 : 8 : 10 và a – b + c = 16

   Phương pháp giải:

   Áp dụng tính chất của dãy tỉ số bằng nhau $\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=\frac{x\pm y\pm z}{a\pm b\pm c}$

   Lời giải:

   a) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

   $\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{x+y+z}{10}=\frac{30}{10}=3$

   $\Rightarrow \frac{x}{2}=3\Rightarrow x=6;\frac{y}{3}=3\Rightarrow y=9;\frac{z}{5}=3\Rightarrow z=15$

   Vậy $x=6;y=9;z=15$

   b) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :

   $\frac{a}{6}=\frac{b}{8}=\frac{c}{10}=\frac{a-b+c}{8}=\frac{16}{8}=2$

   $\Rightarrow \frac{a}{6}=2\Rightarrow a=12;\frac{b}{8}=2\Rightarrow b=16;\frac{c}{10}=2\Rightarrow c=20$

   Vậy $a=12;b=16;c=20$

   Bài 5 trang 23 Toán lớp 7: Tổng số học sinh của hai lớp 7A và 7B là 55 học sinh. Tìm số học sinh của mỗi lớp biết rằng số học sinh lớp 7A bằng $\frac{5}{6}$ số học sinh lớp 7B.

   Phương pháp giải:

   • Ta lập tỉ số giữa học sinh của 2 lớp rồi áp dụng tính chất của dãy tỉ số bằng nhau.
   • Sau đó tính được số học sinh của mỗi lớp

   Lời giải:

   Gọi số học sinh lớp 7A là x, số học sinh lớp 7B là y ( $x,y\in N^{\ast }$)

   Vì theo đề bài 2 lớp có tổng số học sinh là 55 nên ta có : x + y = 55

   Vì số học sinh lớp 7A bằng $\frac{5}{6}$ số học sinh lớp 7B nên ta có : $x=\frac{5}{6}y\Rightarrow \frac{x}{y}=\frac{5}{6}\Rightarrow \frac{x}{5}=\frac{y}{6}$

   Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

   $\Rightarrow \frac{x}{5}=\frac{y}{6}=\frac{x+y}{11}=\frac{55}{11}=5$

   $\Rightarrow \frac{x}{5}=5\Rightarrow x=25;\frac{y}{6}=5\Rightarrow y=30$

   Vậy lớp 7A có 25 học sinh, lớp 7B có 30 học sinh.

   Bài 6 trang 23 Toán lớp 7: Linh và Nam thi nhau giải toán ôn tập cuối học kì. Kết quả là Linh làm được nhiều hơn Nam 3 bài và số bài Nam làm được chỉ bằng $\frac{2}{3}$số bài của Linh làm được. Hãy tìm số bài mỗi bạn làm được.

   Phương pháp giải:

   Áp dụng tính chất của dãy tỉ số bằng nhau :$\frac{a}{b}=\frac{c}{d}=\frac{a-c}{b-d}$

   Lời giải:

   Cách 1:

   Gọi số bài của Nam làm được là x và của Linh là y ( x, y > 0)

   Theo đề bài Linh làm được nhiều hơn Nam 3 bài nên ta có : y – x = 3

   Và do Nam làm được số bài bằng $\frac{2}{3}$số bài của Linh nên ta có :

   $x=\frac{2}{3}.y\Rightarrow \frac{y}{3}=\frac{x}{2}$

   Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:

   $\begin{array}{l}\frac{y}{3}=\frac{x}{2}=\frac{y-x}{3-2}=\frac{3}{1}=3\\ \Rightarrow y=3.3=9\\ x=3.2=6\end{array}$

   Vậy số bài của Nam làm được là 6 bài, của Linh làm được là 9 bài.

   Cách 2:

   Gọi số bài của Nam làm được là x và của Linh là y ( x, y > 0)

   Theo đề bài Linh làm được nhiều hơn Nam 3 bài nên ta có : y – x = 3

   Và do Nam làm được số bài bằng $\frac{2}{3}$số bài của Linh nên ta có :

   $\Rightarrow \frac{x}{y}=\frac{2}{3}$ $\Rightarrow 3x=2y$

   Do y – x = 3 nên y = 3 + x, thay vào công thức trên, ta được :

   3x = 6 + 2x $\Rightarrow$x = 6 $\Rightarrow$y = 6 + 3 = 9

   Vậy số bài của Nam làm được là 6 bài, của Linh làm được là 9 bài.

   Bài 7 trang 23 Toán lớp 7: Lớp 7A có 4 bạn làm vệ sinh xong lớp học hết 2 giờ. Hỏi nếu có 16 bạn sẽ làm vệ sinh xong lớp học trong bao lâu? (Biết rằng các bạn có năng suất làm việc như nhau)

   Phương pháp giải:

   Thời gian và số bạn làm là hai đại lượng tỉ lệ nghịch.

   Áp dụng tính chất 2 đại lượng tỉ lệ nghịch.

   Lời giải:

   Gọi thời gian để 16 bạn làm xong công việc là x ( gờ) (x > 0)

   Vì khối lượng công việc không đổi và năng suất làm việc của mỗi bạn là như nhau nên số bạn tỉ lệ nghịch với thời gian nên theo tính chất của hai đại lượng tỉ lệ nghịch, ta có:

   4.2 = 16 . x

   $\Rightarrow$ x = $\frac{8}{16}=\frac{1}{2}$

   Vậy thời gian để 16 bạn làm xong là $\frac{1}{2}$ giờ = 30 phút

   Bài 8 trang 23 Toán lớp 7: Bạn Hà muốn chia đều 1 kg đường vào n túi. Gọi p (g) là lượng đường trong mỗi túi. Hãy chứng tỏ n,p là hai đại lượng tỉ lệ nghịch và tính p theo n

   Phương pháp giải:

   Chứng minh p.n = a không đổi với a ≠ 0

   Lời giải:

   Vì bạn Hà có 1 kg đường và chia chúng vào n túi và p (g) là khối lượng đường trong mỗi túi.

   $\Rightarrow$ Số túi . số đường trong mỗi túi = số đường = 1 (kg)

   $\Rightarrow n.p=1$ với 1 ≠ 0 nên n tỉ lệ nghịch với p theo hệ số tỉ lệ là 1.

   $\Rightarrow p=\frac{1}{n}$ 

   Bài 9 trang 23 Toán lớp 7: Cho biết mỗi lít dầu ăn có khối lượng 0,8 kg.

   a) Giả sử x lít dầu ăn có khối lượng y kg. Hãy viết công thức tính y theo x.

   b) Tính thể tích của 240g dầu ăn.

   Phương pháp giải:

   +) Nếu hai đại lượng y và x liên hệ với nhau theo công thức y = k .x ( k khác 0, không đổi) thì y và x là hai đại lượng tỉ lệ thuận.

   +) Áp dụng tính chất hai đại lượng tỉ lệ thuận.

   Lời giải:

   a) Theo đề bài mỗi lít dầu ăn nặng 0,8kg nên x lít dầu ăn sẽ nặng 0,8.x (kg)

   Mà theo đề bài x kg dầu ăn có khối lượng y kg nên y = 0,8.x

   b) Đổi 0,8kg dầu ăn = 800g dầu ăn

   Gọi thể tích của 240g dầu ăn là x (lít)

   Do y và x liên hệ với nhau theo công thức y = 0,8.x nên y và x là hai đại lượng tỉ lệ thuận. Áp dụng tính chất hai đại lượng tỉ lệ thuận, ta được:

    $\frac{240}{x}=\frac{800}{1}\Rightarrow 800x=240\Rightarrow x=0,3l$

   Vậy 240g dầu ăn có thể tích là 0,3 lít

   Xem thêm các bài giải SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết:

   Bài 3: Đại lượng tỉ lệ nghịch

   Bài 1: Biểu thức số và biểu thức đại số

   Bài 2: Đa thức một biến

   Bài 3: Phép cộng và phép trừ đa thức một biến

3. Sách bài tập Toán 7 Bài tập cuối chương 6 (Chân trời sáng tạo)

   Giải SBT Toán lớp 7 Bài tập cuối chương 6

   Giải trang 17 Tập 2

   Bài 1 trang 17 Tập 2: Tìm a, b, c biết:

   a) $\frac{a}{2}=\frac{b}{1}=\frac{c}{3}$  và a + b + c = 48.

   b) $\frac{a}{2}=\frac{b}{3};\frac{b}{2}=\frac{c}{3}$  và a + c = 26.

   Lời giải:

   a) Từ $\frac{a}{2}=\frac{b}{1}=\frac{c}{3}$  và a + b + c = 48, áp dụng tính chất của dãy tỉ số bằng nhau ta có:

   $\frac{a}{2}=\frac{b}{1}=\frac{c}{3}=\frac{a+b+c}{2+1+3}=\frac{48}{6}=8.$

    

   Khi đó:

   • $\frac{a}{2}$  = 8 nên x = 8 . 2 = 16;

   • $\frac{b}{1}$  = 8 nên y = 8 . 1 = 8;

   • $\frac{c}{3}$  = 8 nên c = 8 . 3 = 24.

   Vậy a = 16, b = 8, c = 24.

   b) Ta có: $\frac{a}{2}=\frac{b}{3}$  suy ra $\frac{a}{2}:2=\frac{b}{3}:2$  hay $\frac{a}{2}.\frac{1}{2}=\frac{b}{3}.\frac{1}{2}$  tức là $\frac{a}{4}=\frac{b}{6}.$

                  $\frac{b}{2}=\frac{c}{3}$  suy ra $\frac{b}{2}:3=\frac{c}{3}:3$  hay $\frac{b}{2}.\frac{1}{3}=\frac{c}{3}.\frac{1}{3}$  tức là $\frac{b}{6}=\frac{c}{9}.$

   Khi đó $\frac{a}{4}=\frac{b}{6}=\frac{c}{9}$ .

   Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

   $\frac{a}{4}=\frac{b}{6}=\frac{c}{9}=\frac{a+c}{4+9}=\frac{26}{13}=2$.

   Khi đó:

   • $\frac{a}{4}=2$  nên x = 2 . 4 = 8;

   • $\frac{b}{6}=2$  nên y = 2 . 6 = 12;

   • $\frac{c}{9}=2$  nên c = 2 . 9 = 18.

   Vậy a = 8, b = 12, c = 18.

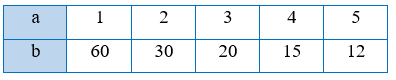
   Bài 2 trang 17 Tập 2: Dựa theo bảng giá trị tương ứng trong mỗi trường hợp sau, hãy cho biết hai đại lượng có tỉ lệ nghịch với nhau hay không.

   a)

   

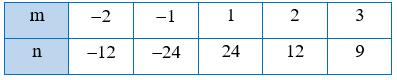
   b)

   

   Lời giải:

   a) Ta có:

   Với a = 1 và b = 60 thì a . b = 1 . 60 = 60;

   Với a = 2 và b = 30 thì a . b = 2 . 30 = 60;

   Với a = 3 và b = 20 thì a . b = 3 . 20 = 60;

   Với a = 4 và b = 15 thì a . b = 4 . 15 = 60;

   Với a = 5 và b = 12 thì a . b = 5 . 12 = 60.

   Khi đó 1 . 60 = 2 . 30 = 3 . 20 = 4 . 15 = 5 . 12 (vì cùng bằng 60).

   Vậy a và b tỉ lệ nghịch với nhau.

   b) Ta có:

   Với m = -2 và n = -12 thì m . n = (-2) . (-12) = 24;

   Với m = -1 và n = -24 thì m . n = (-1) . (-24) = 24;

   Với m = 1 và n = 24 thì m . n = 1 . 24 = 24;

   Với m = 2 và n = 12 thì m . n = 2 . 12 = 24;

   Với m= 3 và n = 9 thì m . n = 3 . 9 = 27.

   Khi đó (-2) . (-12) = (-1) . (-24) = 1 . 24 = 2 . 12 ≠ 3 . 9

   Vậy a và b không tỉ lệ nghịch với  nhau.

   Giải trang 18 Tập 2

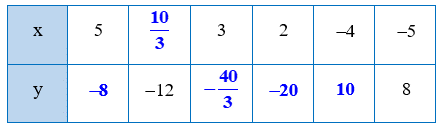
   Bài 3 trang 18 Tập 2: Thay số thích hợp vào dấu ? trong bảng sau sao cho hai đại lượng x và y tỉ lệ nghịch với nhau

   

   Lời giải:

   Để x và y tỉ lệ nghịch với nhau thì xy = (-5) . 8 = -40.

   Suy ra x = $\frac{-40}{y}$  và y = $\frac{-40}{x}.$

   Khi đó:

   • Với x = 5 thì $y=\frac{-40}{5}=-8;$

   • Với y = -12 thì $x=\frac{-40}{-12}=\frac{10}{3};$

   • Với x = 3 thì $y=\frac{-40}{3}=-\frac{40}{3};$

   • Với x = 2 thì $y=\frac{-40}{2}=-20;$

   • Với x = -4 thì $y=\frac{-40}{-4}=10.$

   Vậy ta có bảng sau:

   

   Bài 4 trang 18 Tập 2:

   a) Tìm ba số x, y, z thỏa mãn x : y : z = 1 : 2 : 2 và x + y + z = 25.

   b) Tìm ba số a, b, c thỏa mãn a : b : c = 3 : 4 : 5 và a + b – c = 100.

   Lời giải:

   a) Từ x : y : z = 1 : 2 : 2 ta có $\frac{x}{1}=\frac{y}{2}=\frac{z}{2}$ .

   Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

   $\frac{x}{1}=\frac{y}{2}=\frac{z}{2}=\frac{x+y+z}{1+2+2}=\frac{25}{5}=5$.

   Khi đó:

   • $\frac{x}{1}=5$  nên x = 5 . 1 = 5;

   • $\frac{y}{2}=5$  nên y = 5 . 2 = 10;

   • $\frac{z}{2}=5$  nên y = 5 . 2 = 10.

   Vậy x = 5, y = 10, z = 10.

   b) Từ a : b : c = 3 : 4 : 5 ta có $\frac{a}{3}=\frac{b}{4}=\frac{c}{5}$ .

   Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

   $\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b-c}{3+4-5}=\frac{100}{2}=50.$

    

   Khi đó:

   • $\frac{a}{3}=50$  nên a = 50 . 3 = 150;

   • $\frac{b}{4}=50$  nên b = 50 . 4 = 200;

   • $\frac{c}{5}=50$  nên c = 50 . 5 = 250.

   Vậy a = 150; b = 200; c = 250.

   Bài 5 trang 18 Tập 2: Một nông trường có 4 máy gặt (cùng năng suất) đã gặt xong một cánh đồng hết 6 giờ. Hỏi nếu có 6 máy gặt như thế sẽ gặt xong cánh đồng đó hết bao nhiêu thời gian?

   Lời giải:

   Gọi x (giờ) là thời gian 6 máy gặt sẽ gặt xong cánh đồng đó.

   Do số máy gặt và thời gian gặt xong một cánh đồng là hai đại lượng tỉ lệ nghịch nên áp dụng tính chất của các đại lượng tỉ lệ nghịch ta có:

   6x = 4 . 6 = 24 suy ra $x=\frac{24}{6}=4.$

   Vậy nếu có 6 máy gặt như thế sẽ gặt xong cánh đồng đó hết 4 giờ.

   Bài 6 trang 18 Tập 2: Bạn Cúc muốn cắt một hình chữ nhật có diện tích 100 cm². Gọi d (cm) và r (cm) là hai kích thước của hình chữ nhật. Em hãy viết công thức thể hiện mối quan hệ giữa hai đại lượng d và r.

   Lời giải:

   Diện tích của hình chữ nhật có hai kích thước là d (cm) và r (cm) là dr (cm²).

   Mà diện tích của hình chữ nhật bạn Cúc muốn cắt có diện tích 100 cm² nên dr = 100.

   Vậy công thức thể hiện mối quan hệ giữa hai đại lượng d và r là: dr = 100.

   Bài 7 trang 18 Tập 2: Cho biết a tỉ lệ thuận với b theo hệ số tỉ lệ m và b tỉ lệ thuận với c theo hệ số tỉ lệ n.

   a) Hãy tính a theo b, tính b theo c.

   b) Hãy tính a theo c.

   Lời giải:

   a) Do a tỉ lệ thuận với b theo hệ số tỉ lệ m nên ta có: a = mb.

   Do b tỉ lệ thuận với c theo hệ số tỉ lệ n nên ta có: b = nc.

   Vậy a = mb và b = nc.

   b) Thay b = nc vào a = mb ta có: a = mnc.

   Vậy a = mnc.

   Bài 8 trang 18 Tập 2: Lớp 7A có 4 bạn làm vệ sinh xong lớp học hết 2 giờ. Hỏi nếu có 16 bạn sẽ làm vệ sinh xong lớp học trong bao lâu? (Biết rằng các bạn có năng suất làm việc như nhau).

   Lời giải:

   Gọi x (giờ) là thời gian 16 bạn sẽ làm vệ sinh xong lớp học.

   Do số bạn làm vệ sinh lớp học và thời gian làm xong là hai đại lượng tỉ lệ nghịch nên áp dụng tính chất của các đại lượng tỉ lệ nghịch ta có:

   16x = 4 . 2 = 8 suy ra $x=\frac{8}{16}=\mathrm{0,5}$  giờ = 30 phút.

   Vậy nếu có 16 bạn sẽ làm vệ sinh xong lớp học hết 30 phút.

   Bài 9 trang 18 Tập 2: Hoa muốn chia đều 1 kg đường vào n túi. Gọi p (g) là lượng đường trong mỗi túi. Hãy chứng tỏ n, p là hai đại lượng tỉ lệ nghịch và tính p theo n.

   Lời giải:

   Đổi 1 kg = 1 000 g.

   Bạn Hoa chia đều 1 kilogam đường (1 000 g đường) vào n túi nên khối lượng đường trong mỗi túi là: $\frac{1000}{n}$  (g).

   Mà theo bài p (g) là khối lượng đường trong mỗi túi.

   Do đó p = $\frac{1000}{n}$ .

   Khi đó, n và p là hai đại lượng tỉ lệ nghịch với nhau theo hệ số tỉ lệ là 1 000.

   Vậy công thức tính p theo n là p = $\frac{1000}{n}$

   Bài 10 trang 18 Tập 2: Lớp 7C có 2 bạn dọn xong cỏ vườn trường trong 3 giờ. Hỏi nếu có 6 bạn sẽ dọn xong cỏ vườn trường trong bao lâu? (Biết rằng các bạn có năng suất làm việc như nhau.)

   Lời giải:

   Gọi x (giờ) là thời gian 6 bạn sẽ dọn xong cỏ trong vườn trường.

   Do số bạn dọn cỏ và thời gian các bạn dọn xong cỏ trong vườn là hai đại lượng tỉ lệ nghịch nên áp dụng tính chất của các đại lượng tỉ lệ nghịch ta có:

   6x = 2 . 3 = 6 suy ra $x=\frac{6}{6}=1.$

   Vậy nếu có 6 bạn sẽ dọn xong cỏ vườn trường trong 1 giờ.

   Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

   Bài 3 : Đại lượng tỉ lệ nghịch

   Bài tập cuối chương 6

   Bài 1 : Biểu thức số, biểu thức đại số

   Bài 2 : Đa thức một biến

   Bài 3 : Phép cộng và phép trừ đa thức một biến

4. 30 câu Trắc nghiệm Chương 6: Các đại lượng tỉ lệ (Chân trời sáng tạo) có đáp án 2023 – Toán lớp 7

   Trắc nghiệm Toán 7 Chương 6: Các đại lượng tỉ lệ

   Câu 1:Cho biết x và y là hai đại lượng tỉ lệ thuận. Gọi x₁; x₂ là hai giá trị của x và y₁; y₂là hai giá trị tương ứng của y. Biết rằng x₁ = 8; x₂ = −10và y₁ = 4.Giá trị của y₂ là:

   A. −5;

   B. 24;

   C. 36;

   D. 45.

   Hướng dẫn giải

   Đáp án đúng là: A

   Vì x và y là hai đại lượng tỉ lệ thuận nên $\frac{x_1}{x_2}=\frac{y_1}{y_2}$ (tính chất)

   Thay số ta được $\frac{8}{-10}=\frac{4}{y_2}$

   Suy ra $y_2=\frac{4.(-10)}{8}=-5$

   Vậy y₂ = −5.

   Chọn đáp án A.

   Câu 2: Một ô tô đi trên quãng đường dài 200km với vận tốc là v và thời gian tương ứng t. Công thức tính v theo t là:

   A. v = 200t;

   B. v = $\frac{t}{200}$

   C. v = $\frac{200}{t}$

   D. t = 200v

   Hướng dẫn giải

   Đáp án đúng là: C

   Ta có: vt = s nên vt = 200.

   Suy ra v = $\frac{200}{t}$

   Công thức tính v theo t là v = $\frac{200}{t}$

   Vậy chọn đáp án C.

   Câu 3. Số quyển sách của ba bạn An, Bình, Hải tỉ lệ với các số 2; 4; 5. Tính số sách của mỗi bạn biết rằng cả ba bạn có 44 quyển sách.

   A. 8 quyển, 16 quyển, 20 quyển;

   B. 16 quyển, 20 quyển, 8 quyển;

   C. 20 quyển, 8 quyển, 16 quyển;

   D. 8 quyển, 20 quyển, 16 quyển.

   Hướng dẫn giải

   Đáp án đúng là: A

   Gọi x, y, z (quyển) lần lượt là số sách của ba bạn An, Bình, Hải (x, y, z $\in$ ℕ^*).

   Vì số quyển sách của ba bạn An, Bình, Hải tỉ lệ với các số 2; 4; 5 nên ta có:

   $\frac{x}{2}=\frac{y}{4}=\frac{z}{5}$

   Tổng số sách của cả ba bạn có 44 quyển sách nên x + y + z = 44.

   Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

   $\frac{x}{2}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{2+4+5}=\frac{44}{11}=4$

   Suy ra: x = 4 . 2= 8; y = 4 . 4 =16; z = 4 . 5= 20 (thoả mãn)

   Vậy An có 8 quyển, Bình có 16 quyển, Hải có 20 quyển.

   Chọn đáp án A.

   Câu 4. Hai lớp 7A và 7B trồng cây. Biết rằng số cây trồng được của lớp 7Abằng $\frac{4}{5}$ số cây trồng được của lớp 7B và lớp 7B trồng nhiều hơn lớp 7A là 20 cây. Tính số cây mỗi lớp đã trồng?

   A. Lớp 7A trồng được 80 cây, lớp 7B trồng được 90 cây;

   B. Lớp 7A trồng được 80 cây, lớp 7B trồng được 100 cây;

   C. Lớp 7A trồng được 100 cây, lớp 7B trồng được 80 cây;

   D. Lớp 7A trồng được 90 cây, lớp 7B trồng được 110 cây.

   Hướng dẫn giải

   Đáp án đúng là:B

   Gọi x, y (cây) lần lượt làsố cây lớp 7A và 7B trồng được (x, y $\in$ ℕ*).

   Vì số cây trồng được của lớp 7A bằng $\frac{4}{5}$ số cây trồng được của lớp 7B nên ta có:

   x = $\frac{4}{5}$y suy ra $\frac{x}{y}$ = $\frac{4}{5}$ hay $\frac{x}{4}$ = $\frac{y}{5}$

   Vì lớp 7B trồng nhiều hơn lớp 7A là 20 cây nên ta có: y – x = 20.

   Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

   $\frac{x}{4}=\frac{y}{5}=\frac{y-x}{5-4}=\frac{20}{1}=20$

   Suy ra: x = 20 . 4 = 80; y = 20 . 5 = 100 (thoả mãn)

   Vậy lớp 7A trồng được 80 cây, lớp 7B trồng được 100 cây.

   Chọn đáp án B.

   Câu 5. Ba đội máy san đất làm ba khối lượng công việc như nhau. Đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai trong 6 ngày và đội thứ ba trong 8 ngày. Hỏi mỗi đội có bao nhiêu máy, biết rằng đội thứ nhất nhiều hơn đội thứ hai là 2 máy và các máy có cùng năng suất?

   A. Đội thứ nhất có 3 máy, đội thứ hai có 4 máy, đội thứ ba có 6 máy;

   B. Đội thứ nhất có 4 máy, đội thứ hai có 3 máy, đội thứ ba có 6 máy;

   C. Đội thứ nhất có 6 máy, đội thứ hai có 4 máy, đội thứ ba có 3 máy;

   D. Đội thứ nhất có 6 máy, đội thứ hai có 3 máy, đội thứ ba có 4 máy.

   Hướng dẫn giải

   Đáp án đúng là: C

   Gọi x, y, z (máy) lần lượt là số mấy san của đội thứ nhất, thứ hai và thứ ba(x, y, z $\in$ ℕ^*).

   Vì số máy tỉ lệ nghịch với thời gian hoàn thành công việc nên ta có: 4x = 6y = 8z

   Suy ra: $\frac{x}{6}=\frac{y}{4}=\frac{z}{3}$

   Vì số máy của đội thứ nhất nhiều hơn đội thứ hai 2 máy nên ta có:

   x – y = 2 (máy)

   Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

   $\frac{x}{6}=\frac{y}{4}=\frac{z}{3}=\frac{x-y}{6-4}=\frac{2}{2}=1$

   Suy ra: x = 1 . 6 = 6;y = 1 . 4 = 4; z = 1 . 3 = 3 (thoả mãn điều kiện)

   Vậy số máy san của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là 6 máy, 4 máy, 3 máy.

   Chọn đáp án C.

   Câu 6. Các số x, y thoả mãn 3x = 4y và 2x + y = 20 lần lượt là:

   A. 16 và 12;

   B. 12 và 16;

   C.−12 và 16;

   D. −16 và −12.

   Hướng dẫn giải

   Đáp án đúng là: A

   Ta có 3x = 4y suy ra $\frac{x}{4}$ = $\frac{y}{3}$.

   Theo tính chất dãy tỉ số bằng nhau, ta có:

   $\frac{x}{4}=\frac{y}{3}=\frac{2x-y}{2.4-3}=\frac{20}{5}=4$

   Suy ra x = 4 .4 = 16; y = 3 . 4 = 12.

   Vậy x = 16; y = 12.

   Chọn đáp án A.

   Câu 7. Cho tỉ lệ thức $\frac{x}{3}=\frac{y}{4}=\frac{z}{5}$ và x + y – z = 4. Giá trị của x, y, z lần lượt là:

   A. 10; 8; 6;

   B. 6; 8; 10;

   C. 9; 12; 15;

   D. 15; 12; 9.

   Hướng dẫn giải

   Đáp án đúng là: B

   Theo tính chất dãy tỉ số bằng nhau, ta có:

   $\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y-z}{3+4-5}=\frac{4}{2}=2$

   Suy ra x = 3 . 2 = 6; y = 4 . 2 = 8; z = 5 . 2 = 10.

   Vậy x = 6; y = 8; z = 10.

   Chọn đáp án B.

   Câu 8.Cho tỉ lệ thức x : y : z = 1 : 3 : 4 và 2x + 3y – 2z = −6. Giá trị của x – 2y là:

   A. 12;

   B. 10;

   C. −10;

   D. 14.

   Hướng dẫn giải

   Đáp án đúng là: B

   Theo bài ra x : y : z = 1 : 3 : 4 nên $\frac{x}{1}=\frac{y}{3}=\frac{z}{4}$

   Ta có: $\frac{x}{1}=\frac{2x}{2};\frac{y}{3}=\frac{3z}{9};\frac{z}{4}=\frac{2z}{8}$

   Suy ra: $\frac{x}{1}=\frac{y}{3}=\frac{z}{4}=\frac{2x}{2}=\frac{3y}{9}=\frac{2z}{8}$

   Theo tính chất dãy tỉ số bằng nhau, ta có:

   $\frac{x}{1}=\frac{y}{3}=\frac{z}{4}=\frac{2x}{2}=\frac{3y}{9}=\frac{2z}{8}=\frac{2x+3y-2z}{2+9-8}=\frac{-6}{3}=-2$

   Suy ra x = 1 . (−2) = −2; y = 3 . (−2) = −6.

   Do đó: x – 2y = – 2 – 2.(– 6) = 10.

   Vậy x − 2y = 10.

   Chọn đáp án B.

   Câu 9. Cho tỉ lệ thức 2x = 3y = 4z và x – y + z = −10. Giá trị của x, y, z lần lượt là:

   A. x = −12; y = −8; z = −6;

   B.x = 12; y = 8; z = 4;

   C. x = −6; y = −4; z = −3;

   D. x = 4; y = 6; z = 3.

   Hướng dẫn giải

   Đáp án đúng là: A.

   Theo bài ra 2x = 3y = 4z.

   BCNN(2, 3, 4) = 12.

   Ta có 2x = 3y = 4z nên $\frac{2x}{12}=\frac{3y}{12}=\frac{4z}{12}$

   Suy ra $\frac{x}{6}=\frac{y}{4}=\frac{z}{3}$

   Theo tính chất dãy tỉ số bằng nhau, ta có:

   $\frac{x}{6}=\frac{y}{4}=\frac{z}{3}=\frac{x-y+z}{6-4+3}=\frac{-10}{5}=-2$

   Suy ra x = 6 . (−2) = −12; y = 4 . (−2) = −8; z = 3 . (−2) = −6.

   Vậy x = −12; y = −8; z = −6.

   Chọn đáp án A.

   Câu 10.Cho tỉ lệ thức $\frac{x}{2}=\frac{y}{3};\frac{y}{4}=\frac{z}{5}$ và 2z – 3x = 18. Giá trị của z là:

   A. 30;

   B. 24;

   C. 36;

   D. 45.

   Hướng dẫn giải

   Đáp án đúng là: D

   Theo bài ra $\frac{x}{2}=\frac{y}{3};\frac{y}{4}=\frac{z}{5}$

   BCNN(3, 4) = 12

   Với $\frac{x}{2}=\frac{y}{3}$ suy ra $\frac{x}{8}=\frac{y}{12}$

   Với $\frac{y}{4}=\frac{z}{5}$ suy ra $\frac{y}{12}=\frac{z}{15}$

   Do đó $\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{3x}{24}=\frac{2z}{30}$

   Theo tính chất dãy tỉ số bằng nhau, ta có:

   $\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{3x}{24}=\frac{2z}{30}=\frac{2z-3x}{30-24}=\frac{18}{6}=3$

   Suy ra z = 15 . 3 = 45.

   Vậy z = 45.

   Chọn đáp án D.

   Câu 11. Hai ô tô đi từ A đến B. Vận tốc của xe thứ nhât là 60km/h, của xe thứ hai là 40km/h nên thời gian đi của xe thứ nhất ít hơn xe thứ hai là 30 phút. Tính quãng đường AB?

   A. 45km;

   B. 60km;

   C. 80km;

   D. 75km.

   Hướng dẫn giải

   Đáp án đúng là: B

   Đổi 30 phút = $\frac{1}{2}$giờ.

   Gọi v₁; v₂ (km/giờ) lần lượt là vận tốc của ô tô thứ nhất và ô tô thứ hai (v₁, v₂ > 0).

   Gọi t₁; t₂ (giờ) lần lượt là thời gian của ô tô thứ nhất và ô tô thứ hai (t₁, t₂ > 0).

   Vì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên: v₁.t₁ = v₂.t₂.

   Suy ra 60t₁= 40t₂ hay $\frac{t_1}{40}=\frac{t_2}{60}$

   Mà thời gian đi của xe thứ nhất ít hơn xe thứ hai là 30 phút nên t₂ – t₁ = $\frac{1}{2}$

   Theo bài ra, ta có $\frac{t_1}{40}=\frac{t_2}{60}$ và t₂ – t₁ = $\frac{1}{2}$

   Theo tính chất dãy tỉ số bằng nhau, ta được:

   $\frac{t_1}{40}=\frac{t_2}{60}=\frac{t_2-t_1}{60-40}=\frac{\frac{1}{2}}{20}=\frac{1}{40}$

   Suy ra t₁ = 1 (thoả mãn)

   Quãng đường AB là: v₁ . t₁ = 60 . 1 = 60 (km)

   Vậy quãng đường AB dài 60km.

   Chọn đáp án B.

   Câu 12. Tỉ số giữa số học sinh lớp 7A và 7B là 0,8 và tổng số học sinh của hai lớp 81. Tính số học sinh mỗi lớp.

   A. Lớp 7A có 32 học sinh, lớp 7B có 49 học sinh;

   B. Lớp 7A có 55 học sinh, lớp 7B có 26 học sinh;

   C. Lớp 7A có 36 học sinh, lớp 7B có 45 học sinh;

   D. Lớp 7A có 28 học sinh, lớp 7B có 53 học sinh.

   Hướng dẫn giải

   Đáp án đúng là: C

   Gọi x, y (học sinh) lần lượt là số học sinh hai lớp 7A và 7B (x, y $\in$ ℕ^*)

   Vì tỉ số giữa số học sinh lớp 7A và 7B là 0,8 nên ta có: $\frac{x}{y}$= 0,8 = $\frac{4}{5}$

   Suy ra $\frac{x}{4}$ = $\frac{y}{5}$

   Vì tổng số học sinh của hai lớp là 81 nên ta có: x + y = 81

   Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

   $\frac{x}{4}=\frac{y}{5}=\frac{x+y}{4+5}=\frac{81}{9}=9$

   Suy ra: x = 9 . 4 = 36; y = 9 . 5 = 45 (thoả mãn)

   Vậy số học sinh lớp 7A và 7B lần lượt là 36 học sinh và 45 học sinh.

   Chọn đáp án C.

   Câu 13. Bạn Lan đi từ trường đến nhà với vận tốc 12km/h hết 30 phút. Nếu Lan đi với vận tốc 10km/h thì hết bao nhiêu thời gian?

   A. 25 phút;

   B. 42 phút;

   C. 53 phút;

   D. 36 phút.

   Hướng dẫn giải

   Đáp án đúng là: D

   Gọi x(giờ) là thời gian nếu Lan đi với vân tốc 10 km/h (x>0)

   Đổi: 30 phút = 0,5 giờ.

   Vì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên ta có:

   10 . x = 12 . 0,5 = 6

   Suy ra: x = 6 : 10 = $\frac{3}{5}$ (thoả mãn điều kiện)

   Đổi $\frac{3}{5}$ giờ = 36 phút.

   Vậy nếu Lan đi với vận tốc 10km/h thì hết 36 phút.

   Chọn đáp án D.

   Câu 14. Để làm một công việc trong 8 giờ cần 30 công nhân. Nếu có 40 công nhân thì công việc đó hoàn thành trong mấy giờ? Biết rằng năng suất làm việc của các công nhân là như nhau.

   A. 6 giờ;

   B. 5 giờ;

   C. 7 giờ;

   D. 9 giờ.

   Hướng dẫn giải

   Đáp án đúng là: A

   Gọi x (giờ) là thời gian hoàn thành công việc nếu có 40 công nhân (x>0)

   Vì số công nhân và thời gian làm việc tỉ lệ nghịch nên ta có:

   40 . x = 8 . 30 = 240

   Suy ra: x = 240 : 40 = 6 (thoả mãn điều kiện)

   Vậy nếu có 40 công nhân thì đội hoàn thành công việc trong 6 giờ.

   Chọn đáp án A.

   Câu 15. Cho x và y là hai đại lượng tỉ lệ thuận. Gọi x₁; x₂ là hai giá trị của x và y₁; y_2­ là hai giá trị tương ứng của y. Biết rằng x₁ = 8; x₂ = −10và y₁− y₂ = 9. Tính y₁; y_2­ và biểu diễn y theo x.

   

   Hướng dẫn giải

   Đáp án đúng là: D

   Vì x và y là hai đại lượng tỉ lệ thuận nên ta có: $\frac{x}{y}=\frac{x_1}{y_1}=\frac{x_2}{y_2}$

   Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

   $\frac{x}{y}=\frac{x_1}{y_1}=\frac{x_2}{y_2}=\frac{x_1-x_2}{y_1-y_2}=\frac{18}{9}=2$

   Suy ra: $y_1=\frac{1}{2}{x}_1$ = $\frac{1}{2}.8$ = 4; $y_2=\frac{1}{2}{x}_2$ = $\frac{1}{2}.(-10)$ = -5

   Khi đó: $y=\frac{1}{2}x$

   Vậy $y_1=4$; $y_2=-5$; y = $\frac{1}{2}x$

   Chọn đáp án D.

   Câu 16. Các tỉ số nào sau đây lập thành một tỉ lệ thức?

   

   Hướng dẫn giải

   Đáp án đúng là: D

   Ta có:

   

   Suy ra $(-1):\frac{2}{5}=$$\frac{-5}{3}:\frac{4}{6}$ $=\frac{-5}{2}$

   Do đó, (-1) : $\frac{2}{5}$và $\frac{–5}{3}:\frac{4}{6}$ lập thành một tỉ lệ thức.

   Vậy chọn đáp án D.

   Câu 17. Chọn câu sai. Nếu $\frac{a}{b}=\frac{c}{d}=\frac{m}{n}$ thì:

   

   Hướng dẫn giải

   Đáp án đúng là: B

   Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

   $\frac{a}{b}=\frac{c}{d}=\frac{m}{n}=\frac{a+c-m}{b+d-n}\ne \frac{a+c-m}{b+n-d}$

   Vậy chọn đáp án B.

   Câu 18.Chọn câu sai. Từ đẳng thức −2x = 3y, ta có tỉ lệ thức:

   

   Hướng dẫn giải

   Đáp án đúng là: C

   Theo bài ra −2x = 3y. Suy ra $\frac{x}{y}=\frac{3}{-2}$ (tính chất tỉ lệ thức)

   Nếu $\frac{x}{-2}=\frac{y}{3}$ thì $\frac{x}{y}=\frac{-2}{3}\ne \frac{3}{-2}$

   Do đó $\frac{x}{-2}=\frac{y}{3}$ là sai

   Vậy chọn đáp án C.

   Câu 19. Cho hai số dương x, y thoả mãn $\frac{x}{3}=\frac{y}{5}$ và xy = 60. Khi đó x, y bằng

   A. x = 6; y = 10;

   B. x = 10; y = 6;

   C. x = −6; y = −10;

   D. x = −10; y = −6.

   Hướng dẫn giải

   Đáp án đúng là: A

   Đặt $\frac{x}{3}=\frac{y}{5}$ = k. Suy ra x = 3k; y = 5k

   Theo bài ra xy = 60 nên ta có:

   3k . 5k = 60

   15k² = 60

   k² = 4

   Suy ra k = 2 hoặc k = −2.

   Với k = 2 thì x = 3. 2 = 6; y = 5 . 2 = 10

   Với k = −2 thì x = 3.(−2)= −6; y = 5 . (−2) = −10

   Mà x,y là các số dương nên x = 6; y = 10.

   Vậy chọn đáp án A.

   Câu 19. Một hình chữ nhật có chu vi 56 m, tỉ số của chiều dài và chiều rộng là 5: 2. Diện tích của hình chữ nhật đó là:

   A. 80;

   B. 640;

   C. 320;

   D. 160.

   Hướng dẫn giải

   Đáp án đúng là: D

   Gọi x, y (m) lần lượt là chiều dài và chiều rộng của hình chữ nhật (0 < x, y < 56).

   Nửa chu vi hình chữ nhật là: x + y = 56 : 2 = 28 (m)

   Tỉ số của chiều dài và chiều rộng là 5 : 2 nên $\frac{x}{y}=\frac{5}{2}$ hay $\frac{x}{5}=\frac{y}{2}$

   Áp dụng tính chất dãy tỉ số bằng nhau ta có:

   $\frac{x}{5}=\frac{y}{2}=\frac{x+y}{5+2}=\frac{28}{7}=4$

   Suy ra x = 5 . 4 = 20; y = 2 . 4 = 8 (thoả mãn điều kiện)

   Khi đó, hình chữ nhật có chiều dài là 20 m và chiều rộng là 8 m.

   Vậy diện tích hình chữ nhật là: 20 . 8 = 160 (m²).

   Vậy chọn đáp án D.

   Câu 20. Cho đại lượng y tỉ lệ thuận với đại lượng x theo hệ số k (k ≠ 0). Gọi x₁; x₂ là các giá trị của đại lượng x và y₁; y₂ là các giá trị của đại lượng y tương ứng, biết x₁= 2,5 thìy₁ = −0,5. Hãy tính x₂ khi y₂ = 5.

   A. x₂= −0,25;

   B. x₂= 5;

   C. x₂= −25;

   D. x₂= 10.

   Hướng dẫn giải

   Đáp án đúng: C

   Vì y tỉ lệ thuận với đại lượng x theo hệ số k nên ta có $\frac{x_1}{x_2}=\frac{y_1}{y_2}$

   Thay số $\frac{2,5}{x_2}=\frac{-0,5}{5}$

   Suy ra $x_2=\frac{2,5.5}{-0,5}=-25$

   Chọn đáp án C.

   Câu 21. Một công nhân làm được 20 sản phẩm trong 40 phút. Trong 60 phút người đó làm được bao nhiêu sản phẩm cùng loại?

   A. 10 sản phẩm;

   B. 30 sản phẩm;

   C. 15 sản phẩm;

   D. 35 sản phẩm.

   Hướng dẫn giải

   Đáp án đúng là: B

   Gọi x (sản phẩm) là số sản phẩm người đó làm trong 60 phút (x $\in$ ℕ^*).

   Vì số sản phẩm tỉ lệ thuận với thời gian làm sản phẩm nên ta có:

   $\frac{x}{20}$ = $\frac{60}{40}$

   Suy ra x = $\frac{60}{40}$. 20 = 30 (thỏa mãn điều kiện).

   Vậy trong 60 phút người đó làm được 30 sản phẩm.

   Chọn đáp án B.

   Câu 22. Giả sử x và y là hai đại lượng tỉ lệ thuận x₁, x₂ là hai giá trị khác nhau của x có tổng bằng 4 và y₁, y₂ là hai giá trị của y có tổng bằng 5. Biểu diễn y theo x là:

   

   Hướng dẫn giải

   Đáp án đúng là: A

   Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

   $\frac{x}{y}=\frac{x_1+x_2}{y_1+y_2}=\frac{4}{5}$

   Suy ra y = $\frac{5}{4}$x

   Vậy biểu diễn y theo x là y = $\frac{5}{4}$x

   Chọn đáp án A.

   Câu 23. Một hình chữ nhật có hai cạnh tỉ lệ lần lượt với 9 và 6, chu vi là 300 cm. Chiều dài và chiều rộng của hình chữ nhật lần lượt là:

   A. 40 cm và 60 cm;

   B. 90 cm và 60 cm;

   C. 40 cm và 90 cm;

   D. 60 cm và 40 cm.

   Hướng dẫn giải

   Đáp án đúng là: B

   Gọi x, y (m) lần lượt là chiều dài và chiều rộng của hình chữ nhật (0 < x, y < 150)

   Nửa chu vi hình chữ nhật là:

   x + y = 300 : 2 = 150 (m).

   Hai cạnh của hình chữ nhật tỉ lệ với 9 và 6. Tức là chiều dài và chiều rộng của hình chữ nhật tỉ lệ với 9 và 6 nên ta có: $\frac{x}{9}=\frac{y}{6}$

   Áp dụng tính chất dãy tỉ số bằng nhau ta có:

   $\frac{x}{9}=\frac{y}{6}=\frac{x+y}{9+6}=\frac{150}{15}=10$

   Suy ra x = 9 . 10 = 90; y = 6 . 10 = 60 (thỏa mãn điều kiện)

   Vậy hình chữ nhật có chiều dài là 90 m, chiều rộng là 60 m.

   Chọn đáp án B.

   Câu 24. Hai thanh sắt có thể tích là 26 cm³ và 13 cm³. Thanh thứ nhất nặng hơn thanh thứ hai 56 g. Hỏi thanh thứ hai nặng có khối lượng bằng bao nhiêu?

   A. 56 g;

   B. 112 g;

   C. 168 g;

   D. 28 g.

   Hướng dẫn giải

   Đáp án đúng là: A

   Gọi V₁, V₂ (cm³) lần lượt là thể tích của thanh thứ nhất và thanh thứ hai (V₁, V₂ > 0)

   Gọi m₁, m­₂ (g) lần lượt là khối lượng của thanh thứ nhất và thanh thứ hai (m₁, m₂ > 0).

   Vì thể tích và khối lượng tỉ lệ thuận với nhau nên:

   $\frac{m_1}{m_2}=\frac{26}{13}=2$

   Suy ra: m₁ = 2m₂.

   Theo đề bài, thanh thứ nhất nặng hơn thanh thứ hai 56 g nên ta có:

   m₁ – m₂ = 56.

   Suy ra: 2m₂ – m₂ = 56.

   Do đó: m₂ = 56

   Vậy thanh thứ hai nặng 56 g.

   Vậy chọn đáp án A.

   Câu 25. Một tổ sản xuất tuyển x (công nhân) để hoàn thành 180 sản phẩm, biết mỗi công nhân phải làm y (sản phẩm). Hỏi x có quan hệ như thế nào với y?

   A. x tỉ lệ nghịch với y theo hệ số $\frac{1}{180}$;

   B. x tỉ lệ thuận với y theo hệ số $\frac{1}{180}$;

   C. x tỉ lệ nghịch với y theo hệ số 180;

   D. x tỉ lệ thuận với y theo hệ số 180.

   Hướng dẫn giải

   Đáp án đúng là: C

   Vì số công nhân càng nhiều thì thời gian làm càng ít nên số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.

   Suy ra xy = 180.

   Vậy chọn đáp án C.

   Câu 26. Có 15 công nhân với năng suất như nhau đóng xong một chiếc tàu trong 40 ngày. Hỏi cần bao nhiêu công nhân để đóng xong một con tàu trong 30 ngày?

   A. 20 công nhân;

   B. 10 công nhân;

   C. 25 công nhân;

   D. 5 công nhân.

   Hướng dẫn giải

   Đáp án đúng là: A

   Gọi x (công nhân) là số công nhân cần để đóng xong tàu trong 30 ngày (x $\in$ ℕ*)

   Vì số công nhân và thời gian làm việc tỉ lệ nghịch với nhau nên ta có: $\frac{x}{15}=\frac{40}{30}$

   Suy ra x = $\frac{40}{30}.15$ = 20 (thỏa mãn điều kiện)

   Vậy cần 20 công nhân để đóng xong một con tàu trong 30 ngày.

   Chọn đáp án A.

   Câu 27. Bạn Giang đi xe đạp với vân tốc 3km/h đến trường mất 10 phút. Hỏi nếu bạn Giang đi xe điện đến trường với vận tốc 5 km/h mất bao nhiêu phút?

   A. 6 phút;

   B. 15 phút;

   C. 5 phút;

   D. 12 phút.

   Hướng dẫn giải

   Đáp án đúng là: A

   Gọi x (giờ) là thời gian bạn Giang đi bằng xe điện (x > 0)

   Đổi 10 phút = giờ.

   Vì vận tốc và thời gian là 2 đại lượng tỉ lệ nghịch nên ta có:

   $5.x=3.\frac{1}{6}=\frac{1}{2}$

   Suy ra $x=\frac{1}{2}:5=\frac{1}{10}$ (thỏa mãn)

   Đổi $\frac{1}{10}$ giờ = 6 phút.

   Vậy chọn đáp án A.

   Câu 28. Cứ 100 kg thóc thì thu được 70 kg gạo. Hỏi để thu được 140 kg gạo thì cần bao nhiêu tạ thóc?

   A. 200 tạ;

   B. 2 tạ;

   C. 98 tạ;

   D. 50 tạ.

   Hướng dẫn giải

   Đáp án đúng là: B

   Gọi x (kg) là số kg thóc cần để thu được 140 kg gạo (x > 0)

   Vì số gạo và số thóc tỉ lệ thuận với nhau nên ta có:

   $\frac{x}{140}=\frac{100}{70}$

   Suy ra x = $\frac{100}{70}$.140 = 200 (thỏa mãn điều kiện)

   Nên x = 200 (kg)

   Đổi 200 kg = 2 tạ.

   Vậy để thu được 140 kg gạo thì cần 2 tạ thóc.

   Chọn đáp án B.

   Câu 29. Dùng 15 máy thì tiêu thụ hết 90 lít xăng. Hỏi dùng 25 máy (cùng loại) thì tiêu thụ hết bao nhiêu lít xăng?

   A. 54 lít;

   B. 270 lít;

   C. 150 lít;

   D. 95 lít.

   Hướng dẫn giải

   Đáp án đúng là: C

   Gọi x (lít) là số lít xăng cần dùng để tiêu thụ cho 25 máy (x > 0).

   Số máy và số lít xăng tỉ lệ thuận với nhau nên ta có:

   $\frac{x}{25}$ = $\frac{90}{15}$ = 6.

   Suy ra x = 6 . 25 = 150 (thoả mãn điều kiện).

   Vậy dùng 25 máy (cùng loại) thì tiêu thụ hết 150 lít xăng.

   Chọn đáp án C.

   Câu 30. Giả sử x và y là hai đại lượng tỉ lệ thuận x₁, x₂ là hai giá trị khác nhau của x có giá trị lần lượt là 3 và −5 và y₁; y₂ là hai gía trị của y sao cho 2y₁ + y₂ = 2. Biểu diễn x theo y.

   A. x = $\frac{1}{2}$y;

   B. x = 2y;

   C. x = −2y;

   D. x = $\frac{–1}{2}$y.

   Hướng dẫn giải

   Đáp án đúng là: A

   Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ k.

   Khi đó y = kx. Suy ra k = $\frac{y}{x}$

   Theo tính chất của đại lượng tỉ lệ thuận $\frac{y_1}{x_1}=\frac{y_2}{x_2}$

   Với x₁ = 3; x₂ = −5 ta có nên $\frac{y_1}{3}=\frac{y_2}{-5}$.

   Theo tính chất dãy tỉ số bằng nhau, ta có:

   $\frac{y_1}{3}=\frac{y_2}{-5}=\frac{2y_1+y_2}{2.3-5}=\frac{2}{1}=2$

   Suy ra $\frac{y}{x}=\frac{y_1}{x_1}=\frac{y_2}{x_2}=2$

   Vậy biểu diễn x theo y là $\frac{1}{2}$y.

   Chọn đáp án A.

   Xem thêm các bài trắc nghiệm Toán 7 Chân trời sáng tạo hay, chi tiết khác:

   Trắc nghiệm Toán 7 Bài 3: Đại lượng tỉ lệ nghịch

   Trắc nghiệm Ôn tập chương 6

   Trắc nghiệm Toán 7 Bài 1: Biểu thức số, biểu thức đại số

   Trắc nghiệm Toán 7 Bài 2: Đa thức một biến

   Trắc nghiệm Toán 7 Bài 3: Phép cộng và phép trừ đa thức một biến

5. Giải SGK Toán 7 (Kết nối tri thức) Bài tập cuối chương 6

   Giải bài tập Toán lớp 7 Bài tập cuối chương 6

    

   Giải Toán 7 trang 20 Tập 2

   Bài 6.33 Trang 20 Toán lớp 7: Lập tất cả các tỉ lệ thức có thể được từ bốn số sau: 0,2; 0,3; 0,8; 1,2.

   Phương pháp giải:

   Bước 1: Tìm đẳng thức có được từ 4 số trên.

   Bước 2: Với a.d= b.c (a,b,c,d $\ne$ 0), ta có các tỉ lệ thức:

   $\frac{a}{b}=\frac{c}{d};\frac{a}{c}=\frac{b}{d};\frac{d}{b}=\frac{c}{a};\frac{d}{c}=\frac{b}{a}$

   Lời giải:

   Ta có: 0,2 . 1,2 = 0,3 . 0,8

   Các tỉ lệ thức có thể được là:

   $\frac{0,2}{0,3}=\frac{0,8}{1,2};\frac{0,2}{0,8}=\frac{0,3}{1,2};\frac{1,2}{0,3}=\frac{0,8}{0,2};\frac{1,2}{0,8}=\frac{0,3}{0,2}$

   Bài 6.34 Trang 20 Toán lớp 7: Tìm thành phần chưa biết x trong tỉ lệ thức: $\frac{x}{2,5}=\frac{10}{15}$

   Phương pháp giải:

   Áp dụng tính chất của tỉ lệ thức: Nếu $\frac{a}{b}=\frac{c}{d}$ thì a.d = b.c

   Lời giải:

   Vì $\frac{x}{2,5}=\frac{10}{15}$ nên x. 15 = 2,5 . 10 $\Rightarrow 15.x=25\Rightarrow x=\frac{25}{15}=\frac{5}{3}$

   Vậy $x=\frac{5}{3}$

   Bài 6.35 Trang 20 Toán lớp 7: Từ tỉ lệ thức $\frac{a}{b}=\frac{c}{d}$ ( với a,b,c,d khác 0) có thể suy ra những tỉ lệ thức nào?

   Phương pháp giải:

   Áp dụng tính chất của tỉ lệ thức: Nếu $\frac{a}{b}=\frac{c}{d}$ thì a.d = b.c

   Với a.d= b.c (a,b,c,d $\ne$ 0), ta có các tỉ lệ thức:

   $\frac{a}{b}=\frac{c}{d};\frac{a}{c}=\frac{b}{d};\frac{d}{b}=\frac{c}{a};\frac{d}{c}=\frac{b}{a}$

   Lời giải:

   Ta có: $\frac{a}{b}=\frac{c}{d}$ nên a.d = b.c

   Ta suy ra được các tỉ lệ thức: $\frac{a}{c}=\frac{b}{d};\frac{d}{b}=\frac{c}{a};\frac{d}{c}=\frac{b}{a}$

   Bài 6.36 Trang 20 Toán lớp 7: Inch ( đọc là in-sơ và viết tắt là in) là tên của một đơn vị chiều dài trong Hệ đo lường Mĩ. Biết rằng 1 in = 2,54 cm.

   a) Hỏi một người cao 170 cm sẽ có chiều cao là bao nhiêu inch (làm tròn kết quả đến hàng đơn vị)?

   b) Chiều cao của một người tính theo xentimet có tỉ lệ thuận với chiều cao của người đó tính theo inch không? Nếu có thì hệ số tỉ lệ là bao nhiêu?

   Phương pháp giải:

   Chiều dài (theo cm) = 2,54. Chiều dài (theo inch)

   Lời giải:

   a) Chiều cao của người đó là:

   170 : 2,54 $\approx$66,9 $\approx$67 ( inch)

   b) Chiều cao của một người tính theo xentimet có tỉ lệ thuận với chiều cao của người đó tính theo inch vì chúng liên hệ với nhau theo công thức: Chiều dài (theo cm) = 2,54. Chiều dài (theo inch)

   Hệ số tỉ lệ là 2,54.

   Bài 6.37 Trang 20 Toán lớp 7: Số đo ba góc $\hat{A},\hat{B},\hat{C}$ của tam giác ABC tỉ lệ với 5;6;7. Tính số đo ba góc của tam giác đó.

   Phương pháp giải:

   Tổng 3 góc của 1 tam giác bằng 180 độ.

   Áp dụng tính chất của dãy tỉ số bằng nhau:$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{a+c+e}{b+d+f}$

   Lời giải:

   Trong tam giác ABC có: $\hat{A}+\hat{B}+\hat{C}={180}^{\circ }$

   Mà số đo ba góc $\hat{A},\hat{B},\hat{C}$ của tam giác ABC tỉ lệ với 5;6;7 nên $\frac{\hat{A}}{5}=\frac{\hat{B}}{6}=\frac{\hat{C}}{7}$

   Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

   $\begin{array}{l}\frac{\hat{A}}{5}=\frac{\hat{B}}{6}=\frac{\hat{C}}{7}=\frac{\hat{A}+\hat{B}+\hat{C}}{5+6+7}=\frac{{180}^{\circ }}{18}={10}^{\circ }\\ \Rightarrow \hat{A}={10}^{\circ }.5={50}^{\circ }\\ \hat{B}={10}^{\circ }.6={60}^{\circ }\\ \hat{C}={10}^{\circ }.7={70}^{\circ }\end{array}$

   Vậy số đo 3 góc $\hat{A},\hat{B},\hat{C}$ lần lượt là ${50}^{\circ };{60}^{\circ };{70}^{\circ }$

   Bài 6.38 Trang 20 Toán lớp 7: Ba đội công nhân làm đường được giao ba khối lượng công việc như nhau. Đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai trong 5 ngày và đội thứ ba trong 6 ngày. Tính số công nhân của mỗi đội biết đội thứ nhất nhiều hơn đội thứ hai là 3 người và năng suất của các công nhân là như nhau trong suốt quá trình làm việc.

   Phương pháp giải:

   Gọi số công nhân mỗi đội lần lượt là x,y,z (người) (x,y,z $\in$N*).

   Số công nhân và thời gian hoàn thành là 2 đại lượng tỉ lệ nghịch

   Sử dụng tính chất của dãy tỉ số bằng nhau: $\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{a-c}{b-d}$

   Lời giải:

   Gọi số công nhân mỗi đội lần lượt là x,y,z (người) (x,y,z $\in$N*).

   Vì số công nhân của đội thứ nhất nhiều hơn số công nhân của đội thứ hai là 3 người nên x – y = 3

   Vì khối lượng công việc là như nhau và năng suất của các máy như nhau nên số công nhân và thời gian hoàn thành là 2 đại lượng tỉ lệ nghịch.

   Áp dụng tính chất của hai đại lượng tỉ lệ nghịch, ta có:

   4x=5y=6z

   $\begin{array}{l}\Rightarrow \frac{x}{\frac{1}{4}}=\frac{y}{\frac{1}{5}}=\frac{z}{\frac{1}{6}}=\frac{x-y}{\frac{1}{4}-\frac{1}{5}}=\frac{3}{\frac{1}{20}}=3:\frac{1}{20}=3.20=60\\ \Rightarrow x=60.\frac{1}{4}=15\\ y=60.\frac{1}{5}=12\\ z=60.\frac{1}{6}=10\end{array}$

   Vậy 3 đội có lần lượt là 15; 12 và 10 công nhân.

   Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

   Luyện tập chung trang 19

   Bài 24: Biểu thức đại số

   Bài 25: Đa thức một biến

   Bài 26: Phép cộng và phép trừ đa thức một biến