Cho tam giác ABC, biết AB = 21cm, AC = 28cm, BC = 35cm. Chứng minh tam giác ABC vuông

Câu hỏi:

Cho tam giác ABC, biết AB = 21cm, AC = 28cm, BC = 35cm. Chứng minh tam giác ABC vuông

Trả lời:

Ta có:  $A{B}^2={21}^2=441A{C}^2={28}^2=784B{C}^2={35}^2=1225$ Vì $A{B}^2+A{C}^2$ = 441 + 784 = 1225 = $B{C}^2$ nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Giải SGK Toán 8 Ôn tập chương 1 Hình học

   Giải bài tập Toán lớp 8 Ôn tập chương 1 Hình học

   Trả lời câu hỏi giữa bài

   Câu hỏi 1 trang 110 Toán 8 Tập 1: Phát biểu định nghĩa tứ giác.

   Trả lời:

   Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

   Câu hỏi 2 trang 110 Toán 8 Tập 1:Phát biểu định nghĩa hình thang, hình thang cân.

   Trả lời:

   – Hình thang là tứ giác có hai cạnh đối song song.

   – Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

   Câu hỏi 3 trang 110 Toán 8 Tập 1:Phát biểu các tính chất của hình thang cân.

   Trả lời:

   Tính chất:

   – Định lí 1: Trong hình thang cân, hai cạnh bên bằng nhau.

   – Định lí 2: Trong hình thang cân, hai đường chéo bằng nhau.

   Câu hỏi 4 trang 110 Toán 8 Tập 1:Phát biểu các tính chất của đường trung bình của tam giác, đường trung bình của hình thang.

   Trả lời:

   – Đường trung bình của tam giác:

       + Định lí 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

       + Định lí 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

   – Đường trung bình của hình thang:

       + Định lí 3: Đường thẳng đi qua trung điểm của một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.

       + Định lí 4: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

   Câu hỏi 5 trang 110 Toán 8 Tập 1: Phát biểu định nghĩa hình bình hành, hình chữ nhật, hình thoi, hình vuông.

   Trả lời:

   – Hình bình hành là tứ giác có các cạnh đối song song.

   – Hình chữ nhật là tứ giác có bốn góc vuông.

   – Hình thoi là tứ giác có bốn cạnh bằng nhau.

   – Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.

   Câu hỏi 6 trang 110 Toán 8 Tập 1:Phát biểu các tính chất của hình bình hành, hình chữ nhật, hình thoi, hình vuông.

   Trả lời:

   Tính chất:

   – Hình bình hành:

   Trong hình bình hành:

   a) Các cạnh đối bằng nhau.

   b) Các góc đối bằng nhau.

   c) Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

   – Hình chữ nhật:

   Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

   – Hình thoi:

   Trong hình thoi:

   a) Hai đường chéo vuông góc với nhau.

   b) Hai đường chéo là các đường phân giác của các góc của hình thoi.

   – Hình vuông:

   Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.

   Câu hỏi 7 trang 110 Toán 8 Tập 1:Nêu các dấu hiệu nhận biết hình bình hành, hình chữ nhật, hình thoi, hình vuông.

   Trả lời:

   Dấu hiệu nhận biết:

   – Hình bình hành:

   1) Tứ giác có các cạnh đối song song là hình bình hành.

   2) Tứ giác có các cạnh đối bằng nhau là hình bình hành.

   3) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

   4) Tứ giác có các góc đối bằng nhau là hình bình hành.

   5) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

   – Hình chữ nhật:

   1) Tứ giác có ba góc vuông là hình chữ nhật.

   2) Hình thang cân có một góc vuông là hình chữ nhật.

   3) Hình bình hành có một góc vuông là hình chữ nhật.

   4) Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

   – Hình thoi:

   1) Tứ giác có bốn cạnh bằng nhau là hình thoi.

   2) Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

   3) Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

   4) Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

   – Hình vuông:

   1) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

   2) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

   3) Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.

   4) Hình thoi có một góc vuông là hình vuông.

   5) Hình thoi có hai đường chéo bằng nhau là hình vuông.

   Câu hỏi 8 trang 110 Toán 8 Tập 1:Thế nào là hai điểm đối xứng với nhau qua một đường thẳng? Trục đối xứng của hình thang cân là đường thẳng nào?

   Trả lời:

   – Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.

   – Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm hai đáy của hình thang cân.

   Câu hỏi 9 trang 110 Toán 8 Tập 1:Thế nào là hai điểm đối xứng với nhau qua một điểm? Tâm đối xứng của hình bình hành là điểm nào?

   Trả lời:

   – Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.

   – Tâm đối xứng của hình bình hành là giao điểm hai đường chéo của hình bình hành đó.

   Bài tập (trang 111)

   Bài 87 trang 111 Toán 8 Tập 1:Sơ đồ ở hình 109 biểu thị quan hệ giữa các tập hợp hình thang, hình bình hành, hình chữ nhật, hình thoi, hình vuông. Dựa vào sơ đồ đó, hãy điền vào chỗ trống:

   a) Tập hợp các hình chữ nhật là tập hợp con của tập hợp các hình …

   b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình …

   c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình …

   

   Hình 109

   Lời giải:

   a) Tập hợp các hình chữ nhật là tập hợp con của tập hợp các hình bình hành, hình thang.

   b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình bình hành, hình thang.

   c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình vuông.

   Bài 88 trang 111 Toán 8 Tập 1:Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD có điều kiện gì thì EFGH là:

   a) Hình chữ nhật?

   b) Hình thoi?

   c) Hình vuông?

   Lời giải:

   

   Xét $\Delta ABC$, có:

   E là trung điểm của AB

   F là trung điểm của BC

   ⇒ EF là đường trung bình của ΔABC

   ⇒ EF // AC và $FE=\frac{AC}{2}$ (1).

   Xét $\Delta ADC$, ta có:

   H là trung điểm của AD

   G là trung điểm của CD

   ⇒ HG là đường trung bình của ΔADC

   ⇒ HG // AC và $HG=\frac{AC}{2}.$(2)

   Từ (1) và (2) suy ra EF // HG, EF = HG

   ⇒ EFGH là hình bình hành.

   a) Hình bình hành EFGH là hình chữ nhật ⇔ EH ⊥ EF

   Mà EF // AC

   $\Rightarrow AC\perp EH$(3)

   Xét $\Delta ABD$, có:

   E là trung điểm của AB

   H là trung điểm của AD

   ⇒ EH là đường trung bình của ΔABD

   ⇒ EH // BD và $EH=\frac{BD}{2}$ (4)

   Từ (3) và (4) suy ra AC ⊥ BD

   b) Hình bình hành EFGH là hình thoi

   ⇔ EF = EH

   ⇔ AC = BD (Vì $\text{EF}=\frac{AC}{2},EH=\frac{BD}{2}$)

   c) EFGH là hình vuông

   ⇔ EFGH là hình thoi và EFGH là hình chữ nhật

   ⇔ AC = BD và AC ⊥ DB.

   Bài 89 trang 111 Toán 8 Tập 1:Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm dối xứng với M qua D.

   a) Chứng minh rằng điểm E đối xứng với điểm M qua AB.

   b) Các tứ giác AEMC, AEBM là hình gì? Vì sao?

   c) Cho BC = 4cm, tính chu vì tứ giác AEBM.

   d) Tam giác vuông ABC có điều kiện gì thì AEBM là hình vuông?

   Lời giải:

   

   a) Xét $\Delta ABC$, ta có:

   MB = MC, DB = DA

   ⇒ MD là đường trung bình của ΔABC

   ⇒ MD // AC, $MD=\frac{AC}{2}$

   Mà AC ⊥ AB

   ⇒ MD ⊥ AB.

   Mà D là trung điểm ME

   ⇒ AB là đường trung trực của ME

   ⇒ E đối xứng với M qua AB.

   b) + MD là đường trung bình của ΔABC

   ⇒ AC = 2MD (cmt).

   E đối xứng với M qua D

   ⇒ D là trung điểm EM

   ⇒ EM = 2.MD

   ⇒ AC = EM.

   Lại có AC // EM

   ⇒ Tứ giác AEMC là hình bình hành.

   + Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.

   Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.

   c) Ta có: BC = 4cm ⇒ BM = 2cm

   (vì M là trung điểm của BC)

   Chu vi hình thoi AEBM bằng

   4.BM = 4.2 = 8cm

   d)- Cách 1:

   Hình thoi AEBM là hình vuông ⇔ AB = EM

   Mà EM = AC

   ⇔ AB = AC

   Vậy nếu ABC vuông có thêm điều kiện AB = AC (tức tam giác ABC vuông cân tại A) thì AEBM là hình vuông.

   – Cách 2:

   Hình thoi AEBM là hình vuông

   $\iff \widehat{AMB}={90}^0$

   ⇔ AM ⊥ BM

   ⇔ ΔABC có trung tuyến AM là đường cao

   ⇔ ΔABC cân tại A.

   Vậy nếu ΔABC vuông có thêm điều kiện cân tại A thì AEBM là hình vuông.

   Bài 90 trang 111 Toán 8 Tập 1:Đố. Tìm trục đối xứng và tâm đối xứng của:

   a) Hình 110 (sơ đồ một sân quần vợt)

   b) Hình 111 (Tháp Rùa là bóng của nó trên mặt nước)

   

   

   Lời giải

   

   

   a) Hình 110:

   Sân quần vợt có dạng hình chữ nhật nên nó cũng là hình thang cân nên trục đối xứng chính là đường thẳng nối trung điểm của hai cạnh đối diện.

   – Hai trục đối xứng là AB và CD.

   – Một tâm đối xứng là O.

   b) Hình 111

   – Hai trục đối xứng là MN và PQ

   – Một tâm đối xứng là I.

2. Giải SGK Toán 8 Ôn tập chương 1 Đại số

   Giải bài tập Toán lớp 8 Ôn tập chương 1

   Trả lời câu hỏi giữa bài

   Câu hỏi 1 trang 32 Toán 8 Tập 1: Phát biểu các qui tắc nhân đơn thức với đa thức, nhân đa thức với đa thức.

   Lời giải

   – Nhân đơn thức với đa thức: Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.

   – Nhân đa thức với đa thức: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.

   Câu hỏi 2 trang 32 Toán 8 Tập 1: Viết bảy hằng đẳng thức đáng nhớ.

   Lời giải:

   Bảy hằng đẳng thức đáng nhớ:

   1) (A + B)² = A² + 2AB + B²

   2) (A – B)² = A² – 2AB + B²

   3) A² – B² = (A – B)(A + B)

   4) (A + B)³ = A³ + 3A²B + 3AB² + B³

   5) (A – B)³ = A³ – 3A²B + 3AB² – B³

   6) A³ + B³ = (A + B)(A² – AB + B²)

   7) A³ – B³ = (A – B)(A² + AB + B²)

   Câu hỏi 3 trang 32 Toán 8 Tập 1: Khi nào thì đơn thức A chia hết cho đơn thức B?

   Lời giải:

   Đơn thức A chia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.

   Câu hỏi 4 trang 32 Toán 8 Tập 1: Khi nào thì đa thức A chia hết cho đơn thức B?

   Lời giải:

   Khi từng hạng tử của đa thức A đều chia hết cho đơn thức B thì đa thức A chia hết cho đơn thức B.

   Câu hỏi 5 trang 32 Toán 8 Tập 1: Khi nào thì đa thức A chia hết cho đa thức B?

   Lời giải:

   Khi đa thức A chia hết cho đa thức B được dư bằng 0 thì ta nói đa thức A chia hết cho đa thức B.

   Bài tập (trang 33)

   Bài 75 trang 33 Toán 8 Tập 1: Làm tính nhân:

   a) 5x².(3x² – 7x + 2);

   b) $\frac{2}{3}xy.\left(2x^{2}y-3xy+y^2\right).$

   Lời giải:

   a) 5x².(3x² – 7x + 2)

   = 5x².3x² – 5x².7x + 5x².2

   = (5.3).(x².x²) – 5.7.(x².x) + (5.2).x²

   = 15x^{2 + 2} – 35.x^{2 + 1} + 10.x²

   = 15x⁴ – 35x³ + 10x².

   

   Bài 76 trang 33 Toán 8 Tập 1: Làm tính nhân:

   a) (2x² – 3x)(5x² – 2x + 1)

   b) (x – 2y)(3xy + 5y² + x)

   Lời giải:

   a) (2x² – 3x)(5x² – 2x + 1)

   = 2x²(5x² – 2x + 1) + (-3x)(5x² – 2x + 1)

   = 2x².5x² + 2x².(-2x) + 2x².1 + (–3x).5x² + (-3x).(-2x) + (-3x).1

   = (2.5)(x².x²) + [2. (-2)].(x².x) + 2x² + [(-3).5].(x.x²) + [(-3).(-2)].(x.x) + (-3x)

   = 10x⁴ – 4x³ + 2x² – 15x³ + 6x² – 3x

   = 10x⁴ – (4x³ + 15x³) + (2x² + 6x²) – 3x

   = 10x⁴ – 19x³ + 8x² – 3x

   b) (x – 2y)(3xy + 5y² + x)

   = x.(3xy + 5y² + x) + (-2y).(3xy + 5y² + x)

   = x.3xy + x.5y² + x.x + (-2y).3xy + (–2y).5y² + (–2y).x

   = 3x²y + 5xy² + x² – 6xy² – 10y³ – 2xy

   = 3x²y + (5xy² – 6xy²) + x² – 10y³ – 2xy

   = 3x²y – xy² + x² – 10y³ – 2xy

   Bài 77 trang 33 Toán 8 Tập 1: Tính nhanh giá trị của biểu thức:

   a) M = x² + 4y² – 4xy tại x = 18 và y = 4

   b) N = 8x³ – 12x²y + 6xy² – y³ tại x = 6 và y = – 8

   Lời giải:

   a) M = x² + 4y² – 4xy

   = x² – 2.x.2y + (2y)² (Hằng đẳng thức (2))

   = (x – 2y)²

   Thay x = 18, y = 4 vào biểu thức trên, ta được:

   M = (18 – 2.4)² = 10² = 100.

   Vậy giá trị biểu thức M tại x = 18 và y = 4 là: 100.

   b) N = 8x³ – 12x²y + 6xy² – y³

   = (2x)³ – 3(2x)²y + 3.2xy² – y³ (Hằng đẳng thức (5))

   = (2x – y)³

   Thay x = 6, y = – 8 ta được: N = (2.6 – (-8))³ = 20³ = 8000.

   Vậy giá trị biểu thức N tại x = 6 và y = -8 là 8000.

   Bài 78 trang 33 Toán 8 Tập 1: Rút gọn các biểu thức sau:

   a) (x + 2)(x – 2) – (x – 3)(x + 1)

   b) (2x + 1)² + (3x – 1)² + 2(2x + 1)(3x – 1)

   Lời giải:

   a) (x + 2)(x – 2) – (x – 3)(x + 1)

   = x² – 2² – (x² + x – 3x – 3)

   = x² – 4 – x² – x + 3x + 3

   = (x² – x²) + (-x + 3x) + (-4 + 3)

   = 2x – 1

   b) (2x + 1)² + (3x – 1)² + 2(2x + 1)(3x – 1)

   = (2x + 1)² + 2.(2x + 1)(3x – 1) + (3x – 1)²

   = [(2x + 1) + (3x – 1)]²

   = (2x + 1 + 3x – 1)²

   = [(2x + 3x) + (1 – 1)]²

   = (5x)²

   = 25x²

   Bài 79 trang 33 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

   a) x² – 4 + (x – 2)²

   b) x³ – 2x² + x – xy²

   c) x³ – 4x² – 12x + 27

   Lời giải:

   a) Cách 1: x² – 4 + (x – 2)²

   = (x²– 2²) + (x – 2)² (biểu thức trong ngoặc đầu tiên có dạng hằng đẳng thức số (3))

   = (x – 2)(x + 2) + (x – 2)² (Có nhân tử chung x – 2)

   = (x – 2)[(x + 2) + (x – 2)]

   = (x – 2)(x + 2 + x – 2)

   = (x – 2)(2x)

   = 2x(x – 2)

   Cách 2: x² – 4 + (x – 2)²   (Khai triển biểu thức trong ngoặc là hằng đẳng thức (2))

   = x² – 4 + (x² – 2.x.2 + 2²)

   = x² – 4 + x² – 4x + 4

   = 2x² – 4x (Có nhân tử chung là 2x)

   = 2x(x – 2)

   b) x³ – 2x² + x – xy² (Có nhân tử chung x)

   = x(x² – 2x + 1 – y²) (Có x² – 2x + 1 là hằng đẳng thức số (1))

   = x[(x – 1)² – y²] (biểu thức trong ngoặc vuông có dạng hằng đẳng thức số (3))

   = x(x – 1 + y)(x – 1 – y).

   c) x³ – 4x² – 12x + 27 (Sử dụng phương pháp nhóm hạng tử)

   = (x³ + 27) – (4x² + 12x)

   = (x³ + 3³) – (4x² + 12x) (nhóm 1 là HĐT số (6), nhóm 2 có 4x là nhân tử chung)

   = (x + 3)(x² – 3x + 9) – 4x(x + 3)

   = (x + 3)(x² – 3x + 9 – 4x)

   = (x + 3)(x² – 7x + 9)

   Bài 80 trang 33 Toán 8 Tập 1: Làm tính chia:

   a) (6x³ – 7x² – x + 2) : (2x + 1)

   b) (x⁴ – x³ + x² + 3x) : (x² – 2x + 3)

   c) (x² – y² + 6x + 9) : (x + y + 3)

   Lời giải:

   a) Cách 1:Thực hiện phép chia

   

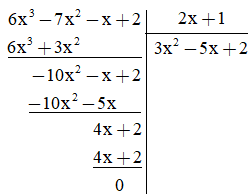
   Vậy (6x³ – 7x² – x + 2) : (2x + 1) = 3x² – 5x + 2.

   Cách 2: Phân tích 6x³ – 7x² – x + 2 thành (2x + 1).P(x) + R(x)

   6x³ – 7x² – x + 2

   = 6x³ + 3x² – 10x² – 5x + 4x + 2

   (Tách -7x² = 3x² – 10x²; -x = -5x + 4x)

   = (6x³ + 3x²) – (10x² + 5x) + (4x + 2)

   = 3x².(2x + 1) – 5x.(2x + 1) + 2.(2x + 1)

   = (3x² – 5x + 2)(2x + 1)

   Suy ra P(x) = 3x² – 5x + 2, R(x) = 0.

   Vậy (6x³ – 7x² – x + 2) : (2x + 1) = 3x² – 5x + 2

   Giải thích cách tách:

   Để xuất hiện nhân tử (2x + 1) với số hạng 6x³ ta cần thêm 3x² để có thể phân tích thành 3x²(2x + 1). Do đó ta tách -7x² = 3x² – 10x².

   Lại có -10x² nên ta cần thêm -5x để có thể phân tích thành -5x(2x + 1). Do đó ta tách –x = -5x + 4x.

   Có 4x, ta cần thêm 2 để có 2.(2x + 1) nên 2 không cần phải tách.

   b) Cách 1: Thực hiện phép chia

   

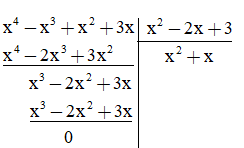
   Vậy (x⁴ – x³ + x² + 3x) : (x² – 2x + 3) = x² + x

   Cách 2: Phân tích x⁴ – x³ + x² + 3x thành nhân tử có chứa nhân tử x² – 2x + 3

   x⁴ – x³ + x² + 3x

   = x.(x³ – x² + x + 3)

   = x.(x³ – 2x² + 3x + x² – 2x + 3)

   = x.[x.(x² – 2x + 3) + (x² – 2x + 3)]

   = x.(x + 1)(x² – 2x + 3)

   Vậy (x⁴ – x³ + x² + 3x) : (x² – 2x + 3)

   = x(x + 1) = x² + x.

   c) Đa thức này không phải đa thức một biến đã sắp xếp nên ta không thực hiện cách chia trực tiếp được.

   Phân tích số bị chia thành nhân tử, trong đó có nhân tử là số chia.

   (x² – y² + 6x + 9) : (x + y + 3)

   (Có x² + 6x + 9 là hằng đẳng thức số (2))

   = (x² + 6x + 9 – y²) : (x + y + 3)

   = [(x² + 2.x.3 + 3²) – y²] : (x + y + 3)

   = [(x + 3)² – y²] : (x + y + 3)

   (biểu thức trong ngoặc vuông xuất hiện hằng đẳng thức số (3))

   = (x + 3 + y)(x + 3 – y) : (x + y + 3)

   = x + 3 – y = x – y + 3.

   Vậy (x² – y² + 6x + 9) : (x + y + 3) = x – y + 3

   Bài 81 trang 33 Toán 8 Tập 1: Tìm x, biết:

   a) $\frac{2}{3}x\left(x^2-4\right)=0;$

   b) (x + 2)² – (x – 2)(x + 2) = 0;

   c) $x+2\sqrt{2}{x}^2+2x^3=0.$

   Lời giải:

   a) $\frac{2}{3}x\left(x^2-4\right)=0$ (biểu thức trong ngoặc là hằng đẳng thức số (3))

   $\iff \frac{2}{3}x\left(x-2\right)\left(x+2\right)=0$ 

   $\iff \left[\begin{array}{l}\frac{2}{3}x=0\\ x-2=0\\ x+2=0\end{array}\right.\iff \left[\begin{array}{l}x=0\\ x=2\\ x=-2\end{array}\right.$

    Vậy $x\in \left\{0;-2;2\right\}.$

   b) (x + 2)² – (x – 2)(x + 2) = 0 (Có x + 2 là nhân tử chung)

   ⇔ (x + 2)[(x + 2) – (x – 2)] = 0

   ⇔ (x + 2)(x + 2 – x + 2) = 0

   ⇔ (x + 2).4 = 0

   ⇔ x + 2 = 0

   ⇔ x = – 2

   Vậy x = -2

   c) $x+2\sqrt{2}{x}^2+2x^3=0$ (có nhân tử chung là x)

   $\iff x\left(1+2\sqrt{2}x+2x^2\right)=0\iff x\left(2x^2+2\sqrt{2}x+1\right)=0$

   $\iff x\left[{\left(\sqrt{2}x\right)}^2+2.\sqrt{2}x.1+1\right]=0$ (biểu thức bên trong dấu ngoặc vuông là HĐT số (1))

   $\iff x.{\left(\sqrt{2}x+1\right)}^2=0\iff \left[\begin{array}{l}x=0\\ \sqrt{2}x+1=0\end{array}\right.\iff \left[\begin{array}{l}x=0\\ x=-\frac{1}{\sqrt{2}}\end{array}\right.$

   Vậy $x\in \left\{0;-\frac{1}{\sqrt{2}}\right\}.$

   Bài 82 trang 33 Toán 8 Tập 1: Chứng minh:

   a) x² – 2xy + y² + 1 > 0 với mọi số thực x và y.

   b) x – x² – 1 < 0 với mọi số thực x.

   Lời giải:

   a) Ta có: x² – 2xy + y² + 1

   = (x² – 2xy + y²) + 1

   = (x – y)² + 1.

   Vì ${\left(x-y\right)}^2\ge 0$ với mọi x, y thuộc R

    với mọi số thực x, y

   b) Ta có: $x-x^2-1$

   

   Ta có: ${\left(x-\frac{1}{2}\right)}^2\ge 0$ với mọi số thực x

   $\Rightarrow {\left(x-\frac{1}{2}\right)}^2+\frac{3}{4}\ge 0+\frac{3}{4}>0$ với mọi số thực x

   $\Rightarrow -\left[{\left(x-\frac{1}{2}\right)}^2+\frac{3}{4}\right]<0$ với mọi số thực x hay $x-x^2-1<0$ với mọi số thực x (ĐPCM).

   Bài 83 trang 33 Toán 8 Tập 1: Tìm $n\in \mathbb{Z}$ để 2n² – n + 2 chia hết cho 2n + 1.

   Lời giải:

   Thực hiện phép chia 2n² – n + 2 cho 2n + 1 ta có:

   

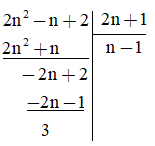
   Để 2n² – n + 2 chia hết cho 2n + 1

   $\iff 3⋮\left(2n+1\right)$ hay (2n + 1)  Ư(3) = {-3; -1; 1; 3}.

   $\iff 2n+1\in \left\{-3;-1;1;3\right\}$

   Ta có bảng sau:

   2n + 1	-3	-1	1	3
   n	-2	-1	0	1

   Vậy $n\in \left\{-2;-1;0;1\right\}$

3. Sách bài tập Toán 6 (Kết nối tri thức) Ôn tập chương 1 trang 28, 29

   Giải SBT Toán lớp 6 Ôn tập chương 1 trang 28, 29

   Câu hỏi (Trắc Nghiệm)

   Bài 1 trang 28 sách bài tập Toán lớp 6 Tập 1: Tập hợp các chữ cái trong cụm từ LÀO CAI là:

   (A) {LÀO; CAI};

   (B) {L; À; O; C; A; I}

   (C) {L; A; O; C; A; I}

   (D) {L; A; O; C; I}

   Lời giải:

   Các chữ cái trong từ “LÀO CAI” gồm L, A, O, C, A, I.

   Trong các chữ cái trên, chữ A được xuất hiện 2 lần nhưng ta chỉ viết mỗi chữ một lần, ta có tập hợp các chữ cái {L; A; O; C; I}

   Đáp án cần chọn là: D

   Bài 2 trang 28 sách bài tập Toán lớp 6 Tập 1: Trong các chữ số của số 19 254;

   (A) Giá trị của chữ số 2 bằng nửa giá trị của chữ số 4;

   (B) Giá trị của chữ số 2 bằng 5 lần giá trị của chữ số 4;

   (C) Giá trị của chữ số 2 bằng 50 lần giá trị của chữ số 4;

   (D) Giá trị của chữ số 2 bằng 500 lần giá trị của chữ số 4;

   Lời giải:

   +) Ta thấy số 19 254 có chữ số 2 đứng ở hàng trăm nên có giá trị là 2. 100 = 200

   +) Ta thấy số 19 254 có chữ số 4 đứng ở hàng đơn vị nên có giá trị là 4. 1 = 4

   Ta có: 200: 4 = 50

   Do đó giá trị của chữ số 2 bằng 50 lần giá trị của chữ số 4

   Đáp án cần chọn là: C

   Bài 3 trang 28 sách bài tập Toán lớp 6 Tập 1: Viết số a = 24 053 thành tổng giá trị các chữ số của nó. Kết quả là:

   (A) a = 24 000 + 50 + 3;

   (B) a = 20 000 + 4 000 + 53

   (C) a = 20 000 + 4 000 + 50 + 3

   (D) a = 20 000 + 4 050 + 3

   Lời giải:

   Số a = 24 053 có:

   +) Chữ số 2 nằm ở hàng chục nghìn và có giá trị bằng 2 x 10 000 = 20 000

   +) Chữ số 4 nằm ở hàng nghìn và có giá trị bằng 4 x 1 000 = 4 000

   +) Chữ số 0 nằm ở hàng trăm và có giá trị bằng 0 x 100 = 0

   +) Chữ số 5 nằm ở hàng chục và có giá trị bằng 5 x 10 = 50

   +) Chữ số 3 nằm ở hàng đơn vị và có giá trị bằng 3 x 1 = 3

   Vậy a = 20 000 + 4 000 + 50 + 3

   Đáp án cần chọn là: C

   Bài 4 trang 28 sách bài tập Toán lớp 6 Tập 1: Cho m ∈ N*. Ba số tự nhiên liên tiếp tăng dần là:

   (A) m – 2, m – 1, m;           (B) m – 1, m, m + 1;

   (C) m + 1, m, m -1;            (D) m, m – 1, m – 2 

   Lời giải:

   +) Ta thấy m + 1 > m nên (C) sai vì sắp xếp theo theo thứ tự tăng dần

   +) Ta cũng có m > m – 1 nên (D) sai vì sắp xếp theo theo thứ tự tăng dần

   Vì m ∈ N* nên m nhỏ nhất là 1, vì thế mà m – 2 không thực hiện được nên (A) sai

   Đáp án cần chọn là: B

   Bài 5 trang 28 sách bài tập Toán lớp 6 Tập 1: Cho tập hợp P (H.1.5). Trong các câu sau đây, câu nào sai?

   (A) P = {0; 1; 2; 3; 4; 5}

   (B) P = { x ∈ N | x ≤ 5}

   (C) P = { x ∈ N | x < 6}

   (D) P = { x ∈ N | x < 5}

   

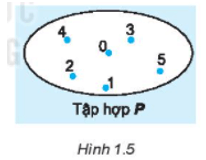
   Lời giải:

   Trong hình 1.5, tập hợp P có các phần tử thuộc tập hợp là: 0; 1; 2; 3; 4; 5 (các số này đều nằm trong vòng kín biểu diễn tập hợp P).

   + Ta viết tập hợp P bằng cách liệt kê các phần tử là: P = {0; 1; 2; 3; 4; 5} nên đáp án A đúng.

   + Vì các số 0; 1; 2; 3; 4; 5 là các số tự nhiên nhỏ hơn 6 (hoặc nhỏ hơn hoặc bằng 5).

   + Do đó bằng cách nêu dấu hiệu đặc trưng ta viết P = { x ∈ ℕ | x < 6} hoặc P = {x ∈ ℕ | x ≤ 5} nên đáp án B và C đúng.

   + Ở đáp án D, viết P = { x ∈ ℕ | x < 5} có nghĩa tập hợp P chứa các phần tử nhỏ hơn 5. Do đó phần tử 5 không thuộc tập hợp P.

   Vậy D sai.

   Đáp án cần chọn là: D

   Bài 6 trang 28 sách bài tập Toán lớp 6 Tập 1: Xét tập hợp A = { x ∈ N | x ≤ 7}. Trong các số sau đây, số nào không thuộc tập A?

   (A) 0;                (B) 5; 

   (C) 7                (D) 11.

   Lời giải:

   A = { x ∈ N | x ≤ 7}. Tập hợp A bao gồm các số tự nhiên nhỏ hơn hoặc bằng 7 là: 0; 1; 2; 3; 4; 5; 6; 7.

   Do vậy 11 ∉ A .

   Đáp án cần chọn là: D

   Bài 7 trang 28 sách bài tập Toán lớp 6 Tập 1: Câu nào trong các câu sau đây là câu đúng?

   (A) Phép chia 687 cho 18 có số dư là 3;

   (B) Phép chia 2 048 cho 128 có thương là 0;

   (C) Phép chia 9 845 cho 125 có số dư là 130;

   (D) Phép chia 295 cho 5 có thương là 300.

   Lời giải:

   Xét (A)

   

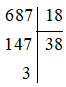
   Vậy 687: 18 có số dư là 3 nên đáp án A đúng.

   Kiểm tra cho (B), (C), (D) đều sai.

   Đáp án cần chọn là: A

   Bài 8 trang 29 sách bài tập Toán lớp 6 Tập 1: Lũy thừa với số mũ tự nhiên có tính chất nào sau đây?

   (A) a^m.aⁿ = a^mn                                        (B) a^m : aⁿ = a^m:n

   (C) a^m.aⁿ = a^m+n                                      (D) a^m.aⁿ = a^m-n

   Lời giải:

   Lũy thừa với số mũ tự nhiên có tính chất a^m.aⁿ = a^m+n và a^m : aⁿ = a^m-n. Vậy đáp án C đúng.

   Đáp án cần chọn là: C

   Bài 9 trang 29 sách bài tập Toán lớp 6 Tập 1: Lũy thừa 10⁹ nhận giá trị nào sau đây?

   (A) 100 000;                     (B) 1 000 000 000

   (C) 1 000 000;                  (D) 10 000 000 000

   Lời giải:

   Ta có: 10⁹ = 1 000 000 000 

   Đáp án cần chọn là: B

   Bài tập

   Bài 1.68 trang 29 sách bài tập Toán lớp 6 Tập 1: Gọi P là tập hợp các số tự nhiên lẻ, lớn hơn 3 nhưng không lớn hơn 9.

   a) Mô tả tập hợp P bằng hai cách;

   b) Biểu diễn các phần tử của tập P trên cùng một tia số.

   Lời giải:

   a) Các số tự nhiên lẻ lớn hơn 3 nhưng không lớn hơn 9 (nghĩa là nhỏ hơn hoặc bằng 9) là: 5; 7; 9

   P là tập hợp các số tự nhiên lẻ, lớn hơn 3 nhưng không lớn hơn 9, do đó ta viết tập hợp P bằng hai cách như sau:

   +) Cách 1: P = {5; 7; 9}

   +) Cách 2: P = { x ∈ N| x lẻ và 3 < x ≤ 9}

   b) Biểu diễn các phần tử P trên cùng một tia số là:

   Gọi điểm A biểu diễn số 5, điểm B biểu diễn số 7 và điểm C biểu diễn số 9.

   

   Bài 1.69 trang 29 sách bài tập Toán lớp 6 Tập 1: Một số có hai chữ số, trong đó hiệu của chữ số hàng đơn vị và chữ số hàng chục bằng 8. Hỏi số đó là số nào?

   Lời giải:

   Vì hiệu của chữ số hàng đơn vị và chữ số hàng chục bằng 8, do đó chữ số hàng đơn vị phải lớn hơn hoặc bằng 8.

   +) Với chữ số hàng đơn vị là 8 thì chữ số hàng chục là: 8 – 8 = 0 (loại) vì chữ số hàng chục đứng đầu nên phải khác 0.

   +) Với chữ số hàng đơn vị là 9 thì chữ số hàng chục là: 9 – 8 = 1 (thỏa mãn)

   Vậy số cần tìm là 19.

   Bài 1.70 trang 29 sách bài tập Toán lớp 6 Tập 1: Tìm các số tự nhiên lẻ có ba chữ số mà tổng các chữ số của nó bằng 5.

   Lời giải:

   Phân tích 5 thành tổng của ba chữ số, ta có:

   5 = 0 + 0 + 5 = 0 + 1 + 4 = 0 + 2 + 3 = 1 + 1 + 3 = 1 + 2 + 2

   Trường hợp 1: 5 = 0 + 0 + 5, ta được số 500 (loại vì 500 không phải là số lẻ)

   Trường hợp 2: 5 = 0 + 1 + 4, vì số cần tìm là số lẻ, mà chữ số hàng trăm khác 0 nên số cần tìm là 401.

   Trường hợp 3: 5 = 0 + 2 + 3, ta được số lẻ là 203

   Trường hợp 4: 5 = 1 + 1 + 3, ta được các số lẻ là 113; 131; 311

   Trường hợp 5: 5 = 1 + 2 + 2, ta được số lẻ 221.

   Vậy các số cần tìm là: 401; 203; 113; 131; 311; 221.

   Bài 1.71 trang 29 sách bài tập Toán lớp 6 Tập 1: Tìm các số tự nhiên chẵn có ba chữ số mà tổng các chữ số của nó bằng 5.

   Lời giải:

   Phân tích 5 thành tổng của ba chữ số, ta có:

   5 = 0 + 0 + 5 = 0 + 1 + 4 = 0 + 2 + 3 = 1 + 1 + 3 = 1 + 2 + 2

   Trường hợp 1: 5 = 0 + 0 + 5, ta được số chẵn là 500 

   Trường hợp 2: 5 = 0 + 1 + 4, ta được số chẵn là 104; 140; 410

   Trường hợp 3: 5 = 0 + 2 + 3, ta được số chẵn là 230; 320; 302

   Trường hợp 4: 5 = 1 + 1 + 3, không có số chẵn 

   Trường hợp 5: 5 = 1 + 2 + 2, ta được số chẵn là 122; 212

   Vậy các số cần tìm là: 500; 104; 140; 410; 230; 320; 302; 122; 212.

   Bài 1.72 trang 29 sách bài tập Toán lớp 6 Tập 1: Xét tập E gồm các số tự nhiên, mỗi số đều có năm chữ số xếp theo thứ tự không giảm và tập các chữ số của nó là {1; 3; 5; 7}.

   a) Mô tả tập E bằng cách liệt kê các phần tử của nó.

   b) Gọi n là số lớn nhất trong tập E. Biểu diễn n thành tổng giá trị các chữ số của nó.

   Lời giải:

   a) Vì các số thuộc tập E có năm chữ số, trong khi tập các chữ số của chúng chỉ có bốn chữ số nên phải có một chữ số xuất hiện 2 lần.

   +) Với chữ số 1 xuất hiện 2 lần ta được số sắp xếp theo thứ tự không giảm là: 11 357

   +) Với chữ số 3 xuất hiện 2 lần ta được số sắp xếp theo thứ tự không giảm là: 13 357

   +) Với chữ số 5 xuất hiện 2 lần ta được số sắp xếp theo thứ tự không giảm là: 13 557

   +) Với chữ số 7 xuất hiện 2 lần ta được số sắp xếp theo thứ tự không giảm là: 13 577

   Vậy E = {11 357; 13 357; 13 557; 13 577}

   b) Vì 11 357 < 13 357 < 13 557 < 13 577 nên 13 577 là số lớn nhất của tập E.

   Vì n là số lớn nhất trong tập E nên n = 13 577

   + Chữ số 1 nằm ở hàng chục nghìn và có giá trị bằng 1 x 10 000 

   +) Chữ số 3 nằm ở hàng nghìn và có giá trị bằng 3 x 1 000 

   +) Chữ số 5 nằm ở hàng trăm và có giá trị bằng 5 x 100 

   +) Chữ số 7 nằm ở hàng chục và có giá trị bằng 7 x 10 

   +) Chữ số 7 nằm ở hàng đơn vị và có giá trị bằng 7 x 1

   Do đó biểu diễn n thành tổng các giá trị của nó là: 

   13 577 = 1 x 10 000 + 3 x 1 000 + 5 x 100 + 7 x 10 + 7 x 1

   Bài 1.73 trang 29 sách bài tập Toán lớp 6 Tập 1: Có bao nhiêu số có hai chữ số trong đó có mặt chữ số 2?

   Lời giải:

   Các số có hai chữ số trong đó có mặt chữ số 2 là: 20; 21; 22; 23; 24; 25; 26; 27; 28; 29; 12; 32; 42; 52; 62; 72; 82; 92.

   Vậy có 18 số có hai chữ số trong đó có mặt chữ số 2.

   Bài 1.74 trang 29 sách bài tập Toán lớp 6 Tập 1: Lớp 6A có 42 học sinh. Trong đợt thi đua lập thành tích chào mừng Ngày Nhà giáo Việt Nam (20/11), học sinh nào trong lớp cũng được ít nhất một điểm 10. Hãy cho biết trong đợt thi đua đó, lớp 6A được tất cả bao nhiêu điểm 10, biết rằng trong lớp có 39 bạn được từ hai điểm 10 trở lên, 14 bạn được ba điểm 10 trở lên, 5 bạn được bốn điểm 10 và không ai được hơn bốn điểm 10.

   Lời giải:

   Số bạn được đúng một điểm 10 là:

   42 – 39 = 3 (bạn)

   Số bạn được đúng hai điểm 10 là:

   39 – 14 = 25 (bạn)

   Số bạn được đúng ba điểm 10 là:

   14 – 5 = 9 (bạn)

   Số bạn được đúng bốn điểm 10 là 5.

   Tổng số điểm 10 của cả lớp 6A là:

   3. 1 + 25. 2 + 9. 3 + 5. 4 = 100 (điểm 10)

   Vậy lớp 6A được tất cả 100 điểm 10.

   Bài 1.75 trang 29 sách bài tập Toán lớp 6 Tập 1: Khi đặt tính nhân để tính tích a. 254, bạn Quang đã viết các tích riêng thẳng cột: chữ số hàng đơn vị dưới chữ số hàng đơn vị; chữ số hàng chục dưới chữ số hàng chục; … nên nhận được kết quả là 13 783. Nếu đặt tính đúng thì kết quả phải bằng bao nhiêu?

   Lời giải:

   Bạn Quang đã viết các tích riêng thẳng cột: chữ số hàng đơn vị dưới chữ số hàng đơn vị; chữ số hàng chục dưới chữ số hàng chục; … Do đặt sai vị trí các tích riêng nên 13 783 là tổng các tích riêng.

   Ta có tổng các tích riêng là: 

   a. 2 + a. 5 + a. 4 = a. (2 + 5 + 4) = a. 11. 

   Do đó: a. 11 = 13 783

   Suy ra a = 13 783: 11 = 1 253

   Tích đúng là 1 253. 254 

   

   Vậy tích đúng là 1 253. 254 = 318 262.

   Bài 1.76 trang 29 sách bài tập Toán lớp 6 Tập 1: Tính S = 1 + 2 – 3 – 4 + 5 + 6 – 7 – 8 + 9 + 10 – … + 2 018 – 2 019 – 2 020 + 2 021

   Lời giải:

   S = 1 + 2 – 3 – 4 + 5 + 6 – 7 – 8 + 9 + 10 – … + 2 018 – 2 019 – 2 020 + 2 021

   = 1 + (2 – 3 – 4 + 5) + (6 – 7 – 8 + 9) + … + (2 018 – 2 019 – 2 020 + 2 021)

   = 1 + [(5 + 2) – (3 + 4)] + [(6 + 9) – (7 + 8)] + … + [(2 018 + 2 021) – (2 019 + 2 020)]

   = 1 + (7 – 7) + (15 – 15) + … + (4 039 – 4 039)

   = 1 + 0 + 0 + … + 0

   = 1.

   Bài 1.77 trang 29 sách bài tập Toán lớp 6 Tập 1: Trong một phép chia, số bị chia là 89, số dư là 12. Tìm số chia và thương.

   Lời giải:

   Gọi số chia và thương lần lượt là b và q (b; q ∈ ℕ, b ≠0).

   Như vậy 89 : b = q (dư 12) và b > 12 (số chia lớn hơn số dư).

   Từ đó 89 = bq + 12. Suy ra bq = 89 – 12 = 77 = 7 . 11 = 77 . 1

   Mà b > 12 nên b = 77 và q = 1.

   Do đó 89 : 77 = 1 (dư 12).

   Vậy số chia bằng 77, thương bằng 1.

4. 20 câu Trắc nghiệm Công nghệ 10 Chương 1 (Kết nối tri thức 2023) có đáp án: Đại cương về công nghệ

   Trắc nghiệm Công nghệ 10 Chương 1: Đại cương về công nghệ

   Câu 1. Công nghệ thứ tư trong lĩnh vực luyện kim được đề cập đến là:

   A. Công nghệ luyện kim

   B. Công nghệ đúc

   C. Công nghệ gia công cắt gọt

   D. Công nghệ gia công áp lực

   Hướng dẫn giải

   Đáp án đúng: D

   Giải thích: Có 5 công nghệ phổ biến trong lĩnh vực luyện kim, cơ khí:

   1. Công nghệ luyện kim

   2. Công nghệ đúc

   3. Công nghệ gia công cắt gọt

   4. Công nghệ gia công áp lực

   5. Công nghệ hàn

   Câu 2. Công nghệ thứ năm trong lĩnh vực luyện kim được đề cập đến là:

   A. Công nghệ hàn

   B. Công nghệ đúc

   C. Công nghệ gia công cắt gọt

   D. Công nghệ gia công áp lực

   Hướng dẫn giải

   Đáp án đúng: A

   Giải thích: Có 5 công nghệ phổ biến trong lĩnh vực luyện kim, cơ khí:

   1. Công nghệ luyện kim

   2. Công nghệ đúc

   3. Công nghệ gia công cắt gọt

   4. Công nghệ gia công áp lực

   5. Công nghệ hàn

   Câu 3. Công nghệ hàn là gì?

   A. Là công nghệ nối các chi tiết bằng kim loại với nhau thành một khối không thể tháo rời được bằng cách nung nóng chỗ nối đến trạng thái hàn.

   B. Là công nghệ chế tạo sản phẩm kim loại bằng phương pháp nấu kim loại thành trạng thái lỏng, sau đó rót vào khuôn có hình dạng và kích thước như sản phẩm.

   C. Là công nghệ thực hiện việc lấy đi một phần kim loại của phôi dưới dạng phoi nhờ các dụng cụ cắt và máy cắt kim loại để tạo ra chi tiết có hình dạng, kích thước theo yêu cầu.

   D. Là công nghệ dựa vào tính dẻo của kim loại, dùng ngoại lực của thiết bị làm cho kim loại biến dạng theo hình dáng yêu cầu

   Hướng dẫn giải

   Đáp án đúng: A

   Giải thích:

   + Đáp án A: Công nghệ hàn

   + Đáp án B: Công nghệ đúc

   + Đáp án C: Công nghệ gia công cắt gọt

   + Đáp án D: Công nghệ gia công áp lực

   Câu 4. Công nghệ thứ năm trong lĩnh vực điện – điện tử được đề cập đến là:

   A. Công nghệ sản xuất điện năng

   B. Công nghệ điện – quang

   C. Công nghệ điện – cơ

   D. Công nghệ truyền thông không dây

   Hướng dẫn giải

   Đáp án đúng: D

   Giải thích:

   Có 5 công nghệ trong lĩnh vực điện – điện tử:

   1. Công nghệ sản xuất điện năng

   2. Công nghệ điện – quang

   3. Công nghệ điện – cơ

   4. Công nghệ điều khiển và tự động hóa

   5. Công nghệ truyền thông không dây

   Câu 5. Công nghệ mới thứ năm được giới thiệu là:

   A. Công nghệ năng lượng tái tạo

   B. Công nghệ trí tuệ nhân tạo

   C. Công nghệ internet vạn vật

   D. Công nghệ robot thông minh

   Hướng dẫn giải

   Đáp án đúng: B

   Giải thích: Có 7 công nghệ mới được giới thiệu trong chương trình:

   1. Công nghệ nano

   2. Công nghệ CAD/CAM/CNC

   3. Công nghệ in 3D

   4. Công nghệ năng lượng tái tạo

   5. Công nghệ trí tuệ nhân tạo

   6. Công nghệ internet vạn vật

   7. Công nghệ robot thông minh

   Câu 6. Hình ảnh nào sau đây thể hiện phương pháp thủy canh?

   A. 

   B. 

   C. 

   D. Cả 3 đáp án trên

   Hướng dẫn giải

   Đáp án đúng: B

   Giải thích:

   + Hình A: phương pháp địa canh

   + Hình B: phương pháp thủy canh

   + Hình C: phương pháp khí canh

   Câu 7. Hình ảnh nào sau đây thể hiện phương pháp khí canh?

   A. 

   B. 

   C. 

   D. Cả 3 đáp án trên

   Hướng dẫn giải

   Đáp án đúng: C

   Giải thích:

   + Hình A: phương pháp địa canh

   + Hình B: phương pháp thủy canh

   + Hình C: phương pháp khí canh

   Câu 8. Mối quan hệ đầu tiên giữa khoa học, kĩ thuật và công nghệ được đề cập đến là:

   A. Khoa học là cơ sở của kĩ thuật

   B. Kĩ thuật tạo ra công nghệ mới, dựa trên công nghệ hiện có

   C. Công nghệ thúc đẩy khoa học

   D. Cả 3 đáp án trên

   Hướng dẫn giải

   Đáp án đúng: A

   Giải thích: Quan hệ giữa khoa học, kĩ thuật và công nghệ thể hiện ở 3 đặc điểm:

   1. Khoa học là cơ sở của kĩ thuật

   2. Kĩ thuật tạo ra công nghệ mới, dựa trên công nghệ hiện có

   3. Công nghệ thúc đẩy khoa học

   Câu 9. Mối quan hệ thứ hai giữa khoa học, kĩ thuật và công nghệ được đề cập đến là:

   A. Khoa học là cơ sở của kĩ thuật

   B. Kĩ thuật tạo ra công nghệ mới, dựa trên công nghệ hiện có

   C. Công nghệ thúc đẩy khoa học

   D. Cả 3 đáp án trên

   Hướng dẫn giải

   Đáp án đúng: B

   Giải thích: Quan hệ giữa khoa học, kĩ thuật và công nghệ thể hiện ở 3 đặc điểm:

   1. Khoa học là cơ sở của kĩ thuật

   2. Kĩ thuật tạo ra công nghệ mới, dựa trên công nghệ hiện có

   3. Công nghệ thúc đẩy khoa học

   Câu 10. Mối quan hệ thứ ba giữa khoa học, kĩ thuật và công nghệ được đề cập đến là:

   A. Khoa học là cơ sở của kĩ thuật

   B. Kĩ thuật tạo ra công nghệ mới, dựa trên công nghệ hiện có

   C. Công nghệ thúc đẩy khoa học

   D. Cả 3 đáp án trên

   Hướng dẫn giải

   Đáp án đúng: C

   Giải thích: Quan hệ giữa khoa học, kĩ thuật và công nghệ thể hiện ở 3 đặc điểm:

   1. Khoa học là cơ sở của kĩ thuật

   2. Kĩ thuật tạo ra công nghệ mới, dựa trên công nghệ hiện có

   3. Công nghệ thúc đẩy khoa học

   Câu 11. Công nghệ mới thứ sáu được giới thiệu là:

   A. Công nghệ năng lượng tái tạo

   B. Công nghệ trí tuệ nhân tạo

   C. Công nghệ internet vạn vật

   D. Công nghệ robot thông minh

   Hướng dẫn giải

   Đáp án đúng: C

   Giải thích: Có 7 công nghệ mới được giới thiệu trong chương trình:

   1. Công nghệ nano

   2. Công nghệ CAD/CAM/CNC

   3. Công nghệ in 3D

   4. Công nghệ năng lượng tái tạo

   5. Công nghệ trí tuệ nhân tạo

   6. Công nghệ internet vạn vật

   7. Công nghệ robot thông minh

   Câu 12. Công nghệ mới thứ bảy được giới thiệu là:

   A. Công nghệ năng lượng tái tạo

   B. Công nghệ trí tuệ nhân tạo

   C. Công nghệ internet vạn vật

   D. Công nghệ robot thông minh

   Hướng dẫn giải

   Đáp án đúng: D

   Giải thích: Có 7 công nghệ mới được giới thiệu trong chương trình:

   1. Công nghệ nano

   2. Công nghệ CAD/CAM/CNC

   3. Công nghệ in 3D

   4. Công nghệ năng lượng tái tạo

   5. Công nghệ trí tuệ nhân tạo

   6. Công nghệ internet vạn vật

   7. Công nghệ robot thông minh

   Câu 13. Tiêu chí thứ tư của đánh giá sản phẩm công nghệ là:

   A. Cấu tạo sản phẩm

   B. Tính năng sản phẩm

   C. Độ bền sản phẩm

   D. Tính thẩm mĩ sản phẩm

   Hướng dẫn giải

   Đáp án đúng: D

   Giải thích: Có 6 tiêu chí đánh giá sản phẩm công nghệ:

   1. Cấu tạo sản phẩm

   2. Tính năng sản phẩm

   3. Độ bền sản phẩm

   4. Tính thẩm mĩ sản phẩm

   5. Giá thành sản phẩm

   6. Tác động đến môi trường của sản phẩm

   Câu 14. Tiêu chí thứ năm của đánh giá sản phẩm công nghệ là:

   A. Giá thành sản phẩm

   B. Tính năng sản phẩm

   C. Độ bền sản phẩm

   D. Tính thẩm mĩ sản phẩm

   Hướng dẫn giải

   Đáp án đúng: A

   Giải thích: Có 6 tiêu chí đánh giá sản phẩm công nghệ:

   1. Cấu tạo sản phẩm

   2. Tính năng sản phẩm

   3. Độ bền sản phẩm

   4. Tính thẩm mĩ sản phẩm

   5. Giá thành sản phẩm

   6. Tác động đến môi trường của sản phẩm

   Câu 15. Bộ phận xử lí của hệ thống kĩ thuật có nhiệm vụ:

   A. Biến đổi

   B. Vận chuyển

   C. Lưu trữ vật liệu

   D. Cả 3 đáp án trên

   Hướng dẫn giải

   Đáp án đúng: D

   Giải thích: Cấu trúc hệ thống kĩ thuật có:

   – Đầu vào: vật liệu, năng lượng, thông tin cần xử lí

   – Đầu ra: vật liệu, năng lượng, thông tin đã xử lí

   – Bộ phận xử lí: biến đổi, vận chuyển, lưu trữ vật liệu, năng lượng, thông tin

   Xem thêm các bài trắc nghiệm Công nghệ 10 Kết nối tri thức hay, chi tiết khác:

   Trắc nghiệm Công nghệ 10 Bài 7: Ngành nghề kĩ thuật, công nghệ

   Trắc nghiệm Công nghệ 10 Ôn tập Chương 1: Đại cương về công nghệ

   Trắc nghiệm Công nghệ 10 Bài 8: Bản vẽ kĩ thuật và tiêu chuẩn trình bày bản vẽ kĩ thuật

   Trắc nghiệm Công nghệ 10 Bài 9: Hình chiếu vuông góc

   Trắc nghiệm Công nghệ 10 Bài 10: Mặt cắt hình cắt

   Trắc nghiệm Công nghệ 10 Bài 11: Hình chiếu trục đo

5. Giải SGK Sinh học 10 (Chân trời sáng tạo) Ôn tập chương 1

   Giải bài tập Sinh học lớp 10 Ôn tập chương 1

   Bài tập

   Giải Sinh học 10 trang 37

   Bài 1 trang 37 Sinh học 10: Vào mùa lạnh, thời tiết hanh, khô người ta thường bôi kem chống nẻ vào môi, gót chân để tránh bị nứt nẻ. Hãy giải thích cơ sở cho hiện tượng trên.

   Phương pháp giải:

    Lipid không tan trong nước (do trong cấu trúc chứa nhiều liên kết C-H không phân cực) nhưng tan trong các dung môi hữu cơ.

   Trả lời:

     Vào mùa lạnh, thời tiết hanh, cơ thể dễ bị thoát hơi nước ra ngoài môi trường, làm cho da chúng ta dễ bị nứt nẻ. Do đó người ta bôi kem chống nẻ vào môi, gót chân vì kem có bản chất là lipid, không tan trong nước nên có thể ngăn nước thoát từ các tế bào da.

   Bài 2 trang 37 Sinh học 10: Một bạn học sinh phát biểu rằng: “Nếu không có nước sẽ không có sự sống”. Em có đồng tình với ý kiến của bạn đó không? Tại sao?

   Phương pháp giải:

    Nước có nhiều vai trò quan trọng đối với tế bào: là thành phần chính cấu tạo nên tế bào, là dung môi hoà tan nhiều chất cần thiết, vừa là nguyên liệu vừa là môi trường cho nhiều phản ứng sinh hoá xảy ra trong tế bào để duy trì sự sống. Ngoài ra, nước còn đóng vai trò quan trọng trong việc đảm bảo sự cân bằng và ổn định nhiệt độ của tế bào và cơ thể.

   Trả lời:

    Em đồng tình với ý kiến của bạn vì nước có nhiều vai trò quan trọng đối với tế bào, do đó, nếu không có nước thì hầu như các phản ứng hóa sinh trong tế bào không diễn ra được.

   Bài 3 trang 37 Sinh học 10: Một nông dân nói rằng: “Khi nuôi lợn, nếu cho chúng ăn bã đậu hoặc khô dầu đậu tương thì tỉ lệ nạc sẽ cao hơn so với các loại thức ăn thông thường”. Hãy giải thích hiện tượng trên.

   Phương pháp giải:

    Protein có nhiều trong các loại hạt có dầu như đậu nành, đậu phộng (lạc),…. nên được sử dụng làm thực phẩm trong chăn nuôi.

   Trả lời:

    Bã đậu, khô dầu lạc là các phụ phẩm có chứa hàm lượng protein cao, nên khi các vật nuôi ăn bã đậu và khô dầu đậu sẽ được cung cấp nhiều protein, làm tỉ lệ nạc của gia súc cao hơn so với ăn các loại thức ăn thông thường.

   Bài 4 trang 37 Sinh học 10: Đối với các bệnh nhân bị tiêu chảy nặng, bác sĩ thường chỉ định truyền dịch cho họ. Dịch được truyền cho các bệnh nhân này có thành phần chủ yếu là gì? Việc truyền dịch có vai trò gì?

   Phương pháp giải:

   – Nhóm nguyên tố đa lượng: O, C, H, N, Ca, P, K, S, Na, Cl, Mg,… Các nguyên tố đại lượng tham gia cấu tạo nên các đại phân tử hữu cơ như prôtêin, cacbohidrat, lipit và các acid nucleic là những chất hóa học chính cấu tạo nên tế bào.

   – Nhóm nguyên tố vi lượng: Fe, I, Mo, Zn, Cu,…Các nguyên tố vi lượng là những nguyên tố chỉ chiếm tỉ lệ nhỏ hơn 0.01% khối lượng cơ thể sống, nhưng lại đóng 1 vai trò vô cùng quan trọng đối với hoạt động sống của cơ thể.

   Trả lời:

    Khi bị tiêu chảy nặng sẽ làm cơ thể mất nước rất nhiều, do đó các bệnh nhân bị tiêu chảy nặng thường được truyền dịch chứa thành phần chủ yếu là các chất điện giải để bổ sung lại lượng nước thiếu hụt trong cơ thể người bệnh.

   Bài 5 trang 37 Sinh học 10: Hãy sưu tầm tranh ảnh về một số loại tế bào ở người (tế bào biểu mô ruột non, tế bào hồng cầu, tế bào cơ,…). Nhận xét và giải thích về sự khác nhau giữa các tế bào đó.

   Phương pháp giải:

   Em có thể tìm kiếm hình ảnh trên các phương tiện như sách bào, internet,….

   Trả lời:

   

   

   

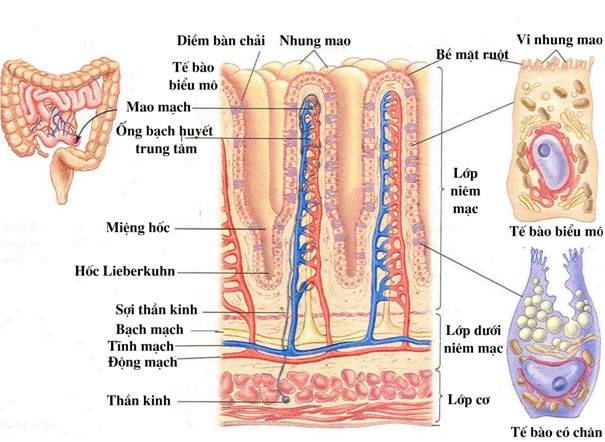
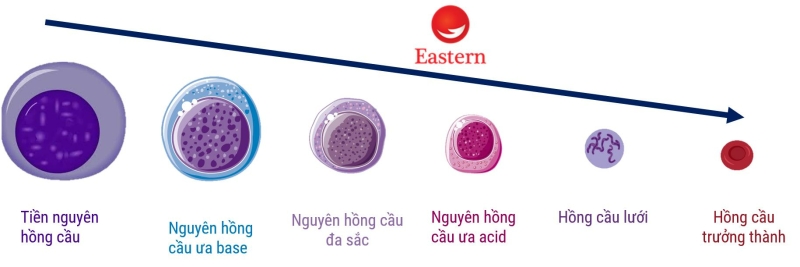
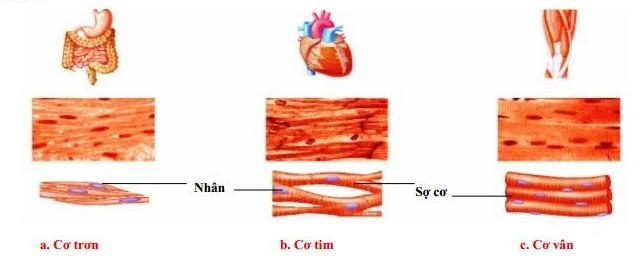
   Xem thêm các bài giải SGK Sinh học lớp 10 Chân trời sáng tạo hay, chi tiết khác:

   Bài 7: Thực hành: Xác định một số thành phần hóa học của tế bào

   Bài 8: Tế bào nhân sơ

   Bài 9: Tế bào nhân thực

   Bài 10: Thực hành: Quan sát tế bào