Một hình trụ có bán kính đáy là 3cm. Biết diện tích toàn phần của hình trụ gấp đôi diện tích xung quanh. Tính chiều cao của hình trụ

Câu hỏi:

Một hình trụ có bán kính đáy là 3cm. Biết diện tích toàn phần của hình trụ gấp đôi diện tích xung quanh. Tính chiều cao của hình trụ

Trả lời:

Diện tích toàn phần gấp đôi diện tích xung quanh nên:2πRh + 2π$R^2$ = 2.2π$R^2$ => 2πRh = 2π$R^2$ => R = hVậy chiều cao của hình trụ là 3cm

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Lý thuyết Diện tích xung quanh của hình chóp đều (mới 2023) – Toán 8

   Lý thuyết Diện tích xung quanh của hình chóp đều

   1. Công thức tính diện tích của hình chóp đều

   a) Diện tích xung quanh của hình chóp đều

   Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn:

   S_xq = p.d    (p: nửa chu vi đáy, d: trung đoạn)

   b) Diện tích toàn phần của hình chóp

   Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và diện tích đáy:

   S_tp = S_xq + S    (S: diện tích đáy)

   2. Ví dụ: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, cạnh đáy là 8cm, chiều cao 10cm.

   + Tính diện tích xung quanh và diện tích toàn phần của hình chóp.

   + Tính thể tích của hình chóp.

   Hướng dẫn:

   

   Ta có ABCD là hình vuông, khi đó nửa chu vi bằng:

   

   + BD = AC = √ (8² + 8²) = 8√ 2 ( cm ) ⇒ AO = BO = CO = DO = 4√ 2 ( cm )

   Do đó:

   + Diện tích xung quanh của hình chóp đều là S_xq = p.d = p.OB = 16.4√ 2 = 64√ 2 ( cm² ).

   + Diện tích toàn phần của hình chóp đều là

   S_tp = S_xq + S_ABCD = 64√ 2 + 8² = 64 + 64√ 2 ( cm² )

   + Thể tích của hình chóp đều là V = 1/3S.h = 1/3.S_ABCD.SO = 1/3.8².10 = 640/3( cm³ )

2. Giáo án Diện tích xung quanh của hình chóp đều (2023) – Toán 8

   Mời các quý thầy cô cùng tham khảo và tải về chi tiết tài liệu dưới đây:

   Giáo án Toán 8 Bài 8: Diện tích xung quanh của hình chóp đều

   A. Mục tiêu

   1. Kiến thức: –  nắm vững cách tính diện tích xung quanh của hình chóp đều.

                          –  biết áp dụng cụng thức để tính với hình cụ thể.

                          – Liên hệ bài học với thực tiễn.

   2. Kỹ năng: – Rèn kỹ năng vẽ hình.

   3. Thái độ: –  tự giác, tích cực

   4. Phát triển năng lực: vẽ hình và tính toán

   B. Chuẩn bị

     1. Giáo viên: MÔ hình hình chóp đều.

     2. Học sinh  Thước thẳng com pa.

   C. Tiến trình bài dạy

   1. Tổ chức lớp: Kiểm diện

   2. Kiểm tra bài cũ:

   ? nêu khái niệm về hình chóp, hình chóp đều, hình chóp cụt đều

   3. Bài mới:

   Hoạt động của giáo viên

   Hoạt động của học sinh

   Ghi bảng

   Hoạt động 1: Khởi động
   – Thế nào là hình chóp, hình chóp đều. Cho biết đỉnh, cạnh bên, mặt bên, mặt đáy, đường cao, trung đọan của hình chóp đều ( GV treo hình chóp đều). – Cho HS nhận xét. GV cho điểm.	– HS lần lượt trả lời theo SGK.
   Hoạt động 2: Hình thành kiến thức
   – GV treo hình 123, yêu cầu HS trả lời ?. – Tổng diện tích tất cả các mặt bên của hình chóp là 48cm2 có phải là diện tích xung quanh của hình chóp đều không ? – GV giới thiệu công thức tính diện tích xung quanh. – GV giới thiệu công thức tính diện tích toàn phần.	– 4 HS lần lượt trả lời. – Tổng diện tích tất cả các mặt bên của hình chóp là 48cm2 là diện tích xung quanh của hình chóp đều. – HS nghe và ghi nhớ. – HS nghe và ghi nhớ.	1. Công thức tính diện tích xung quanh: ?. a/ Số các mặt bằng nhau trong một hình chóp tứ giác đều là 4. b/ Diện tích mỗi mặt tam giác là 12cm2. c/ Diện tích đáy của hình chóp đều là 16cm2. d/ Tổng diện tích tất cả các mặt bên của hình chóp là 48cm2. *  Diện tích xung quanh của hình chóp đều bằng tích nửa chu vi đáy với trung đoạn: S = p.d ( p là nửa chu vi đáy, d là trung đoạn của hình chóp đều). * Diện tích toàn phần của hình chóp đều bằng tổng diện tích xung quanh và diện tích đáy.
   – Yêu cầu HS đọc và tìm hiểu lời giải. – Để tính diện tích xung quang của hình bên người ta làm gì ? – Muốn tìm trung đoạn người ta vận dụng kiến thức nào ?	– Cả lớp thực hiện. – Tính nửa chu vi đáy và trung đoạn. – Vận dụng định lý Py-ta-go vào tam giác vuông SIC.	2. Ví dụ: SGK
   Hoạt động 3: Luyện tập
   BT 40-SGK. – Yêu cầu HS đọc đề bài, tìm lời giải. – 1 HS lên bảng. – Cho HS nhận xét.	BT 40-SGK. Ta có: + Nửa chu vi đáy: p = 30.2 = 60cm + Trung đoạn: d2 = 252 – 152 = 400 ⇒ d = 20cm. + Diện tích xung quanh của hình chóp đều là:  Sxq = 60.20 = 1200cm2. + Diện tích đáy của hình chóp là: Sđáy = 302 = 900cm2. + Diện tích toàn phần của hình chóp đều là: Stp = 1200 + 900 = 2100cm2.
   BT 43 – SGK. –   3HS lên bảng. – Cho HS nhận xét.	BT 43a – SGK. a/ Vì đây là hình chóp tứ giác đều nên đáy là hình vuông, ta có: + Sxq = 20.2.20 = 800cm2. + Stp = 800 + 202 = 800 + 400 = 1200cm2. b/ Vì đây là hình chóp tứ giác đều nên đáy là hình vuông, ta có: + Sxq = 7.2.12 = 168cm2. + Stp = 168 + 72 = 168 + 49 = 217cm2. c/ Vì đây là hình chóp tứ giác đều nên đáy là hình vuông, ta có: + Trung đoạn d = SI = + Sxq = 16.2.15 = 480cm2. + Stp = 480 + 162 = 736cm2
   4. VẬN DỤNG
   1. Viết công thức tính diện tích xung quanh của hình chóp. 2. Diện tích xung quanh của hình chóp không đều tính như thế nào. 3. Tìm cách tính diện tích xung quanh, diện tích toàn phần của hình chóp cụt đều.	* Làm bài tập phần vận dụng.
   5. MỞ RỘNG
   Vẽ sơ đồ tư duy khỏi quát nội dung bài học. Sưu tầm và làm một số bài tập nâng cao.	Làm bài tập phần mở rộng.

   4.Hướng dẫn học sinh tự học

               1. Học thuộc các khái niệm hình chóp, hình chóp tứ giác đều.

               2. Làm bài tập 42, 43 (SGK – Tr121).

               3. Tiết 65 “Bài 9.  Thể tích hình chóp đều”

3. Lý thuyết Diện tích xung quanh của hình lăng trụ đứng (mới 2023) – Toán 8

   Lý thuyết Diện tích xung quanh của hình lăng trụ đứng

   a) Công thức diện tích xung quanh

   Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao:

   S_xq = 2p.h    (p: nửa chu vi đáy, h: chiều cao)

   b) Diện tích toàn phần

   Diện tích toàn phần của hình lăng trụ đứng bằng tổng diện tích xung quanh và diện tích hai đáy.

   S_tp = S_xq + 2S    (S: điện tích đáy)

   Ví dụ: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều, AB = 4cm,AA’ = 5cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lặng trụ ABC.A’B’C’ ?

   

4. Giáo án Diện tích xung quanh của hình lăng trụ đứng (2023) – Toán 8

   Mời các quý thầy cô cùng tham khảo và tải về chi tiết tài liệu dưới đây:

   Giáo án Toán 8 Bài 5: Diện tích xung quanh của hình lăng trụ đứng

   A. Mục tiêu

   1. Kiến thức: – HS nêu lên được các công thức tính diện tích xung quanh, diện tích toàn phần của hình lăng trụ.

   – Biết cách vận dụng vào giải các bài toán thực tế.

   2. Kỹ năng: – Biết cách vận dụng vào giải các bài toán thực tế.

   3. Thái độ: tự giác, tích cực hợp tác.

   4. Phát triển năng lực: – Tính toán các bài toán hình học trong thực tế.

   B. Chuẩn bị

   1.Giáo viên: MÔ hình hình lăng trụ đứng. Bìa cắt khai triển, vẽ hình không gian.

   2. Học sinh:Làm đủ bài tập để phục vô bài mới

   C. Phương pháp: vấn đáp, nêu và giải quyết vấn đề,…

   D. Tiến trình bài dạy

   1. Tổ chức lớp: Kiểm diện

   2. Kiểm tra bài cũ:      GV đặt vấn đề vào bài

   3. Bài mới:

   Nội dung

   Hoạt động của giáo viên

   Hoạt động của học sinh

   1. KHỞI ĐỘNG
   GV nêu câu hỏi và thang điểm Gọi một HS lên bảng Gọi HS khác nhận xét Đánh giá cho điểm và chốt lại vấn đề.	Một HS lên bảng trả lời Cả lớp theo dõi, nhận xét. Đáp: Sai, trong lăng trụ xiên có thể có mặt bên là hình chữ nhật	–   Hình lăng trụ là hình như thế nào?  (4đ) –   Nêu sự khác nhau của lăng trụ đứng và lăng trụ xiên (cạnh bên và mặt đáy? Cạnh và đường cao?)?  (4đ) –   Câu nói sau đây đúng hay sai? Giải thích: “Trong hình lăng trụ xiên thì các mặt bên của nó không thể là hình chữ nhật”.  (2đ)
   Hoạt động 2. Hình thành kiến thức
   GV giới thiệu trực tiếp bài và ghi bảng Tìm diện tích xung quanh của lăng trụ? (Mỗi mặt của lăng trụ là hình gì? ⇒ Sxq?) Trường hợp lăng trụ đứng đáy là a1, a2, …, an cạnh bên là l thì sao? Muốn tìm diện tích toàn phần của lăng trụ ta làm sao? GV tóm tắt ghi bảng	HS ghi bài HS suy nghĩ HS: hình bình hành ⇒ Sxq= tổng dt các hbh Sxq= a1l + a2l + … + anl = (a1+ a2 +…+ an)l = pl HS: ta cộng Sxq với diện tích hai đáy HS ghi bài	1. Diện tích xung quanh:  –  Diện tích xung quanh của lăng trụ là tổng diện tích các mặt bên: Sxq = S1 + S2 + … + Sn  –  Trường hợp lăng trụ đứng thì: Sxq = pl (p là chu vi đáy, l là độ dài cạnh bên)  –  Diện tích toàn phần của lăng trụ bằng tổng của diện tích xung quanh với hai lần diện tích đáy. Stp = Sxq + 2Sđ
   Ơ lớp 5 đã tính thể tích hình hộp ⇒ thể tích lăng trụ cũng như hình hộp.	HS yếu tố lại công thức tính thể tích hình hộp.	2. Thể tích: V = B.h (B là diện tích đáy, h là độ dài đường cao)
   Gọi HS đọc ví dụ sgk GV ghi bảng – vẽ hình Nhìn hình yếu tố lại đề toán? Viết kết luận của đề? Em hãy thử tính? Gọi HS cho biết kết quả GV ghi bảng Gọi HS khác nhận xét GV hoàn chỉnh bài giải	HS đọc ví dụ (sgk) HS yếu tố lại đề bài toán Viết kết luận đề HS làm bài ít phút, sau đó đứng tại chỗ trả lời kết quả HS khác nhận xét HS ghi bài
   Hoạt động 3: Luyện tập
   GV yêu cầu Gọi HS đọc đề bài GV theo dõi GV tóm tắt ghi bảng	HS làm bài tập 2 sgk HS đọc đề bài Cả lớp cùng làm ít phút HS đứng tại chỗ trả lời
   Hoạt động 4: Vận dụng
   5. MỞ RỘNG
   Vẽ sơ đồ tư duy khỏi quát nội dung bài học Sưu tầm và làm một số bài tập nâng cao	Làm bài tập phần mở rộng.

   5. Hướng dẫn học sinh tự học(2P)

   – Học theo SGK.

   – Làm bài tập 24, 25,26 (SGK- 111, 112)

   HD:Bài 26: Để xem có gấp được  hay không dựa trên những yếu tố nào? Đỉnh nào trùng nhau, cạnh nào trùng nhau sau khi gấp.

5. Sách bài tập Toán 7 Bài 4 (Chân trời sáng tạo): Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

   Giải SBT Toán lớp 7 Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

   Giải trang 63 Tập 1

   Bài 1 trang 63 Sách bài tập Toán 7 Tập 1: Một chiếc hộp hình hộp chữ nhật có đáy là hình vuông cạnh 3 cm, chiều cao 7 cm. Nam cắt chiếc hộp thành hai hình lăng trụ đứng tứ giác với kích thước các đoạn cắt trên như Hình 6.

   

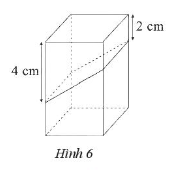
   Tính thể tích của hai hình lăng trụ đứng tứ giác sau khi cắt.

   Lời giải

   Quan sát Hình 6 ta thấy hai hình lăng trụ vừa cắt là hai hình lăng trụ đứng tứ giác có đáy là hình thang.

   Hình lăng trụ đứng phía trên có chiều cao h₁ = 3 cm và đáy là hình thang có các kích thước là 4 cm (đáy lớn), 2 cm (đáy bé), 3 cm (chiều cao hình thang).

   Diện tích đáy của hình lăng trụ đứng ở phía trên là: S₁ = (4 + 2) . 3 : 2 = 9 (cm²).

   Thể tích của hình lăng trụ đứng ở phía trên là: V₁ = S₁ . h₁ = 9 . 3 = 27 (cm³).

   Thể tích của hình hộp chữ nhật là: V = 3 . 3 . 7 = 63 (cm³).

   Thể tích của hình lăng trụ đứng ở phía dưới là: V₂ = V – V₁ = 63 – 27 = 36 (cm³).

   Bài 2 trang 63 Sách bài tập Toán 7 Tập 1: Mô hình một ngôi nhà có kích thước như Hình 7. Tính thể tích của mô hình ngôi nhà.

   

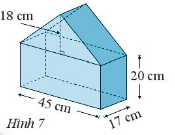
   Lời giải

   Cách 1:

   Quan sát Hình 7 ta thấy mô hình ngôi nhà gồm hai hình lăng trụ đứng (lăng trụ đứng tam giác và lăng trụ đứng tứ giác) ghép với nhau cùng có chiều cao là h = 17 cm.

   + Hình lăng trụ đứng tứ giác có đáy là hình chữ nhật với các kích thước là 45 cm và 20 cm nên diện tích đáy này là: S₁ = 45 . 20 = 900 (cm²).

   Thể tích hình lăng trụ đứng tứ giác là: V₁ = S₁ . h = 900 . 17 = 15 300 (cm³).

   + Hình lăng trụ đứng tam giác có đáy là tam giác có chiều cao là 18 cm và cạnh đáy ứng với chiều cao đó có độ dài là 45 cm nên diện tích đáy này là: S₂ = $\frac{1}{2}$ . 18 . 45 = 405 (cm²).

   Thể tích hình lăng trụ đứng tam giác là: V₂ = S₂ . h = 405 . 17 = 6 885 (cm³).

   Vậy thể tích của mô hình ngôi nhà là: V = V₁ + V₂ = 15 300 + 6 885 = 22 185 (cm³).

   Cách 2:

   Có thể xem mô hình ngôi nhà là hình lăng trụ có đáy là hình gồm một tứ giác và tam giác ghép lại và chiều cao h = 17 cm.

   Diện tích mặt đáy là: S = 45 . 20 + $\frac{1}{2}$ . 18 . 45 = 1 305 (cm²).

   Thể tích của mô hình ngôi nhà là: V = S . h = 1 305 . 17 = 22 185 (cm³).

   Bài 3 trang 63 Sách bài tập Toán 7 Tập 1: Một khối gỗ có kích thước như Hình 8 (đơn vị dm).

   

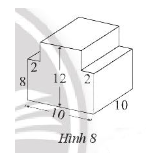
   a) Tính thể tích của khối gỗ.

   b) Tính diện tích toàn phần của khối gỗ.

   Lời giải

   a) Quan sát Hình 8 ta thấy khối gỗ được ghép bởi hai khối hộp chữ nhật.

   + Khối hộp chữ nhật ở phía dưới có kích thước là 10 dm, 8 dm và 10 dm, do đó thể tích của khối hộp chữ nhật phía dưới là: V₁ = 10 . 8 . 10 = 800 (dm³).

   + Khối hộp chữ nhật ở phía trên có:

   – Chiều dài là 10 dm;

   – Chiều rộng là: 10 – 2 – 2 = 6 (dm);

   – Chiều cao là: 12 – 8 = 4 (dm).

   Thể tích của khối hộp chữ nhật ở phía trên là: V₂ = 10 . 6 . 4 = 240 (dm³).

   Vậy thể tích của khối gỗ là V = V₁ + V₂ = 800 + 240 = 1 040 (dm³).

   b) Có thể xem khối gỗ là hình lăng trụ có đáy hình gồm 2 hình chữ nhật ghép lại với nhau và chiều cao là h = 10 dm.

   Chu vi đáy là: CV_đáy = 10 + 8 + 2 + 4 + 6 + 4 + 2 + 8 = 44 (dm).

   Diện tích xung quanh của khối gỗ là: S_xq = CV_đáy  . h = 44 . 10 = 440 (dm²).

   Diện tích hai mặt đáy là: S_2đáy = 2 . (10 . 8 + 6 . 4) = 208 (dm²).

   Diện tích toàn phần của khối gỗ là: S_tp = S_xq + S_2đáy = 440 + 208 = 648 (dm²).

   Bài 4 trang 63 Sách bài tập Toán 7 Tập 1: Một chi tiết máy bằng thép hình lăng trụ đứng tứ giác có đáy là một hình thoi có độ dài hai đường chéo là 16 cm và 18 cm, chiều cao 10 cm. Người ta khoét một lỗ hình hộp chữ nhật (Hình 9) có kích thước hai cạnh đáy là 2 cm và 6 cm. Tính thể tích còn lại của khối thép.

   

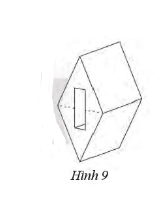
   Lời giải

   Diện tích đáy hình thoi của khối lăng trụ là: S_đ = $\frac{1}{2}$ . 16 . 18 = 144 (cm²).

   Thể tích của hình lăng trụ có đáy là hình thoi là: V = 144 . 10 = 1 440 (cm³).

   Lỗ hình hộp chữ nhật có kích thước hai cạnh đáy là 2 cm và 6 cm và chiều cao chính bằng chiều cao của hình lăng trụ có đáy là hình thoi và là 10 cm. Do đó, thể tích cái lỗ hình hộp chữ nhật là: V_l = 2 . 6 . 10 = 120 (cm³).

   Thể tích còn lại của khối thép là: V_cl = V – V_l = 1 440 – 120 = 1 320 (cm³).

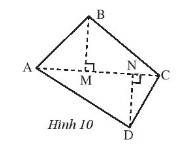
   Bài 5 trang 63 Sách bài tập Toán 7 Tập 1: Tính thể tích của một hình lăng trụ đứng đáy là một tứ giác như Hình 10, có độ dài AC = 5 m, BM = DN = 3 m, chiều cao của lăng trụ 7 m.

   

   Lời giải

   Từ Hình 10, ta thấy đáy của hình lăng trụ là một tứ giác, ta chia tứ giác đó thành 2 tam giác.

   Tam giác ABC có chiều cao BM = 3 m và cạnh đáy AC = 5 m, diện tích tam giác ABC là S_ABC = $\frac{1}{2}$BM . AC = $\frac{1}{2}$ . 3 . 5 = $\frac{15}{2}$ (m²).

   Tam giác ADC có chiều cao DN = 3 m và cạnh đáy AC = 5 m, diện tích tam giác ADC là S_ADC = $\frac{1}{2}$DN . AC = $\frac{1}{2}$ . 3 . 5 = $\frac{15}{2}$ (m²).

   Diện tích đáy của hình lăng trụ đã cho là: S_đ = S_ABC + S_ADC = $\frac{15}{2}$ + $\frac{15}{2}$ = 15 (m²).

   Thể tích của hình lăng trụ là: V = S_đ . h = 15 . 7 = 105 (m³).

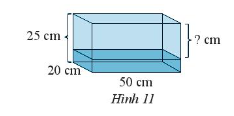
   Bài 6 trang 63 Sách bài tập Toán 7 Tập 1: Một bể cá có kích thước như Hình 11, người ta đổ vào đó 6,25 lít nước. Khoảng cách từ mực nước đến miệng bể là bao nhiêu?

   

   Lời giải

   Bể cá có dạng hình hộp chữ nhật có các kích thước là 20 cm, 50 cm, 25 cm.

   Thể tích của bể cá là: 20 . 50 . 25 = 25 000 (cm³).

   Đổi: 6,25 lít = 6,25 dm³ = 6 250 cm³.

   Thể tích phần bể không chứa nước là: 25 000 – 6 250 = 18 750 (cm³).

   Phần bể không chứa nước có dạng hình hộp chữ nhật có kích thước đáy giống bể cá và chiều cao chính là khoảng cách từ mực nước đến miệng bể.

   Vậy khoảng cách từ mực nước đến miệng bể là:  (cm).

   Giải trang 64 Tập 1

   Bài 7 trang 64 Sách bài tập Toán 7 Tập 1: Một khối bê tông hình lăng trụ đứng tam giác, bên trong khoét một cái lỗ có kích thước như Hình 12 (đơn vị dm).

   

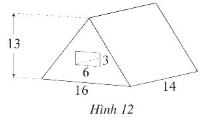
   Tính thể tích của khối bê tông.

   Lời giải

   Thể tích của hình lăng trụ đứng tam giác là: V₁ = $\left(\frac{1}{2}\mathrm{.13.16}\right).14=1456$ (dm³).

   Phần lỗ khoét có dạng hình hộp chữ nhật với các kích thước là 3 dm, 6 dm và 14 dm nên thể tích cái lỗ là: V₂ = 3 . 6 . 14 = 252 (dm³).

   Thể tích của khối bê tông là: V = V₁ – V₂ = 1 456 – 252 = 1 204 (dm³).

   Bài 8 trang 64 Sách bài tập Toán 7 Tập 1: Một công trường xây dựng cần 30 khúc gỗ để làm khung cho một tòa nhà. Mỗi khúc gỗ có dạng hình hộp chữ nhật đáy là hình vuông cạnh 0,5 m, chiều dài 8 m. Hỏi phần không gian mà 30 khúc gỗ chiếm là bao nhiêu?

   

   Lời giải

   Thể tích của một khúc gỗ dạng hình hộp chữ nhật là: V₁ = 0,5 . 0,5 . 8 = 2 (m³).

   30 khúc gỗ có thể tích là: 2 . 30 = 60 (m³).

   Vậy phần không gian mà 30 khúc gỗ chiếm có thể tích là 60 m³.

   Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

   Bài 3: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

   Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

   Bài tập cuối chương 3

   Bài 1: Các góc ở vị trí đặc biệt

   Bài 2: Tia phân giác