20 câu Trắc nghiệm Hệ bất phương trình bậc nhất hai ẩn (Chân trời sáng tạo 2023) có đáp án – Toán lớp 10

Trắc nghiệm Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn

I. Nhận biết

Câu 1. Điểm O(0; 0) thuộc miền nghiệm của hệ bất phương trình nào sau đây?

A. $\left\{\begin{array}{l}x+3y-6<0\\ 2x+y+4<0\end{array}\right.;$

B.  $\left\{\begin{array}{l}x+3y-6>0\\ 2x+y+4>0\end{array}\right.;$

C. $\left\{\begin{array}{l}x+3y-6>0\\ 2x+y+4<0\end{array}\right.;$

D. $\left\{\begin{array}{l}x+3y-6<0\\ 2x+y+4>0\end{array}\right..$

Hướng dẫn giải

Đáp án: D

Giải thích:

Ta có: $\left\{\begin{array}{l}0+3.0-6=-6<0\\ 2.0+0+4=4>0\end{array}\right.$ nên cặp số O(0; 0) thỏa mãn đồng thời cả hai bất phương trình của hệ $\left\{\begin{array}{l}x+3y-6<0\\ 2x+y+4>0\end{array}\right..$

Do đó điểm O(0; 0) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x+3y-6<0\\ 2x+y+4>0\end{array}\right..$

Vậy ta chọn phương án D.

Câu 2. Cho hệ bất phương trình $\left\{\begin{array}{l}x>0\\ 2x-\frac{3}{2}y-1\ge 0\\ 4x-3y-2\le 0\end{array}\right..$ Khẳng định nào sau đây là sai?

A. Biểu diễn miền nghiệm của hệ bất phương trình là miền không kể bờ x = 0;

B. Biểu diễn miền nghiệm của hệ bất phương trình là miền kể bờ $2x-\frac{3}{2}y-1=0;$

C. Biểu diễn miền nghiệm của hệ bất phương trình là miền kể cả bờ 4x – 3y – 2 = 0;

D. Miền nghiệm của hệ bất phương trình là miền chứa gốc toạ độ.

Hướng dẫn giải

Đáp án: D

Giải thích:

Xét hệ bất phương trình $\left\{\begin{array}{l}x>0\\ 2x-\frac{3}{2}y-1\ge 0\\ 4x-3y-2\le 0\end{array}\right..$

+ Khi đó biểu diễn miền nghiệm của hệ bất phương trình là miền:

• Không kể bờ x = 0;

• Có kể bờ 2x – .$.\frac{3}{2}.$.y – 1 = 0;

• Có kể bờ 4x – 3y – 2 = 0.

+ Xét điểm O(0; 0) ta có hoành độ của điểm O không thỏa mãn x > 0 nên miền nghiệm của hệ bất phương trình là miền không chứa gốc toạ độ.

Vậy ta chọn phương án D.

Câu 3. Hệ bất phương trình nào dưới đây là hệ bất phương trình bậc nhất hai ẩn:

A.  $\left\{\begin{array}{l}x+y-1<0\\ 2x+y>0;\end{array}\right.$

B. $\left\{\begin{array}{l}x-y=0\\ 2x+y-4=0;\end{array}\right.$

C. $\left\{\begin{array}{l}x\ge 0\\ 3x^2+2y-1<0;\end{array}\right.$ 

D. $\left\{\begin{array}{l}x+y\le 1\\ x+2y^3-1>0.\end{array}\right.$  

Hướng dẫn giải

Đáp án: A

Giải thích:

• Xét phương án A: $\left\{\begin{array}{l}x+y-1<0\\ 2x+y>0\end{array}\right.$

Hệ bất phương trình trên có hai bất phương trình x + y – 1 < 0 và 2x + y > 0 đều là bất phương trình bậc nhất hai ẩn.

• Xét phương án B: $\left\{\begin{array}{l}x-y=0\\ 2x+y-4=0\end{array}\right.$

Hệ trên là hệ phương trình bậc nhất hai ẩn không phải là hệ bất phương trình bậc nhất hai ẩn.

• Xét phương án C: $\left\{\begin{array}{l}x\ge 0\\ 3x^2+2y-1<0\end{array}\right.$

Hệ bất phương trình trên có bất phương trình 3x² + 2y – 1 < 0 chứa x² nên không phải là hệ bất phương trình bậc nhất hai ẩn.

• Xét phương án D: $\left\{\begin{array}{l}x+y\le 1\\ x+2y^3-1>0\end{array}\right.$

Hệ bất phương trình trên có bất phương trình x + 2y³ – 1 > 0 chứa y³ nên không phải là hệ bất phương trình bậc nhất hai ẩn.

Vậy ta chọn phương án A.

Câu 4. Hệ bất phương trình $\left\{\begin{array}{l}x>0\\ x+\sqrt{3}y+1>0\end{array}\right.$ có miền nghiệm không chứa điểm nào sau đây?

A. A(–1; 2);

B. B$\left(\sqrt{2};0\right);$

C. C$\left(1;\sqrt{3}\right);$

D. D$\left(\sqrt{3};0\right).$

Hướng dẫn giải

Đáp án: A

Giải thích:

Hệ bất phương trình $\left\{\begin{array}{l}x>0\\ x+\sqrt{3}y+1>0\end{array}\right.$ có bất phương trình x > 0.

Mà điểm A(–1; 2) có x = –1 < 0 nên miền nghiệm của hệ bất phương trình không chứa điểm A(–1; 2).

Vậy ta chọn phương án A.

Câu 5. Cho hệ bất phương trình $\left\{\begin{array}{l}x-y>0\\ x-3y+3<0\\ x+y-5>0\end{array}\right..$ Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho:

A. A(–2; 2);

B. B(5; 3);

C. C(1; –1);

D. O(0; 0).

Hướng dẫn giải

Đáp án: B

Giải thích:

Cách 1: Xét từng phương án.

• Xét điểm A(–2; 2):

Ta có: $\left\{\begin{array}{l}-2-2=-4<0\\ -2-3.2+3=-5<0\\ -2+2-5=-5<0\end{array}\right.$

Do đó cặp số (–2; 2) không thỏa mãn đồng thời ba bất phương trình của hệ đã cho.

Vậy điểm A(–2; 2) không thuộc miền nghiệm của hệ bất phương trình đã cho.

• Xét điểm B(5; 3):

Ta có: $\left\{\begin{array}{l}5-3=2>0\\ 5-3.3+3=-1<0\\ 5+3-5=3>0\end{array}\right.$

Do đó cặp số (5; 3) thỏa mãn đồng thời ba bất phương trình của hệ đã cho.

Vậy điểm B(5; 3) thuộc miền nghiệm của hệ bất phương trình đã cho.

Đến đây ta có thể chọn phương án B.

• Xét điểm C(1; –1):

Ta có: $\left\{\begin{array}{l}1-\left(-1\right)=2>0\\ 1-3.\left(-1\right)+3=7>0\\ 1+\left(-1\right)-5=-5<0\end{array}\right.$

Do đó cặp số (1; –1) không thỏa mãn đồng thời ba bất phương trình của hệ đã cho.

Vậy điểm C(1; –1) không thuộc miền nghiệm của hệ bất phương trình đã cho.

• Xét điểm O(0; 0):

Ta có: $\left\{\begin{array}{l}0-0=0\\ 0-3.0+3=3>0\\ 0+0-5=-5<0\end{array}\right.$

Do đó cặp số (0; 0) không thỏa mãn đồng thời ba bất phương trình của hệ đã cho.

Vậy điểm O(0; 0) không thuộc miền nghiệm của hệ bất phương trình đã cho.

Ta chọn phương án B.

Cách 2:

• Ta thấy hệ có bất phương trình x – y > 0 nên ta có x > y.

Do đó điểm thuộc miền nghiệm của hệ phải thỏa mãn hoành độ lớn hơn tung độ.

Khi đó ta loại phương án A và D.

• Hệ có bất phương trình x + y – 5 > 0 nên x + y > 5.

Do đó điểm thuộc miền nghiệm của hệ phải thỏa mãn tổng hoành độ và tung độ lớn hơn 5. Ta loại phương án C.

Vậy ta chọn phương án B.

Câu 6. Trong các cặp số (x; y) sau, cặp số không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x+y-2\le 0\\ 2x-3y+2>0\end{array}\right.$ là:

A. (–1; –1);

B. (1; 1);

C. (–1; 1);

D. (0; 0).

Hướng dẫn giải

Đáp án: C

Giải thích:

• Xét điểm (–1; –1):

Ta có: $\left\{\begin{array}{l}-1+\left(-1\right)-2=-4\le 0\\ 2.\left(-1\right)-3.\left(-1\right)+2=3>0\end{array}\right.$

Do đó cặp số (–1; –1) thỏa mãn đồng thời cả hai bất phương trình của hệ đã cho.

Vậy cặp số (–1; –1) là nghiệm của hệ bất phương trình đã cho.

• Xét điểm (1; 1):

Ta có: $\left\{\begin{array}{l}1+1-2=0\le 0\\ 2.1-3.1+2=1>0\end{array}\right.$

Do đó cặp số (1; 1) thỏa mãn đồng thời cả hai bất phương trình của hệ đã cho.

Vậy cặp số (1; 1) là nghiệm của hệ bất phương trình đã cho.

• Xét điểm (–1; 1):

Ta có: $\left\{\begin{array}{l}-1+1-2=-2\le 0\\ 2.\left(-1\right)-3.1+2=-3<0\end{array}\right.$

Do đó cặp số (–1; 1) không thỏa mãn đồng thời cả hai bất phương trình của hệ đã cho.

Vậy cặp số (–1; 1) là không nghiệm của hệ bất phương trình đã cho.

• Xét điểm (0; 0):

Ta có: $\left\{\begin{array}{l}0+0-2=-2\le 0\\ 2.0-3.0+2=2>0\end{array}\right.$

Do đó cặp số (0; 0) thỏa mãn đồng thời cả hai bất phương trình của hệ đã cho.

Vậy cặp số (0; 0) là nghiệm của hệ bất phương trình đã cho.

Ta chọn phương án C.

Câu 7. Miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x+y-2\ge 0\\ x+2y+1\le 0\end{array}\right.$là miền chứa điểm nào sau đây?

A. M(0; 1);

B. N(8; –5);

C. P(1; 2);

D. Q(–2; 0).

Hướng dẫn giải

Đáp án: B

Giải thích:

• Xét điểm M(0; 1):

Ta có: $\left\{\begin{array}{l}0+1-2=-1<0\\ 0+2.1+1=3>0\end{array}\right.$

Do đó cặp số (0; 1) không thỏa mãn đồng thời cả hai bất phương trình của hệ đã cho.

Vậy miền nghiệm của hệ bất phương trình không chứa điểm M(0; 1).

• Xét điểm N(8; –5):

Ta có: $\left\{\begin{array}{l}8+\left(-5\right)-2=1\ge 0\\ 8+2.\left(-5\right)+1=-1\le 0\end{array}\right.$

Do đó cặp số (8; –5) thỏa mãn đồng thời cả hai bất phương trình của hệ đã cho.

Vậy miền nghiệm của hệ bất phương trình chứa điểm N(8; –5).

• Xét điểm P(1; 2):

Ta có: $\left\{\begin{array}{l}1+2-2=1\ge 0\\ 1+2.2+1=6>0\end{array}\right.$

Do đó cặp số (1; 2) không thỏa mãn đồng thời cả hai bất phương trình của hệ đã cho.

Vậy miền nghiệm của hệ bất phương trình không chứa điểm P(1; 2).

• Xét điểm Q(–2; 0):

Ta có: $\left\{\begin{array}{l}-2+0-2=-4<0\\ -2+2.0+1=-1\le 0\end{array}\right.$

Do đó cặp số (–2; 0) không thỏa mãn đồng thời cả hai bất phương trình của hệ đã cho.

Vậy miền nghiệm của hệ bất phương trình không chứa điểm Q(–2; 0).

Ta chọn phương án B.

II. Thông hiểu

Câu 1. Cho hệ bất phương trình $\left\{\begin{array}{l}3x+2y<1\left(1\right)\\ x+\frac{2}{3}y<1\left(2\right)\end{array}\right..$  Gọi S₁ là miền nghiệm của bất phương trình (1), S₂ là miền nghiệm của bất phương trình (2).

Cho các phát biểu sau:

(I) Miền nghiệm của hệ bất phương trình là S₁;

(II) Miền nghiệm của hệ bất phương trình là S₂;

(III) Hai bất phương trình của hệ có cùng miền nghiệm.

Số phát biểu đúng là:

A. 0;

B. 1;

C. 2;

D. 3.

Hướng dẫn giải

Đáp án: B

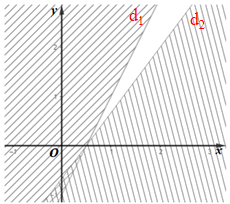
Giải thích: Ta có $\left\{\begin{array}{l}3x+2y<1\left(1\right)\\ x+\frac{2}{3}y<1\left(2\right)\end{array}\right.\iff \left\{\begin{array}{l}3x+2y-1<0\\ 3x+2y-3<0\end{array}\right.$

Biểu diễn miền nghiệm của hệ $\left\{\begin{array}{l}3x+2y-1<0\\ 3x+2y-3<0\end{array}\right.$ trên mặt phẳng Oxy.

• Miền nghiệm của bất phương trình 3x + 2y – 1 < 0 là nửa mặt phẳng (kể cả bờ d1: 3x + 2y – 1 = 0) chứa điểm O(0; 0).

• Miền nghiệm của bất phương trình 3x + 2y – 3 < 0 là nửa mặt phẳng (kể cả bờ d2: 3x + 2y – 3 = 0) chứa điểm O(0; 0).

Miền không gạch chéo (kể cả bờ d1, d2) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

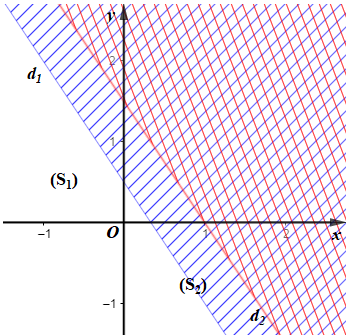
Do đó miền nghiệm của hệ bất phương trình là miền (S1) nên chỉ có (I) đúng.

Vậy ta chọn phương án B.

Câu 2. Cho hệ bất phương trình $\left\{\begin{array}{l}x-2y<0\\ m{x}^2+3y>0\\ 2x-\left(m^2-m\right)y^2\le 0\end{array}\right.$ (với m là tham số). Giá trị m để hệ bất phương trình đó là hệ bất phương trình bậc nhất hai ẩn x và y là:

A. m = 0;

B. m = 1;

C. m ∈ {0; 1};

D. m ∈ ∅.

Hướng dẫn giải

Đáp án: A

Giải thích:

Để hệ bất phương trình $\left\{\begin{array}{l}x-2y<0\\ m{x}^2+3y>0\\ 2x-\left(m^2-m\right)y^2\le 0\end{array}\right.$ là hệ bất phương trình bậc nhất hai ẩn x và y thì hệ số của x² và y² bằng 0.

Tức là $\left\{\begin{array}{l}m=0\\ m^2-m=0\end{array}\right.\iff \left\{\begin{array}{l}m=0\\ \left[\begin{array}{l}m=0\\ m=1\end{array}\right.\end{array}\right.\iff m=0.$

Vậy ta chọn phương án A.

Câu 3. Cho hệ bất phương trình $\left\{\begin{array}{l}x-2y<0\\ x+3y>-2\end{array}\right.$ và các điểm A(–1; 0), B(1; 0), C(–3; 4) và D(0; 3). Miền nghiệm của hệ bất phương trình chứa bao nhiêu điểm trong bốn điểm trên?

A. 1;

B. 2;

C. 3;

D. 4.

Hướng dẫn giải

Đáp án: C

Giải thích:

• Xét điểm A(–1; 0) ta có: $\left\{\begin{array}{l}-1-2.0=-1<0\\ -1+3.0=-1>-2\end{array}\right.$ thỏa mãn đồng thời cả hai bất phương trình nên miền nghiệm của hệ bất phương trình chứa điểm A(–1; 0).

• Xét điểm B(1; 0) ta có: $\left\{\begin{array}{l}1-2.0=1>0\\ 1+3.0=1>-2\end{array}\right.$ không thỏa mãn đồng thời cả hai bất phương trình nên miền nghiệm của hệ bất phương trình không chứa điểm B(1; 0).

• Xét điểm C(–3; 4) ta có: $\left\{\begin{array}{l}-3-2.4=-11<0\\ -3+3.4=9>-2\end{array}\right.$ thỏa mãn đồng thời cả hai bất phương trình nên miền nghiệm của hệ bất phương trình chứa điểm C(–3; 4).

• Xét điểm D(0; 3) ta có: $\left\{\begin{array}{l}0-2.3=-6<0\\ 0+3.3=9>-2\end{array}\right.$ thỏa mãn đồng thời cả hai bất phương trình nên miền nghiệm của hệ bất phương trình không chứa điểm D(0; 3).

Vậy miền nghiệm của hệ bất phương trình chứa ba điểm A, C, D trong 4 điểm.

Ta chọn phương án C.

Câu 4. Cho hệ bất phương trình $\left\{\begin{array}{l}2x-y-1\ge 0\\ 4x-3y-2\le 0\end{array}\right.$ . Miền nghiệm (miền không gạch chéo) của hệ bất phương trình được biểu diễn như trong hình vẽ nào sau đây?

A.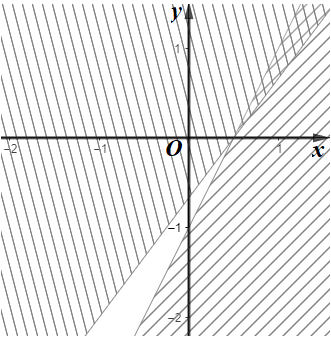 

B.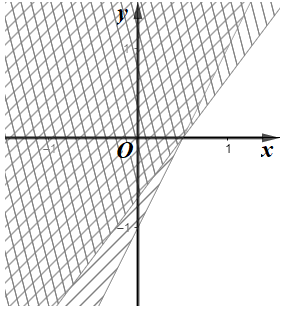 

C.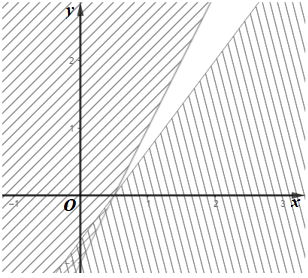 

D.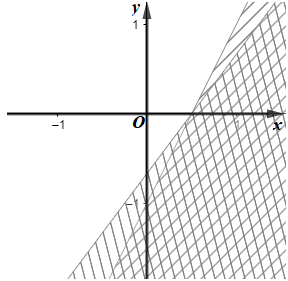 

Hướng dẫn giải

Đáp án: C

Giải thích:

Trên mặt phẳng Oxy:

• Biểu diễn miền nghiệm của bất phương trình: 2x – y – 1 ≥ 0.

Vẽ đường thẳng d₁: 2x – y – 1 = 0 đi qua hai điểm (0; –1) và (1; 1).

Xét điểm O(0; 0) ∉ d₁, ta có: 2.0 – 0 – 1 = –1 < 0 nên miền nghiệm của bất phương trình 2x – y – 1 ≥ 0 là nửa mặt phẳng (kể cả bờ d₁) không chứa điểm O(0; 0).

• Biểu diễn miền nghiệm của bất phương trình: 4x – 3y – 2 ≤ 0.

Vẽ đường thẳng d₂: 4x – 3y – 2 = 0 đi qua hai điểm (2; 2) và (–1; –2).

Xét điểm O(0; 0) ∉ d₂, ta có: 4.0 – 3.0 – 2 = –2 < 0 nên miền nghiệm của bất phương trình 4x – 3y – 2 ≤ 0 là nửa mặt phẳng (kể cả bờ d₂) chứa điểm O(0; 0).

Miền không gạch chéo (kể cả bờ d₁ và d₂) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

Vậy ta chọn phương án C.

Câu 5. Cho hệ bất phương trình: $\left\{\begin{array}{l}x+y-2\ge 0\\ x-3y+3<0\end{array}\right..$ Chọn khẳng định đúng:

A. Cặp số (1; 2) không phải là nghiệm của hệ phương trình;

B.  Miền nghiệm của hệ bất phương trình là miền kể cả bờ là đường thẳng x – 3y + 3 = 0;

C. Miền nghiệm của hệ bất phương trình chứa điểm $\left(\frac{3}{4};\frac{5}{4}\right);$

D. Miền nghiệm của hệ bất phương trình chứa tất cả các điểm nằm trên đường thẳng x + y – 2 = 0.

Hướng dẫn giải

Đáp án: D

Giải thích:

• Xét cặp số (1; 2):

Ta có: $\left\{\begin{array}{l}1+2-2=1\ge 0\\ 1-3.2+3=-2<0\end{array}\right.$ nên cặp số (1; 2) thỏa mãn đồng thời cả hai bất phương trình của hệ.

Do đó cặp số (1; 2) là nghiệm của hệ bất phương trình. Khi đó A sai.

• Xét cặp số $\left(\frac{3}{4};\frac{5}{4}\right)$:

$\left\{\begin{array}{l}\frac{3}{4}+\frac{5}{4}-2=0\ge 0\\ \frac{3}{4}-3.\frac{5}{4}+3=0\end{array}\right.$ nên cặp số $\left(\frac{3}{4};\frac{5}{4}\right)$ không thỏa mãn đồng thời cả hai bất phương trình của hệ.

Do đó cặp số $\left(\frac{3}{4};\frac{5}{4}\right)$ không là nghiệm của hệ bất phương trình nên miền nghiệm của hệ không chứa điểm $\left(\frac{3}{4};\frac{5}{4}\right)$. Khi đó C sai.

• Miền nghiệm của hệ bất phương trình là miền không kể bờ là đường thẳng x – 3y + 3 = 0. Do đó B sai.

• Miền nghiệm của hệ bất phương trình là miền kể cả bờ là đường thẳng x + y – 2 = 0. Do đó miền nghiệm của hệ chứa tất cả các điểm nằm trên đường thẳng x + y – 2 = 0.

Khi đó D đúng.

Vậy ta chọn phương án D.

Câu 6. Cho hệ bất phương trình: $\left\{\begin{array}{c}0\le y\le 4\\ x\ge 0\\ x-y-1\le 0\\ x+2y-10\le 0\end{array}\right..$ Miền nghiệm của hệ bất phương trình là:

A. Miền tứ giác;

B. Miền tam giác;

C. Miền ngũ giác;

D. Miền lục giác.

Hướng dẫn giải

Đáp án: C

Giải thích:

Ta có: $\left\{\begin{array}{c}0\le y\le 4\\ x\ge 0\\ x-y-1\le 0\\ x+2y-10\le 0\end{array}\right.\iff \left\{\begin{array}{c}\begin{array}{l}y\ge 0\\ y\le 4\end{array}\\ x\ge 0\\ x-y-1\le 0\\ x+2y-10\le 0\end{array}\right.$

Trên mặt phẳng Oxy:

• Biểu diễn miền nghiệm của bất phương trình: y ≥ 0.

Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d₁: y = 0) chứa điểm (0; 1).

• Biểu diễn miền nghiệm của bất phương trình: y ≤ 4.

Miền nghiệm của bất phương trình y ≤ 4 là nửa mặt phẳng (kể cả đường thẳng d₂: y = 4) chứa điểm (0; 1).

• Biểu diễn miền nghiệm của bất phương trình: x ≥ 0.

Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d₃: x = 0) chứa điểm (1; 0).

• Biểu diễn miền nghiệm của bất phương trình: x – y – 1 ≤ 0.

Vẽ đường thẳng d₄: x – y – 1 = 0 đi qua hai điểm (0; –1) và (1; 0).

Xét điểm O(0; 0) ∉ d1, ta có: 0 – 0 – 1 = –1 < 0 nên miền nghiệm của bất phương trình x – y – 1 ≥ 0 là nửa mặt phẳng (kể cả bờ d₄) chứa điểm O(0; 0).

• Biểu diễn miền nghiệm của bất phương trình: x + 2y – 10 ≤ 0.

Vẽ đường thẳng d₅: x + 2y – 10 = 0 đi qua hai điểm (0; 5) và (10; 0).

Xét điểm O(0; 0) ∉ d₁, ta có: 0 + 2.0 – 10 = –10 < 0 nên miền nghiệm của bất phương trình x + 2y – 10 ≤ 0 là nửa mặt phẳng (kể cả bờ d₅) chứa điểm O(0; 0).

Miền không gạch chéo (kể cả bờ d₁, d₂, d₃, d₄ và d₅) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

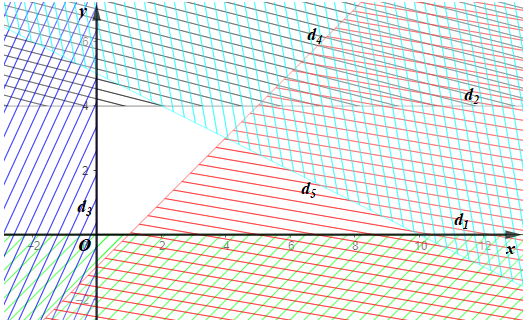
Vậy miền nghiệm của hệ bất phương trình là miền ngũ giác.

Ta chọn phương án C.

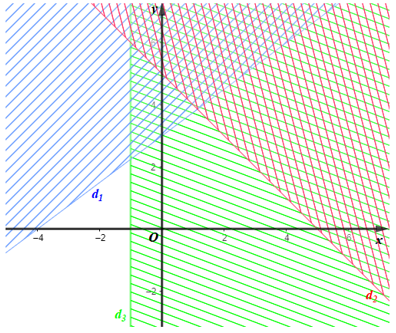
Câu 7. Cho các đường thẳng d₁: 3x – 4y + 12 = 0, d₂: x + y – 5 = 0 và d₃: x + 1 = 0.

Miền không gạch chéo (kể cả bờ d₁, d₂, d₃) trong hình vẽ bên dưới là miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình dưới đây?

A. $\left\{\begin{array}{l}3x-4y+12\le 0\\ x+y-5\le 0\\ x+1\le 0;\end{array}\right.$

B. $\left\{\begin{array}{l}3x-4y+12\ge 0\\ x+y-5\ge 0\\ x+1\ge 0;\end{array}\right.$

C. $\left\{\begin{array}{l}3x-4y+12\le 0\\ x+y-5\ge 0\\ x+1\le 0;\end{array}\right.$

D. $\left\{\begin{array}{l}3x-4y+12\ge 0\\ x+y-5\le 0\\ x+1\ge 0.\end{array}\right.$

Hướng dẫn giải

Đáp án: A

Giải thích:

Ta xét điểm O(0; 0):

$\left\{\begin{array}{l}3.0-4.0+12=12>0\\ 0+0-5=-5<0\\ 0+1=1>0.\end{array}\right.$

Do đó điểm O(0; 0) thuộc miền nghiệm của các bất phương trình:

$\left\{\begin{array}{l}3x-4y+12>0\\ x+y-5<0\\ x+1>0.\end{array}\right.$

Quan sát hình vẽ ta thấy miền nghiệm có:

• Nửa mặt phẳng bờ là đường thẳng d₁ (3x – 4y + 12 = 0) có chứa điểm O;

• Nửa mặt phẳng bờ là đường thẳng d₂ (x + y – 5 = 0) có chứa điểm O;

• Nửa mặt phẳng bờ là đường thẳng d₃ (x + 1 = 0) không chứa điểm O.

Do đó hệ bất phương trình cần tìm là $\left\{\begin{array}{l}3x-4y+12\ge 0\\ x+y-5\le 0\\ x+1\le 0.\end{array}\right.$

Vậy ta chọn phương án A

Câu 8. Cho hệ bất phương trình: $\left\{\begin{array}{l}2x+3y+6\ge 0\\ x\le 0\\ 2x-3y+1\ge 0\end{array}\right..$ Khẳng định nào sau đây là sai?

A. Miền nghiệm của hệ bất phương trình là miền tam giác ABC với A(0; –2), $B\left(0;\frac{1}{3}\right),$ $C\left(-\frac{7}{4};-\frac{5}{6}\right);$

B. Đường thằng y = –1 có hai giao điểm với miền nghiệm của hệ bất phương trình;

C. Miền nghiệm của hệ bất phương trình chứa gốc toạ độ;

B. Miền nghiệm của hệ bất phương trình là miền kể cả bờ 2x – 3y + 1 = 0.

Hướng dẫn giải

Đáp án: C

Giải thích:

• Xét điểm O(0; 0) ta có: $\left\{\begin{array}{l}2.0+3.0+6=6\ge 0\\ 0\le 0\\ 2.0-3.0+1=1\ge 0\end{array}\right.$

Nên cặp số (0; 0) thỏa mãn đồng thời cả ba bất phương trình của hệ.

Do đó miền nghiệm của hệ chứa gốc tọa độ O. Khi đó C là khẳng định đúng.

• Hệ bất phương trình $\left\{\begin{array}{l}2x+3y+6\ge 0\\ x\le 0\\ 2x-3y+1\ge 0\end{array}\right.$ có miền nghiệm kể cả bờ 2x – 3y + 1 = 0.

Do đó D là khẳng định đúng.

• Biểu diễn miền nghiệm của hệ bất phương trình:

Miền nghiệm của bất phương trình 2x + 3y + 6 ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d₁: 2x + 3y + 6 = 0) chứa điểm O(0; 0).

Miền nghiệm của bất phương trình x ≤ 0 là nửa mặt phẳng (kể cả đường thẳng d₂: x = 0) chứa điểm (–1; 0).

Miền nghiệm của bất phương trình 2x – 3y + 1 ≥ 0 là nửa mặt phẳng (kể cả đường thẳng _d3: 2x – 3y + 1 = 0) chứa điểm O(0; 0).

Miền không gạch chéo (kể cả bờ d₁, d₂, d₃) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

Miền nghiệm là miền tam giác ABC với A(0; –2), $B\left(0;\frac{1}{3}\right), C\left(-\frac{7}{4};-\frac{5}{6}\right).$  Khi đó A là khẳng định đúng.

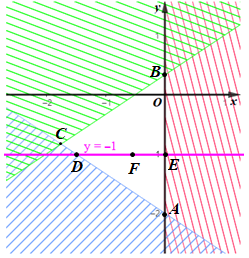
Vẽ đường thẳng y = –1 ta thấy đường thẳng y = –1 cắt cạnh AC tại D và cắt cạnh AB tại E và cắt miền trong tam giác ABC tại vô số điểm F. Do đó đường thẳng y = –1 cắt miền tam giác ABC tại vô số điểm.

Khi đó B là khẳng định sai.

Vậy ta chọn phương án B.

III. Vận dụng

Câu 1. Cho hệ bất phương trình $\left\{\begin{array}{l}x-y-1\le 0\\ x+4y+9\ge 0\\ x-2y+3\ge 0\end{array}\right..$ Biểu thức F(x; y) = 3x – 2y – 4 có giá trị nhỏ nhất bằng:

A. –20;

B. –17;

C. –3;

D. 3.

Hướng dẫn giải

Đáp án: B

Giải thích:

Biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng Oxy:

• Miền nghiệm của bất phương trình x – y – 1 ≤ 0 là nửa mặt phẳng (kể cả bờ d₁: x – y – 1 = 0) chứa điểm O(0; 0).

• Miền nghiệm của bất phương trình x + 4y + 9 ≥ 0 là nửa mặt phẳng (kể cả bờ d₂: x + 4y + 9 = 0) chứa điểm O(0; 0).

• Miền nghiệm của bất phương trình x – 2y + 3 ≥ 0 là nửa mặt phẳng (kể cả bờ d₁: x – y – 1 = 0) chứa điểm O(0; 0).

Miền không gạch chéo (kể cả bờ d₁, d₂) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

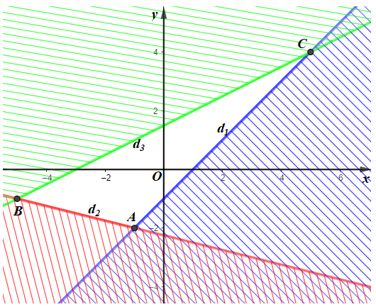
Miền nghiệm của hệ bất phương trình là miền tam giác ABC với A(–1; –2), B(–5; –1) và C(5; 4).

Xét biểu thức F(x; y) = 3x – 2y – 4.

Tại A(–1; –2): F = 3.(–1) – 2.(–2) – 4 = –3.

Tại B(–5; –1): F = 3.(–5) – 2.(–1) – 4 = –17.

Tại C(5; 4): F = 3.5 – 2.4 – 4 = 3.

F(x; y) đạt giá trị nhỏ nhất bằng –17 tại B(–5; –1).

Vậy ta chọn phương án B.

Câu 2. Cho hệ bất phương trình $\left\{\begin{array}{l}0\le y\le 4\\ x\ge 0\\ x-y-1\le 0\\ x+2y-10\le 0\end{array}\right..$ Gọi điểm có toạ độ (x; y) thuộc miền nghiệm của hệ bất phương trình sao cho F(x; y) = x + 2y đạt giá trị lớn nhất. Số điểm thoả mãn là:

A. 0;

B. 1;

C. 2;

D. 3.

Hướng dẫn giải

Đáp án: C

Giải thích:

Ta có: $\left\{\begin{array}{c}0\le y\le 4\\ x\ge 0\\ x-y-1\le 0\\ x+2y-10\le 0\end{array}\right.\iff \left\{\begin{array}{c}\begin{array}{l}y\ge 0\\ y\le 4\end{array}\\ x\ge 0\\ x-y-1\le 0\\ x+2y-10\le 0\end{array}\right.$

Trên mặt phẳng Oxy:

• Biểu diễn miền nghiệm của bất phương trình: y ≥ 0.

Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d₁: y = 0) chứa điểm (0; 1).

• Biểu diễn miền nghiệm của bất phương trình: y ≤ 4.

Miền nghiệm của bất phương trình y ≤ 4 là nửa mặt phẳng (kể cả đường thẳng d₂: y = 4) chứa điểm (0; 1).

• Biểu diễn miền nghiệm của bất phương trình: x ≥ 0.

Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d₃: x = 0) chứa điểm (1; 0).

• Biểu diễn miền nghiệm của bất phương trình: x – y – 1 ≤ 0.

Vẽ đường thẳng d₄: x – y – 1 = 0 đi qua hai điểm (0; –1) và (1; 0).

Xét điểm O(0; 0) ∉ d₁, ta có: 0 – 0 – 1 = –1 < 0 nên miền nghiệm của bất phương trình x – y – 1 ≥ 0 là nửa mặt phẳng (kể cả bờ d₄) chứa điểm O(0; 0).

• Biểu diễn miền nghiệm của bất phương trình: x + 2y – 10 ≤ 0.

Vẽ đường thẳng d₅: x + 2y – 10 = 0 đi qua hai điểm (0; 5) và (10; 0).

Xét điểm O(0; 0) ∉ d₁, ta có: 0 + 2.0 – 10 = –10 < 0 nên miền nghiệm của bất phương trình x + 2y – 10 ≤ 0 là nửa mặt phẳng (kể cả bờ d₅) chứa điểm O(0; 0).

Miền không gạch chéo (kể cả bờ d₁, d₂, d₃, d₄ và d₅) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

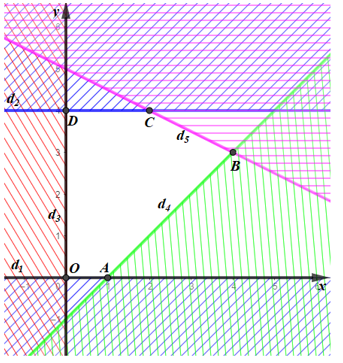
Miền nghiệm của hệ bất phương trình là miền ngũ giác OABCD với O(0; 0), A(1; 0), B(4; 3), C(2; 4) và D(0; 4).

Xét biểu thức F(x; y) = x + 2y:

Tại O(0; 0): F = 0 + 2.0 = 0;

Tại A(1; 0): F = 1 + 2.0 = 1;

Tại B(4; 3): F = 4 + 2.3 = 10;

Tại C(2; 4): F = 2 + 2.4 = 10;

Tại D(0; 4): F = 0 + 2.4 = 8.

F(x; y) đạt giá trị lớn nhất bằng 10 tại hai điểm B(4; 3) và C(2; 4).

Vậy có 2 điểm thỏa mãn yêu cầu đề bài. Ta chọn phương án C.

Câu 3. Cho hệ bất phương trình $\left\{\begin{array}{l}x\ge 0\\ x-y-1\le 0\\ x+2y-10\le 0\end{array}\right..$  Diện tích miền nghiệm của hệ bất phương trình bằng:

A. 6;

B. 12;

C. 24;

D. 28.

Hướng dẫn giải

Đáp án: B

Giải thích:

Trên mặt phẳng Oxy:

• Biểu diễn miền nghiệm của bất phương trình: x ≥ 0.

Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d₁: x = 0) chứa điểm (1; 0).

• Biểu diễn miền nghiệm của bất phương trình: x – y – 1 ≤ 0.

Vẽ đường thẳng d_2: x – y – 1 = 0 đi qua hai điểm (0; –1) và (1; 0).

Xét điểm O(0; 0) ∉ _d2, ta có: 0 – 0 – 1 = –1 < 0 nên miền nghiệm của bất phương trình x – y – 1 ≥ 0 là nửa mặt phẳng (kể cả bờ d₂) chứa điểm O(0; 0).

• Biểu diễn miền nghiệm của bất phương trình: x + 2y – 10 ≤ 0.

Vẽ đường thẳng d₃: x + 2y – 10 = 0 đi qua hai điểm (0; 5) và (10; 0).

Xét điểm O(0; 0) ∉ d₁, ta có: 0 + 2.0 – 10 = –10 < 0 nên miền nghiệm của bất phương trình x + 2y – 10 ≤ 0 là nửa mặt phẳng (kể cả bờ d₃) chứa điểm O(0; 0).

Miền không gạch chéo (kể cả bờ d₁, d₂, d₃) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

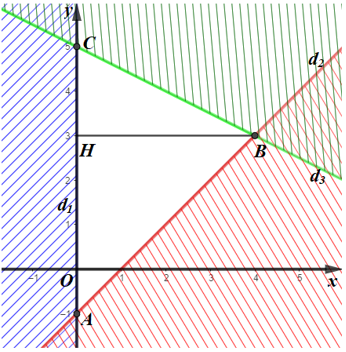
Miền nghiệm của hệ bất phương trình là miền tam giác ABC với A(–1; 0), B(4; 3) và C(0; 5).

Gọi BH là đường cao kẻ từ B đến AC.

Khi đó BH = |x_B| = 4.

CA = CO + OA = |y_C| + _|yA| = 5 + 1 = 6.

Diện tích của tam giác ABC là:

S = $\frac{1}{2}$BH.CA = $\frac{1}{2}$.4.6 = 12 (đơn vị diện tích).

Vậy ta chọn phương án B.

Câu 4. Một công ty kinh doanh thương mại chuẩn bị cho một đợt khuyến mại nhằm thu hút khách hàng bằng cách tiến hành quảng cáo sản phẩm của công ty trên hệ thống phát thanh và truyền hình. Chi phí cho 30 giây quảng cáo trên sóng phát thanh là 5 000 000 đồng, trên đài truyền hình là 15 000 000 đồng. Sóng phát thanh chỉ nhận phát các chương trình quảng cáo có thời lượng ít nhất là 30 giây và nhiều dài nhất 2 phút. Đài truyền hình chỉ nhận các chương trình quảng cáo có thời lượng ít nhất là 10 giây và nhiều nhất là 30 giây. Theo các phân tích, cùng thời lượng một phút quảng cáo, trên truyền hình sẽ có hiệu quả gấp 6 lần trên sóng phát thanh. Công ty dự định chi tối đa 20 000 000 đồng cho quảng cáo. Công ty cần đặt thời lượng quảng cáo trên sóng phát thanh và truyền hình như thế nào để hiệu quả nhất?

A. 30 giây trên sóng phát thanh và 10 giây đài truyền hình;

B. 30 giây trên sóng phát thanh và 30 giây đài truyền hình;

C. 90 giây trên sóng phát thanh và 10 giây đài truyền hình;

D. 120 giây trên sóng phát thanh và 10 giây đài truyền hình.

Hướng dẫn giải

Đáp án: B

Giải thích:

Chi phí cho 30 giây quảng cáo trên sóng phát thanh là 5 000 000 đồng, trên sóng truyền hình là 15 000 000 đồng nên chi phí cho 1 phút quảng cáo trên sóng phát thanh là 10 000 000 đồng, trên sóng truyền hình là 30 000 000 đồng.

Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh là x (phút), trên truyền hình là y (phút).

Chi phí cho quảng cáo trên sóng phát thanh là: 10 000 000x (đồng).

Chi phí cho quảng cáo trên truyền hình là: 30 000 000y (đồng).

Tổng chi phí cho việc quảng cáo là: 10 000 000x + 30 000 000y (đồng).

Do công ty dự định chi tối đa 20 000 000 đồng cho quảng cáo nên ta có:

10 000 000x + 30 000 000y ≤ 20 000 000

Hay x + 3y ≤ 2$\iff$ x + 3y – 2 ≤ 0.

Đổi 10 giây = $\frac{1}{6}$ phút, 30 giây = $\frac{1}{2}$ phút.

Sóng phát thanh chỉ nhận phát các chương trình quảng cáo có thời lượng ít nhất là 30 giây và nhiều dài nhất 2 phút nên ta có:

$\frac{1}{2}$ ≤ x ≤ 2 $\iff \left\{\begin{array}{l}x\ge \frac{1}{2}\\ x\le 2\end{array}\right.\iff \left\{\begin{array}{l}x-\frac{1}{2}\ge 0\\ x-2\le 0\end{array}\right.$

Đài truyền hình chỉ nhận các chương trình quảng cáo có thời lượng ít nhất là 10 giây và nhiều nhất là 30 giây nên ta có:

$\frac{1}{6}$ ≤ y ≤ $\frac{1}{2}$ $\iff \left\{\begin{array}{l}y\ge \frac{1}{6}\\ y\le \frac{1}{2}\end{array}\right.\iff \left\{\begin{array}{l}y-\frac{1}{6}\ge 0\\ y-\frac{1}{2}\le 0\end{array}\right.$

Hiệu quả chung của quảng cáo là: x + 6y.

Bài toán trở thành: Xác định x, y sao cho F(x; y) = x + 6y đạt giá trị lớn nhất với:

$\left\{\begin{array}{l}x-\frac{1}{2}\ge 0\\ x-2\le 0\\ y-\frac{1}{6}\ge 0\\ y-\frac{1}{2}\le 0\\ x+3y-2\le 0\end{array}\right.$

Biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng Oxy:

• Miền nghiệm của bất phương trình x – $\frac{1}{2}$ ≥ 0 là nửa mặt phẳng (kể cả bờ d₁: x – $\frac{1}{2}$ = 0) không chứa điểm O(0; 0).

• Miền nghiệm của bất phương trình x – 2 ≤ 0 là nửa mặt phẳng (kể cả bờ d₂: x – 2 = 0) chứa điểm O(0; 0).

• Miền nghiệm của bất phương trình y – $\frac{1}{2}$ ≥ 0 là nửa mặt phẳng (kể cả bờ d₃: y – $\frac{1}{6}$= 0) không chứa điểm O(0; 0).

• Miền nghiệm của bất phương trình y – $\frac{1}{2}$ ≤ 0 là nửa mặt phẳng (kể cả bờ d₄: y – $\frac{1}{2}$ = 0) chứa điểm O(0; 0).

• Miền nghiệm của bất phương trình x + 3y – 2 ≤ 0 là nửa mặt phẳng (kể cả bờ d₅: x + 3y – 2 = 0) chứa điểm O(0; 0).

Miền không gạch chéo (kể cả bờ d₁, d₂, d₃, d₄ và d₅) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

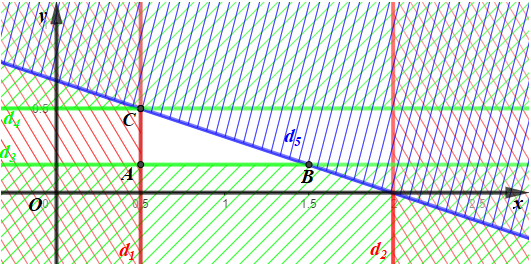
Miền nghiệm của hệ bất phương trình là miền tam giác ABC với A$\left(\frac{1}{2};\frac{1}{6}\right),$ B$\left(\frac{3}{2};\frac{1}{6}\right)$ và C$\left(\frac{1}{2};\frac{1}{2}\right).$ 

Xét F(x; y) = x + 6y ta có:

Tại A$\left(\frac{1}{2};\frac{1}{6}\right),$ F = $\frac{1}{2}+6.\frac{1}{6}=1,5;$ 

Tại B$\left(\frac{3}{2};\frac{1}{6}\right):$ F = $\frac{3}{2}+6.\frac{1}{6}=2,5;$ 

Tại C$\left(\frac{1}{2};\frac{1}{2}\right):$ F = $\frac{1}{2}+6.\frac{1}{2}=3,5.$ 

Khi đó F(x; y) đạt giá trị lớn nhất bằng 3,5 tại C$\left(\frac{1}{2};\frac{1}{2}\right).$ 

Tức là công ty đó cần đặt thời lượng trên đài phát thanh $\frac{1}{2}$ phút = 30 giây và trên đài truyền hình $\frac{1}{2}$ phút = 30 giây để đạt hiệu quả nhất.

Vậy ta chọn phương án B.

Câu 5. Nhân dịp tết Trung Thu, xí nghiệp sản xuất bánh muốn sản xuất hai loại bánh: Đậu xanh, Bánh dẻo nhân đậu xanh. Để sản xuất hai loại bánh này, xí nghiệp cần các nguyên liệu: đường, đậu xanh, bột, trứng, mứt, … Giả sử số đường có thể chuẩn bị được là 300 kg, đậu xanh là 200 kg, các nguyên liệu khác bao nhiêu cũng có. Sản xuất một cái bánh đậu xanh cần 0,03 kg đường, 0,04 kg đậu xanh và cho lãi 5 000 đồng. Sản xuất một cái bánh dẻo cần 0,07 kg đường, 0,04 kg đậu xanh và cho lãi 4 500 đồng. Cần lập kế hoạch để sản xuất mỗi loại bánh bao nhiêu cái để không bị động về đường, đậu và tổng số lãi thu được là lớn nhất (nếu sản xuất bao nhiêu cũng bán hết)?

A. 5 000 bánh đậu xanh và 0 bánh dẻo;

B. 1 250 bánh đậu xanh và 3 750 bánh dẻo;

C. 0 bánh đậu xanh và 4 000 bánh dẻo;

D. 0 bánh đậu xanh và 5 000 bánh dẻo.

Hướng dẫn giải

Đáp án: A

Giải thích:

Giả sử xí nghiệp sản xuất x (cái) bánh đậu xanh và y (cái) bánh dẻo nhân đậu xanh (x ≥ 0, y ≥ 0).

Sản xuất một cái bánh đậu xanh cần 0,03 kg đường, 0,04 kg đậu xanh nên để sản xuất x (cái) bánh đậu xanh thì cần 0,03x (kg) đường và 0,04x (kg) đậu xanh.

Sản xuất một cái bánh dẻo cần 0,07 kg đường, 0,04 kg đậu xanh nên để sản xuất y (cái) bánh dẻo thì cần 0,07y (kg) đường và 0,04y (kg) đậu xanh.

Số đường mà xí nghiệp có thể chuẩn bị được là 300 kg nên ta có:

0,03x + 0,07y ≤ 300 $\iff$ 3x + 7y – 30 000 ≤ 0.

Đậu xanh mà xí nghiệp có thể chuẩn bị được là 200 kg nên ta có:

0,04x + 0,04y ≤ 200 $\iff$ x + y – 5 000 ≤ 0.

Bán được hết x (cái) bánh đậu xanh và y (cái) bánh dẻo thì xí nghiệp thu được số tiền lãi là: F(x; y) = 5 000x + 4 500y.

Bài toán trở thành: Xác định x, y sao cho F(x; y) = 5 000x + 4 500y đạt giá trị lớn nhất với: $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ 3x+7y-30000\le 0\\ x+y-5000\le 0.\end{array}\right.$

Biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng Oxy:

• Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng (kể cả bờ d₁: x = 0) chứa điểm (1; 1).

• Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng (kể cả bờ d₂: y = 0) chứa điểm (1; 1).

• Miền nghiệm của bất phương trình 3x + 7y – 30 000 ≤ 0 là nửa mặt phẳng (kể cả bờ d₃: 3x + 7y – 30 000 = 0) chứa điểm (1; 1).

• Miền nghiệm của bất phương trình x + y – 5 000 ≤ 0 là nửa mặt phẳng (kể cả bờ d₄: x + y – 5 000 = 0) chứa điểm (1; 1).

Miền không gạch chéo (kể cả bờ d₁, d₂, d₃, d₄) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

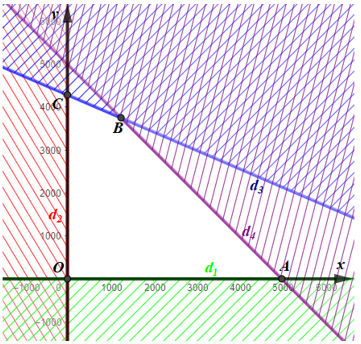
Miền nghiệm của hệ bất phương trình là miền tứ giác OABC với O(0; 0), A(5 000; 0), B(1 250; 3 750) và C(0; 4 000).

Xét biểu thức F(x; y) = 5 000x + 4 500y, ta có:

• Tại O(0; 0):

F = 5 000.0 + 4 500.0 = 0;

• Tại A(5 000; 0):

F = 5 000 . 5 000 + 4 500.0 = 25 000 000;

• Tại B(1 250; 3 750):

F = 5 000 .1 250 + 4 500 .3 750 = 23 125 000;

• Tại C(0; 4 000):

F = 5 000.0 + 4 500 . 4 000 = 18 000 000.

Khi đó F(x; y) đạt giá trị lớn nhất bằng 25 000 000 tại A(5 000; 0).

Vậy xí nghiệp cần sản xuất 5 000 cái bánh đậu xanh và không sản xuất bánh dẻo.

Ta chọn phương án A.

Xem thêm các bài trắc nghiệm Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Trắc nghiệm Bài 1: Bất phương trình bậc nhất hai ẩn

Trắc nghiệm Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Trắc nghiệm Ôn tập chương 2

Trắc nghiệm Bài 1: Hàm số và đồ thị

Trắc nghiệm Bài 2: Hàm số bậc hai