Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Chuyên đề trắc nghiệm Hàm số bậc nhất và bậc hai – có đáp án chi tiết
Chuyên đề hàm số bậc nhất và bậc hai
Câu 110. [0D2-1] Trục đối xứng của parabol \(y = – {x^2} + 5x + 3\) là đường thẳng có phương trình
A. \(x = \frac{5}{4}\).
B. \(x = – \frac{5}{2}\).
C. \(x = – \frac{5}{4}\).
D. \(x = \frac{5}{2}\).
Lời giải
Chọn D.
Trục đối xứng của parabol \(y = a{x^2} + bx + c\) là đường thẳng \(x = – \frac{b}{{2a}}\).
Trục đối xứng của parabol \(y = – {x^2} + 5x + 3\) là đường thẳng \(x = \frac{5}{2}\).
Câu 111. [0D2-1] Hàm số \(f(x) = (m – 1)x + 2m + 2\) là hàm số bậc nhất khi và chỉ khi
A. \(m \ne – 1\).
B. \(m > 1\).
C. \(m \ne 1\).
D. \(m \ne 0\).
Chọn C.
Lời giải
Hàm số \(f(x) = (m – 1)x + 2m + 2\) là hàm số bậc nhất khi và chỉ khi \(m – 1 \ne 0 \Leftrightarrow m \ne 1\).
Câu 112. [0D2-1] Điểm nào sau đây thuộc đồ thị của hàm số \(y = \frac{{x – 2}}{{x(x – 1)}}\)
A. \(M(0; – 1)\).
B. \(M(2;1)\).
C. \(M(2;0)\).
D. \(M(1;1)\).
Lời giải
Chọn C.
Thử trực tiếp thấy tọa độ của \(M(2;0)\) thỏa mãn phương trình hàm số.
Câu 113. [0D2-1] Hệ số góc của đồ thị hàm số \(y = 2018x – 2019\) bằng
A. \( – \frac{{2019}}{{2018}}\).
B. 2018 .
C. \( – 2019\).
D. \( – \frac{{2018}}{{2019}}\).
Lời giải
Chọn B.
Câu 114. [0D2-1] Hàm số \(y = {x^4} – {x^2} + 3\) là
A. Hàm số vừa chã̃n, vừa lẻ.
B. Hàm số không chã̃n, không lẻ.
C. Hàm số lẻ.
D. Hàm số chẵn.
Lời giải
Chọn D.
Đặt \(f(x) = {x^4} – {x^2} + 3\)
Ta có \(f( – x) = {( – x)^4} – {( – x)^2} + 3 = {x^4} – {x^2} + 3 = f(x)\)
Vậy hàm số đã cho là hàm số chã̃n.
Câu 115. [0D2-1] Tập xác định của hàm số \(y = \frac{{2 – x}}{{{x^2} – 4x}}\) là
A. \(\mathbb{R}\backslash \{ 0;2;4\} \).
B. \(\mathbb{R}\backslash [0;4]\).
C. \(\mathbb{R}\backslash (0;4)\).
D. \(\mathbb{R}\backslash \{ 0;4\} \).
Chọn D.
Lời giải
Hàm số xác định \( \Leftrightarrow {x^2} – 4x \ne 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 0}\\{x \ne 4}\end{array}} \right.\). Vậy \(D = \mathbb{R}\backslash \{ 0;4\} \).
Câu 116. [0D2-1] Cho hàm số \(f(x) = {x^2} – |x|\). Khẳng định nào sau đây là đúng?
A. Đồ thị của hàm số \(f(x)\) đối xứng qua trục hoành.
B. Đồ thị của hàm số \(f(x)\) đối xứng qua gốc tọa độ.
C. \(f(x)\) là hàm số lẻ.
D. \(f(x)\) là hàm số chẵn.
Lời giải
Chọn D.
Tập xác định \(D = \mathbb{R}\).
Ta có \(f( – x) = {( – x)^2} – | – x| = {x^2} – |x| = f(x)\).
Vậy \(f(x)\) là hàm số chẵn.
Câu 117. [0D2-1] Tìm tập xác định D của hàm số \(f(x) = \sqrt {x + 1} + \frac{1}{x}\).
A. \(D = \mathbb{R}\backslash \{ 0\} \).
B. \(D = [1; + \infty )\).
C. \(D = \mathbb{R}\backslash \{ – 1;0\} \).
D. \(D = [ – 1; + \infty )\backslash \{ 0\} \).
Lời giải
Chọn D.
Điều kiện: \(\left\{ {\begin{array}{*{20}{l}}{x + 1 \ge 0}\\{x \ne 0}\end{array}} \right.\).
Vậy tập xác định của hàm số là \(D = [ – 1; + \infty )\backslash \{ 0\} \).
Câu 118. [0D2-1] Cho hàm số \(y = f(x)\) xác định trên tập D. Mệnh đề nào sau đây đúng?
A. Nếu \(f(x)\) không là hàm số lẻ thì \(f(x)\) là hàm số chã̃n.
B. Nếu \(f( – x) = – f(x),\forall x \in D\) thì \(f(x)\) là hàm số lẻ.
C. Đồ thị hàm số lẻ nhận trục tung làm trục đối xứng.
D. Nếu \(f(x)\) là hàm số lẻ thì \(f( – x) = – f(x),\forall x \in D\).
Lời giải
Chọn D.
A sai vì có những hàm số không chăn, không lẻ.
B sai vì \(f(x) = 0\) thì \(f( – x) = – f(x)\) nhưng \(f(x)\) cũng là hàm số chẵn.
C sai vì đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
Câu 119. [0D2-1] Cho hàm số bậc hai \(y = a{x^2} + bx + c(a \ne 0)\) có đồ thị \((P)\), đỉnh của \((P)\) được xác định bởi công thức nào?
A. \(I\left( { – \frac{b}{{2a}}; – \frac{\Delta }{{4a}}} \right)\).
B. \(I\left( { – \frac{b}{a}; – \frac{\Delta }{{4a}}} \right)\).
C. \(I\left( {\frac{b}{a};\frac{\Delta }{{4a}}} \right)\).
D. \(I\left( { – \frac{b}{{2a}}; – \frac{\Delta }{{2a}}} \right)\).
Lời giải
Chọn A.
Đỉnh của parabol \((P):y = a{x^2} + bx + c(a \ne 0)\) là điểm \(I\left( { – \frac{b}{{2a}}; – \frac{\Delta }{{4a}}} \right)\).
Câu 120. [0D2-1] Cho hàm số \(y = a{x^2} + bx + c(a > 0)\). Khẳng định nào sau đây là sai?
A. Đồ thị của hàm số có trục đối xứng là đường thẳng \(x = – \frac{b}{{2a}}\).
B. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt.
C. Hàm số đồng biến trên khoảng \(\left( { – \frac{b}{{2a}}; + \infty } \right)\).
D. Hàm số nghịch biến trên khoảng \(\left( { – \infty ; – \frac{b}{{2a}}} \right)\).
Lời giải
Chọn B.
Dựa vào sự biến thiên của hàm số \(y = a{x^2} + bx + c(a > 0)\) ta thấy các khẳng định A,C,D đúng Khẳng định \({\rm{B}}\) sai vì có những hàm số bậc hai không cắt trục hoành như hàm \(y = – 2{x^2} + 3x – \frac{9}{8}\)
Câu 121. [0D2-1] Phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) có hai nghiệm phân biệt cùng dấu khi và chỉ khi:
A. \(\left\{ {\begin{array}{*{20}{l}}{\Delta > 0}\\{P > 0}\end{array}} \right.\).
B. \(\left\{ {\begin{array}{*{20}{l}}{\Delta > 0}\\{S < 0}\end{array}} \right.\).
C. \(\left\{ {\begin{array}{*{20}{l}}{\Delta \ge 0}\\{P > 0}\end{array}} \right.\).
D. \(\left\{ {\begin{array}{*{20}{l}}{\Delta > 0}\\{S > 0}\end{array}} \right.\).
Lời giải
Chọn A.
Phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) có hai nghiệm phân biệt cùng dấu khi và chỉ \(\left\{ {\begin{array}{*{20}{l}}{\Delta > 0}\\{P > 0}\end{array}} \right.\).
Câu 122. [0D2-1] Tìm tập xác định D của hàm số \(f(x) = \sqrt {x + 1} + \frac{1}{x}\).
A. \(D = \mathbb{R}\backslash \{ 0\} \).
B. \(D = \mathbb{R}\backslash \{ – 1;0\} \).
C. \(D = [ – 1; + \infty )\backslash \{ 0\} \).
D. \(D = [ – 1; + \infty )\).
Lời giải
Chọn C.
Điều kiện xác định: \(\left\{ {\begin{array}{*{20}{l}}{x + 1 \ge 0}\\{x \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge – 1}\\{x \ne 0}\end{array}} \right.} \right.\). Vậy tập xác định: \(D = [ – 1; + \infty )\backslash \{ 0\} \).
Câu 123. [0D2-1] Đường thẳng nào sau đây song song với đường thẳng \(y = \sqrt 2 x\) ?
A. \(y = \frac{2}{{\sqrt 2 }}x – 5\).
B. \(y = 1 – \sqrt 2 x\).
C. \(y = \frac{1}{{\sqrt 2 }}x – 3\).
D. \(y = – \sqrt 2 x + 2\).
Lời giải
Chọn A.
Hai đường thẳng song song khi hai hệ số góc bằng nhau.
Câu 124. [0D2-1] Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng?
A. \(a > 0,b < 0,c < 0\).
B. \(a > 0,b < 0,c > 0\).
C. \(a > 0,b > 0,c > 0\).
D. \(a < 0,b < 0,c < 0\).
Lời giải
Chọn A.
Parabol có bề lõm quay lên \( \Rightarrow a > 0\) loại D.
Parabol cắt trục tung tại điểm có tung độ âm nên \(c < 0\) loại B,C. Chọn A.
Câu 125. [0D2-1] Parabol \(y = – {x^2} + 2x + 3\) có phương trình trục đối xứng là
A. \(x = – 1\).
B. \(x = 2\).
C. \(x = 1\).
D. \(x = – 2\).
Chọn C.
Parabol \(y = – {x^2} + 2x + 3\) có trục đối xứng là đường thẳng \(x = – \frac{b}{{2a}} \Leftrightarrow x = 1\).
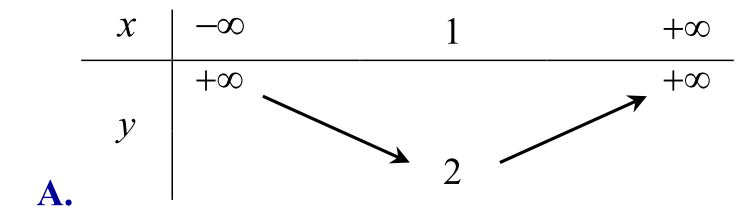
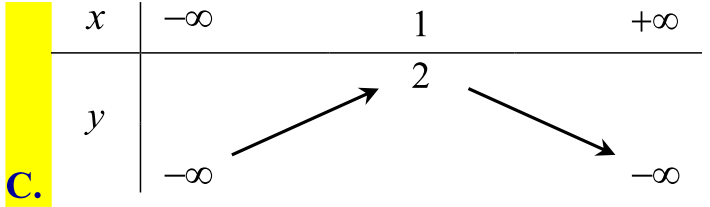
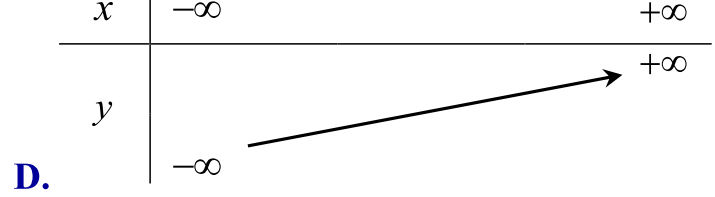
Câu 126. [0D2-1] Bảng biến thiên nào dưới đây là của hàm số \(y = – {x^2} + 2x + 1\) :

Lời giải
Chọn C.
Xét hàm số \(y = – {x^2} + 2x + 1\) có \(a = – 1 < 0\), tọa độ đỉnh \(I(1;2)\) do đó hàm số trên tăng trên khoảng \(( – \infty ;1)\) và giảm trên khoảng \((1; + \infty )\).
Câu 127. [0D2-1] Khẳng định nào về hàm số \(y = 3x + 5\) là sai:
A. Hàm số đồng biến trên \(\mathbb{R}\).
B. Đồ thị cắt Ox tại \(\left( { – \frac{5}{3};0} \right)\).
C. Đồ thị cắt Oy tại \((0;5)\).
D. Hàm số nghịch biến trên \(\mathbb{R}\).
Lời giải
Chọn D.
Hàm số \(y = 3x + 5\) có hệ số \(a = 3 > 0\) nên đồng biến trên \(\mathbb{R}\), suy ra đáp án D sai.
Câu 128. [0D2-1] Cho hàm số: \(y = \left\{ {\begin{array}{*{20}{c}}{\frac{1}{{x – 1}}}&{x \le 0}\\{\sqrt {x + 2} }&{x > 0}\end{array}} \right.\). Tập xác định của hàm số là tập hợp nào sau đây?
A. \([ – 2; + \infty )\).
B. \(\mathbb{R}\).
C. \(\mathbb{R}\backslash \{ 1\} \).
D. \(\{ x \in \mathbb{R}\backslash x \ne 1\) và \(x \ge – 2\} \).
Lời giải
Chọn B.
Với \(x \le 0\) ta có: \(y = \frac{1}{{x – 1}}\) xác định với mọi \(x \ne 1\) nên xác định với mọi \(x \le 0\).
Với \(x > 0\) ta có: \(y = \sqrt {x + 2} \) xác định với mọi \(x \ge – 2\) nên xác định với mọi \(x > 0\).
Vậy tập xác định của hàm số là \(D = \mathbb{R}\).
Câu 129. [0D2-1] Cho hàm số: \(y = {x^2} – 2x – 1\), mệnh đề nào sai:
A. Đồ thị hàm số nhận \(I(1; – 2)\) làm đỉnh.
B. Hàm số nghịch biến trên khoảng \(( – \infty ;1)\).
C. Hàm số đồng biến trên khoảng \((1; + \infty )\).
D. Đồ thị hàm số có trục đối xứng: \(x = – 2\).
Lời giải
Chọn D.
Trục đối xứng của đồ thị hàm số là đường thẳng \(x = – \frac{b}{{2a}} = 1\).
Câu 130. [0D2-1] Tập xác định của hàm số \(y = \frac{{\sqrt {x + 1} }}{{x – 3}}\) là
A. \((3; + \infty )\).
B. \([1; + \infty )\).
C. \([ – 1;3) \cup (3; + \infty )\).
D. \(\mathbb{R}\backslash \{ 3\} \).
Lời giải
Chọn C.
Hàm số \(y = \frac{{\sqrt {x + 1} }}{{x – 3}}\).
Điều kiện xác định: \(\left\{ {\begin{array}{*{20}{l}}{x + 1 \ge 0}\\{x – 3 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge – 1}\\{x \ne 3}\end{array}} \right.} \right.\).
Vậy tập xác định của hàm số \(D = [ – 1;3) \cup (3; + \infty )\).
Câu 131. [0D2-1] Tìm m để hàm số \(y = (3 – m)x + 2\) nghịch biến trên \(\mathbb{R}\).
A. \(m > 0\).
B. \(m = 3\).
C. \(m > 3\).
D. \(m < 3\).
ChọnC.
Lời giải
Hàm số \(y = (3 – m)x + 2\) có dạng hàm số bậc nhất.
Để hàm số nghịch biến trên \(\mathbb{R}\) thì \(3 – m < 0 \Leftrightarrow m > 3\).
Câu 132. [0D2-1] Parabol \((P):y = – 2{x^2} – 6x + 3\) có hoành độ đỉnh là?
A. \(x = – 3\).
B. \(x = \frac{3}{2}\).
C. \(x = – \frac{3}{2}\).
D. \(x = 3\).
Lời giải
Chọn A.
Hoành độ đỉnh của parabol \((P)\) là: \(x = \frac{{ – b}}{{2a}} = \frac{6}{{ – 4}} = – \frac{3}{2}\).
Câu 133. [0D2-1] Hàm số nào sau đây có tập xác định là \(\mathbb{R}\) ?
A. \(y = \frac{{3x}}{{{x^2} – 4}}\)
B. \(y = {x^2} – 2\sqrt {x – 1} – 3\).
C. \(y = {x^2} – \sqrt {{x^2} + 1} – 3\).
D. \(y = \frac{{2\sqrt x }}{{{x^2} + 4}}\).
Lời giải
Chọn C.
Dễ thấy hàm số \(y = {x^2} – \sqrt {{x^2} + 1} – 3\) có tập xác định là \(\mathbb{R}\).
Xem thêm