Giải bài tập Toán lớp 10 Bài 11: Tích vô hướng của hai vecto
1. Góc giữa hai vectơ
Giải Toán 10 trang 66 Tập 1 Kết nối tri thức
HĐ1 trang 66 Toán lớp 10: Trong hình 4.39, số đo góc BAC cũng được gọi là số đo góc giữa hai vectơ và . Hãy tìm số đo các góc giữa và , và .
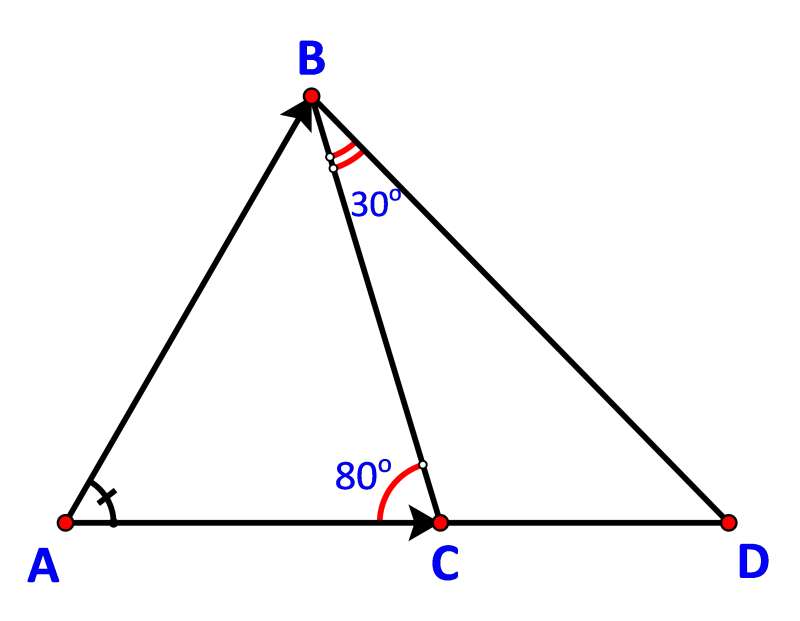
Lời giải:
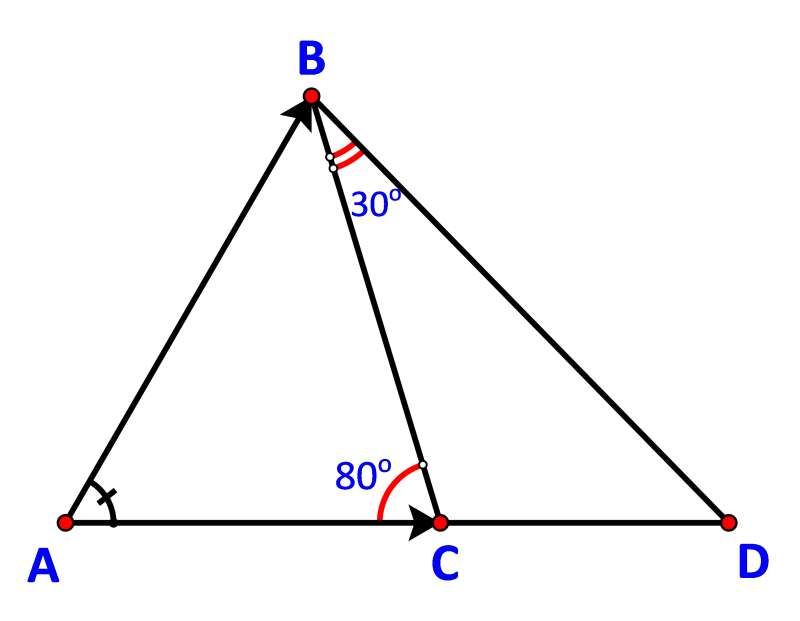
Góc giữa hai vectơ và là góc CBD và số đo .
Góc giữa hai vectơ và là góc ADB.
Ta có: (tính chất góc ngoài)
Vậy số đo góc giữa hai vectơ và , và lần lượt là
Câu hỏi trang 66 Toán lớp 10: Khi nào thì góc giữa hai vectơ bằng , bằng
Phương pháp giải:
Cách xác định góc giữa hai vecto
Lấy điểm A bất kì vẽ , khi đó
Lời giải:
Góc giữa hai vectơ bằng nếu chúng cùng hướng
Góc giữa hai vectơ bằng nếu chúng ngược hướng.
Luyện tập 1 trang 66 Toán lớp 10: Cho tam giác đều ABC. Tính .
Phương pháp giải:
Lấy D sao cho: .
Khi đó:
Lời giải:
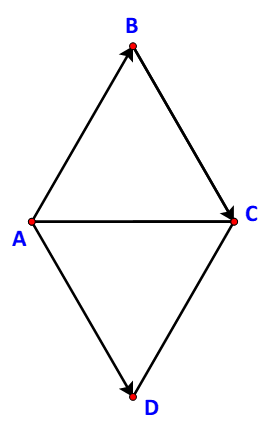
Lấy điểm D sao cho:
Khi đó ta có:
Dễ thấy ABCD là hình bình hành (hơn nữa còn là hình thoi) nên
Vậy số đo góc là .
2. Tích vô hướng của hai vectơ
Giải Toán 10 trang 67 Tập 1 Kết nối tri thức
Câu hỏi 1 trang 67 Toán lớp 10: Khi nào thì tích vô hướng của hai vectơ là một số dương? Là một số âm?
Phương pháp giải:
+) Tích vô hướng của hai vectơ :
Nhận xét: cùng dấu với
Lời giải:
Dễ thấy: cùng dấu với (do ). Do đó:
+) hay
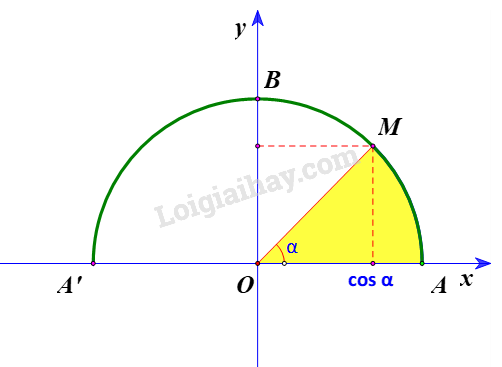
+) hay
Vậy nếu và nếu
Câu hỏi 2 trang 67 Toán lớp 10: Khi nào thì ?
Phương pháp giải:
+)
+) với mọi vectơ
Lời giải:
Hay hai vectơ cùng phương.
Vậy hai vectơ cùng phương thì
Luyện tập 2 trang 67 Toán lớp 10: Cho tam giác AB C có BC = a, CA = b, AB = c. Hãy tính theo a,b,c.
Phương pháp giải:
+) Tích vô hướng:
Lời giải:
Ta có:
Mà
Lại có: (suy ra từ định lí cosin)
3. Biểu thức tọa độ và tính chất của tích vô hướng
Giải Toán 10 trang 68 Tập 1 Kết nối tri thức
HĐ2 trang 68 Toán lớp 10: Cho hai vectơ cùng phương và . Hãy kiểm tra công thức theo từng trường hợp sau:
a)
b) và
c) và
Phương pháp giải:
Tính tích vô hướng bằng công thức:
Lời giải:
a) Vì nên vuông góc với mọi .
Như vậy
Mặt khác:
b) Vì và nên và cùng hướng.
(|k|= k do k > 0)
c) Vì và nên và ngược hướng.
HĐ3 trang 68 Toán lớp 10: Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương và .
a) Xác định tọa độ của các điểm A và B sao cho
b) Tính theo tọa độ của A và B.
c) Tính theo tọa độ của A, B.
Lời giải:
a) Vì nên A(x; y).
Tương tự: do nên B (x’; y’)
b) Ta có:
Và
Lại có:
c) Theo định lí cosin trong tam giác OAB ta có:
Mà
Luyện tập 3 trang 68 Toán lớp 10: Tích vô hướng và góc giữa hai vectơ
Phương pháp giải:
Cho và , khi đó:
Lời giải:
Ta có:
HĐ4 trang 68 Toán lớp 10: Cho ba vectơ
a) Tính theo tọa độ của các vectơ
b) So sánh và
c) So sánh và
Phương pháp giải:
Cho và , khi đó:
Lời giải:
a) Ta có:
Và:
b) Vì
Nên
c) Ta có:
Giải Toán 10 trang 70 Tập 1 Kết nối tri thức
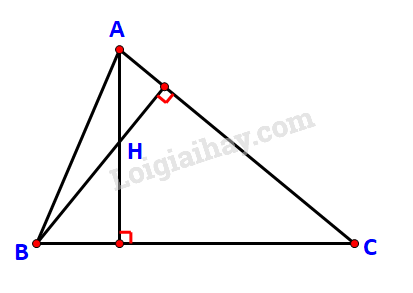
Luyện tập 4 trang 70 Toán lớp 10: Cho tam giác ABC với A(-1; 2), B(8; -1), C(8; 8). Gọi H là trực tâm của tam giác.
a) Chứng minh rằng và
b) Tìm tọa độ của H.
c) Giải tam giác ABC.
Phương pháp giải:
a)
b) Lập hệ PT biết và .
c) Nếu vectơ thì
Lời giải:
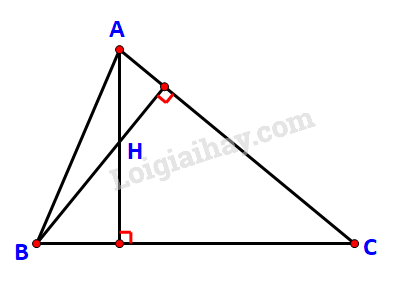
a) và
. Do đó
Tương tự suy ra .
b) Gọi H có tọa độ (x; y)
Ta có: và
Lại có: và
Vậy H có tọa độ (6; 2)
c) Ta có:
Và ;
Áp dụng định lí cosin cho tam giác ABC, ta có:
Vậy tam giác ABC có: ;
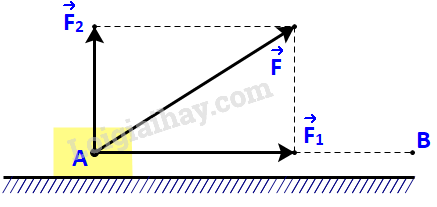
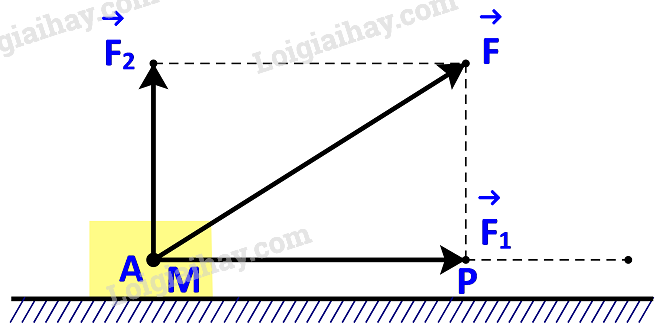
Vận dụng trang 70 Toán lớp 10: Một lực không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ A đến B. Lực được phân tích thành hai lực thành phần là và
a) Dựa vào tính chất của tích vô hướng, hãy giải thích vì sao công sinh bởi lực (đã được đề cập ở trên) bằng tổng của các công sinh bởi các lực và .
b) Giả sử các lực thành phần , tương ứng cùng phương, vuông góc với phương chuyển động của vật. Hãy tìm mối quan hệ giữa các công sinh bởi lực và lực .
Phương pháp giải:
Khi lực không đổi tác dụng lên một vật và điểm đặt chuyển dời một đoạn s theo hướng hợp với hướng của lực góc α thì công sinh bởi lực đó là:
Lời giải:
a)
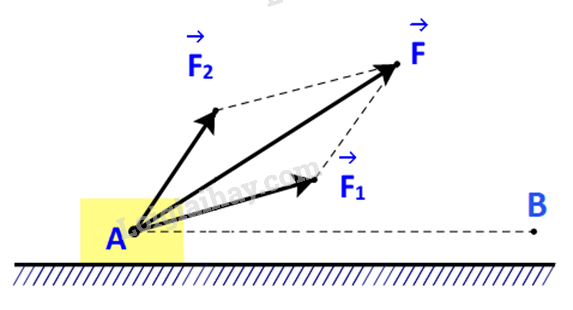
Gọi lần lượt là công sinh bởi lực , và .
Ta cần chứng minh:
Xét lực , công sinh bởi lực là:
Tương tự, ta có: ,
Áp dụng tính chất của tích vô hướng ta có:
b)
Vì tương ứng vuông góc với phương chuyển động nên
Do đó: công sinh bởi lực là:
Mà
Vậy công sinh bởi lực bằng công sinh bởi lực .
Bài tập
Bài 4.21 trang 70 Toán lớp 10: Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vectơ và trong mỗi trường hợp sau:
a)
b)
c)
Phương pháp giải:
Tính góc giữa hai vectơ dựa vào tích vô hướng:
Lời giải:
a)
hay .
b)
c) Dễ thấy: và cùng phương do
Hơn nữa: ;
Do đó: và ngược hướng.
Chú ý:
Khi tính góc, ta kiểm tra các trường hợp dưới đây trước:
+ : nếu
+ và cùng phương:
nếu và cùng hướng
nếu và ngược hướng
Nếu không thuộc các trường hợp trên thì ta tính góc dựa vào công thức
Bài 4.22 trang 70 Toán lớp 10: Tìm điều kiện của để:
a)
b)
Phương pháp giải:
Tích vô hướng
Lời giải:
a)
Ta có:
Nói cách khác: cùng hướng.
b)
Ta có:
Nói cách khác: ngược hướng.
Bài 4.23 trang 70 Toán lớp 10: Trong mặt phẳng tọa độ Oxy, cho hai điểm A (1; 2), B(-4; 3). Gọi M (t; 0) là một điểm thuộc trục hoành.
a) Tính theo t.
b) Tính t để
Phương pháp giải:
+) Nếu vecto và thì
+)
Lời giải:
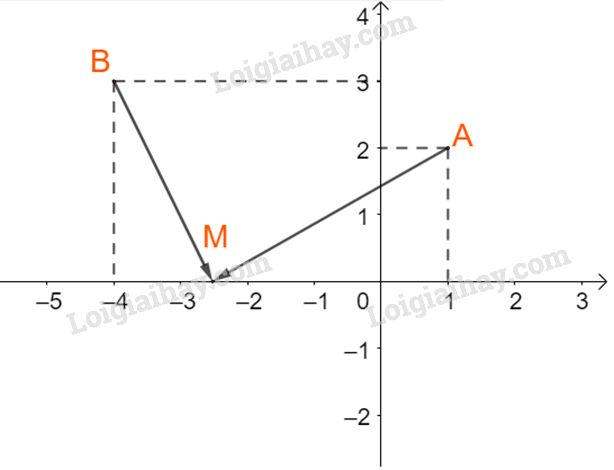
a)
Ta có: A (1; 2), B(-4; 3) và M (t; 0)
b)
Để hay thì
Vậy t = -1 hoặc t = -2 thì
Bài 4.24 trang 70 Toán lớp 10: Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A (-4; 1), B (2;4), C (2; -2)
a) Giải tam giác
b) Tìm tọa độ trực tâm H của tam giác ABC.
Phương pháp giải:
a) Độ dài vectơ là
b) Chỉ ra và từ đó tìm tọa độ của H.
Lời giải:
a) Ta có:
Áp dụng định lí cosin cho tam giác ABC, ta có:
Vậy tam giác ABC có: ;
b)
Gọi H có tọa độ (x; y)
Lại có: H là trực tâm tam giác ABC
và
và
Do đó và .
Mà:
Và
Vậy H có tọa độ
Bài 4.25 trang 70 Toán lớp 10: Chứng minh rằng với mọi tam giác ABC, ta có:
Phương pháp giải:
Biến đổi vế trái, đưa về công thức
+)
+) với mọi .
Lời giải:
Đặt
Mà
(Vì nên )
Do đó hay (đpcm)
Bài 4.26 trang 70 Toán lớp 10: Cho tam giác ABC có trọng tâm G. Chứng minh rằng với mọi điểm M, ta có:
Phương pháp giải:
+)
+) Với 3 điểm M, A, G bất kì ta có:
+) G là trọng tâm tam giác ABC thì:
Lời giải:
Ta có:
( do G là trọng tâm tam giác ABC)
(đpcm)
Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 10: Vectơ trong mặt phẳng tọa độ
Bài tập cuối chương 4
Bài 12: Số gần đúng và sai số
Bài 13: Các số đặc trưng đo trung tâm xu thế