Giải SGK Toán 10 Bài 19 (Kết nối tri thức): Phương trình đường thẳng

Giải bài tập Toán lớp 10 Bài 19: Phương trình đường thẳng

A. Câu hỏi

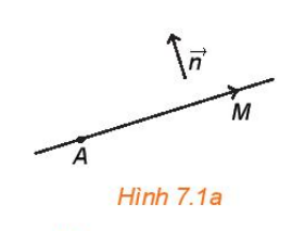
Hoạt động 1 trang 31 Toán 10 Tập 2: Cho vectơ $\overrightarrow{n}$ ≠$\overrightarrow{0}$ và điểm A. Tìm tập hợp những điểm M sao cho $\overrightarrow{AM}$ vuông góc với $\overrightarrow{n}$.

 

Lời giải:

Vẽ đường thẳng d đi qua điểm A sao cho đường thẳng d vuông góc với giá của vectơ $\overrightarrow{n}$.

Lấy điểm M thuộc đường thẳng d thì $\overrightarrow{AM}$ vuông góc với $\overrightarrow{n}$.

Vậy tập hợp những điểm M sao cho $\overrightarrow{AM}$ vuông góc với $\overrightarrow{n}$ là đường thẳng d đi qua điểm A và vuông góc với giá của vectơ $\overrightarrow{n}$.

Hoạt động 2 trang 31 Toán 10 Tập 2: Trong mặt phẳng toạ độ, cho đường thẳng ∆ đi qua điểm A(x0; y0) và có vectơ pháp tuyến $\overrightarrow{n}$(a; b). Chứng minh rằng điểm M(x; y) thuộc ∆ khi và chỉ khi

a(x – x0) + b(y – y0) = 0

Lời giải:

* Giả sử M(x; y) thuộc đường thẳng ∆, ta cần chứng minh: a(x – x0) + b(y – y0) = 0

Vì M ∈ ∆ nên $\overrightarrow{AM}\perp \overrightarrow{n}$

$\Rightarrow \overrightarrow{AM}$. $\overrightarrow{n}$ = 0

Mà $\overrightarrow{AM}$ = (x – x0; y – y0) và $\overrightarrow{n}$(a; b)

$\Rightarrow$ a(x – x0)  + b(y – y0) = 0 (đpcm) (1)

* Giả sử, với M(x; y) thỏa mãn a(x – x0) + b(y – y0) = 0; ta cần chứng minh M thuộc đường thẳng ∆

Theo giả thiết ta có: a(x – x0) + b(y – y0) = 0

Mà $\overrightarrow{AM}$ = (x – x0; y – y0) và $\overrightarrow{n}$(a; b)

Nên $\overrightarrow{AM}$. $\overrightarrow{n}$ = 0 hay $\overrightarrow{AM}\perp \overrightarrow{n}$

Do đó $\overrightarrow{n}$ là vectơ pháp tuyến của đường thẳng AM

Mặt khác $\overrightarrow{n}$ cũng là vectơ pháp tuyến của đường thẳng ∆

Suy ra đường thẳng AM và đường thẳng ∆ có giá song song hoặc trùng nhau.

Vì đường thẳng ∆ đi qua A nên đường thẳng AM trùng ∆.

Hay điểm M cũng thuộc đường thẳng ∆ (đpcm) (2)

Từ (1) và (2) ta có: điểm M(x; y) thuộc ∆ khi và chỉ khi a(x – x0) + b(y – y0) = 0.

Luyện tập 1 trang 32 Toán 10 Tập 2: Trong mặt phẳng toạ độ , cho tam giác có 3 đỉnh A(-1; 5) , B( 2; 3), C(6; 1). Lập phương trình tổng quát của đường cao kẻ từ A của tam giác ABC.

Lời giải:

Gọi H là chân đường cao kẻ từ điểm A xuống BC.

Do đó: AH ⊥ BC hay ta có đường thẳng AH nhận $\overrightarrow{BC}$ làm vectơ pháp tuyến.

Ta có $\overrightarrow{BC}$= (4 ; -2)

Lấy $\overrightarrow{n}$= $\frac{1}{2}\overrightarrow{BC}$= (2 ; -1). Khi đó $\overrightarrow{n}$ cũng là một vectơ pháp tuyến của đường thẳng AH.

Phương trình đường thẳng AH đi qua A(-1; 5) và nhận $\overrightarrow{n}$= (2 ; -1) làm VTPT là:

2.[x – (-1)] – 1.(y – 5) = 0

 ⇔ 2x + 2 – y + 5  = 0 hay 2x – y + 7 = 0.

Vậy phương trình đường cao kẻ từ A của tam giác ABC là: 2x – y + 7 = 0.

Luyện tập 2 trang 32 Toán 10 Tập 2: Hãy chỉ ra một vectơ pháp tuyến của đường thẳng ∆ : y = 3x + 4.

Lời giải:

Theo giả thiết ta có phương trình đường thẳng ∆ có dạng y = 3x + 4 hay 3x – y + 4 = 0

Vậy vectơ pháp tuyến của ∆ là $\overrightarrow{n}$(3; -1).

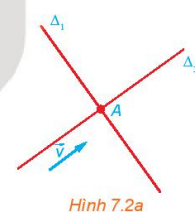
Hoạt động 3 trang 32 Toán 10 Tập 2: Trong Hình 7.2a , nếu một vật thể chuyển động với vectơ vận tốc bằng $\overrightarrow{v}$và nó đi qua điểm A thì nó di chuyển trên đường nào?

 

Lời giải:

Ta có $\overrightarrow{v}$ có giá song song với đường thẳng ∆2 và điểm A thuộc đường thẳng ∆2 nên nếu một vật thể chuyển động với vectơ vận tốc bằng $\overrightarrow{v}$và nó đi qua điểm A thì nó di chuyển trên đường ∆2.

Luyện tập 3 trang 33 Toán 10 Tập 2: Hãy chỉ ra một vectơ chỉ phương của đường thẳng ∆ : 2x – y + 1 = 0.

Lời giải:

Xét phương trình đường thẳng ∆ : 2x – y + 1 = 0 ta có vectơ pháp tuyến $\overrightarrow{n}$(2; -1)

Vậy vectơ chỉ phương $\overrightarrow{u}$(1; 2).

Hoạt động 4 trang 33 Toán 10 Tập 2: Chuyển động của một vật thể được thể hiện trên mặt phẳng Oxy. Vật thể khởi hành từ A(2; 1) và chuyển động thẳng đều với vận tốc $\overrightarrow{v}$(3; 4).

a) Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm đi qua và vectơ chỉ phương của đường thẳng đó).

b) Chứng minh rằng tại thời điểm t (t > 0) tính từ khi khởi hành, vật thể ở vị trí có toạ độ là (2 + 3t; 1 + 4t).

Lời giải:

a) Vật thể sẽ chuyển động trên đường thẳng đi qua A và song song hoặc trùng với giá vectơ vận tốc $\overrightarrow{v}$(3; 4)

Hay đường thẳng đi qua điểm A và có vectơ chỉ phương là $\overrightarrow{v}$(3; 4).

b) Gọi B(x; y) là vị trí của vật thể tại thời điểm t (t > 0).

Vật thể đó chuyển động từ A đến B, nghĩa là quãng đường đi được là AB có thể xem là vectơ vận tốc là vectơ  $\overrightarrow{AB}$.

Quãng đường AB bằng độ lớn vận tốc nhân thời gian nên ta có: AB = t.$\left|\overrightarrow{v}\right|$ mà vectơ  $\overrightarrow{AB}$ cùng hướng với $\overrightarrow{v}$ nên $\overrightarrow{AB}$= t .$\overrightarrow{v}$.

Ta có: $\overrightarrow{AB}$ = (x – 2; y – 1)

⇒ (x – 2; y – 1) = (3t; 4t)

⇒ $\left\{\begin{array}{l}x-2=3t\\ y-1=4t\end{array}\right.$

⇔$\left\{\begin{array}{l}x=2+3t\\ y=1+4t\end{array}\right.$

Vậy toạ độ B(2 + 3t; 1+4t) là vị trí của vật thể tại thời điểm t(t > 0).

Luyện tập 4 trang 33 Toán 10 Tập 2: Lập phương trình tham số của đường thẳng ∆ đi qua điểm M(-1; 2) và song song với đường thẳng d: 3x – 4y – 1 = 0.

Lời giải:

Theo giả thiết ta có phương trình của đường thẳng d: 3x – 4y – 1 = 0 nên d có vectơ pháp tuyến $\overrightarrow{n}$(3; -4) hay vectơ chỉ phương của đường thẳng d $\overrightarrow{u}$(4; 3)

Vì đường thẳng ∆ song song với đường thẳng d nên đường thẳng ∆ nhận $\overrightarrow{u}$(4; 3) làm vectơ chỉ phương.

Vậy phương trình tham số của đường thẳng ∆ đi qua điểm M(-1; 2) và nhận $\overrightarrow{u}$(4; 3) làm vectơ chỉ phương là: $\left\{\begin{array}{l}x=-1+4t\\ y=2+3t\end{array}\right.$.

Luyện tập 5 trang 33 Toán 10 Tập 2: Lập phương trình tham số và phương trình tổng quát của đường thẳng đi qua hai điểm phân biệt A(x1; y1), B(x2; y2) cho trước.

Lời giải:

Ta có: $\overrightarrow{AB}$= (x2 – x1; y2 – y1).

Đường thẳng AB đi qua điểm A(x1; y1) và có vectơ chỉ phương $\overrightarrow{AB}$= (x2 – x1; y2 – y1) do đó phương trình tham số là :

$\left\{\begin{array}{l}x=x_1+(x_2-x_1)t\\ y=y_1+(y_2-y_1)t\end{array}\right.$

Đường thẳng AB có vectơ chỉ phương $\overrightarrow{AB}$= (x2 – x1; y2 – y1) , do đó có vectơ pháp tuyến là: $\overrightarrow{n}$= (y1 – y2; x2 – x1)

Vậy phương trình tổng quát của đường thẳng AB là:

(y1 – y2)(x – x1) + (x2 – x1)(y – y1) = 0

⇔ (y1 – y2)x + (x2 – x1)y – y1x1 + y2x1 – x2y1 + x1y1 = 0

⇔ (y1 – y2)x + (x2 – x1)y + y2x1 –  x2y1 = 0.

Vậy phương trình tham số của đường thẳng AB là $\left\{\begin{array}{l}x=x_1+(x_2-x_1)t\\ y=y_1+(y_2-y_1)t\end{array}\right.$, phương trình tổng quát của đường thẳng AB là (y1 – y2)x + (x2 – x1)y + y2x1 –  x2y1 = 0.

Vận dụng trang 34 Toán 10 Tập 2: Việc quy đổi nhiệt độ giữa đơn vị độ C (Anders Celsius, 1701 – 1744) và đơn vị độ F (Daniel Fahrenheit, 1686 – 1736) được xác định bởi hai mốc sau:

Nước đóng băng ở 0ºC; 32ºF

Nước sôi ở 100ºC; 212ºF

Trong quy đổi đó, nếu aºC tương ứng với bºF thì trên mặt phẳng toạ độ Oxy, điểm M(a; b) thuộc đường thẳng đi qua A(0; 32) và B(100; 212). Hỏi 0ºF, 100ºF tương ứng với bao nhiêu độ C?

Lời giải:

Ta có: $\overrightarrow{AB}$= (100; 180)

Đường thẳng AB đi qua điểm A(0; 32) và có vectơ chỉ phương $\overrightarrow{u}$=$\frac{1}{20}\overrightarrow{AB}$= (5; 9) do đó vectơ pháp tuyến $\overrightarrow{n}$= (-9; 5). Vậy phương trình tổng quát là :

-9(x – 0) + 5(y – 32) = 0

⇔ –9x + 5y – 160 = 0

+ Với 0ºF tương ứng với y = 0 ta có: –9x + 5.0 – 160 = 0 suy ra x ≈ –17, 78

Suy ra 0ºF tương ứng với –17,78ºC.

+ Với 100ºF tương ứng với y = 100 ta có: –9x + 5.100 – 160 = 0 suy ra x ≈ 37,78

Suy ra 0ºF tương ứng với 37,78ºC.

Vậy 0°F tương ứng với  -17,78°C và 100°F tương ứng với  -37,78°C.

B. Bài tập

Bài 7.1 trang 34 Toán 10 Tập 2: Trong mặt phẳng toạ độ, cho $\overrightarrow{n}$= (2; 1) , $\overrightarrow{v}$= (3; 2), A(1; 3), B(-2; 1).

a) Lập phương trình tổng quát của đường thẳng ∆1 đi qua A và có vectơ pháp tuyến $\overrightarrow{n}$.

b) Lập phương trình tham số của đường thẳng ∆2 đi qua B và có vectơ chỉ phương $\overrightarrow{v}$.

c) Lập phương trình tham số của đường thẳng AB.

Lời giải:

a) Phương trình tổng quát của đường thẳng ∆1 đi qua A(1; 3) và có vectơ pháp tuyến $\overrightarrow{n}$= (2; 1) là: 2(x – 1) + 1(y – 3) = 0

⇔ 2x – 2 + y – 3 = 0

⇔ 2x + y – 5 = 0

Vậy phương trình tổng quát của đường thẳng ∆1 là 2x + y – 5 = 0.

b) Phương trình tham số của đường thẳng ∆2 đi qua B(-2; 1) và có vectơ chỉ phương $\overrightarrow{v}$= (3; 2) là: $\left\{\begin{array}{l}x=-2+3t\\ y=1+2t\end{array}\right.$.

Vậy phương trình tham số của đường thẳng ∆2 là $\left\{\begin{array}{l}x=-2+3t\\ y=1+2t\end{array}\right.$.

c) Ta có: $\overrightarrow{BA}$= (3; 2)

Phương trình tham số của đường thẳng AB đi qua B(-2; 1) và có vectơ chỉ phương $\overrightarrow{BA}$= (3; 2) là: $\left\{\begin{array}{l}x=-2+3t\\ y=1+2t\end{array}\right.$.

Vậy phương trình tham số của đường thẳng AB là $\left\{\begin{array}{l}x=-2+3t\\ y=1+2t\end{array}\right.$.

Bài 7.2 trang 34 Toán 10 Tập 2: Lập phương trình tổng quát của các trục toạ độ

Lời giải:

* Phương trình tổng quát của trục Ox đi qua điểm O(0; 0) và nhận vectơ đơn vị $\overrightarrow{j}$(0;1) làm VTPT là: 0.(x – 0) + 1.(y – 0) = 0 hay y = 0 .

* Phương trình tổng quát của trục Oy đi qua điểm O(0; 0) và nhận vectơ đơn vị $\overrightarrow{i}$(1; 0) làm VTPT là: 1.(x – 0) + 0.(y – 0) = 0 hay x = 0.

Bài 7.3 trang 34 Toán 10 Tập 2: Cho hai đường thẳng ∆1: $\left\{\begin{array}{l}x=1+2t\\ y=3+5t\end{array}\right.$ và ∆2: 2x + 3y – 5 = 0.

a) Lập phương trình tổng quát của ∆1.

b) Lập phương trình tham số của ∆2.

Lời giải:

a) Đường thẳng ∆1 có vectơ chỉ phương là $\overrightarrow{u_1}$(2; 5), do đó đường thẳng ∆1 có vectơ pháp tuyến là $\overrightarrow{n_1}$(5; -2).

Lấy A(1; 3) là một điểm thuộc đường thẳng ∆1

Suy ra phương trình tổng quát của ∆1 đi qua điểm A(1; 3) và có vectơ pháp tuyến là $\overrightarrow{n_1}$(5; -2) là: 5(x – 1) – 2(y – 3) = 0 ⇔ 5x – 5 – 2y + 6 = 0 hay 5x – 2y + 1 = 0.

Vậy

b) Đường thẳng ∆2 có vectơ pháp tuyến là $\overrightarrow{n_2}$(2; 3), do đó đường thẳng ∆1 có vectơ chỉ phương là $\overrightarrow{u_2}$(3; -2)

Lấy M(1; 1) thuộc đường thẳng ∆2: 2x + 3y – 5 = 0.

Do đó đường thẳng ∆2 đi qua điểm M(1; 1) nhận vectơ $\overrightarrow{u_2}$(3; -2) là vectơ chỉ phương, phương trình tham số của ∆2 là: $\left\{\begin{array}{l}x=1+3t\\ y=1-2t\end{array}\right.$

Bài 7.4 trang 34 Toán 10 Tập 2: Trong mặt phẳng toạ độ, cho tam giác ABC có A(1; 2); B(3; 0) và C(-2; -1)

a) Lập phương trình đường cao kẻ từ A

b) Lập phương trình đường trung tuyến kẻ từ B

Lời giải:

a) Gọi H là chân đường cao kẻ từ A xuống BC

Ta có : AH ⊥ BC nên đường thẳng AH nhận $\overrightarrow{CB}$= (5; 1) làm vectơ pháp tuyến

Suy ra phương tổng quát của đường thẳng AH đi qua điểm A(1; 2) và nhận $\overrightarrow{CB}$= (5; 1) làm VTPT là:

5(x – 1) + 1(y – 2) = 0

⟺ 5x – 5 + y – 2 = 0 hay 5x + y – 7 = 0.

Vậy phương trình đường cao kẻ từ A là 5x + y – 7 = 0.

b) Gọi M là trung điểm của AC

Ta có, toạ độ của điểm M là: $\left\{\begin{array}{l}{x}_M=\frac{x_A+x_C}{2}\\ y_M=\frac{y_A+y_C}{2}\end{array}\right.$  

                                         $\iff \left\{\begin{array}{l}{x}_M=\frac{1-2}{2}=\frac{-1}{2}\\ y_M=\frac{2-1}{2}=\frac{1}{2}\end{array}\right.$ 

⇒ M $\left(\frac{-1}{2};\frac{1}{2}\right)$

⇒$\overrightarrow{MB}=\left(\frac{7}{2};\frac{-1}{2}\right)$

Lấy $\overrightarrow{u}$= $2\overrightarrow{MB}$= (7 ; -1). Khi đó $\overrightarrow{u}$ là một vectơ chỉ phương của đường thẳng BM.

Đường thẳng BM đi qua điểm B(3; 0) và nhận $\overrightarrow{u}$(7; -1) làm vectơ chỉ phương, phương trình tham số của đường thẳng BM là: $\left\{\begin{array}{l}x=3+7t\\ y=-t\end{array}\right.$.

Vậy phương trình tham số của đường trung tuyến kẻ từ B là: $\left\{\begin{array}{l}x=3+7t\\ y=-t\end{array}\right.$.

Bài 7.5 trang 34 Toán 10 Tập 2: (Phương trình đoạn chắn của đường thẳng)

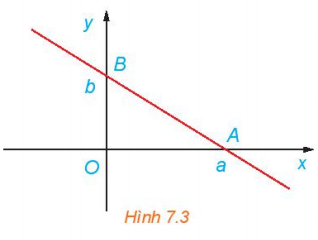
Chứng minh rằng, đường thẳng đi qua hai điểm A(a; 0), B(0; b) với ab ≠ 0 (H7.3) có phương trình là: $\frac{x}{a}+\frac{y}{b}=1$

 

Lời giải:

Ta có: $\overrightarrow{AB}$= (-a; b)

Đường thẳng AB nhận $\overrightarrow{AB}$= (-a; b) làm vectơ chỉ phương, do đó vectơ pháp tuyến là: $\overrightarrow{n}$(b; a)

Vậy phương trình tổng quát của đường thẳng AB đi qua điểm A (a; 0) và có vectơ pháp tuyến $\overrightarrow{n}$(b; a) là: b(x – a) + a(y – 0) = 0

⇔ bx + ay – ab = 0   (1)

Vì ab ≠ 0 nên chia cả 2 vế của (1) cho tích ab ta được: $\frac{x}{a}+\frac{y}{b}-1=0$ hay $\frac{x}{a}+\frac{y}{b}=1$.

Vậy phương trình đường thẳng AB là: $\frac{x}{a}+\frac{y}{b}=1$.

Bài 7.6 trang 34 Toán 10 Tập 2: Theo Google Maps, sân bay Nội  Bài có vĩ độ 21,2º Bắc, kinh độ 105,8º Đông, sân bay Đà Nẵng có vĩ độ 16,1º Bắc, kinh độ 108,2º Đông. Một máy bay bay từ sân bay Nội Bài đến sân bay Đà Nẵng. Tại thời điểm t giờ, tính từ lúc xuất phát, máy bay ở vị trí có vĩ độ xº Bắc , kinh độ yº Đông được tính theo công thức:

$\left\{\begin{array}{l}x=\mathrm{21,2}-\frac{153}{40}t\\ y=\mathrm{105,8}+\frac{9}{5}t\end{array}\right.$

a) Hỏi chuyến bay từ Hà Nội đến Đà Nẵng mất mấy giờ?

b) Tại thời điểm 1 giờ kể từ lúc cất cánh máy bay đã bay qua vĩ tuyến 17 (17º Bắc) chưa?

Lời giải:

a) Tại sân bay Đà Nẵng có vĩ độ 16,1$°$ Bắc, kinh độ 108,2$°$ Đông tương ứng với x = 16,1; y = 108,2

Theo giả thiết ta có: $\left\{\begin{array}{l}\mathrm{16,1}=\mathrm{21,2}-\frac{153}{40}t\\ \mathrm{108,2}=\mathrm{105,8}+\frac{9}{5}t\end{array}\right.$ ⇒ t = $\frac{4}{3}$

Vậy chuyến bay từ Hà Nội đến Đà Nẵng mất $\frac{4}{3}$ giờ.

b) Tại thời điểm 1 giờ tương ứng với t = 1 ta có: $\left\{\begin{array}{l}x=\mathrm{21,2}-\frac{153}{40}.1\\ y=\mathrm{105,8}+\frac{9}{5}.1\end{array}\right.$ ⇒ $\left\{\begin{array}{l}x=\mathrm{17,375}\\ y=\mathrm{107,6}\end{array}\right.$

Tại thời điểm 1 giờ kể từ lúc cất cánh máy bay ở vị trí có vĩ độ 17,375º Bắc , kinh độ 107,6º Đông

Vậy tại thời điểm 1 giờ kể từ lúc cất cánh máy bay đã bay qua vĩ tuyến 17 (17º Bắc).

Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 6

Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Bài 21: Đường tròn trong mặt phẳng tọa độ

Bài 22: Ba đường Conic