Giải SGK Toán 10 (Kết nối tri thức): Bài tập cuối chương 7

Giải bài tập Toán lớp 10 Bài tập cuối chương 7

A. Trắc nghiệm

Bài 7.26 trang 58 Toán 10 Tập 2: Phương trình nào sau đây là phương trình tham số của đường thẳng?

A. 2x – y + 1 = 0;

B. $\left\{\begin{array}{l}x=2t\\ y=t\end{array}\right.$;

C. x2 + y2 = 1;

D. y = 2x + 3.

Lời giải:

Ta thấy 2x – y + 1 = 0; y = 2x + 3 là phương trình tổng quát của đường thẳng. Do đó A, D sai.

Ta thấy x2 + y2 = 1 là phương trình đường tròn. Do đó C sai.

Phương trình $\left\{\begin{array}{l}x=2t\\ y=t\end{array}\right.$ là phương trình tham số của đường thẳng. Do đó B đúng.

Vậy chọn đáp án B.

Bài 7.27 trang 58 Toán 10 Tập 2: Phương trình nào sau đây là phương trình tổng quát của đường thẳng?

A. –x – 2y + 3 = 0;

B. $\left\{\begin{array}{l}x=2+t\\ y=3-t\end{array}\right.$;

C. y2 = 2x;

D. $\frac{x^2}{10}+\frac{y^2}{6}=1$.

Lời giải:

Ta có:

$\left\{\begin{array}{l}x=2+t\\ y=3-t\end{array}\right.$ là phương trình tham số của đường thẳng. Do đó B sai.

 y2 = 2x là phương trình chính tắc của parabol. Do đó C sai.

$\frac{x^2}{10}+\frac{y^2}{6}=1$ là phương trình chính tắc của elip. Do đó D sai.

–x – 2y + 3 = 0 là phương trình tổng quát của đường thẳng. Do đó A đúng.

Vậy chọn đáp án A.

Bài 7.28 trang 58 Toán 10 Tập 2: Phương trình nào sau đây là phương trình đường tròn ?

A. x² – y² = 1;

B. (x – 2)² – (y – 2)² = 1;

C. x² + y² = 2;

D. y² = 8x.

Lời giải:

 x² – y² =  1 có hệ hệ số của y² là – 1 ≠ 1 nên phương trình x² – y² =  1 không là phương trình đường tròn. Do đó A sai.

(x – 2)² – (y – 2)² = 1 không thoả mãn dạng của phương trình đường tròn (x – a)² + (y – b)² = R². Do đó B sai.

y² = 8x là phương trình chính tắc của parabol. Do đó D sai.

x² + y² = 2 là phương trình đường tròn có tâm I(0;0) và R = $\sqrt{2}$. Do đó C đúng.

Vậy chọn đáp án C.

Bài 7.29 trang 58 Toán 10 Tập 2: Phương trình nào sau đây là phương trình chính tắc của đường elip?

A. $\frac{x^2}{9}+\frac{y^2}{9}=1$;

B. $\frac{x^2}{1}+\frac{y^2}{6}=1$;

C. $\frac{x^2}{4}-\frac{y^2}{1}=1$;

D. $\frac{x^2}{2}+\frac{y^2}{1}=1$

Lời giải:

$\frac{x^2}{9}+\frac{y^2}{9}=1$ có a =  b = 3 không thoả mãn điều kiện a > b > 0 nên $\frac{x^2}{9}+\frac{y^2}{9}=1$ không là phương trình chính tắc của đường elip. Do đó A sai

$\frac{x^2}{1}+\frac{y^2}{6}=1$ có a = 1; b = $\sqrt{6}$mà a < b không thoả mãn điều kiện a > b > 0 nên $\frac{x^2}{1}+\frac{y^2}{6}=1$ không là phương trình chính tắc của đường elip. Do đó B sai

$\frac{x^2}{4}-\frac{y^2}{1}=1$là phương trình hypebol. Do đó C sai

$\frac{x^2}{2}+\frac{y^2}{1}=1$ là phương trình elip vì a = $\sqrt{2}$; b = 1 nên a > b > 0. Do đó D đúng.

Vậy chọn đáp án D.

Bài 7.30 trang 58 Toán 10 Tập 2: Phương trình nào sau đây là phương trình chính tắc của đường hypebol?

A. $\frac{x^2}{3}-\frac{y^2}{2}=-1$

B. $\frac{x^2}{1}-\frac{y^2}{6}=1$

C. $\frac{x^2}{6}+\frac{y^2}{1}=1$

D. $\frac{x^2}{2}+\frac{y^2}{1}=-1$

Lời giải:

$\frac{x^2}{3}-\frac{y^2}{2}=-1$ không có dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ nên không là phương trình chính tắc của đường hypebol. Do đó A sai

$\frac{x^2}{6}+\frac{y^2}{1}=1$là phương trình elip. Do đó C sai

$\frac{x^2}{2}+\frac{y^2}{1}=-1$ không có dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ nên không là phương trình chính tắc của đường hypebol. Do đó D sai

Đáp án : B. $\frac{x^2}{1}-\frac{y^2}{6}=1$

Vì a = 1; b = $\sqrt{6}$⇒ c = $\sqrt{1+6}=\sqrt{7}$

 Ta có : 1 < $\sqrt{7}$ hay a <  c nên theo định nghĩa hypebol ta có: $\frac{x^2}{1}-\frac{y^2}{6}=1$ là phương trình chính tắc của đường hypebol.

Vậy chọn đáp án B.

Bài 7.31 trang 58 Toán 10 Tập 2: Phương trình nào sau đây là phương trình chính tắc của đường parabol?

A. x² = 4y

B. x² = -6y

C. y² = 4x

D. y² = -4x

Lời giải:

Phương trình chính tắc của parabol có dạng y² = 2px (p > 0).

Ta thấy chỉ có đáp án C có phương trình dạng trên và thỏa mãn p = 2 > 0 ( thoả mãn điều kiện về phương trình chính tắc của parabol).

Vậy đáp án cần chọn là C.

B. Bài tập

Bài 7.32 trang 58 Toán 10 Tập 2: Trong mặt phẳng toạ độ, cho A(1; −1), B(3; 5); C(−2; 4). Tính diện tích tam giác ABC

Lời giải:

Ta có: $\overrightarrow{CB}$= (5; 1) ⇒ BC = $\sqrt{5^2+1^2}$ = $\sqrt{26}$

Ta lại có $\overrightarrow{CB}$= (5; 1) là vectơ chỉ phương của đường thẳng BC nên vectơ pháp tuyến của BC là $\overrightarrow{n}$(−1; 5).

Đường thẳng BC đi qua điểm B(3; 5) và có vectơ pháp tuyến $\overrightarrow{n}$(−1; 5), có phương trình là:

−1(x – 3) + 5(y − 5) = 0 ⇒ −x + 5y – 22 = 0

d(A; BC) = $\frac{\left|-1+5.(-1)–22\right|}{\sqrt{{(-1)}^2+5^2}}$= $\frac{14\sqrt{26}}{13}$.

Khi đó diện tích tam giác ABC là: S = $\frac{1}{2}$. d(A; BC). BC = $\frac{1}{2}$.$\frac{14\sqrt{26}}{13}$.$\sqrt{26}$ =14 (đvdt).

Vậy diện tích tam giác ABC là 14 đvdt.

Bài 7.33 trang 58 Toán 10 Tập 2: Trong mặt phẳng toạ độ, cho hai điểm A(−1; 0) và B(3; 1)

a) Viết phương trình đường tròn tâm A và đi qua B

b) Viết phương trình tổng quát của đường thẳng AB

c) Viết phương trình đường tròn tâm O và tiếp xúc với đường thẳng AB

Lời giải:

a) Phương trình đường tròn tâm A có dạng : (x + 1)2 + y2 = R2 (với R là bán kính của đường tròn tâm A).

Vì đường tròn đi qua điểm B(3; 1) nên (3 + 1)2 + 12 = R2 ⇒ R2 = 17

Vậy phương trình đường tròn là: (x + 1)2 + y2 = 17

b) Đường thẳng AB có vectơ chỉ phương $\overrightarrow{AB}$= (4; 1) nên vectơ pháp tuyến là $\overrightarrow{n}$(−1; 4).

Vậy phương trình đường thẳng AB là: −1(x + 1) + 4(y – 0) = 0 hay –x + 4y −1 = 0.

c) Vì đường tròn tâm O và tiếp xúc với đường thẳng AB nên

R = d(O; AB) = $\frac{\left|-0+4.0-1\right|}{\sqrt{{(-1)}^2+4^2}}$= $\frac{1}{\sqrt{17}}$

Vậy phương trình đường tròn tâm O và tiếp xúc với đường thẳng AB là:

(x – 0)2 + (y – 0)2 = $\frac{1}{17}$ hay x2 + y2 = $\frac{1}{17}$.

Bài 7.34 trang 58 Toán 10 Tập 2: Cho đường tròn (C) có phương trình x² + y² – 4x + 6y – 12 = 0

a) Tìm toạ độ tâm I và bán kính R của (C).

b) Chứng minh rằng điểm M(5; 1) thuộc (C). Viết phương trình tiếp tuyến d của (C) tại M.

Lời giải:

a) Với phương trình x² + y² – 4x + 6y – 12 = 0 hay x² + y² – 2.2x – 2.( –3) y + (– 12) = 0.

⇒ a = 2; b = –3; c = –12

Khi đó, tâm I(2; –3) và bán kinh R = $\sqrt{a^2+b^2-c}=\sqrt{2^2+{(-3)}^2+12}=5$

b) Thay tọa độ điểm M vào phương trình đường tròn (C) ta được:

52 + 12 – 4.5 + 6.1 – 12 = 0

⇔ 25 + 1 – 20 + 6 – 12 = 0

⇔ 0 = 0 (luôn đúng)

⇒  M(5; 1) ∈ (C).

Ta có: $\overrightarrow{IM}$= (3; 4)

Vì d là phương trình tiếp tuyến của (C) tại M nên IM ⊥ d, do đó đường thẳng d nhận $\overrightarrow{IM}$= (3; 4) làm vectơ pháp tuyến.

Phương trình tiếp tuyến d của (C) tại M(5; 1) có vectơ pháp tuyến $\overrightarrow{IM}$= (3; 4) là:

3(x – 5) + 4(y – 1) = 0 ⇔ 3x + 4y – 19 = 0.

Bài 7.35 trang 59 Toán 10 Tập 2: Cho elip (E) : $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a > b > 0)

a) Tìm các giao điểm A1, A2 của (E) với trục hoành và các giao điểm B1, B2 của (E) với trục tung. Tính A1A2; B1B2

b) Xét một điểm bất kì M(x0; y0) thuộc (E).

Chứng minh rằng: b2  ≤ $x_0^2+y_0^2$ ≤  a2 và b ≤ OM ≤ a

Chú ý: A1A2; B1B2 tương ứng được là trục lớn, trục nhỏ của elip (E) và tương ứng có độ dài là 2a, 2b              

Lời giải:

a) Giao điểm của (E) với trục hoành có y = 0 nên $\frac{x^2}{a^2}+\frac{0^2}{b^2}=1$ ⇒ x2 = a2 ⇒ x = ± a

Do đó, giao điểm của (E) với trục hoành lần lượt là: A1(−a; 0),  A2(a; 0).

⇒ $\overrightarrow{A_1{A}_2}\left(2a;0\right)$ ⇒ A1A2 = $\sqrt{{\left(2a\right)}^2+0^2}$= 2a.

Giao điểm của (E) với trục tung có x = 0 nên $\frac{0^2}{a^2}+\frac{y^2}{b^2}=1$ ⇒ y2  = b2 ⇒ y = ± b

Do đó, giao điểm của (E) với trục tung lần lượt là: B1(0; −b),  B2(0; b).

⇒ $\overrightarrow{B_1{B}_2}\left(0;2b\right)$ ⇒ B1B2 = $\sqrt{0^2+{\left(2b\right)}^2}$= 2b.

Vậy A1(−a; 0),  A2(a; 0), B1(0; −b),  B2(0; b), A1A2 = 2a, B1B2 = 2b.

b) Vì M(x0; y0) thuộc (E) nên $\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1$

Vì a > b > 0 nên $\frac{x_0^2}{a^2}\le \frac{x_0^2}{b^2}$ (Dấu “=” xảy ra khi x0 = 0)

⇔ $\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}\le \frac{x_0^2}{b^2}+\frac{y_0^2}{b^2}$ hay $1\le \frac{x_0^2}{b^2}+\frac{y_0^2}{b^2}=\frac{x_0^2+y_0^2}{b^2}$ 

⇒  b2  ≤ $x_0^2+y_0^2$ (1)

Tương tự ta có: $\frac{y_0^2}{a^2}\le \frac{y_0^2}{b^2}$ (Dấu “=” xảy ra khi y0 = 0)

⇔$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}\ge \frac{x_0^2}{a^2}+\frac{y_0^2}{a^2}$ hay $1\ge \frac{x_0^2}{a^2}+\frac{y_0^2}{a^2}$ ⇒ $x_0^2+y_0^2$ ≤ a2 (2)

Từ (1) và (2) suy ra: b2  ≤ $x_0^2+y_0^2$≤  a2 (đpcm)

Mặt khác ta có: $\overrightarrow{OM}$= (x0; y0) ⟹ OM = $\sqrt{x_0^2+y_0^2}$

Mà b2  ≤ $x_0^2+y_0^2$≤  a2 ⇒  b ≤ $\sqrt{x_0^2+y_0^2}$ ≤  a hay b ≤ OM ≤ a (đpcm).

Bài 7.36 trang 59 Toán 10 Tập 2: Cho hypebol có phương trình : $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

a) Tìm các giao điểm A1, A2 của hypebol với trục hoành (hoành độ của A1 nhỏ hơn của A2).

b) Chứng minh rằng, nếu điểm M(x; y) thuộc nhánh nằm bên trái trục tung của hypebol thì x ≤ –a, nếu điểm M(x; y) thuộc nhánh nằm bên phải trục tung của hypebol thì x ≥ a.

c) Tìm các điểm M1, M2 tương ứng thuộc các nhánh bên trái, bên phải trục tung của hyperbol để M1M2 nhỏ nhất.

Lời giải:

a) Giao điểm của (H) với trục hoành có y = 0 nên $\frac{x^2}{a^2}-\frac{0^2}{b^2}=1$ ⇒ x2  = a2 ⇒ x = ± a;

Hơn nữa hoành độ A1 nhỏ hơn hoành độ A2 nên ta có: A1(−a; 0),  A2(a; 0).

Vậy tọa độ giao điểm của hypebol với trục hoành lần lượt là A1(−a; 0),  A2(a; 0).

b) Ta có: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ 

⇔ $\frac{x^2}{a^2}=1+\frac{y^2}{b^2}$ 

Mà $\frac{y^2}{b^2}$≥ 0 nên $\frac{x^2}{a^2}\ge 1$ hay x2 ≥ a2  

⇔ |x| ≥ |a|

⇔ x ≥ a hoặc x ≤ – a .

Vậy điểm M(x; y) thuộc nhánh nằm bên trái trục tung của hypebol thì x ≤ 0 nên x ≤ –a, nếu điểm M(x; y) thuộc nhánh nằm bên phải trục tung của hypebol thì x ≥ 0 nên x ≥ a.

b) Gọi toạ độ điểm M1(x1;y1),  M2(x2;y2), tương ứng thuộc các nhánh bên trái, bên phải trục tung của hypebol. Khi đó x1 ≤ – a và x2 ≥ a.

Ta có

$\overrightarrow{M_1{M}_2}\left(x_2-x_1;y_2-y_1\right)$ ⇒ M1M2 = $\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$;

 A1A2 = $\sqrt{{(a-(-a\left)\right)}^2+{(0-0)}^2}$ = 2a.

Vì x1 < 0 và x2 > 0 nên x2 – x1 = $\left|x_2\right|$+$\left|x_1\right|$ (1)

Mặt khác ta có: x1 ≤ –a  và x2  ≥  a ⇒ $\left|x_2\right|$  ≥  a và $\left|x_1\right|$ ≥  a

                                                        ⇒ $\left|x_2\right|$+$\left|x_1\right|$ ≥  a + a = 2a  (2)

Từ (1) và (2) ta có: x2 – x1 ≥  2a ⇒ (x2 – x1)2 ≥  (2a)2  

Ta lại có: (y2 – y1)2  ≥ 0

⇒  (x2 – x1)2 + (y2 – y1)2  ≥  (2a)2  + 0 = (2a)2 

⇒ $\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$ ≥  2a  hay M1M2 ≥ A1A2

Vậy M1M2 nhỏ nhất khi M1M2 = A1A2

Dấu “=” xảy ra khi diểm M1 ≡ A1(-a; 0) và  M2  ≡ A2(a; 0).

Bài 7.37 trang 59 Toán 10 Tập 2: Một cột trụ hình hyperbol (H.7.36), có chiều cao 6m, chỗ nhỏ nhất ở chính giữa và rộng 0,8m, đỉnh cột và đáy cột đều rộng 1m. Tính độ rộng của cột ở độ cao 5m (Tính theo đơn vị mét và làm tròn tới hai chữ số sau dấu phẩy).

 

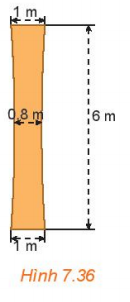
Lời giải:

Chọn hệ trục tọa độ Oxy có gốc O là chỗ nhỏ nhất ở chính giữa, như hình vẽ sau:

 

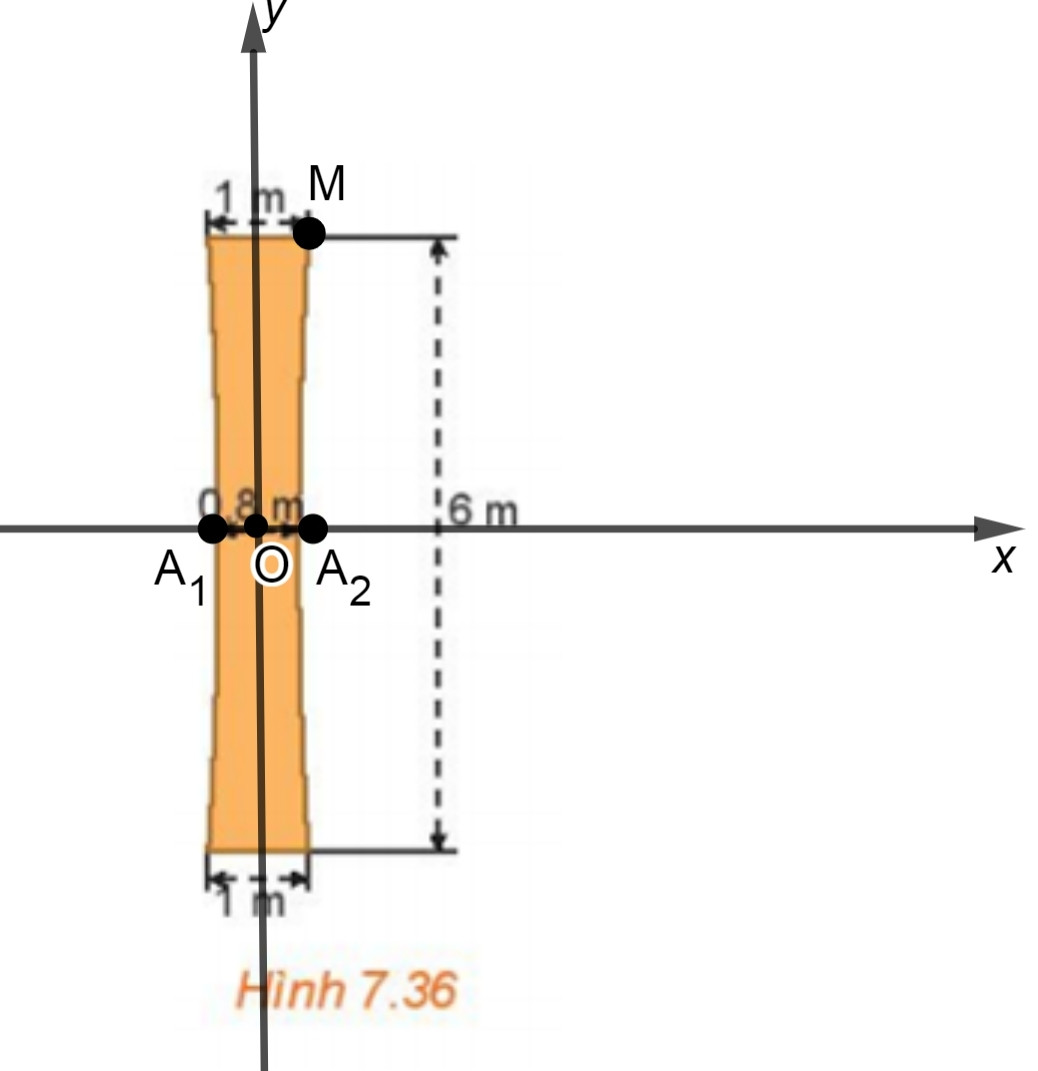
Gọi A1, A2 lần lượt là giao điểm của hypebol với trục hoành mà O là trung điểm của A1A2 nên A1(−0,4 ; 0),  A2(0,4 ; 0) hay a = 0,4.

Gọi phương trình hypebol của hình trụ có dạng : $\frac{x^2}{{\mathrm{0,4}}^2}-\frac{y^2}{b^2}=1$.

Gọi M là một điểm trên đỉnh cột nằm ở nhánh bên phải của trục tung hypebol. Ta có toạ độ điểm M(0,5; 3).

Vì điểm M(0,5; 3) thuộc (H) nên $\frac{{\mathrm{0,5}}^2}{{\mathrm{0,4}}^2}-\frac{3^2}{b^2}=1$

⇔$\frac{25}{16}-\frac{3^2}{b^2}=1$

⇔$\frac{3^2}{b^2}=\frac{25}{16}-1=\frac{9}{16}$ 

⇒ b2 = 16

Do đó phương trình hypebol của hình trụ đó là: $\frac{x^2}{{\mathrm{0,4}}^2}-\frac{y^2}{16}=1$

Tại vị trí 5m thì điểm đó cách trục hoành một khoảng bằng 2m nên ta có y = 2.

Thay y = 2 vào phương trình hypebol ta được:

$\frac{x^2}{{\mathrm{0,4}}^2}-\frac{2^2}{16}=1$

⇔$\frac{x^2}{{\mathrm{0,4}}^2}=\frac{20}{16}$

⇒ x2 = 0,2 ⇒x =$\sqrt{\mathrm{0,2}}$≈±0,45

Vậy độ rộng tại vị trí có độ cao 5m xấp xỉ là: 0,45.2 = 0,9 m.

Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:

Bài 22: Ba đường Conic

Bài 23: Quy tắc đếm

Bài 24: Hoán vị, chỉnh hợp và tổ hợp

Bài 25: Nhị thức Newton