Lý thuyết Toán lớp 10 Bài 3: Phương trình đường thẳng
A. Lý thuyết Phương trình đường thẳng
I. Phương trình tham số của đường thẳng
1. Vectơ chỉ phương của đường thẳng
Vectơ được gọi là vectơ chỉ phương của đường thẳng ∆ nếu ≠ và giá của song song hoặc trùng với ∆.
Nhận xét:
– Nếu là một vectơ chỉ phương của ∆ thì k (k ≠ 0) cũng là một vectơ chỉ phương của ∆.
– Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vectơ chỉ phương của đường thẳng đó.
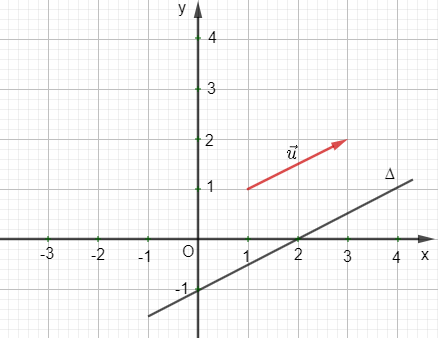
Ví dụ: Đường thẳng ∆ đi qua điểm (2 ; 0) và (0 ; –1) có vectơ chỉ phương như hình vẽ sau:
2. Phương trình tham số của đường thẳng
Hệ (a2 + b2 > 0 và t là tham số) được gọi là phương trình tham số của đường thẳng ∆ đi qua M0(x0 ; y0) và nhận = (a ; b) làm vectơ chỉ phương.
Nhận xét: Cho đường thẳng ∆ có phương trình tham số là: (a2 + b2 > 0 và t là tham số).
+ Với mỗi giá trị cụ thể của t, ta xác định được một điểm trên đường thẳng ∆. Ngược lại, với mỗi điểm trên đường thẳng ∆, ta xác định được một giá trị cụ thể của t.
+ Vectơ = (a ; b) là một vectơ chỉ phương của ∆.
Ví dụ:
a) Viết phương trình tham số của đường thẳng ∆ đi qua điểm A(1; 2) và có vectơ chỉ phương = (–1 ; 3).
b) Cho đường thẳng ∆ có phương trình tham số là . Chỉ ra tọa độ một vectơ chỉ phương của ∆ và một điểm thuộc đường thẳng ∆.
Hướng dẫn giải
a) Phương trình đường thẳng ∆ đi qua điểm A(1; 2) và có vectơ chỉ phương = (–1 ; 3) nên có phương trình tham số là .
Vậy phương trình tham số của đường thẳng ∆ là .
b) Đường thẳng ∆ có phương trình tham số là .
Khi đó ∆ có một vectơ chỉ phương là (2 ; –1) và điểm (4 ; –3) thuộc ∆.
Vậy ∆ có một vectơ chỉ phương là (2 ; –1) và điểm (4 ; –3) thuộc ∆.
II. Phương trình tổng quát của đường thẳng
1. Vectơ pháp tuyến của đường thẳng
Vectơ được gọi là vectơ pháp tuyến của đường thẳng ∆ nếu ≠ và giá của vectơ vuông góc với ∆.
Nhận xét:
– Nếu là một vectơ pháp tuyến của ∆ thì k (k ≠ 0) cũng là một vectơ pháp tuyến của ∆.
– Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vectơ pháp tuyến của đường thẳng đó.
– Nếu một đường thẳng ∆ có vectơ chỉ phương là = (a ; b) thì vectơ = (–b ; a) là một vectơ pháp tuyến của ∆.
2. Phương trình tổng quát của đường thẳng
Phương trình ax + by + c = 0 (a và b không đồng thời bằng 0) được gọi là phương trình tổng quát của đường thẳng.
Nhận xét:
– Đường thẳng ∆ đi qua điểm M0 (x0 ; y0) và nhận = (a ; b) làm vectơ pháp tuyến có phương trình là: a(x – x0) + b(y – y0) = 0 ⇔ ax + by + (–ax0 – by0) = 0.
– Mỗi phương trình ax + by + c = 0 (a và b không đồng thời bằng 0) đều xác định một đường thẳng ∆ trong mặt phẳng tọa độ nhận một vectơ pháp tuyến là = (a ; b).
Ví dụ: Viết phương trình tổng quát của đường thẳng d đi qua điểm A(1; –2) và có vectơ pháp tuyến = (–2 ; –3).
Hướng dẫn giải
Theo giả thiết, phương trình của đường thẳng d là : –2(x – 1) + (–3).(y + 2) = 0.
Từ đó, ta nhận được phương trình tổng quát của đường thẳng d là –2x – 3y – 4 = 0.
Vậy phương trình tổng quát của d là –2x – 3y – 4 = 0.
3. Những dạng đặc biệt của phương trình tổng quát
Cho đường thẳng ∆ có phương trình tổng quát ax + by + c = 0 (a hoặc b khác 0).
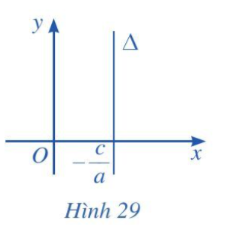
a) Nếu b = 0 và a ≠ 0 thì phương trình đường thẳng ∆ trở thành ax + c = 0. Khi đó đường thẳng ∆ song song hoặc trùng với trục Oy và cắt trục Ox tại điểm .
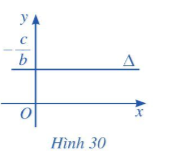
b) Nếu b ≠ 0 và a = 0 thì phương trình đường thẳng ∆ trở thành by + c = 0. Khi đó đường thẳng ∆ song song hoặc trùng với trục Ox và cắt trục Oy tại điểm (Hình 30).
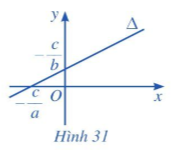
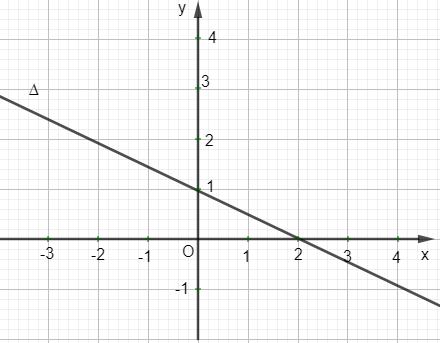
c) Nếu b ≠ 0 và a ≠ 0 thì phương trình đường thẳng ∆ có thể viết thành
y = x – .
Khi đó, đường thẳng ∆ là đồ thị hàm số bậc nhất y = x – với hệ số góc là k = (Hình 31).
Nhận xét:
– Đường thẳng ∆ có phương trình tổng quát ax + by + c = 0 (a hoặc b khác 0) là đồ thị của hàm số bậc nhất khi và chỉ khi a ≠ 0 và b ≠ 0.
– Phương trình trục hoành là y = 0, phương trình trục tung là x = 0.
Ví dụ:
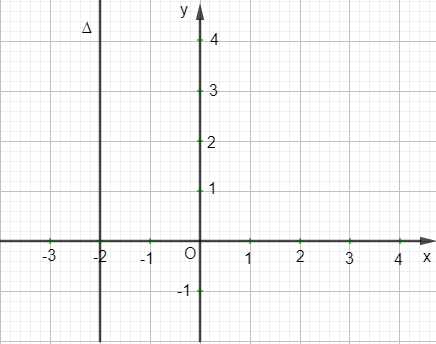
a) Cho phương trình đường thẳng ∆ là 2x + 4 = 0. Khi đó đường thẳng ∆ song song với trục Oy và cắt trục Ox tại điểm (–2 ; 0)
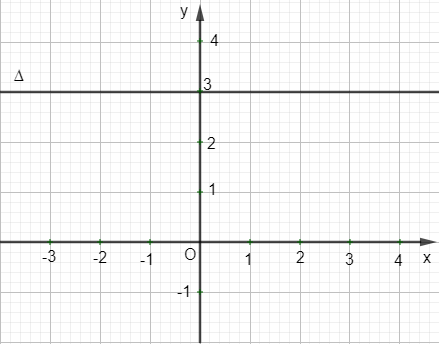
b) Cho phương trình đường thẳng ∆ là 3x – 9 = 0. Khi đó đường thẳng ∆ song song với trục Ox và cắt trục Oy tại điểm (0 ; 3)
c) Cho phương trình đường thẳng ∆ là x + 2y – 2 = 0. Khi đó, đường thẳng ∆ là đồ thị của hàm số bậc nhất y = x + 1 với hệ số góc k =
III. Lập phương trình đường thẳng
1. Lập phương trình đường thẳng đi qua một điểm và biết vectơ pháp tuyến
Phương trình đường thẳng ∆ đi qua điểm M0(x0 ; y0) và nhận = (a ; b) ( ≠ ) làm vectơ pháp tuyến là a(x – x0) + b(y – y0) = 0.
Ví dụ: Lập phương trình của đường thẳng ∆ đi qua điểm M(2; –2) và có vectơ pháp tuyến = (2 ; 3).
Hướng dẫn giải
Theo giả thiết, phương trình của đường thẳng ∆ là: 2(x – 2) + 3.(y + 2) = 0.
Từ đó, ta nhận được phương trình của đường thẳng ∆ là 2x + 3y + 2 = 0.
Vậy phương trình của ∆ là 2x + 3y + 2 = 0.
2. Lập phương trình đường thẳng đi qua một điểm và biết vectơ chỉ phương
Phương trình tham số của đường thẳng ∆ đi qua điểm M0(x0 ; y0) và nhận = (a ; b) (≠ ) làm vectơ chỉ phương là (t là tham số).
Nếu a ≠ 0 và b ≠ 0 thì ta còn có thể viết phương trình của đường thẳng ∆ ở dạng: .
Ví dụ: Viết phương trình tham số của đường thẳng ∆ đi qua điểm M(–1; 2) và có vectơ chỉ phương = (1 ; –3).
Hướng dẫn giải
Cách 1: Phương trình tham số của đường thẳng ∆ đi qua điểm M(–1; 2) và có vectơ chỉ phương = (1 ; –3) là .
Vậy phương trình tham số của đường thẳng ∆ là .
Cách 2: Phương trình đường thẳng ∆ đi qua điểm M(–1; 2) và có vectơ chỉ phương = (1 ; –3) nên có phương trình là ⇔ –3x – y – 1= 0.
Vậy phương trình của đường thẳng ∆ là –3x – y – 1= 0.
3. Lập phương trình đi qua hai điểm
Đường thẳng ∆ đi qua hai điểm A(x0 ; y0), B(x1 ; y1) nên nhận vectơ = (x1 – x0 ; y1 – y0) làm vectơ chỉ phương. Do đó, phương trình tham số của đường thẳng ∆ là: (t là tham số).
Nếu x1 – x0 ≠ 0 và y1 – y0 ≠ 0 thì ta còn có thể viết phương trình của đường thẳng ∆ ở dạng: .
Ví dụ: Lập phương trình ∆ đi qua hai điểm A(2 ; 2) và B(–1 ; 3).
Hướng dẫn giải
Phương trình ∆ đi qua hai điểm A(2 ; 2) và B(–1 ; 3) là
⇔ ⇔ x + 3y – 8 = 0.
Vậy phương trình đường thẳng ∆ đi qua hai điểm A(2 ; 2) và B(–1 ; 3) là x + 3y – 8 = 0.
B. Bài tập tự luyện
B.1 Bài tập tự luận
Bài 1. Cho đường thẳng ∆ có phương trình tổng quát là –x + 7y – 5 = 0.
a) Lập phương trình tham số của đường thẳng ∆.
b) Tìm tọa độ giao điểm của đường thẳng ∆ lần lượt với các trục Ox, Oy.
Hướng dẫn giải
a) Đường thẳng ∆ có phương trình tổng quát là –x + 7y – 5 = 0 nên có vectơ pháp tuyến = (–1 ; 7).
Suy ra đường thẳng ∆ có vectơ chỉ phương là = (7 ; 1).
Ta thấy điểm A(–5 ; 0) thuộc ∆.
Khi đó, phương trình tham số của đường thẳng ∆ đi qua điểm A(–5 ; 0) có vectơ chỉ phương = (7 ; 1) là:
Vậy phương trình tham số của đường thẳng ∆ là .
b) Tọa độ giao điểm của ∆ với trục Ox là nghiệm của hệ:
Giải hệ ta được
Suy ra tọa độ giao điểm của ∆ với trục Ox là (–5 ; 0).
Tọa độ giao điểm của ∆ với trục Oy là nghiệm của hệ:
Giải hệ ta được
Suy ra tọa độ giao điểm của ∆ với trục Oy là
Vậy tọa độ giao điểm của ∆ với trục Ox, Oy lần lượt là (–5 ; 0) và .
Bài 2. Cho tam giác ABC có A(0; 4), B(–3; 2), C(1; 6).
a) Lập phương trình của đường thẳng BC.
b) Lập phương trình đường trung trực của đoạn thẳng AB.
c) Lập phương trình đường trung tuyến AM của tam giác ABC.
Hướng dẫn giải
a) Phương trình đường thẳng BC đi qua hai điểm B(–3; 2), C(1; 6) là
⇔ ⇔ x – y + 5 = 0.
Vậy phương trình đường thẳng BC là x – y + 5 = 0.
b) Gọi I(xI ; yI) là trung điểm của AB.
Khi đó ; .
Suy ra .
Đường trung trực của AB đi qua điểm I và nhận vectơ = (–3 ; –2) làm vectơ pháp tuyến.
Khi đó đường trung trực của AB có phương trình là:
–3(x – ) – 2(y – 3) = 0 ⇔ –3x – 2y + = 0.
Vậy phương trình đường trung trực của AB là –3x – 2y + = 0.
c) Gọi M(xM ; yM) là trung điểm của đoạn thẳng BC.
Khi đó ; .
Suy ra M(–1 ; 4).
Đường trung tuyến AM đi qua hai điểm A và có vectơ chỉ phương = (–1 ; 0) có phương trình là:
Vậy đường trung tuyến AM có phương trình là .
Bài 3. Viết phương trình đường thẳng d biết:
a) Đường thẳng d đi qua điểm M(4; 3) và có vectơ pháp tuyến là = (3; –4).
b) Đường thẳng d đi qua điểm M(0 ; –2) và có vectơ chỉ phương là = (1; 1).
c) Đường thẳng d đi qua hai điểm A(–1 ; 3) và B(2 ; –6).
Hướng dẫn giải
a) Phương trình đường thẳng d đi qua điểm M(4; 3) và có vectơ pháp tuyến là = (3; –4) là: 3(x – 4) – 4.(y – 3) = 0 ⇔ 3x – 4y = 0.
Vậy phương trình của ∆ là 3x – 4y = 0.
b) Phương trình tham số của đường thẳng d đi qua điểm M(0 ; –2) và có vectơ chỉ phương là = (1; 1) là ⇔
Vậy phương trình tham số của đường thẳng d đi qua điểm M(0 ; –2) và có vectơ chỉ phương là = (1; 1) là .
c) Phương trình d đi qua hai điểm A(–1 ; 3) và B(2 ; –6) là
⇔ ⇔ 3x + y = 0.
Vậy phương trình đường thẳng ∆ đi qua hai điểm A(–1 ; 3) và B(2 ; –6) là 3x + y = 0.
B.2 Bài tập trắc nghiệm
Câu 1. Đường thẳng d đi qua điểm M(1; – 2) và có vectơ chỉ phương có phương trình tham số là:
A. ;
B. ;
C. ;
D. .
Hướng dẫn giải
Đáp án đúng là: B
Ta có:
Phương trình tham số
Câu 2. Phương trình tổng quát của đường thẳng đi qua hai điểm A(3 ; – 1) và B(1 ; 5) là:
A. – 2x + 3y + 6 = 0 ;
B. 3x – 2y + 10 = 0;
C. 3x – 2y + 6 = 0 ;
D. 3x + y – 8 = 0.
Hướng dẫn giải
Đáp án đúng là: D
Vectơ chỉ phương của AB là
là vectơ pháp tuyến của đường thẳng qua hai điểm A, B.
Mặt khác A(3; – 1) ∈ AB, suy ra phương trình tổng quát của đường thẳng AB là:
3(x – 3) + 1(y + 1) = 0 hay 3x + y – 8 = 0.
Câu 3. Phương trình đường thẳng cắt hai trục tọa độ tại A(– 2 ; 0) và B(0 ; 4) là:
A. 2x – 3y + 2 = 0;
B. 4x – 2y + 8 = 0;
C. 3x – 3y – 6 = 0;
D. 2x – 3y – 5 = 0.
Hướng dẫn giải
Đáp án đúng là: B
Ta có:
Do đó, phương trình đường thẳng: 4x – 2y + 8 = 0 hay 2x – y + 4 = 0.
Xem thêm các bài tóm tắt lý thuyết Toán lớp 10 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 4: Xác suất của biến cố trong một số trò chơi đơn giản
Lý thuyết Bài 5: Xác suất của biến cố
Lý thuyết Bài 1: Tọa độ của vectơ
Lý thuyết Bài 2: Biểu thức tọa độ của các phép toán vectơ
Lý thuyết Bài 3: Phương trình đường thẳng