Lý thuyết Tích của một số với một vectơ (Cánh diều 2023) hay, chi tiết | Toán lớp 10

Lý thuyết Toán lớp 10 Bài 5: Tích của một số với một vectơ

Video giải Toán 10 Bài 5: Tích của một số với một vectơ – Cánh diều

A. Lý thuyết Tích của một số với một vectơ

1. Định nghĩa

Cho một số k ≠ 0 và vectơ $\overrightarrow{\mathrm{a}}$ ≠ $\overrightarrow{0}$. Tích của một số k với vectơ $\overrightarrow{\mathrm{a}}$ là một vectơ, kí hiệu là k$\overrightarrow{\mathrm{a}}$, được xác định như sau:

+ cùng hướng với $\overrightarrow{\mathrm{a}}$ nếu k > 0, ngược hướng với $\overrightarrow{\mathrm{a}}$ nếu k < 0;

+ có độ dài bằng $\left|\mathrm{k}\right|$.$\left|\overrightarrow{\mathrm{a}}\right|$

Quy ước: 0$\overrightarrow{\mathrm{a}}$ = $\overrightarrow{0}$, k$\overrightarrow{0}$ = $\overrightarrow{0}$

Phép lấy tích của một số với một vectơ gọi là phép nhân một số với một vectơ.

Ví dụ: Cho G là trọng tâm của tam giác ABC, D và E lần lượt là trung điểm của BC và AC. Tìm mối quan hệ của $\overrightarrow{\mathrm{GA}}$ và $\overrightarrow{\mathrm{GD}}$; mối quan hệ của $\overrightarrow{\mathrm{AD}}$ và $\overrightarrow{\mathrm{GD}}$ 

Hướng dẫn giải

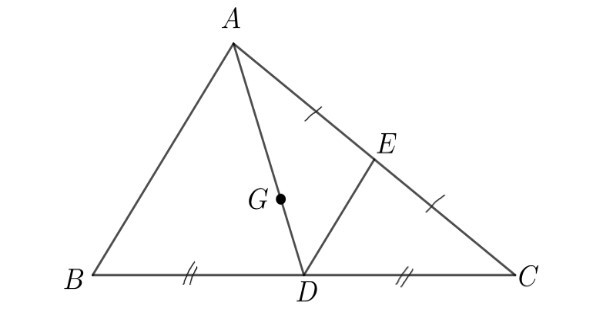
Khi đó ta có:

– Vì G là trọng tâm của tam giác ABC nên GA = 2GD.

Mà G nằm giữa A và D nên $\overrightarrow{\mathrm{GA}}$ và $\overrightarrow{\mathrm{GD}}$ là hai vectơ ngược hướng.

⇒ $\overrightarrow{\mathrm{GA}}$ = (–2)$\overrightarrow{\mathrm{GD}}$.

– Ta có: AD = 3GD.

Mà $\overrightarrow{\mathrm{GD}}$ và $\overrightarrow{\mathrm{AD}}$ là hai vectơ cùng hướng.

⇒ $\overrightarrow{\mathrm{AD}}$= 3$\overrightarrow{\mathrm{GD}}$.

Ví dụ: Cho vectơ $\overrightarrow{\mathrm{a}}$ có $\left|\overrightarrow{\mathrm{a}}\right|$= 4. Tìm số thực x sao cho vectơ x$\overrightarrow{\mathrm{a}}$ có độ dài bằng 1 và cùng hướng với $\overrightarrow{\mathrm{a}}$.

Hướng dẫn giải:

Ta có: $\left|\mathrm{x}\overrightarrow{\mathrm{a}}\right|$ = 1 ⇔ $\left|\mathrm{x}\right|.\left|\overrightarrow{\mathrm{a}}\right|$ = 1 ⇔ $\left|\mathrm{x}\right|.4$= 1

⇔ $\left|\mathrm{x}\right|$ = $\frac{1}{4}$

Lại có vectơ x$\overrightarrow{\mathrm{a}}$ cùng hướng với vectơ $\overrightarrow{\mathrm{a}}$ nên x > 0

Suy ra x = $\frac{1}{4}$.

Vậy x = $\frac{1}{4}$ là giá trị cần tìm.

2. Tính chất

Với hai vectơ bất kì $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$ và hai số thực h, k, ta có:

+) k($\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$) = k$\overrightarrow{\mathrm{a}}$ + k$\overrightarrow{\mathrm{b}}$; k($\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$) = k$\overrightarrow{\mathrm{a}}$ – k$\overrightarrow{\mathrm{b}}$;

+) (h + k)$\overrightarrow{\mathrm{a}}$ = h$\overrightarrow{\mathrm{a}}$ + k$\overrightarrow{\mathrm{a}}$;

+) h(k$\overrightarrow{\mathrm{a}}$) = (hk)$\overrightarrow{\mathrm{a}}$;

+) 1$\overrightarrow{\mathrm{a}}$ = $\overrightarrow{\mathrm{a}}$; (–1)$\overrightarrow{\mathrm{a}}$ = –$\overrightarrow{\mathrm{a}}$.

Nhận xét: k$\overrightarrow{\mathrm{a}}$ = $\overrightarrow{0}$ khi và chỉ khi k = 0 hoặc $\overrightarrow{\mathrm{a}}$ = $\overrightarrow{0}$.

Ví dụ: Tính:

a) 5$\overrightarrow{\mathrm{BC}}$ + 5$\overrightarrow{\mathrm{CA}}$;

b) 4$\overrightarrow{\mathrm{AB}}$ + 6$\overrightarrow{\mathrm{AB}}$;

c) 4(2$\overrightarrow{\mathrm{AB}}$) + 2$\overrightarrow{\mathrm{BC}}$ – 3$\overrightarrow{\mathrm{AB}}$.

Hướng dẫn giải:

3. Một số ứng dụng

3.1. Trung điểm của đoạn thẳng

Nếu I là trung điểm của đoạn thẳng AB thì $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}=2\overrightarrow{\mathrm{MI}}$ với điểm M bất kì.

Chứng minh:

Vì I là trung điểm của đoạn thẳng AB nên $\overrightarrow{\mathrm{IA}}+\overrightarrow{\mathrm{IB}}$ = $\overrightarrow{0}$

Suy ra:

$\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}$ = $\left(\overrightarrow{\mathrm{MI}}+\overrightarrow{\mathrm{IA}}\right)+\left(\overrightarrow{\mathrm{MI}}+\overrightarrow{\mathrm{IB}}\right)$ 

= $\overrightarrow{\mathrm{MI}}+\overrightarrow{\mathrm{MI}}+\overrightarrow{\mathrm{IA}}+\overrightarrow{\mathrm{IB}}$ = $2\overrightarrow{\mathrm{MI}}+\overrightarrow{\mathrm{IA}}+\overrightarrow{\mathrm{IB}}$

= $2\overrightarrow{\mathrm{MI}}+\overrightarrow{0}$ = $2\overrightarrow{\mathrm{MI}}$.

⇒ $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}$ = $2\overrightarrow{\mathrm{MI}}$ (đpcm).

Ví dụ: Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AC, BD. Chứng minh $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MC}}+\overrightarrow{\mathrm{MD}}=2\overrightarrow{\mathrm{MN}}$.

Hướng dẫn giải:

Vì M, N lần lượt là trung điểm của AC, BD nên ta có:

$\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MC}}=\overrightarrow{0}$

$\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MD}}=2\overrightarrow{\mathrm{MN}}$

⇒ $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MC}}+\overrightarrow{\mathrm{MD}}$ = $\left(\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MC}}\right)+\left(\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MD}}\right)$ = $\overrightarrow{0}+2\overrightarrow{\mathrm{MN}}$ = $2\overrightarrow{\mathrm{MN}}$.

⇒ $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MC}}+\overrightarrow{\mathrm{MD}}=2\overrightarrow{\mathrm{MN}}$ (đpcm).

3.2. Trọng tâm của tam giác

Nếu G là trọng tâm của tam giác ABC thì $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MC}}=3\overrightarrow{\mathrm{MG}}$ với điểm M bất kì.

Ví dụ: Gọi G và G’ lần lượt là trọng tâm tam giác ABC và A’B’C’. Chứng minh rằng: $\overrightarrow{\text{AA’}}+\overrightarrow{\mathrm{BB}‘}+\overrightarrow{\mathrm{CC}‘}=3\overrightarrow{\mathrm{GG}‘}$.

Hướng dẫn giải:

Vì G và G’ lần lượt là trọng tâm tam giác ABC và A’B’C’ nên:

$\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}=\overrightarrow{0}$ và $\overrightarrow{\mathrm{GA}‘}+\overrightarrow{\mathrm{GB}‘}+\overrightarrow{\mathrm{GC}‘}=\overrightarrow{0}$

Theo quy tắc cộng vectơ ta có:

$\overrightarrow{\text{AA}‘}=\overrightarrow{\mathrm{AG}}+\overrightarrow{\mathrm{GG}‘}+\overrightarrow{\mathrm{G}‘\mathrm{A}‘}$ (1)

$\overrightarrow{\mathrm{BB}‘}=\overrightarrow{\mathrm{BG}}+\overrightarrow{\mathrm{GG}‘}+\overrightarrow{\mathrm{G}‘\mathrm{B}‘}$ (2)

$\overrightarrow{\mathrm{CC}‘}=\overrightarrow{\mathrm{CG}}+\overrightarrow{\mathrm{GG}‘}+\overrightarrow{\mathrm{G}‘\mathrm{C}‘}$ (3)

Cộng vế với vế của (1), (2) và (3) ta có:

$\overrightarrow{\text{AA’}}+\overrightarrow{\mathrm{BB}‘}+\overrightarrow{\mathrm{CC}‘}$ = $3\overrightarrow{\mathrm{GG}‘}+\left(\overrightarrow{\mathrm{AG}}+\overrightarrow{\mathrm{BG}}+\overrightarrow{\mathrm{CG}}\right)+\left(\overrightarrow{\mathrm{GA}‘}+\overrightarrow{\mathrm{GB}‘}+\overrightarrow{\mathrm{GC}‘}\right)$

= $3\overrightarrow{\mathrm{GG}‘}+\left(-\overrightarrow{\mathrm{GA}}-\overrightarrow{\mathrm{GB}}-\overrightarrow{\mathrm{GC}}\right)+\left(\overrightarrow{\mathrm{GA}‘}+\overrightarrow{\mathrm{GB}‘}+\overrightarrow{\mathrm{GC}‘}\right)$

= $3\overrightarrow{\mathrm{GG}‘}-\left(\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}\right)+\left(\overrightarrow{\mathrm{GA}‘}+\overrightarrow{\mathrm{GB}‘}+\overrightarrow{\mathrm{GC}‘}\right)$

= $3\overrightarrow{\mathrm{GG}‘}+\overrightarrow{0}+\overrightarrow{0}$ = $3\overrightarrow{\mathrm{GG}‘}$

⇒ $\overrightarrow{\text{AA’}}+\overrightarrow{\mathrm{BB}‘}+\overrightarrow{\mathrm{CC}‘}=3\overrightarrow{\mathrm{GG}‘}$ (đpcm).

3.3. Điều kiện để hai vectơ cùng phương. Điều kiện để ba điểm thẳng hàng

– Điều kiện cần và đủ để hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ ($\overrightarrow{\mathrm{b}}$ ≠ 0) cùng phương là có một số thực k để $\overrightarrow{\mathrm{a}}$ = k$\overrightarrow{\mathrm{b}}$.

– Điều kiện cần và đủ để ba điểm phân biệt A, B, C thẳng hàng là có số thực k để $\overrightarrow{\mathrm{AB}}=\mathrm{k}\overrightarrow{\mathrm{AC}}$.

Nhận xét: Trong mặt phẳng, cho hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ không cùng phương. Với mỗi vectơ $\overrightarrow{\mathrm{c}}$ có duy nhất cặp số (x; y) thoả mãn $\overrightarrow{\mathrm{c}}=\mathrm{x}\overrightarrow{\mathrm{a}}+\mathrm{y}\overrightarrow{\mathrm{b}}$.

Ví dụ: Cho tam giác ABC. Đặt $\overrightarrow{\mathrm{a}}=\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{AC}}$. Dựng các điểm M, N sao cho $\overrightarrow{\mathrm{AM}}=\frac{1}{3}\overrightarrow{\mathrm{AB}}$; $\overrightarrow{\mathrm{CN}}=2\overrightarrow{\mathrm{BC}}$.

a) Phân tích $\overrightarrow{\mathrm{CM}}$, $\overrightarrow{\mathrm{AN}}$ theo các vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$.

b) Gọi I là điểm thỏa mãn: $\overrightarrow{\mathrm{MI}}=\overrightarrow{\mathrm{CM}}$. Chứng minh I, A, N thẳng hàng.

Hướng dẫn giải:

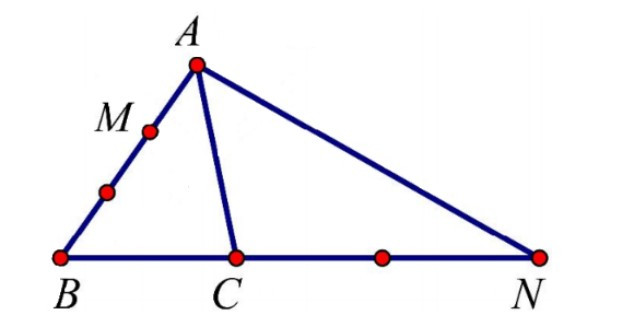
a) Ta có:

+) $\overrightarrow{\mathrm{CM}}$ = $\overrightarrow{\mathrm{CA}}+\overrightarrow{\mathrm{AM}}$ = $-\overrightarrow{\mathrm{AC}}+\frac{1}{3}\overrightarrow{\mathrm{AB}}$ = $\frac{1}{3}$$\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$.

+) Vì $\overrightarrow{\mathrm{CN}}=2\overrightarrow{\mathrm{BC}}$ ⇒ CN = 2BC ⇒ BC = $\frac{1}{3}$BN ⇒ BN = 3BC.

⇒ $\overrightarrow{\mathrm{BN}}=3\overrightarrow{\mathrm{BC}}$.

⇒ $\overrightarrow{\mathrm{AN}}$ = $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BN}}$ = $\overrightarrow{\mathrm{AB}}+3\overrightarrow{\mathrm{BC}}$ = $\overrightarrow{\mathrm{AB}}+3\left(\overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{AB}}\right)$ = $\overrightarrow{\mathrm{AB}}+3\overrightarrow{\mathrm{AC}}-3\overrightarrow{\mathrm{AB}}$ 

= $-2\overrightarrow{\mathrm{AB}}+3\overrightarrow{\mathrm{AC}}$ = –2$\overrightarrow{\mathrm{a}}$ + 3$\overrightarrow{\mathrm{b}}$.

b) Ta có:

$\overrightarrow{\mathrm{AI}}$ = $\overrightarrow{\mathrm{AM}}+\overrightarrow{\mathrm{MI}}$ = $\frac{1}{3}\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{CM}}$ = $\frac{1}{3}$$\overrightarrow{\mathrm{a}}$ + $\frac{1}{3}$$\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$ = $\frac{2}{3}$$\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$ = $-\frac{1}{3}\left(-2\overrightarrow{a}+3\overrightarrow{b}\right)$

⇒ $\overrightarrow{\mathrm{AI}}$ = $-\frac{1}{3}\overrightarrow{\mathrm{AN}}$.

⇒ I, A, N thẳng hàng.

B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ $\overrightarrow{\mathrm{AN}}$, $\overrightarrow{\mathrm{MN}}$, $\overrightarrow{\mathrm{AG}}$ qua các vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{AC}}$.

Hướng dẫn giải:

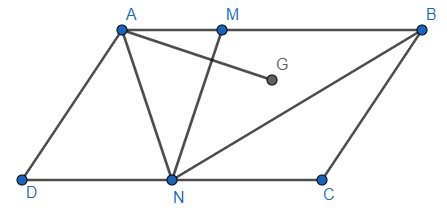
+ Vì ABCD là hình bình hành nên $\overrightarrow{\mathrm{BA}}$ = $\overrightarrow{\mathrm{CD}}$

Ta lại có: CD = 2CN nên N là trung điểm của CD.

Mà $\overrightarrow{\mathrm{CD}}$ và $\overrightarrow{\mathrm{CN}}$ là hai vectơ cùng hướng.

⇒ $\overrightarrow{\mathrm{CD}}=2\overrightarrow{\mathrm{CN}}$.

⇔ $\overrightarrow{\mathrm{CN}}=\frac{1}{2}\overrightarrow{\mathrm{CD}}$ ⟺ $\overrightarrow{\mathrm{CN}}=\frac{1}{2}\overrightarrow{\mathrm{BA}}$ ⟺ $\overrightarrow{\mathrm{CN}}=-\frac{1}{2}\overrightarrow{\mathrm{AB}}$

Suy ra:

$\overrightarrow{\mathrm{AN}}$ = $\overrightarrow{\mathrm{AC}}$ + $\overrightarrow{\mathrm{CN}}$ = $\overrightarrow{\mathrm{AC}}$ – $\frac{1}{2}\overrightarrow{\mathrm{AB}}$

+ Ta có: AB = 3AM ⇒ AM = $\frac{1}{3}$AB

Mà $\overrightarrow{\mathrm{AM}}$ và $\overrightarrow{\mathrm{AB}}$là hai vectơ cùng hướng.

⇒ $\overrightarrow{\mathrm{AM}}=\frac{1}{3}\overrightarrow{\mathrm{AB}}$  

⇒ $\overrightarrow{\mathrm{MA}}=-\frac{1}{3}\overrightarrow{\mathrm{AB}}$

⇒ $\overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{AN}}$ = $-\frac{1}{3}\overrightarrow{\mathrm{AB}}$ + ($\overrightarrow{\mathrm{AC}}$ – $\frac{1}{2}\overrightarrow{\mathrm{AB}}$) = $-\frac{5}{6}\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}$ 

Vì G là trọng tâm tam giác MNB nên:

$3\overrightarrow{\mathrm{AG}}=\overrightarrow{\mathrm{AM}}+\overrightarrow{\mathrm{AN}}+\overrightarrow{\mathrm{AB}}$ = $\frac{1}{3}\overrightarrow{\mathrm{AB}}$ + $\overrightarrow{\mathrm{AC}}$ – $\frac{1}{2}\overrightarrow{\mathrm{AB}}$ + $\overrightarrow{\mathrm{AB}}$= $\frac{5}{6}\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}$

⇒ $\overrightarrow{\mathrm{AG}}=\frac{5}{18}\overrightarrow{\mathrm{AB}}+\frac{1}{3}\overrightarrow{\mathrm{AC}}$

Vậy:

$\overrightarrow{\mathrm{AN}}$ = $\overrightarrow{\mathrm{AC}}$ – $\frac{1}{2}\overrightarrow{\mathrm{AB}}$

$\overrightarrow{\mathrm{MN}}$ = $-\frac{5}{6}\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}$

$\overrightarrow{\mathrm{AG}}=\frac{5}{18}\overrightarrow{\mathrm{AB}}+\frac{1}{3}\overrightarrow{\mathrm{AC}}$

Bài 2. Cho tứ giác ABCD. Gọi M, N lần lượt thuộc các đoạn thẳng AB, CD sao cho MB = 2MA và NC = 2ND. Chứng minh rằng: $\overrightarrow{\mathrm{MN}}=\frac{2}{3}\overrightarrow{\mathrm{AD}}+\frac{1}{3}\overrightarrow{\mathrm{BC}}$.

Hướng dẫn giải:

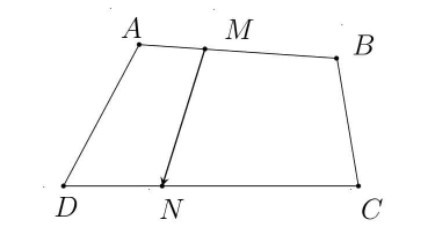
Áp dụng quy tắc cộng vectơ, ta có:

$\overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{DN}}$ (1)

$\overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CN}}$ (2)

Nhân hai vế của phương trình (1) với 2 ta có:

$2\overrightarrow{\mathrm{MN}}=2\overrightarrow{\mathrm{MA}}+2\overrightarrow{\mathrm{AD}}+2\overrightarrow{\mathrm{DN}}$ (3)

Cộng hai vế của (2) và (3) ta có:

$3\overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CN}}+2\overrightarrow{\mathrm{MA}}+2\overrightarrow{\mathrm{AD}}+2\overrightarrow{\mathrm{DN}}$

⇔ $3\overrightarrow{\mathrm{MN}}=\left(2\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}\right)+2\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{BC}}+\left(2\overrightarrow{\mathrm{DN}}+\overrightarrow{\mathrm{CN}}\right)$

Vì M, N lần lượt thuộc các đoạn thẳng AB, CD (M, N lần lượt nằm giữa đoạn thẳng AB và CD).

⇒ $\overrightarrow{\mathrm{MA}},\overrightarrow{\mathrm{MB}}$và $\overrightarrow{\mathrm{DN}},\overrightarrow{\mathrm{CN}}$ là hai cặp vectơ ngược hướng.

 Mà MB = 2MA và NC = 2ND nên ta có:

$2\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}=\overrightarrow{0}$ 

$2\overrightarrow{\mathrm{DN}}+\overrightarrow{\mathrm{CN}}=\overrightarrow{0}$ 

Suy ra:

$3\overrightarrow{\mathrm{MN}}=2\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{BC}}$

⇒ $\overrightarrow{\mathrm{MN}}=\frac{2}{3}\overrightarrow{\mathrm{AD}}+\frac{1}{3}\overrightarrow{\mathrm{BC}}$ (đpcm).

Bài 3. Cho tam giác ABC có P là trung điểm của AB và hai điểm M, N thỏa mãn các hệ thức: $\overrightarrow{\mathrm{MB}}=2\overrightarrow{\mathrm{MC}}$;$\overrightarrow{\text{AN}}=2\overrightarrow{\mathrm{NC}}$.

Chứng minh ba điểm M, N, P thẳng hàng.

Hướng dẫn giải:

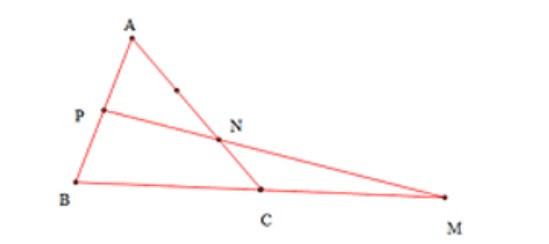
Vì:

+) $\overrightarrow{\text{AN}}=2\overrightarrow{\mathrm{NC}}$

Nên AN = 2NC ⇒ CN = $\frac{1}{3}$CA.

Mà $\overrightarrow{\mathrm{CN}}$ và $\overrightarrow{\mathrm{CA}}$ là hai vectơ cùng hướng.

⇒ $\overrightarrow{\mathrm{CN}}=\frac{1}{3}\overrightarrow{\mathrm{CA}}$ .

+) $\overrightarrow{\mathrm{MB}}=2\overrightarrow{\mathrm{MC}}$ ⇒ MB = 2MC ⇒ C là trung điểm của MB.

⇒ MC = CB

Mà $\overrightarrow{\mathrm{MC}}$ và $\overrightarrow{\mathrm{CB}}$ là hai vectơ cùng hướng.

⇒ $\overrightarrow{\mathrm{MC}}=\overrightarrow{\mathrm{CB}}$

⇒ $\overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{MC}}+\overrightarrow{\mathrm{CN}}$ = $\overrightarrow{\mathrm{CB}}+\frac{1}{3}\overrightarrow{\mathrm{CA}}$

⇒ $3\overrightarrow{\mathrm{MN}}=3\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{CA}}$ (1)

Ta lại có:

+) C là trung điểm của MB ⇒ $\overrightarrow{\mathrm{MB}}=2\overrightarrow{\mathrm{CB}}$

+) P là trung điểm của AB ⇒ $\overrightarrow{\mathrm{BP}}=\frac{1}{2}\overrightarrow{\mathrm{BA}}$

⇒ $\overrightarrow{\mathrm{MP}}=\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{BP}}$ = $2\overrightarrow{\mathrm{CB}}+\frac{1}{2}\overrightarrow{\mathrm{BA}}$ = $2\overrightarrow{\mathrm{CB}}+\frac{1}{2}\left(\overrightarrow{\mathrm{CA}}-\overrightarrow{\mathrm{CB}}\right)$ 

= $2\overrightarrow{\mathrm{CB}}+\frac{1}{2}\overrightarrow{\mathrm{CA}}-\frac{1}{2}\overrightarrow{\mathrm{CB}}$ = $\frac{3}{2}\overrightarrow{\mathrm{CB}}+\frac{1}{2}\overrightarrow{\mathrm{CA}}$

⇒ $2\overrightarrow{\mathrm{MP}}=3\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{CA}}$ (2)

Từ (1) và (2) ta có:

$3\overrightarrow{\mathrm{MN}}=2\overrightarrow{\mathrm{MP}}$ ⇔ $\overrightarrow{\mathrm{MN}}=\frac{2}{3}\overrightarrow{\mathrm{MP}}$

Do đó ba điểm M, N, P thẳng hàng (đpcm).

B.2 Bài tập trắc nghiệm

Câu 1. Cho tam giác ABC có M là trung điểm của BC, I là trung điểm của AM. Khẳng định nào sau đây đúng ?

A. $\overrightarrow{\mathrm{AI}}=\frac{1}{4}\left(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}\right);$  

B. $\overrightarrow{\mathrm{AI}}=\frac{1}{4}\left(\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AC}}\right);$  

C. $\overrightarrow{\mathrm{AI}}=\frac{1}{4}\overrightarrow{\mathrm{AB}}+\frac{1}{2}\overrightarrow{\mathrm{AC}};$  

D. $\overrightarrow{\mathrm{AI}}=\frac{1}{4}\overrightarrow{\mathrm{AB}}-\frac{1}{2}\overrightarrow{\mathrm{AC}}.$

Hướng dẫn giải

Đáp án đúng là: A

Vì M là trung điểm BC nên $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}=2\overrightarrow{\mathrm{AM}}.$ (1)

Mặt khác I là trung điểm AM nên $2\overrightarrow{\mathrm{AI}}=\overrightarrow{\mathrm{AM}}.$ (2)

Từ (1), (2) suy ra $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}=4\overrightarrow{\mathrm{AI}}\iff \overrightarrow{\mathrm{AI}}=\frac{1}{4}\left(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}\right).$

Câu 2. Cho tứ giác ABCD. Trên cạnh AB, CD lấy lần lượt các điểm M, N sao cho $3\overrightarrow{\mathrm{AM}}=2\overrightarrow{\mathrm{AB}}$ và $3\overrightarrow{\mathrm{DN}}=2\overrightarrow{\mathrm{DC}}.$ Tính vectơ $\overrightarrow{\mathrm{MN}}$ theo hai vectơ $\overrightarrow{\mathrm{AD}},\overrightarrow{\mathrm{BC}}.$

A. $\overrightarrow{\mathrm{MN}}=\frac{1}{3}\overrightarrow{\mathrm{AD}}+\frac{1}{3}\overrightarrow{\mathrm{BC}};$                                   

B. $\overrightarrow{\mathrm{MN}}=\frac{1}{3}\overrightarrow{\mathrm{AD}}-\frac{2}{3}\overrightarrow{\mathrm{BC}};$

C. $\overrightarrow{\mathrm{MN}}=\frac{1}{3}\overrightarrow{\mathrm{AD}}+\frac{2}{3}\overrightarrow{\mathrm{BC}};$                                   

D. $\overrightarrow{\mathrm{MN}}=\frac{2}{3}\overrightarrow{\mathrm{AD}}+\frac{1}{3}\overrightarrow{\mathrm{BC}}.$

Hướng dẫn giải

Đáp án đúng là: C

Ta có: $\overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{DN}}$ và $\overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CN}}.$ 

Suy ra $3\overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{DN}}+2\left(\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CN}}\right)$

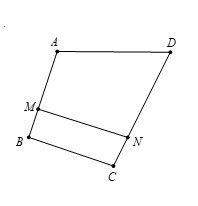
    $=\left(\overrightarrow{\mathrm{MA}}+2\overrightarrow{\mathrm{MB}}\right)+\left(\overrightarrow{\mathrm{AD}}+2\overrightarrow{\mathrm{BC}}\right)+\left(\overrightarrow{\mathrm{DN}}+2\overrightarrow{\mathrm{CN}}\right).$

Theo bài ra, ta có:  

+) $3\overrightarrow{\mathrm{AM}}=2\overrightarrow{\mathrm{AB}}\iff 3\overrightarrow{\mathrm{AM}}=2\left(\overrightarrow{\mathrm{AM}}+\overrightarrow{\mathrm{MB}}\right)$$\iff 3\overrightarrow{\mathrm{AM}}=2\overrightarrow{\mathrm{AM}}+2\overrightarrow{\mathrm{MB}}$

$\iff \overrightarrow{\mathrm{AM}}=2\overrightarrow{\mathrm{MB}}$$\iff 2\overrightarrow{\mathrm{MB}}-\overrightarrow{\mathrm{AM}}=\overrightarrow{0}$$\iff 2\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MA}}=\overrightarrow{0}$.

+)$3\overrightarrow{\mathrm{DN}}=2\overrightarrow{\mathrm{DC}}\iff 3\overrightarrow{\mathrm{DN}}=2(\overrightarrow{\mathrm{DN}}+\overrightarrow{\mathrm{NC}})$ $\iff 3\overrightarrow{\mathrm{DN}}=2\overrightarrow{\mathrm{DN}}+2\overrightarrow{\mathrm{NC}}$

$\iff \overrightarrow{\mathrm{DN}}=2\overrightarrow{\mathrm{NC}}$$\iff \overrightarrow{\mathrm{DN}}-2\overrightarrow{\mathrm{NC}}=\overrightarrow{0}$$\iff \overrightarrow{\mathrm{DN}}+2\overrightarrow{\mathrm{CN}}=\overrightarrow{0}$.

Vậy $3\overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{AD}}+2\overrightarrow{\mathrm{BC}}\iff \overrightarrow{\mathrm{MN}}=\frac{1}{3}\overrightarrow{\mathrm{AD}}+\frac{2}{3}\overrightarrow{\mathrm{BC}}.$

Câu 3. Cho hình bình hành ABCD có M là trung điểm của AB. Khẳng định nào sau đây đúng?

A. $\overrightarrow{\mathrm{DM}}=\frac{1}{2}\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{BC}};$   

B. $\overrightarrow{\mathrm{DM}}=\frac{1}{2}\overrightarrow{\mathrm{CD}}-\overrightarrow{\mathrm{BC}};$   

C. $\overrightarrow{\mathrm{DM}}=\frac{1}{2}\overrightarrow{\mathrm{DC}}-\overrightarrow{\mathrm{BC}};$   

D. $\overrightarrow{\mathrm{DM}}=\frac{1}{2}\overrightarrow{\mathrm{DC}}+\overrightarrow{\mathrm{BC}}.$

Hướng dẫn giải

Đáp án đúng là: C

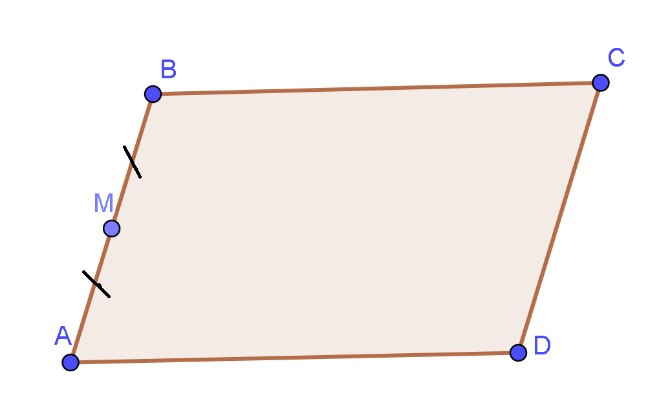
Xét các đáp án ta thấy cần phân tích vectơ $\overrightarrow{\mathrm{DM}}$ theo hai vectơ $\overrightarrow{\mathrm{DC}}$ và $\overrightarrow{\mathrm{BC}}.$

Vì ABCD là hình bình hành nên $\overrightarrow{\mathrm{DB}}=\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{DC}}.$

Và M là trung điểm AB nên $2\overrightarrow{\mathrm{DM}}=\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{DB}}$

$\iff 2\overrightarrow{\mathrm{DM}}=\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{DC}}$

$\iff 2\overrightarrow{\mathrm{DM}}=2\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{DC}}.$

$\iff 2\overrightarrow{\mathrm{DM}}=-2\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{DC}}$  (do $\overrightarrow{\mathrm{DA}}=-\overrightarrow{\mathrm{BC}}$)

Suy ra $\overrightarrow{\mathrm{DM}}=\frac{1}{2}\overrightarrow{\mathrm{DC}}-\overrightarrow{\mathrm{BC}}.$

Xem thêm các bài tóm tắt lý thuyết Toán lớp 10 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 4: Tổng và hiệu của hai vectơ

Lý thuyết Bài 5: Tích của một số với một vectơ

Lý thuyết Bài 6: Tích vô hướng của hai vectơ

Lý thuyết Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây

Lý thuyết Bài 2: Hoán vị. Chỉnh hợp

Bài giảng Toán 10 Bài 5: Tích của một số với một vectơ – Cánh diều