Lý thuyết Toán lớp 10 Bài 6: Tích vô hướng của hai vectơ
Video giải Toán 10 Bài 6: Tích vô hướng của hai vectơ – Cánh diều
A. Lý thuyết Tích vô hướng của hai vectơ
1. Định nghĩa
1.1. Tích vô hướng của hai vectơ có cùng điểm đầu
– Góc giữa hai vectơ , là góc giữa hai tia OA, OB và được kí hiệu là
– Tích vô hướng của hai vectơ và là một số thực, kí hiệu là ., được xác định bởi công thức: .
Ví dụ: Cho tam giác ABC đều cạnh 2a có đường cao AH. Tính tích vô hướng của .
Hướng dẫn giải:
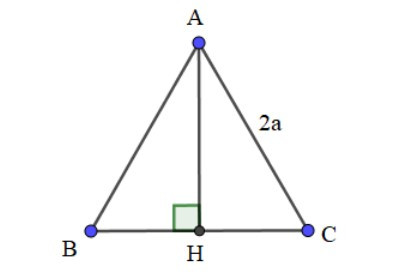
Vì tam giác ABC đều nên = 60°
⇒ = = 60°
Ta có:
=
⇒ = AB.AC.cos = AB.AC.cos60° = 2a.2a. = 2a2.
1.2. Tích vô hướng của hai vectơ tùy ý
Định nghĩa:
Cho hai vectơ , khác Lấy một điểm O và vẽ vectơ (Hình vẽ).
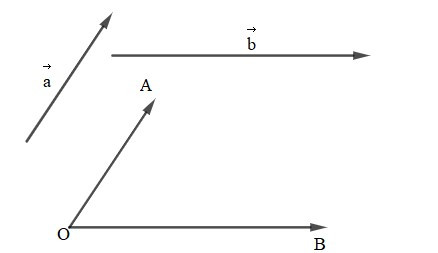
+ Góc giữa hai vectơ , , kí hiệu , là góc giữa hai vectơ , .
+ Tích vô hướng của hai vectơ và , kí hiệu . là tích vô hướng của hai vectơ và . Như vậy, tích vô hướng của hai vectơ và là một số thực được xác định bởi công thức: . = .
Quy ước: Tích vô hướng của một vectơ bất kì với vectơ là số 0.
Chú ý:
+) =
+) Nếu = 90° thì ta nói hai vectơ , vuông góc với nhau, kí hiệu ⊥ hoặc ⊥ . Khi đó . = = 0.
+) Tích vô hướng của hai vectơ cùng hướng bằng tích hai độ dài của chúng.
+) Tích vô hướng của hai vectơ ngược hướng bằng số đối của tích hai độ dài của chúng.
Ví dụ: Cho tam giác vuông cân ABC có AB = AC = a. Tính các tích vô hướng ,.
Hướng dẫn giải:
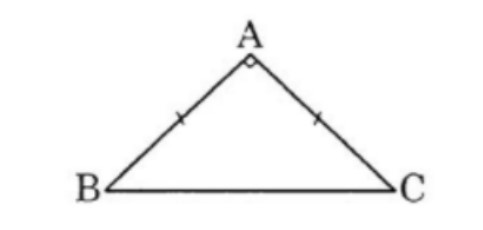
+ Vì tam giác ABC vuông cân, mà AB = AC
⇒ Tam giác ABC vuông cân tại A.
⇒ AB ⊥ AC
⇒ = = = 0
+ Ta có: BC = = = a.
⇒ = = a. a.cos135° = a. a. = –a2.
2. Tính chất
Với hai vectơ bất kì , và số thực k tùy ý, ta có:
+) . = . (tính chất giao hoán);
+) (tính chất phân phối);
+) ;
+) ≥ 0, = 0 ⟺ = .
Trong đó, kí hiệu . = và biểu thức này được gọi là bình phương vô hướng của vectơ .
Ví dụ: Cho 4 điểm A, B, C, D bất kì. Chứng minh: .
Hướng dẫn giải:
Ta có:
= = (tính chất phân phối)
= = = (tính chất phân phối)
= = = (tính chất phân phối)
= (tính chất giao hoán và kết hợp)
= 0
⟺ (đpcm).
3. Một số ứng dụng
3.1. Tính độ dài của đoạn thẳng
Nhận xét:
Với hai điểm A, B phân biệt, ta có: .
Do đó độ dài đoạn thẳng AB được tính như sau: AB =
3.2. Chứng minh hai đường thẳng vuông góc
Nhận xét:
+ Cho hai vectơ bất kì và khác vectơ . Ta có: . = 0 ⟺ ⊥ .
Hai đường thẳng AB và CD vuông góc với nhau khi và chỉ khi + Hai đường thẳng a và b vuông góc khi và chỉ khi , trong đó ≠ 0, ≠ 0, giá của vectơ song song hoặc trùng với đường thẳng a và giá của vectơ song song hoặc trùng với đường thẳng b.
Ví dụ: Cho hai vectơ và vuông góc với nhau và , . Chứng minh hai vectơ 2 – và + vuông góc với nhau.
Hướng dẫn giải:
Vì và vuông góc với nhau ⟺ . = 0
Ta có:
= = =
= 2.12 + 0 – = 0
Vì tích của hai vectơ 2 – và + bằng 0 nên chúng vuông góc với nhau.
B. Bài tập tự luyện
B.1 Bài tập tự luận
Bài 1. Cho đoạn thẳng AB có trung điểm O, điểm M tùy ý khác O, A, B và không thuộc AB, biết 4OM2 = AB2. Sử dụng các kiến thức về vectơ, chứng minh MA ⊥ MB.
Hướng dẫn giải:
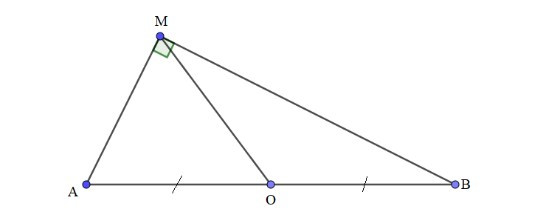
Ta có:
4OM2 = AB2 ⟺ (2OM)2 = AB2
⇔
⇔
⇔
⇔
⇔
⇔
⇔
⇔
⇒ ⇒ MA ⊥ MB (đpcm).
Bài 2. Cho tam giác ABC bất kì có I là trung điểm của AB. Chứng minh đẳng thức:
CA2 + CB2 = 2CI2 + .
Hướng dẫn giải:

Ta có:
VP = 2CI2 +
⇔ 2VP = 4CI2 + AB2
⇔ 2VP= (2CI)2 + AB2
⇔ 2VP =
⇔ 2VP =
⇔ 2VP =
⇔ 2VP =
⇔ 2VP =
⇔ 2VP = = VT
⇒ CA2 + CB2 = 2CI2 + (đpcm).
Bài 3. Cho tam giác ABC, biết AB = a, AC = 2a, = 60°. Sử dụng các kiến thức về vectơ, tính độ dài cạnh BC.
Hướng dẫn giải:
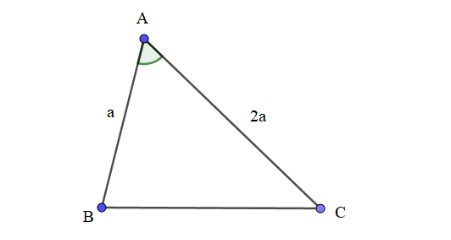
Áp dụng quy tắc hiệu hai vectơ ta có:
⇒ =
Ta có:
= AC2 = (2a)2 = 4a2
= AB2 = a2
= = AC.AB.cos = 2a.a.cos60° = 2.a.a. = a2
⇒ = 4a2 – 2a2 + a2 = 3a2
⇒ BC2 = = = 3a2
⇒ BC = = .
B.2 Bài tập trắc nghiệm
Câu 1. Cho và khác vectơ . Xác định góc giữa hai vectơ và khi
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là: A
Ta có: .
Mà theo giả thiết , suy ra
Câu 2. Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là: D
Xác định được góc là góc nên (do tam giác ABC đều)
Do đó
Câu 3. Cho tam giác ABC có BC = a, CA = b, AB = c. Gọi M là trung điểm cạnh BC Tính
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là: A
Vì M là trung điểm của BC suy ra
Khi đó
Xem thêm các bài tóm tắt lý thuyết Toán lớp 10 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 5: Tích của một số với một vectơ
Lý thuyết Bài 6: Tích vô hướng của hai vectơ
Lý thuyết Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây
Lý thuyết Bài 2: Hoán vị. Chỉnh hợp
Lý thuyết Bài 3: Tổ hợp
Bài giảng Toán 10 Bài 6: Tích vô hướng của hai vectơ – Cánh diều