Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu bao gồm các nội dung sau:
– Vecto, tích vô hướng và ứng dụng chứng minh tính chất hình học.
– Giải Oxy bằng tham số hóa
– Chuẩn hóa các đại lượng trong Oxy
Một số phương pháp giải bài toán hình học tọa độ phẳng Oxy
Chuyên đề casio
Kỹ năng giải hình học phẳng oxy trong đề thi THPT quốc gia
A – Giới Thiệu :
Là một dạng bài toán yêu cầu tư duy hình học cao, Oxy trong kỳ thi THPT Quốc Gia thường được cho dưới dạng tọa độ và yêu cầu của đề bài là đi tìm một dữ kiện nào đó của hình học, có thể là tìm tọa độ điểm, phương trình đường thẳng,
Tuy nhiên, những bài tập Oxy này có một sự liên kết không hề nhẹ với phần hình học phẳng lớp 8, lớp 9 qua các định lý, tính chất hình học. Nhiều bạn chưa biết đến những tính chất này chắc hẳn sẽ vô cùng hoang mang vì không biết hướng giải quyết. Và chắc chắn cũng sẽ có những bạn biết đến tính chất này nhưng không biết cách chứng minh thế nào.
Để giúp những bạn có tư duy hình học kém hoặc biết tính chất hình học nhưng chưa biết cách chứng minh, chuyên đề này sẽ gồm các phần như sau:
– Vecto, tích vô hướng và ứng dụng chứng minh tính chất hình học.
– Giải Oxy bằng tham số hóa
– Chuẩn hóa các đại lượng trong Oxy
Để phù hợp với kiến thức thi THPT Quốc Gia, chuyên đề này đa phân lấy bài tập từ đề thi thử các trường THPT trên toàn quốc năm 2016 .
B – Nội dung:
Vecto và tích vô hướng là các kiến thức cơ bản của THPT. Để ứng dụng nó vào việc chứng minh các tính chất hình học, chúng ta cần phải biết những công thức, định lý hay dùng sau:
\({\rm{AB}} \Leftrightarrow \overrightarrow {{\rm{AB}}} + \overrightarrow {{\rm{AC}}} = 2\overrightarrow {{\rm{AM}}} \)
– \(\overrightarrow {{\rm{AB}}} \overrightarrow {{\rm{AC}}} = |\overrightarrow {{\rm{AB}}} ||\overrightarrow {{\rm{AC}}} |\cos {\rm{BAC}}\)
– \(\overrightarrow {{\rm{AB}}} \overrightarrow {{\rm{AC}}} = \frac{{{\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} – {\rm{B}}{{\rm{C}}^2}}}{2}\)
– \(\overrightarrow {{\rm{AB}}} \bot \overrightarrow {{\rm{AC}}} \Leftrightarrow \overrightarrow {{\rm{AB}}} \overrightarrow {{\rm{AC}}} = 0\)
Vậy phương pháp chứng minh tính chất hình học của chúng ta là:
> Cố gắng đưa dữ kiện cân phải chứng minh dưới dạng vecto.
> Tách vecto thành tổng các vecto thành phần rồi sử dụng tích vô hướng hoặc các tính chất của vecto để giải quyết bài toán.
Ví dụ 1 : Cho tam giác ABC nội tiếp đường tròn \(({\rm{I}})\) : \({(x – 1)^2} + {(y + 2)^2} = 25\). Điểm \({\rm{H}}(2; – 5)\) và \({\rm{K}}( – 1; – 1)\) lần lượt là chân các đường cao hạ từ đỉnh B và C đến các cạnh tam giác. Tìm tọa độ các đỉnh A,B,C của tam giác biết A có hoành độ dương.
(THPT Chuyên Sơn La – Sơn La – lần 3 – 2016)
Hướng dẫn
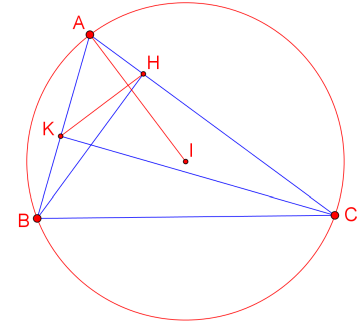
Ý tưởng : Chứng minh AI vuông góc KH
Chứng minh :
Cách 1 : (Sử dụng Vecto và tích vô hướng).
Ta có :
\(\)\[\begin{array}{*{20}{c}}{\overrightarrow {{\rm{AIKH}}} = (\overrightarrow {{\rm{KA}}} + \overrightarrow {{\rm{AH}}} )\overrightarrow {{\rm{AI}}} = \overrightarrow {{\rm{KA}}} \overrightarrow {{\rm{AI}}} + \overrightarrow {{\rm{AH}}} \overrightarrow {{\rm{AI}}} }\\{ = – {\rm{AK}} \cdot {\rm{AI}} \cdot \cos {\rm{KAI}} + {\rm{AH}} \cdot {\rm{AI}} \cdot \cos {\rm{HAI}}}\\{ = – {\rm{AK}} \cdot {\rm{AI}} \cdot \frac{{{\rm{AB}}}}{{2{\rm{AI}}}} + {\rm{AH}} \cdot {\rm{AI}} \cdot \frac{{{\rm{AC}}}}{{2{\rm{AI}}}}}\\{ = – \frac{1}{2}({\rm{AK}} \cdot {\rm{AB}} – {\rm{AH}} \cdot {\rm{AC}}) = 0}\end{array}\]
\[\begin{array}{l}{\rm{\;Do\;\Delta ABH}} \sim {\rm{\Delta ACK}}\\ \Rightarrow \frac{{{\rm{AB}}}}{{{\rm{AC}}}} = \frac{{{\rm{AH}}}}{{{\rm{AK}}}}\\ \Rightarrow {\rm{AK}} \cdot {\rm{AB}} = {\rm{AH}} \cdot {\rm{AC}}\end{array}\]
Cách 2: ( Sử dụng kiến thức hình học THCS).
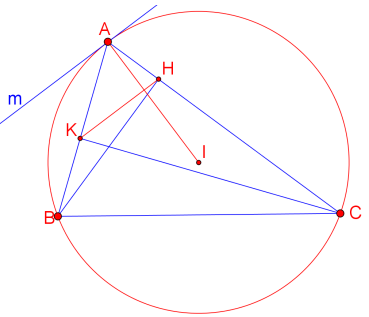
Qua A, kẻ tia tiếp tuyến Am với (I), H không thuộc nửa mặt phẳng bờ AI chứa Am. Khi đó \({\rm{AI}} \bot {\rm{Am}}\).
Ta chỉ cần chứng minh \({\rm{HK}}//{\rm{Am}}\).
Thật vậy, \({\rm{BAm}} = {\rm{BCA}} = {\rm{AKH}}\) do tứ giác \({\rm{BCHK}}\) nội tiếp. Suy ra \({\rm{HK}}//{\rm{Am}}\). Điều phải chứng minh.
Áp dụng : Ta lần lượt tính được :
– Phương trình đường thẳng \({\rm{KH}}:4x + 3y + 7 = 0\)
– Phương trình đường thẳng \({\rm{AI}}\) : \(3x – 4y – 11 = 0\)
– Tọa độ điểm \({\rm{A}}(5,1)\) (điểm \(( – 3, – 5)\) bị loại)
– Phương trình đường thẳng \({\rm{AK}}:{\rm{x}} – 3{\rm{y}} – 2 = 0\)
– Tọa độ điểm \(B( – 4, – 2)\)
– Phương trình đường thẳng \({\rm{AH}}:2x – y – 9 = 0\)
– Tọa độ điểm \(C(1, – 7)\)
Lời giải chi tiết dành cho bạn đọc.
Đáp số : \({\rm{A}}(5,1),{\rm{B}}( – 4, – 2),{\rm{C}}(1, – 7)\).
Nhận xét : Qua hai cách làm, chúng ta thấy rằng : Chứng minh bằng kiến thức hình học THCS trông gọn và đẹp hơn nhiều so với cách 1 sử dụng vecto và tích vô hướng. Tuy nhiên, không phải ai cũng nghĩ tới việc kẻ thêm đường kẻ phụ Am như trên. Cái đó phụ thuộc vào tư duy hình học và cả kinh nghiệm làm bài.
Cách giải bằng vecto và tích vô hướng tuy không tự nhiên bằng nhưng chắc chắn sau khi biến đổi, vấn đề của bài toán luôn được chứng minh mặc dù có thể lời giải không được đẹp cho lắm. Bạn đọc thử đến với ví dụ 2 :
Ví dụ 2 : Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có điểm \({\rm{H}}( – 3,1)\) là hình chiếu vuông góc của A trên BD. Điểm \({\rm{M}}\left( {\frac{1}{2},2} \right)\) là trung điểm cạnh BC, phương trình đường trung tuyến kẻ từ đỉnh A của tam giác ADH là \({\rm{d}}:4x + {\rm{y}} + 13 = 0\). Viết phương trình đường thẳng BC.
(THPT Đoàn Thượng – Hải Phòng – lân 3-2016)
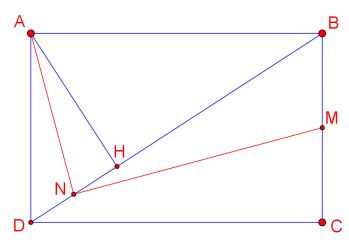
Ý tưởng : Gọi N là trung điểm DH. Chứng minh AN vuông góc NM.
Chứng minh :
Cách 1 : (Sử dụng Vecto và tích vô hướng).
Ta có :
\(\overrightarrow {{\rm{ANNM}}} = (\overrightarrow {{\rm{AB}}} + \overrightarrow {{\rm{BN}}} )(\overrightarrow {{\rm{NB}}} + \overrightarrow {{\rm{BM}}} )\)
\( = \overrightarrow {{\rm{AB}}NB} + \overrightarrow {{\rm{AB}}BM} + \overrightarrow {{\rm{BNNB}}} + \overrightarrow {{\rm{BN}}} \overrightarrow {{\rm{BM}}} \)
\( = \overrightarrow {{\rm{NB}}} (\overrightarrow {{\rm{AB}}} + \overrightarrow {{\rm{BN}}} – \overrightarrow {{\rm{BM}}} ) = \overrightarrow {{\rm{NB}}} (\overrightarrow {{\rm{AN}}} – \overrightarrow {{\rm{BM}}} )\)
\( = \frac{1}{2}\overrightarrow {{\rm{NB}}} (\overrightarrow {{\rm{AD}}} + \overrightarrow {{\rm{AH}}} – \overrightarrow {{\rm{AD}}} ) = \frac{1}{2}\overrightarrow {{\rm{NB}}} \overrightarrow {{\rm{AH}}} = 0\)
Cách 2: ( Sử dụng kiến thức hình học THCS).
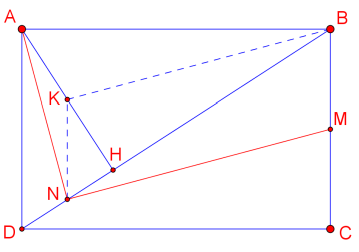
Gọi K là trung điểm AH. Khi đó \(\left\{ {\begin{array}{*{20}{l}}{{\rm{NK}} = \frac{1}{2}{\rm{AD}} = \frac{1}{2}{\rm{BC}} = {\rm{BM}}}\\{{\rm{NK}}//{\rm{CD}}//{\rm{BM}}}\end{array} \Rightarrow {\rm{BMNK}}} \right.\) là hình bình hành. Suy ra \({\rm{BK}}//{\rm{NM}}\). Vậy để chứng minh \({\rm{AN}} \bot {\rm{NM}}\), ta chỉ cân chứng minh \({\rm{BK}} \bot {\rm{AN}}\).
Do \(\left\{ {\begin{array}{*{20}{l}}{{\rm{NK}} \bot {\rm{AB}}}\\{{\rm{AK}} \bot {\rm{NB}}}\end{array} \Rightarrow {\rm{K}}} \right.\) là trực tâm \(\Delta {\rm{ABN}}\). Suy ra \({\rm{BK}} \bot {\rm{AN}}\). Điều phải chứng minh.
Áp dụng : Ta lần lượt tính được :
– Phương trình đường thẳng \({\rm{MN}}:2x – 8y + 15 = 0\)
– Phương trình đường thẳng \({\rm{BD}}:{\rm{y}} = 1\)
– Tọa độ điểm \({\rm{D}}( – 4,1)\)
– Phương trình đường thẳng \({\rm{HA}}:{\rm{x}} = – 3\)
– Tọa độ điểm \({\rm{A}}( – 3, – 1)\)
– Phương trình đường thẳng \({\rm{AD}}:2{\rm{x}} + {\rm{y}} + 7 = 0\)
– Phương trình đường thẳng \({\rm{AB}}:{\rm{x}} – 2{\rm{y}} + 1 = 0\)
– Tọa độ điểm \(B(1,1)\)
– Phương trình đường thẳng \({\rm{BC}}:2{\rm{x}} + {\rm{y}} – 3 = 0\)
Lời giải chi tiết dành cho bạn đọc.
Đáp số : \(2x + y – 3 = 0\).
Nhận xét : Tại sao trong cách 1, chúng ta lại tách thành \(\overrightarrow {{\rm{AN}}} \overrightarrow {{\rm{NM}}} = (\overrightarrow {{\rm{AB}}} + \overrightarrow {{\rm{BN}}} )(\overrightarrow {{\rm{NB}}} + \overrightarrow {{\rm{BM}}} )\).
Thực chất thì dù tách thành cái gì, sau một hồi biến đổi, kiểu gì chúng ta cũng sẽ làm triệt tiêu được các vecto thành phần. Ví dụ như cách biến đổi sau đây :
\(\overrightarrow {{\rm{ANNM}}} = \frac{1}{2}(\overrightarrow {{\rm{AD}}} + \overrightarrow {{\rm{AH}}} )(\overrightarrow {{\rm{NB}}} + \overrightarrow {{\rm{BM}}} )\)
\( = \frac{1}{2}(\overrightarrow {{\rm{AD}}} + \overrightarrow {{\rm{AH}}} ) \cdot \frac{1}{2}(\overrightarrow {{\rm{DB}}} + \overrightarrow {{\rm{HB}}} + \overrightarrow {{\rm{AD}}} )\)
\( = \frac{1}{4}(\overrightarrow {{\rm{ADDB}}} + \overrightarrow {{\rm{AD}}} \overrightarrow {{\rm{HB}}} + \overrightarrow {{\rm{AD}}} \overrightarrow {{\rm{AD}}} + \overrightarrow {{\rm{AH}}} \overrightarrow {{\rm{AD}}} )\)
\( = \frac{{{\rm{AD}}}}{4}(\overline {{\rm{DB}}} + \overrightarrow {{\rm{HB}}} + \overrightarrow {{\rm{AD}}} + \overrightarrow {{\rm{AH}}} )\)
\( = \frac{{\overrightarrow {{\rm{AD}}} }}{4}(2\overrightarrow {{\rm{NB}}} + 2\overrightarrow {{\rm{AN}}} ) = \frac{{\overrightarrow {{\rm{AD}}\overrightarrow {{\rm{AB}}} } }}{2} = 0\)
Vậy tại sao tách \(\overrightarrow {{\rm{AN}}} \overrightarrow {{\rm{NM}}} = (\overrightarrow {{\rm{AB}}} + \overrightarrow {{\rm{BN}}} )(\overrightarrow {{\rm{NB}}} + \overrightarrow {{\rm{BM}}} )\) lại nhanh như vậy?
Chúng ta có một mẹo như sau :
Nếu \({\rm{AB}} \bot {\rm{AC}} \Leftrightarrow \overrightarrow {{\rm{AB}}} {\rm{AC}} = 0\) mà ta muốn lấy tích vô hướng của \(\overrightarrow {{\rm{MB}}} \overrightarrow {{\rm{MC}}} \), ta cố gắng biến đổi về \(\overrightarrow {{\rm{ABAC}}} \). Mẹo sau rất hay dùng :
\( = (\overrightarrow {{\rm{MA}}} + \overrightarrow {{\rm{AB}}} )(\overrightarrow {{\rm{MA}}} + \overrightarrow {{\rm{AC}}} ) = \overrightarrow {{\rm{MA}}} \overrightarrow {{\rm{MA}}} + \overrightarrow {{\rm{MA}}} \overrightarrow {{\rm{AC}}} + \overrightarrow {{\rm{ABMA}}} + \overrightarrow {{\rm{AB}}} \overrightarrow {{\rm{AC}}} = \overrightarrow {{\rm{MA}}} (\overrightarrow {{\rm{MC}}} + \overrightarrow {{\rm{AB}}} )\)
Tiếp theo ta có hai hướng giải
– Biến đổi \[\overrightarrow {{\rm{MC}}} + \overrightarrow {{\rm{AB}}} = \overrightarrow {{\rm{XY}}} \] và sau đó chứng minh \(\overrightarrow {{\rm{MAXY}}} = 0\)
– Dùng công thức \(\overrightarrow {{\rm{AB}}} \overrightarrow {{\rm{AC}}} = \frac{{{\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} – {\rm{B}}{{\rm{C}}^2}}}{2}\) hoặc đế tính giá trị \(\overrightarrow {{\rm{MAMC}}} + \overrightarrow {{\rm{MAAB}}} \) rồi cố gắng biến đổi \(\overrightarrow {{\rm{MAMC}}} + \overrightarrow {{\rm{MAAB}}} = 0\)
Xem thêm