Cho điểm A nằm ngoài đường thẳng a, quan sát cách vẽ đường thẳng b đi qua A và song song với a ở Hình 8. Em hãy dự đoán xem có tất cả bao nhiêu đường thẳng b đi qua A và song song với đường thẳng a.

Câu hỏi:

Cho điểm A nằm ngoài đường thẳng a, quan sát cách vẽ đường thẳng b đi qua A và song song với a ở Hình 8.

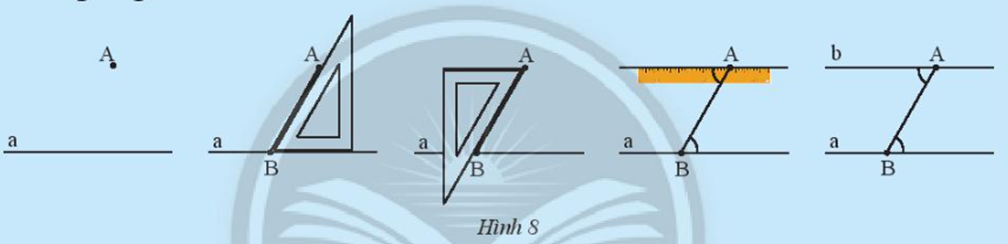
Em hãy dự đoán xem có tất cả bao nhiêu đường thẳng b đi qua A và song song với đường thẳng a.

Trả lời:

Vẽ hình theo các bước như trên Hình 8.
Dự đoán: có một đường thẳng b đi qua A và song song với đường thẳng a.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. – Hai đường thẳng a và b không có điểm nào chung thì được gọi là hai đường thẳng song song và được kí hiệu là a // b hoặc b // a. – Có dấu hiệu gì về số đo của các góc đỉnh A và các góc đỉnh B trong hình bên để nhận biết hai đường thẳng a và b song song hay không?
   
   

   Câu hỏi:
   

   – Hai đường thẳng a và b không có điểm nào chung thì được gọi là hai đường thẳng song song và được kí hiệu là a // b hoặc b // a.
   – Có dấu hiệu gì về số đo của các góc đỉnh A và các góc đỉnh B trong hình bên để nhận biết hai đường thẳng a và b song song hay không?
   

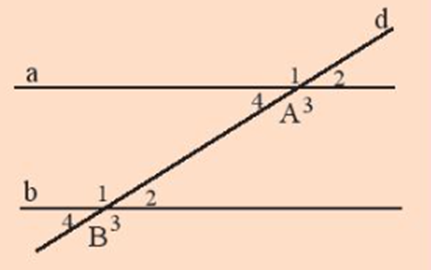
   Trả lời:

   Đo lần lượt các góc tạo bởi ba đường thẳng a, b, d, ta thấy:
   ${\widehat{A}}_1={\widehat{A}}_3={\widehat{B}}_1={\widehat{B}}_3={30}^o$
   ${\widehat{A}}_2={\widehat{A}}_4={\widehat{B}}_2={\widehat{B}}_4={150}^o$.
   Để biết dấu hiệu về số đo của các góc đỉnh A và các góc đỉnh B trong hình trên để a // b thì ta cùng tìm hiểu mục I trang 76.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

2. Quan sát Hình 3 và dự đoán các đường thẳng nào song song với nhau.
   
   

   Câu hỏi:
   

   Quan sát Hình 3 và dự đoán các đường thẳng nào song song với nhau.
   

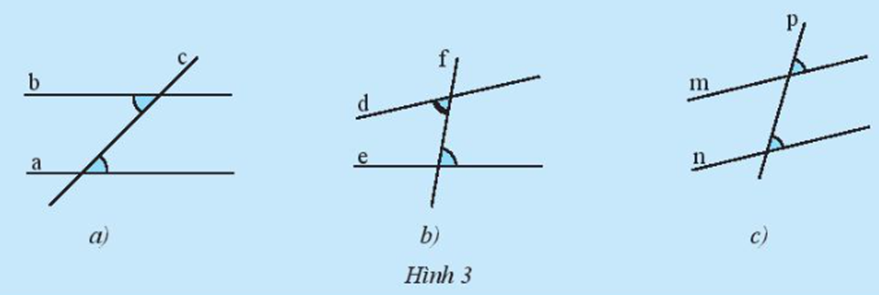
   Trả lời:

   – Hình 3a: Giả sử đường thẳng a, b với đường thẳng c lần lượt tại hai điểm A và B.
   

   Ta có: ${\widehat{A}}_1={\widehat{B}}_1$.
   Dự đoán: Đường thẳng a song song với b.
   – Hình 3b: Giả sử đường thẳng d, e với đường thẳng f lần lượt tại hai điểm D và E.
   

   Ta có: ${\widehat{D}}_1\ne {\widehat{E}}_1$.
   Dự đoán: Đường thẳng d không song song với e.
   – Hình 3c: Giả sử đường thẳng m, n với đường thẳng p lần lượt tại hai điểm M và N.
   

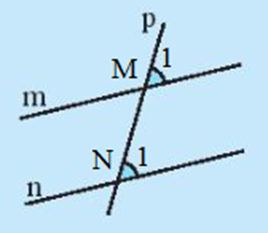
   Ta có: ${\widehat{M}}_1={\widehat{N}}_1$.
   Dự đoán: Đường thẳng m song song với n.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

3. Tìm các cặp đường thẳng song song trong Hình 5 và giải thích.
   
   

   Câu hỏi:
   

   Tìm các cặp đường thẳng song song trong Hình 5 và giải thích.
   

   Trả lời:

   – Hình 5a: Giả sử đường thẳng a, b với đường thẳng c lần lượt tại hai điểm A và B.
   

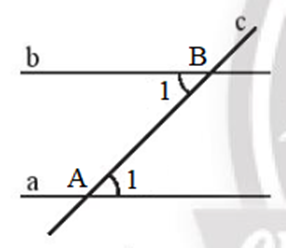
   Ta có: ${\widehat{A}}_1={\widehat{B}}_1={45}^o$ .
   Mà ${\widehat{A}}_1$  và ${\widehat{B}}_1$ ở vị trí so le trong.
   Do đó: a // b.
   – Hình 5b: Giả sử đường thẳng d, e với đường thẳng f lần lượt tại hai điểm D và E.
   

   Ta có: ${\widehat{D}}_1={90}^o;{\widehat{E}}_1={80}^o$ nên ${\widehat{D}}_1\ne {\widehat{E}}_1$ .
   Hai góc ${\widehat{D}}_1$ và ${\widehat{E}}_1$  ở vị trí so le trong.
   Do đó: đường thẳng d không song song với đường thẳng e.
   – Hình 3c: Giả sử đường thẳng m, n với đường thẳng p lần lượt tại hai điểm M và N.
   

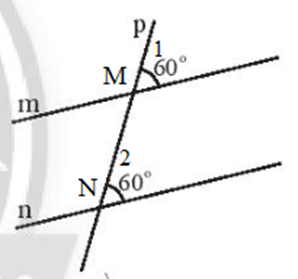
   Ta có: ${\widehat{M}}_1={\widehat{N}}_1={60}^o$ .
   Mà ${\widehat{M}}_1$ và ${\widehat{N}}_1$ ở vị trí đồng vị.
   Do đó: m // n.
   Vậy các cặp đường thẳng song song trong Hình 5 là: a // b, m // n.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

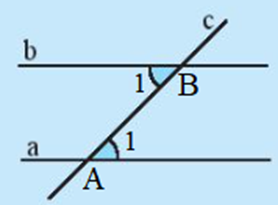
4. Cho hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c tại A và B (Hình 6). Hãy chứng tỏ a // b.
   
   

   Câu hỏi:
   

   Cho hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c tại A và B (Hình 6). Hãy chứng tỏ a // b.
   

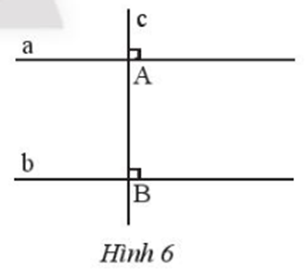
   Trả lời:

   

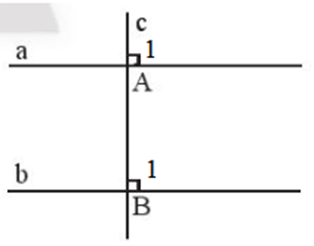
   Hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c tại A và B hay $a\perp c$ tại A và $b\perp c$ tại B.
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

5. a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua đỉnh A và song song với BC, cách vẽ đường thẳng b đi qua đỉnh B và song song với AC. b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?
   
   

   Câu hỏi:
   

   a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua đỉnh A và song song với BC, cách vẽ đường thẳng b đi qua đỉnh B và song song với AC.
   b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?

   Trả lời:

   a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua đỉnh A và song song với BC, cách vẽ đường thẳng b đi qua đỉnh B và song song với AC.
   Cách vẽ:
   – Vẽ tam giác ABC bất kì.
   – Đo số đo của $\widehat{ACB}$.
   – Vẽ đường thẳng a đi qua điểm A sao cho $\widehat{CAa}=\widehat{ACB}$.
   Khi đó, ta có đường thẳng a đi qua đỉnh A và song song với BC.
   – Vẽ đường thẳng b đi qua điểm B sao cho $\widehat{CBb}=\widehat{ACB}$.
   Khi đó, ta có đường thẳng b đi qua đỉnh B và song song với AC.
   Ta có hình vẽ:
   

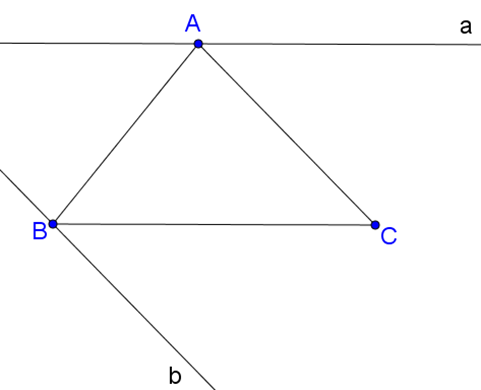
   b) Theo tiên đề Ơ-clit về đường thẳng song song thì qua một điểm ta chỉ vẽ được một đường thẳng a song song với đường thẳng BC, một đường thẳng b song song với đường thẳng AC.
   Vậy có thể vẽ được một đường thẳng a và một đường thẳng b.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====