Cho hình vẽ Biết a⊥AB, b⊥AB, M1^=60o. Tính N2^

Câu hỏi:

Cho hình vẽ Biết $a\perp AB, b\perp AB,$ $\widehat{M_1}={60}^o$. Tính $\widehat{N_2}$

A. 120$°$

Đáp án chính xác

B. 100$°$

C. 60$°$

D. 80$°$

Trả lời:

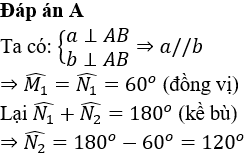
====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Chọn câu đúng. Hai góc đối đỉnh là:
   
   

   Câu hỏi:
   

   Chọn câu đúng. Hai góc đối đỉnh là:

   A. Hai góc có tổng số đo bằng 90$°$

   B. Hai góc có chung 1 cạnh

   C. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

   Đáp án chính xác

   D. Hai góc có tổng số đo bằng 360$°$

   Trả lời:

   Đáp án CHai góc đối đỉnh là hai góc mà mỗi cạnh góc này là tia đối của một cạnh của góc kia.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

2. Hình vẽ sau có bao nhiêu cặp góc so le trong
   
   

   Câu hỏi:
   

   Hình vẽ sau có bao nhiêu cặp góc so le trong

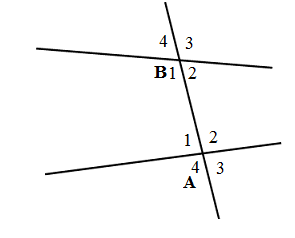
   A. 3

   B. 5

   C. 2

   Đáp án chính xác

   D. 4

   Trả lời:

   

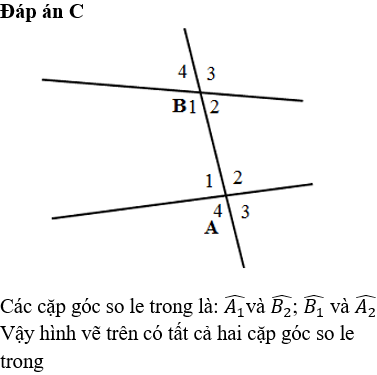
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

3. Em hãy chọn phát biểu đúng trong các phát biểu sau:Một đường thẳng cắt hai đường thẳng phân biệt thì tạo thành
   
   

   Câu hỏi:
   

   Em hãy chọn phát biểu đúng trong các phát biểu sau:Một đường thẳng cắt hai đường thẳng phân biệt thì tạo thành

   A. Hai góc so le trong bằng nhau

   B. Hai góc đồng vị bằng nhau

   C. Hai góc đối đỉnh bằng nhau

   Đáp án chính xác

   D. Hai góc so le ngoài bằng nhau

   Trả lời:

   Đáp án C+ Các đáp án A, B, D sai vì phải thêm điều kiện song song : “Một đường thẳng cắt hai đường thẳng song song thì tạo ra các cặp góc so le trong, so le ngoài, đồng vị bằng nhau.”+ Đáp án C đúng vì hai đường thẳng cắt nhau luôn tạo ra hai cặp góc đối đỉnh bằng nhau.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

4. Cho ba đường thẳng phân biệt a,b,c. Biết a⊥c, b⊥c, ta suy ra:
   
   

   Câu hỏi:
   

   Cho ba đường thẳng phân biệt a,b,c. Biết $a\perp c, b\perp c,$ ta suy ra:

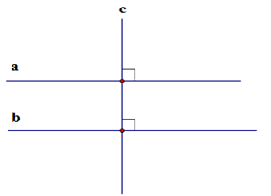
   A. a//b

   Đáp án chính xác

   B. a cắt b

   C. a $\perp$ b

   D. Cả A,B,C đều sai

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

5. Cho hình vẽ sau Hai góc BAC^ và ACD^ là hai góc nằm ở vị trí nào?
   
   

   Câu hỏi:
   

   Cho hình vẽ sau Hai góc $\widehat{BAC}$ và $\widehat{ACD}$ là hai góc nằm ở vị trí nào?

   A. So le trong

   B. Đồng vị

   C. Trong cùng phía

   Đáp án chính xác

   D. Đối đỉnh

   Trả lời:

   Đáp án CHai góc $\widehat{BAC}$ và $\widehat{ACD}$ là hai góc trong cùng phía

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====