Cho hình vẽ sau và cho biết tia OC là tia phân giác của góc nào?  

Câu hỏi:

Cho hình vẽ sau và cho biết tia OC là tia phân giác của góc nào?
 

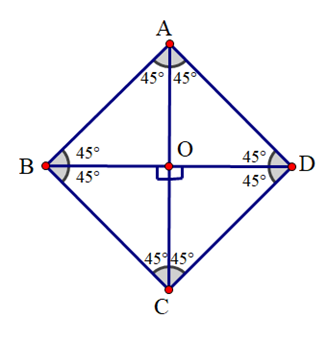
A. \(\widehat {BAD}\);

B. \(\widehat {BOD}\);

Đáp án chính xác

C. \(\widehat {BCD}\);

D. \(\widehat {ABC}\).

Trả lời:

Hướng dẫn giải:
Đáp án đúng là: B
Ta có tia OC nằm giữa hai tia OB và OD nên:
\(\widehat {BOC} = \widehat {COD} = {90^o}\) (do \(\widehat {BOC};\widehat {COD}\) là hai góc vuông)
Do đó OC là tia phân giác của \(\widehat {BOD}\).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

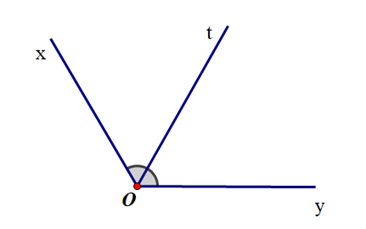
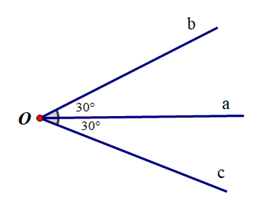
1. Quan sát hình vẽ sau và cho biết tia Ob có là tia phân giác của \(\widehat {aOc}\) không? Vì sao?
   
   

   Câu hỏi:
   

   Quan sát hình vẽ sau và cho biết tia Ob có là tia phân giác của \(\widehat {aOc}\) không? Vì sao?
   

   Trả lời:

   Hướng dẫn giải:
   Từ hình vẽ trên, ta thấy:
   + Tia Ob nằm giữa hai tia Oa, Oc.
   + \(\widehat {aOb} = \widehat {bOc}\) (vì cùng bằng 30^o).
   Vậy Ob là tia phân giác của \(\widehat {aOc}\).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

2. Cho \(\widehat {xOy} = {120^o}\). Vẽ tia Ot là phân giác \(\widehat {xOy}\) bằng các cách sau đây: Thước đo góc;
   
   

   Câu hỏi:
   

   Cho \(\widehat {xOy} = {120^o}\). Vẽ tia Ot là phân giác \(\widehat {xOy}\) bằng các cách sau đây:
   Thước đo góc;

   Trả lời:

   Hướng dẫn giải:
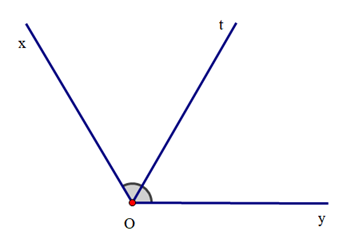
   Vẽ tia Ot là phân giác \(\widehat {xOy}\) bằng thước đo góc:
   + Đặt tâm của thước đo góc trùng với đỉnh của góc sao cho một cạnh của thước đo trùng với một cạnh của góc:
   
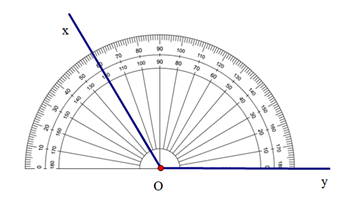
   + Tính \(\frac{{\widehat {xOy}}}{2} = \frac{{{{120}^o}}}{2} = {60^o}\).
   + Đánh dấu điểm chỉ vạch 60°:
   
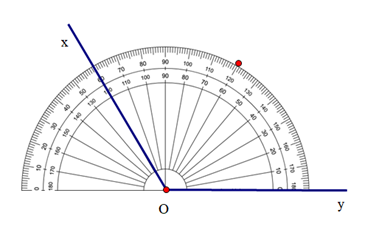
   + Dùng thước nối từ đỉnh của góc tới điểm đã đánh dấu ta được tia phân giác.
   
   

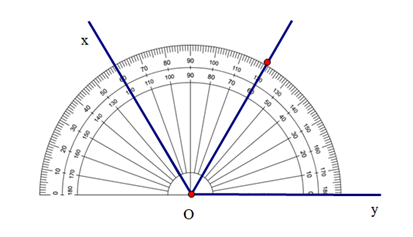
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

3. Cho \(\widehat {xOy} = {120^o}\). Vẽ tia Ot là phân giác \(\widehat {xOy}\) bằng các cách sau đây: Thước hai lề;
   
   

   Câu hỏi:
   

   Cho \(\widehat {xOy} = {120^o}\). Vẽ tia Ot là phân giác \(\widehat {xOy}\) bằng các cách sau đây:
   Thước hai lề;

   Trả lời:

   Hướng dẫn giải:

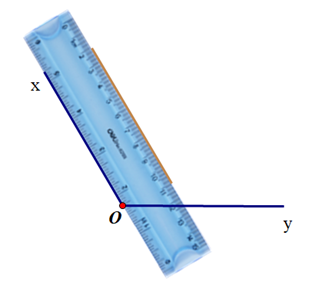
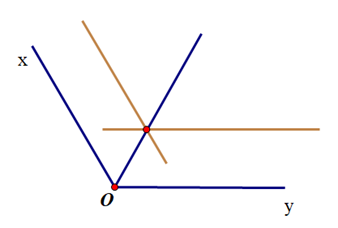
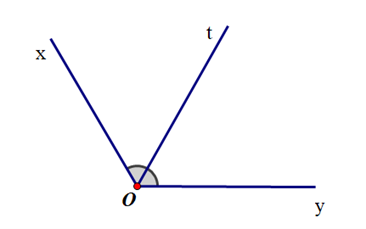
   Vẽ tia Ot là phân giác \(\widehat {xOy}\) bằng thước hai lề:
   + Đặt 1 lề thước thẳng trùng với cạnh Ox (sao cho thước thẳng nằm phía trong \(\widehat {xOy}\)), rồi dùng bút chì kẻ theo lề còn lại của thước.
   
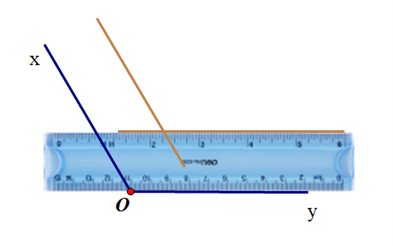
   + Thực hiện tương tự đặt 1 lề thước thẳng trùng với cạnh Oy, rồi dùng bút chì kẻ theo lề còn lại của thước.
   
   + Đánh dấu giao điểm của hai đường thẳng vừa kẻ.
   
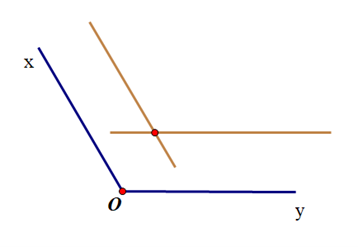
   + Dùng thước nối từ đỉnh của góc tới điểm đã đánh dấu ta được tia phân giác.
   
    
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

4. Cho \(\widehat {xOy} = {120^o}\). Vẽ tia Ot là phân giác \(\widehat {xOy}\) bằng các cách sau đây: Compa.
   
   

   Câu hỏi:
   

   Cho \(\widehat {xOy} = {120^o}\). Vẽ tia Ot là phân giác \(\widehat {xOy}\) bằng các cách sau đây:
   Compa.

   Trả lời:

   Hướng dẫn giải:

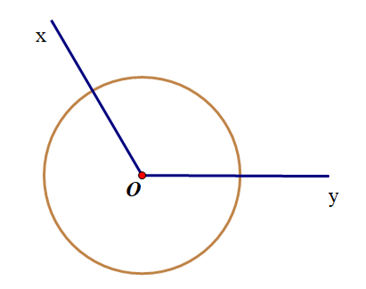
   Vẽ tia Ot là phân giác \(\widehat {xOy}\) bằng compa
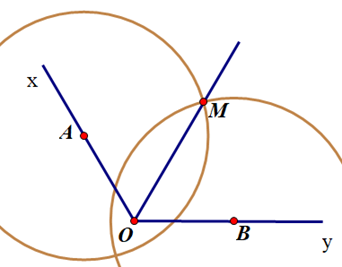
   + Dựng đường tròn tâm O và bán kính tuỳ ý.
   
   + Đánh dấu giao điểm của đường tròn vừa vẽ với hai cạnh Ox, Oy.
   
   
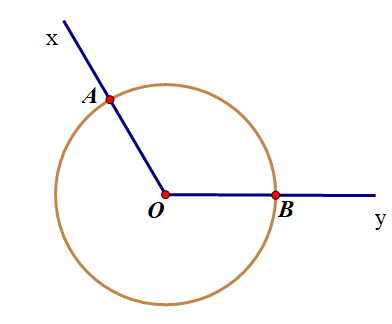
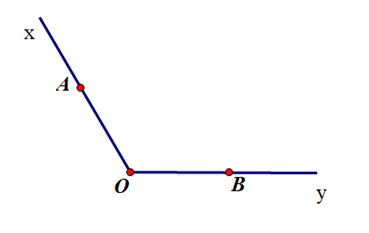
   + Dựng cung tròn tâm A và cung tròn tâm B có cùng bán kính sao cho hai cung tròn này cắt nhau tại điểm M nằm trong \(\widehat {xOy}\).
   
   + Dùng thước nối từ đỉnh O tới điểm M được tia phân giác.
   
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

5. Tia Ob là phân giác của \(\widehat {aOc}\) trong hình vẽ nào dưới đây?
   
   

   Câu hỏi:
   

   Tia Ob là phân giác của \(\widehat {aOc}\) trong hình vẽ nào dưới đây?

   A.
   ;

   B.
   ;

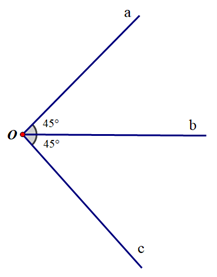   Đáp án chính xác

   C.
   ;

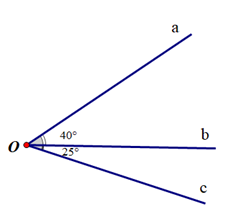   D.
   .

   Trả lời:

   Hướng dẫn giải:
   Đáp án đúng là: B
   Đáp án A: Tia Ob không nằm giữa hai tia Oa và Oc nên Ob không là tia phân giác của \(\widehat {aOc}\).
   Đáp án B: Tia Ob nằm giữa hai tia Oa và Oc; \(\widehat {aOb} = \widehat {bOc}\) (cùng bằng 45°). Do đó Ob là tia phân giác của \(\widehat {aOc}\).
   Đáp án C: Tia Ob nằm giữa hai tia Oa và Oc; \(\widehat {aOb} \ne \widehat {bOc}\) (do 40° ≠ 25°) nên Ob không là tia phân giác của \(\widehat {aOc}\).
   Đáp án D: Tia Ob không nằm giữa hai tia Oa và Oc nên Ob không là tia phân giác của \(\widehat {aOc}\).
   Như vậy tia Ob là phân giác của \(\widehat {aOc}\) trong hình vẽ ở đáp án B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====