Cho tấm bìa bên dưới. Sau khi gấp tấm bìa theo đường gấp khúc, ta tạo lập được hình lăng trụ đứng nào dưới đây?

Câu hỏi:

Cho tấm bìa bên dưới.

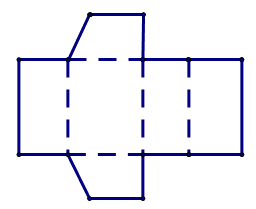
Sau khi gấp tấm bìa theo đường gấp khúc, ta tạo lập được hình lăng trụ đứng nào dưới đây?

A. 

B. 

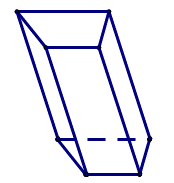
C.

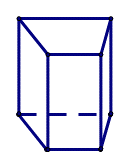
Đáp án chính xác

D. 

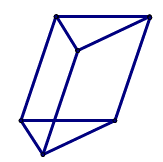
Trả lời:

Hướng dẫn giải:
Đáp án đúng là: C
Quan sát tấm bìa, ta thấy hình lăng trụ đứng có đáy là tứ giác (cụ thể trong bài này là hình thang).
Hình lăng trụ ở đáp án A, D có đáy là hình tam giác.
Do đó ta loại đáp án A, D.
Hình lăng trụ ở đáp án B có chiều cao không vuông góc với đáy.
Do đó hình lăng trụ ở đáp án B không phải là hình lăng trụ đứng.
Vì vậy ta loại đáp án B.
Vậy ta chọn đáp án C.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Hãy quan sát lăng trụ đứng tam giác (Hình 1) và thực hiện các yêu cầu sau: a) Tính tổng diện tích ba mặt bên của hình lăng trụ đứng. b) Gọi Cđáy là chu vi đáy và h là chiều cao của hình lăng trụ, tính Cđáy . h. c) So sánh kết quả của câu a và câu b.
   
   

   Câu hỏi:
   

   Hãy quan sát lăng trụ đứng tam giác (Hình 1) và thực hiện các yêu cầu sau:
   a) Tính tổng diện tích ba mặt bên của hình lăng trụ đứng.
   b) Gọi C_đáy là chu vi đáy và h là chiều cao của hình lăng trụ, tính C_đáy . h.
   c) So sánh kết quả của câu a và câu b.
   

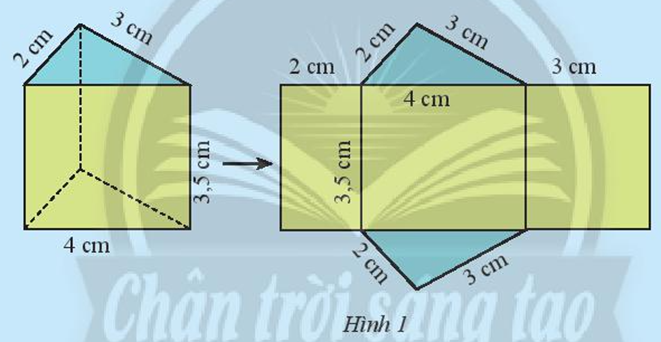
   Trả lời:

   a) Hình lăng trụ đứng có ba mặt bên đều là hình chữ nhật:
   – Mặt bên thứ nhất có dạng hình chữ nhật có chiều dài 3,5 cm và chiều rộng 2 cm nên có diện tích là:
   3,5 . 2 = 7 (cm²).
   – Mặt bên thứ hai có dạng hình chữ nhật có chiều dài 4 cm và chiều rộng 3,5 cm nên có diện tích là:
   4 . 3,5 = 14 (cm²).
   – Mặt bên thứ ba có dạng hình chữ nhật có chiều dài 3,5 cm và chiều rộng 3 cm nên có diện tích là:
   3,5 . 3 = 10,5 (cm²).
   Tổng diện tích ba mặt bên của hình lăng trụ đứng là:
   7 + 14 + 10,5 = 31,5 (cm²).
   Vậy tổng diện tích ba mặt bên của hình lăng trụ đứng là 31,5 cm².
   b) Chu vi đáy của hình lăng trụ đứng là:
   C_đáy = 2 + 3 + 4 = 9 (cm).
   Vậy C_đáy . h = 9 . 3,5 = 31,5 (cm²).
   c) Kết quả thu được ở câu a và câu b đều bằng nhau.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

2. Tính diện tích xung quanh của lăng trụ đứng có đáy là hình thang được cho trong Hình 2.
   
   

   Câu hỏi:
   

   Tính diện tích xung quanh của lăng trụ đứng có đáy là hình thang được cho trong Hình 2.
   

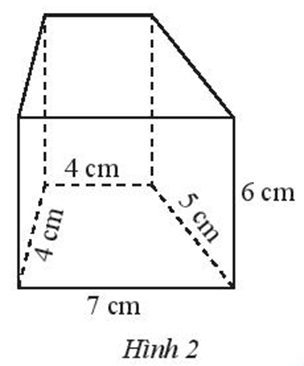
   Trả lời:

   Hình lăng trụ đứng có đáy là hình thang được cho trong Hình 2 có chiều cao là 6 cm.
   Chu vi đáy của lăng trụ đứng là:
   4 + 4 + 5 + 7 = 20 (cm).
   Diện tích xung quanh của lăng trụ đứng là:
   20 . 6 = 120 (cm²).
   Vậy diện tích xung quanh của lăng trụ đứng trong Hình 2 là 120 cm².

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

3. Cho hình hộp chữ nhật với kích thước như Hình 3a. Hình hộp này được cắt đi một nửa để có hình lăng trụ đứng như Hình 3b. a) Tính thể tích của hình hộp chữ nhật. b) Dự đoán thể tích của hình lăng trụ đứng tam giác dựa vào thể tích hình hộp chữ nhật ở câu a. c) Gọi Sđáy là diện tích mặt đáy và h là chiều cao của hình lăng trụ đứng tam giác. Hãy tính Sđáy . h. d) So sánh Sđáy . h và kết quả dự đoán ở câu b.
   
   

   Câu hỏi:
   

   Cho hình hộp chữ nhật với kích thước như Hình 3a. Hình hộp này được cắt đi một nửa để có hình lăng trụ đứng như Hình 3b.
   

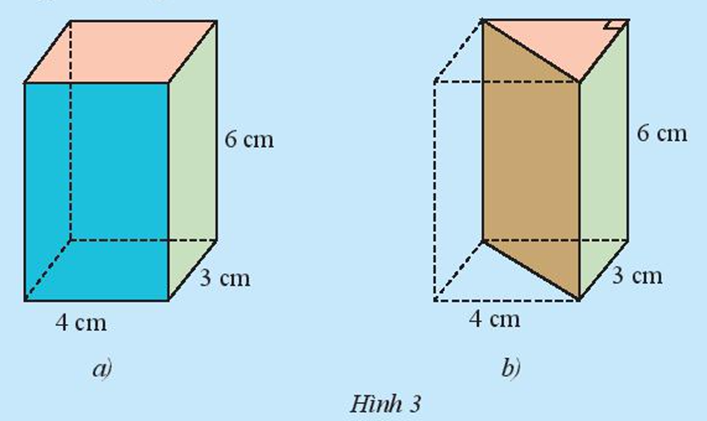
   a) Tính thể tích của hình hộp chữ nhật.
   b) Dự đoán thể tích của hình lăng trụ đứng tam giác dựa vào thể tích hình hộp chữ nhật ở câu a.
   c) Gọi S_đáy là diện tích mặt đáy và h là chiều cao của hình lăng trụ đứng tam giác. Hãy tính S_đáy . h.
   d) So sánh S_đáy . h và kết quả dự đoán ở câu b.

   Trả lời:

   a) Thể tích của hình hộp chữ nhật là:
   4 . 3 . 6 = 72 (cm³)
   b) Dự đoán: Thể tích của hình lăng trụ đứng tam giác bằng một nửa thể tích hình hộp chữ nhật.
   c) Diện tích đáy của hình lăng trụ đứng tam giác là:
   $\frac{1}{2}.3.4=6$ (cm²)
   Vậy S_đáy . h = 6 . 6 = 36 (cm³).
   d) Kết quả dự đoán ở câu b là đúng.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

4. Tính diện tích xung quanh của một trụ bê tông hình lăng trụ đứng có chiều cao 2 m và đáy là tam giác đều có cạnh 0,5 m (Hình 4).
   
   

   Câu hỏi:
   

   Tính diện tích xung quanh của một trụ bê tông hình lăng trụ đứng có chiều cao 2 m và đáy là tam giác đều có cạnh 0,5 m (Hình 4).
   

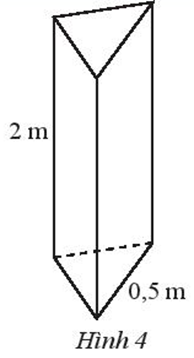
   Trả lời:

   Chu vi đáy của một trụ bê tông hình lăng trụ đứng là:
   0,5 . 3 = 1,5 (m)
   Diện tích xung quanh của một trụ bê tông hình lăng trụ đứng là:
   1,5 . 2 = 3 (m²)
   Vậy diện tích xung quanh của một trụ bê tông hình lăng trụ đứng là 3 m².

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   

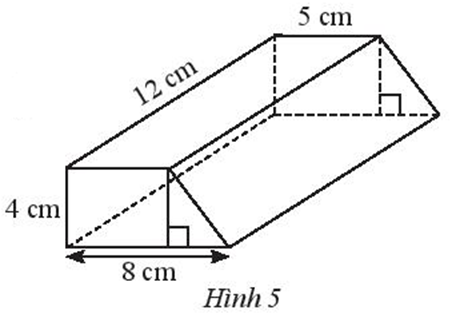
5. Tính thể tích lăng trụ đứng tứ giác có đáy là hình thang với kích thước cho trong Hình 5.
   
   

   Câu hỏi:
   

   Tính thể tích lăng trụ đứng tứ giác có đáy là hình thang với kích thước cho trong Hình 5.
   

   Trả lời:

   Diện tích đáy của lăng trụ đứng tứ giác là:
   $\frac{5+8}{2}.4=26$ (cm²)
   Thể tích lăng trụ đứng tứ giác là:
   26 . 12 = 312 (cm³)
   Vậy thể tích lăng trụ đứng tứ giác có đáy là hình thang là 312 cm³.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====