Câu hỏi:
Cho \(\widehat {xOy}\) khác góc bẹt. Trên tia phân giác Ot của \(\widehat {xOy}\), lấy điểm I (I ≠ O). Gọi A, B lần lượt là các điểm trên các tia Ox, Oy sao cho OA = OB (O ≠ A và O ≠ B). Kết luận nào sau đây đúng nhất?
A.Ot vuông góc với AB;
B.Ot là đường trung trực của đoạn thẳng AB;
Đáp án chính xác
C. Ot đi qua trung điểm của AB;
D. \(\widehat {OAI} \ne \widehat {OBI}\).
Trả lời:
Đáp án đúng là: B

Xét ∆OAI và ∆OBI, có:
OI là cạnh chung.
OA = OB (giả thiết).
\(\widehat {AOI} = \widehat {BOI}\) (OI là phân giác của \(\widehat {AOB}\)).
Do đó ∆OAI = ∆OBI (cạnh – góc – cạnh).
Suy ra AI = BI và \(\widehat {OAI} = \widehat {OBI}\) (cặp cạnh và cặp góc tương ứng).
Vì \(\widehat {OAI} = \widehat {OBI}\) nên đáp án D sai.
Vì AI = BI (chứng minh trên) và OA = OB (giả thiết).
Nên OI là đường trung trực của đoạn thẳng AB.
Hay Ot là đường trung trực của đoạn thẳng AB.
Do đó đáp án B đúng nhất.
Vậy ta chọn đáp án B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đường thẳng d trong hình vẽ nào sau đây là đường trung trực của đoạn thẳng MN?
Câu hỏi:
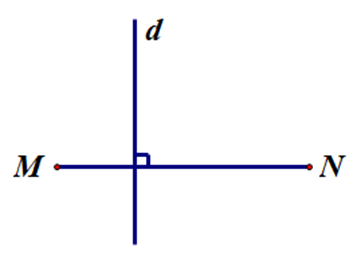
Đường thẳng d trong hình vẽ nào sau đây là đường trung trực của đoạn thẳng MN?
A.

Đáp án chính xác
B.

C.
D.

Trả lời:
Đáp án đúng là: A
Một đường thẳng là đường trung trực của một đoạn thẳng khi thỏa mãn cả hai yếu tố sau:
+ Đi qua trung điểm của đoạn thẳng.
+ Vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.
– Đường thẳng d ở đáp án A có đi qua trung điểm I của đoạn thẳng AB và vuông góc với đoạn thẳng MN tại trung điểm I.
Do đó đường thẳng d ở đáp án A là đường trung trực của đoạn thẳng MN.
– Đường thẳng d ở đáp án B, D có đi qua trung điểm I nhưng không vuông góc với đoạn thẳng MN tại trung điểm I.
Do đó đường thẳng d ở đáp án B, D không là đường trung trực của đoạn thẳng MN.
– Đường thẳng d ở đáp án C không đi qua trung điểm của đoạn thẳng MN.
Do đó đường thẳng d ở đáp án C không là đường trung trực của đoạn thẳng MN.
Vậy ta chọn đáp án A.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ∆ABC có AB < AC, đường phân giác AD. Trên cạnh AC, lấy điểm E sao cho AE = AB. Kết luận nào sau đây đúng nhất?
Câu hỏi:
Cho ∆ABC có AB < AC, đường phân giác AD. Trên cạnh AC, lấy điểm E sao cho AE = AB. Kết luận nào sau đây đúng nhất?
A. AD vuông góc với BC;
B. AD vuông góc với BE;
C. AD là đường trung trực của đoạn thẳng BE;
Đáp án chính xác
D. AD đi qua trung điểm của đoạn thẳng BE.
Trả lời:
Đáp án đúng là: C

Xét ∆ABD và ∆AED, có:
AD là cạnh chung.
\(\widehat {BAD} = \widehat {EAD}\) (AD là phân giác của \(\widehat {BAC}\)).
AB = AE (giả thiết).
Do đó ∆ABD = ∆AED (cạnh – góc – cạnh).
Suy ra BD = ED.
Mà AB = AE (giả thiết).
Do đó AD là đường trung trực của đoạn thẳng BE.
Vì AD là đường trung trực của đoạn thẳng BE nên AD vừa vuông góc với BE, vừa đi qua trung điểm của đoạn thẳng BE.
Do đó đáp án C đúng nhất.
Với E ∈ AC, ta có AB = AE (giả thiết) và AB < AC (giả thiết).
Do đó AE < AC.
Suy ra ba điểm B, E, C không thẳng hàng.
Mà AD vuông góc với BE.
Nên AD không vuông góc với BC.
Do đó đáp án A sai.
Vậy ta chọn đáp án C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ∆ABC cân tại A. Gọi M là một điểm nằm trong tam giác sao cho MB = MC, N là trung điểm của BC. Khẳng định nào sau đây đúng nhất?
Câu hỏi:
Cho ∆ABC cân tại A. Gọi M là một điểm nằm trong tam giác sao cho MB = MC, N là trung điểm của BC. Khẳng định nào sau đây đúng nhất?
A. AM là đường trung trực của đoạn thẳng BC;
B. AN là đường trung trực của đoạn thẳng BC;
C. MN là đường trung trực của đoạn thẳng BC;
D. Cả A, B, C đều đúng.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D

Gọi d là đường trung trực của đoạn thẳng BC.
Vì AB = AC (∆ABC cân tại A).
Nên A cách đều hai điểm B, C.
Do đó A thuộc đường trung trực của đoạn thẳng BC hay A ∈ d (1).
Vì MB = MC (giả thiết).
Nên M cách đều hai điểm B, C.
Do đó M thuộc đường trung trực của đoạn thẳng BC hay M ∈ d (2).
Vì N là trung điểm BC (giả thiết).
Nên N ∈ d (3).
Từ (1), (2), ta có thể nói AM là đường trung trực của đoạn thẳng BC.
Do đó đáp án A đúng.
Từ (1), (3), ta có thể nói AN là đường trung trực của đoạn thẳng BC.
Do đó đáp án B đúng.
Từ (2), (3), ta có thể nói MN là đường trung trực của đoạn thẳng BC.
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ∆ABC có AB < AC. Lấy E ∈ AC sao cho AE = AB. Trên tia đối của tia BA lấy điểm D sao cho BD = EC. Kẻ AH ⊥ BE tại H, AH cắt DC tại K. Chọn khẳng định đúng.
Câu hỏi:
Cho ∆ABC có AB < AC. Lấy E ∈ AC sao cho AE = AB. Trên tia đối của tia BA lấy điểm D sao cho BD = EC. Kẻ AH ⊥ BE tại H, AH cắt DC tại K. Chọn khẳng định đúng.
A. \(\widehat {ADC} = \widehat {ACD}\);
B. AK ⊥ DC;
C. AK là đường trung trực của đoạn thẳng DC;
D. Cả A, B, C đều đúng.
Đáp án chính xác
Trả lời:
Đáp án đúng là: D

Vì AB = AE (giả thiết).
Nên ∆ABE cân tại A.
Suy ra \(\widehat {ABE} = \widehat {AEB}\).
∆ABE có: \(\widehat {BAC} + \widehat {ABE} + \widehat {AEB} = 180^\circ \).
Suy ra \(2\widehat {ABE} = 180^\circ – \widehat {BAC}\) (1).
Vì ba điểm A, B, D thẳng hàng và B nằm giữa A, D nên AD = AB + BD.
Vì ba điểm A, E, C thẳng hàng và E nằm giữa A, C nên AC = AE + EC.
Mà AB = AE và BD = EC (giả thiết).
Do đó AD = AC.
Suy ra ∆ADC cân tại A.
Khi đó ta có \(\widehat {ADC} = \widehat {ACD}\).
Do đó đáp án A đúng.
∆ADC có: \(\widehat {BAC} + \widehat {ADC} + \widehat {ACD} = 180^\circ \).
Suy ra \(2\widehat {ADC} = 180^\circ – \widehat {BAC}\) (2).
Từ (1), (2), ta suy ra \(\widehat {ADC} = \widehat {ABE}\).
Mà hai góc này ở vị trí đồng vị.
Do đó BE // DC.
Lại có AH ⊥ BE (giả thiết).
Suy ra AH ⊥ DC hay AK ⊥ DC (*).
Do đó đáp án B đúng.
Xét ∆ADK và ∆ACK, có:
AK là cạnh chung.
AD = AC (chứng minh trên).
\(\widehat {AKD} = \widehat {AKC} = 90^\circ \) (chứng minh trên).
Do đó ∆ADK = ∆ACK (cạnh huyền – cạnh góc vuông).
Suy ra DK = CK (cặp cạnh tương ứng).
Do đó K là trung điểm DC (**).
Từ (*), (**), ta suy ra AK là đường trung trực của đoạn thẳng DC.
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho ∆ABC cân tại A, đường phân giác trong của \(\widehat A\) cắt BC tại D. Khẳng định nào dưới đây sai?
Câu hỏi:
Cho ∆ABC cân tại A, đường phân giác trong của \(\widehat A\) cắt BC tại D. Khẳng định nào dưới đây sai?
A. AD là đường trung trực của BC;
B. \(\widehat {ABC} + \widehat {CAD} = 90^\circ \);
C. ∆ADB = ∆ADC;
D. \(\widehat {ABC} + \widehat {ADC} = 180^\circ \).
Đáp án chính xác
Trả lời:
Đáp án đúng là: D

Xét ∆ABD và ∆ACD, có:
AD là cạnh chung.
\(\widehat {BAD} = \widehat {CAD}\) (AD là phân giác của \(\widehat {BAC}\)).
AB = AC (∆ABC cân tại A).
Do đó ∆ABD = ∆ACD (cạnh – góc – cạnh).
Suy ra đáp án C đúng.
Ta có ∆ABD = ∆ACD (chứng minh trên).
Suy ra BD = CD và \(\widehat {ADB} = \widehat {ADC}\) (cặp cạnh và cặp góc tương ứng).
Vì BD = CD nên D là trung điểm BC (1).
Ta có \(\widehat {ADB} + \widehat {ADC} = 180^\circ \) (hai góc kề bù).
Suy ra \(2\widehat {ADC} = 180^\circ \).
Do đó \(\widehat {ADB} = \widehat {ADC} = 90^\circ \).
Suy ra AD ⊥ BC (2).
Từ (1), (2), ta suy ra AD là đường trung trực của BC.
Do đó đáp án A đúng.
∆ABD vuông tại D: \(\widehat {ABD} + \widehat {BAD} = 90^\circ \).
Suy ra \(\widehat {ABC} + \widehat {CAD} = 90^\circ \) (Vì AD là phân giác của \(\widehat {BAC}\) nên \(\widehat {BAD} = \widehat {CAD}\)).
Do đó đáp án B đúng.
∆ABD vuông tại D: \(\widehat {ABD} + \widehat {BAD} = 90^\circ \).
Suy ra \(\widehat {ABC} < 90^\circ \).
Mà \(\widehat {ADC} = 90^\circ \) (theo (2)).
Do đó \(\widehat {ABC} + \widehat {ADC} < 90^\circ + 90^\circ = 180^\circ \).
Khi đó ta có \(\widehat {ABC} + \widehat {ADC} < 180^\circ \).
Do đó đáp án D sai.
Vậy ta chọn đáp án D.====== **** mời các bạn xem câu tiếp bên dưới **** =====