Câu hỏi:
Hình thức đánh giá: theo hình thức đánh giá của học sinh dự án.
Trả lời:
1. Đánh giá hoạt động cá nhân
– Mỗi cá nhân tự đánh giá vào phiếu cá nhân.
– Nhóm đánh giá từng thành viên trong nhóm vào phiếu đánh giá cá nhân.
2. Đánh giá hoạt động và sản phẩm của nhóm
– Nhóm tự đánh giá lại hoạt động của nhóm và cho vào phiếu đánh giá hoạt động của nhóm.
– Giáo viên và các nhóm đánh giá, rồi cho điểm phần trình bày của từng nhóm vào phiếu đánh giá hoạt động nhóm.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- I. Nội dung chính của chủ đề
Câu hỏi:
I. Nội dung chính của chủ đề
Trả lời:
1. Giới thiệu về khuyến mãi trong kinh doanh (sgk)
2. Hình thức giảm giá trong khuyến mãi
3. Kiến thức toán học
– Sau khi giảm x% số a, ta nhân được số a.(100% – x%)
– Sau khi tăng x% số a, ta nhận được số a.(100% + x%).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Giáo viên thực hiện những nhiệm vụ sau
Câu hỏi:
Giáo viên thực hiện những nhiệm vụ sau
Trả lời:
– Quy định hệ thống đơn vị tiền giả định, chẳng hạn gồm: 1 000 đồng giả định, 2 000 đồng giả định, 5 000 đồng giả định, 10 000 đồng giả định, 20 000 đồng giả định; 50 000 đồng giả định.
– Giáo viên chuẩn bị 600 000 đồng đến 700 000 đồng giả định;
– Quy định danh mục sản phẩm (nên tối đa 5 loại sản phẩm) và giá nhập vào mỗi loại sản phẩm, số lượng sản phẩn cần đủ nhiều sao cho tổng số tiền thu được số sản phẩm đó (theo giá quy định) tối thiểu là 400 000 đồng giả định;
– Chia lớp thành 4 nhóm học sinh và cử nhóm trưởng của mỗi nhóm;
– Giao cho mỗi nhóm học sinh 20 sản phẩm, nhóm học sinh được quyền lựa sản phẩm trong danh mục sản phẩm đã quy định (mặt hàng cần kinh doanh) từ giáo viên theo đúng kế hoạch kinh doanh mà nhóm đã vạch ra sao cho tổng giá trị của 20 sản phẩm đó (tính theo giá nhập vào của từng loại sản phẩm) không vượt quá 100 000 đồng giả định.
– Mỗi nhóm được nhận 150 000 đồng giả định để thực hiện nhiệm vụ mua sản phẩm (mặt hàng kinh doanh) của nhóm khác, tuyệt đối không được mua sản phẩm kinh doanh của chính nhóm mình.
– Quy định rằng sản phẩm tồn lại khi trò chơi kết thúc được định giá bằng 50% giá ban đầu.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Học sinh được chia theo nhóm. Các nhóm trao đổi thảo luận.
Câu hỏi:
Học sinh được chia theo nhóm. Các nhóm trao đổi thảo luận.
Trả lời:
– Xác định rõ nhiệm vụ của nhóm và từng nhiệm vụ thành phần.
– Phân công nhiệm vụ cho các thành viên trong nhóm.
– Xác định thời gian hoàn thành từng nhiệm vụ thành phần và và nhiệm vụ chung.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Mỗi học sinh tiến hành lập kế hoạch kinh doanh của nhóm, đặc biệt lựa chọn hình thức khuyến mãi phù hợp để tăng lãi của nhóm.
Câu hỏi:
Mỗi học sinh tiến hành lập kế hoạch kinh doanh của nhóm, đặc biệt lựa chọn hình thức khuyến mãi phù hợp để tăng lãi của nhóm.
Trả lời:
a) Nhiệm vụ 1: Lập kế hoạch kinh doanh của mỗi nhóm
Thống nhất các công việc sau đây:
– Lựa chọn 20 sản phẩm (mặt hàng cần kinh doanh) sao cho tổng giá trị của 20 sản phẩm đó (tính theo giá nhập vào của từng loại sản phẩm) không vượt quá 100 000 đồng giả định;
– Lựa chọn hình thức kinh doanh, thảo luận các chiến lược kinh doanh;
– Phân công công việc cho từng thành viên trong nhóm; từng cá nhân dự kiến cách làm của mình và cả nhóm cùng trao đổi góp ý.
b) Nhiệm vụ 2: Xác định hình thức khuyến mãi và cách thức quảng cáo, thông tin về sản phẩm.
Thống nhất các công việc cần làm sau đây:
– Xác định hình thức giảm giá;
– Đưa ra thêm những hình thức khuyến mãi (nếu có):
– Xác định cách thực hiện quảng cáo, thông tin về sản phẩm và hình thức khuyến mãi.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- 2. Phần thực hiện
Thực hiện công việc kinh doanh (thực hành bán hàng). Tính doanh thu và lãi.
– Yêu cầu mong muốn:
Câu hỏi:
2. Phần thực hiện
Thực hiện công việc kinh doanh (thực hành bán hàng). Tính doanh thu và lãi.– Yêu cầu mong muốn:
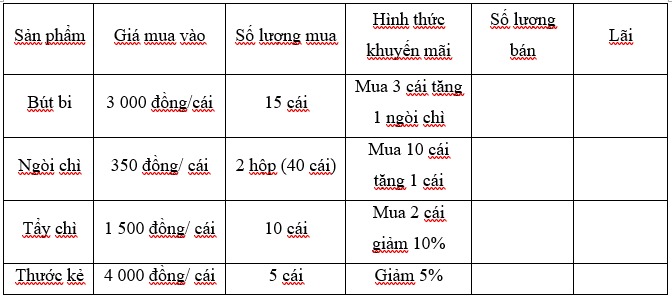
Trả lời:
– Kết quả đạt được:
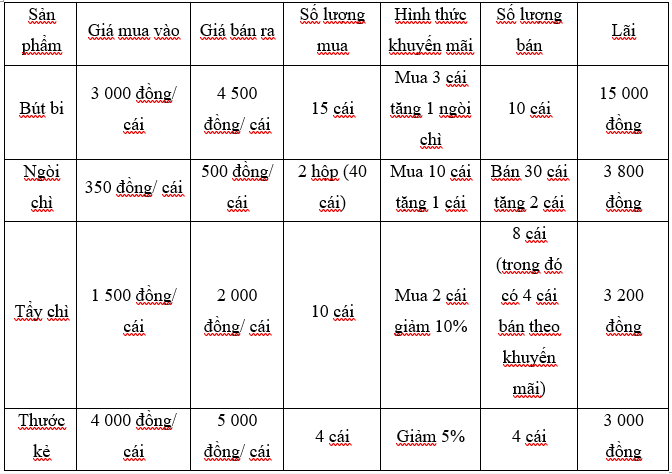
– Viết báo cáo kết quả:
(học sinh dựa vào bảng trên viết báo cáo kết quả)====== **** mời các bạn xem câu tiếp bên dưới **** =====