Câu hỏi:
Một chiếc bánh kem có dạng hình lập phương có cạnh 30 cm. Người ta cắt đi một miếng có dạng hình hộp chữ nhật với chiều dài 7 cm, chiều rộng 4 cm và chiều cao 6 cm. Thể tích phần còn lại của chiếc bánh kem là:
A. 168 cm3;
B. 27 000 cm3;
Đáp án chính xác
C. 26 832 cm3;
D. 27 168 cm3.
Trả lời:
Đáp án đúng là: BThể tích của chiếc bánh kem là:303 = 27 000 (cm3)Thể tích phần đã cắt là:7 . 4 . 6 = 168 (cm3)Thể tích phần còn lại của chiếc bánh kem là:27 000 – 168 = 26 832 (cm3)Do đó thể tích phần còn lại của chiếc bánh kem là 26 832 cm3.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Làm thế nào để tính được tổng diện tích các mặt và thể tích của khối gỗ ở hình bên?
Câu hỏi:
Làm thế nào để tính được tổng diện tích các mặt và thể tích của khối gỗ ở hình bên?
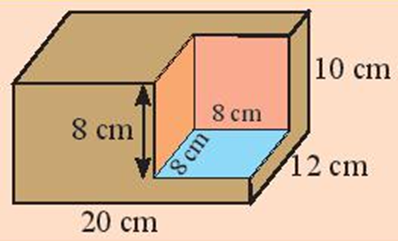
Trả lời:
Khối gỗ trên được tạo thành từ khối gỗ có dạng hình hộp chữ nhật có chiều dài 20 cm, chiều rộng 12 cm và chiều cao 10 cm.
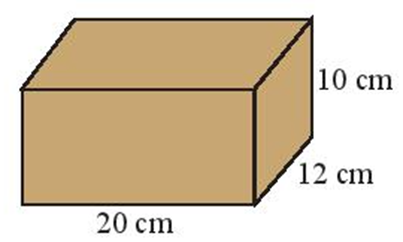
Sau đó, cắt bỏ một phần khối gỗ: phần cắt bỏ có dạng hình lập phương có cạnh là 8 cm. Ta được khối gỗ như hình sau:
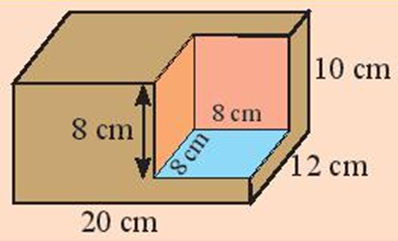
Do đó, diện tích các mặt của khối gỗ sau khi cắt sẽ bằng diện tích các mặt của khối gỗ hình hộp chữ nhật ban đầu.
Thể tích của khối gỗ sau khi cắt được tính bằng thể tích khối gỗ ban đầu (có dạng hình hộp chữ nhật) trừ khi thể tích khối gỗ đã bị cắt (có dạng hình lập phương).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Một khối bê tông, được đặt trên mặt đất, có kích thước như Hình 3.
a) Người ta muốn sơn tất cả các mặt của khối bê tông trừ mặt tiếp giáp với mặt đất. Hỏi chi phí để sơn là bao nhiêu? Biết rằng để sơn mỗi mét vuông tốn 25 nghìn đồng.
b) Tính thể tích của khối bê tông.
Câu hỏi:
Một khối bê tông, được đặt trên mặt đất, có kích thước như Hình 3.
a) Người ta muốn sơn tất cả các mặt của khối bê tông trừ mặt tiếp giáp với mặt đất. Hỏi chi phí để sơn là bao nhiêu? Biết rằng để sơn mỗi mét vuông tốn 25 nghìn đồng.
b) Tính thể tích của khối bê tông.
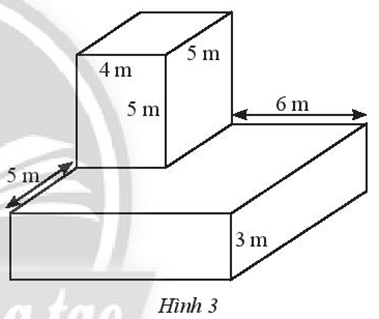
Trả lời:
a) Diện tích toàn phần của hình hộp chữ nhật bằng diện tích xung quanh cộng với diện tích 2 mặt đáy.
Stp = 2 . (a + b) . h + 2 . a . b.
(với a, b, h lần lượt là chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật).
Khối bê tông ở Hình 3 tạo bởi hai hình hộp chữ nhật ghép lại với nhau.
Hình hộp chữ nhật bên dưới có đáy là hình vuông có cạnh bằng:
5 + 5 = 6 + 4 = 10 (m).
Diện tích toàn phần của hình hộp chữ nhật bên dưới là:
2 . (10 + 10) . 3 + 2 . 10 . 10 = 320 (m2).
Diện tích toàn phần của hộp chữ nhật bên trên là:
2 . (5 + 4) . 5 + 2 . 5 . 4 = 130 (m2).
Tổng diện tích các mặt tiếp xúc bằng tổng diện tích mặt tiếp xúc với mặt đất và diện tích tiếp xúc giữa hai khối và bằng:
102 + 2 . 4 . 5 = 140 (m2).
Diện tích các mặt cần sơn của khối bê tông bằng tổng diện tích toàn phần của hai khối bê tông trừ đi diện tích các mặt tiếp xúc và bằng:
320 + 130 – 140 = 310 (m2).
Chi phí để sơn khối bê tông như Hình 3 là:
310 . 25 = 7 750 (nghìn đồng) = 7 750 000 (đồng).
Vậy chi phí để sơn khối bê tông như Hình 3 là 7 750 000 đồng.
b) Thể tích của khối bê tông phía dưới là:
10 . 10 . 3 = 300 (m3).
Thể tích của khối bê tông phía trên là:
4 . 5 . 5 = 100 (m3).
Thể tích của khối bê tông là:
300 + 100 = 400 (m3).
Vậy thể tích của khối bê tông là 400 m3.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Để tính thể tích một hòn đá, bạn Na đã thực hiện như sau:
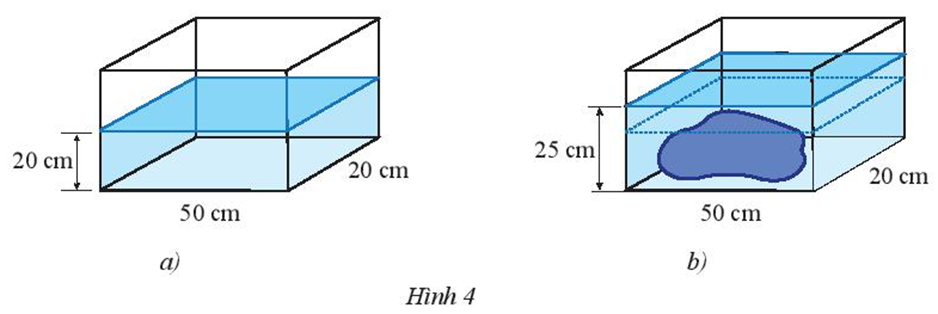
– Bạn ấy đổ nước vào cái bể kính hình hộp chữ nhật có hai cạnh đáy là 50 cm, 20 cm, mực nước đo được là 20 cm (Hình 4a).
– Sau đó bạn ấy đặt hòn đá vào bể thì thấy nước ngập hòn đá và mực nước đo được là 25 cm (Hình 4b).
Em hãy giúp bạn Na tính thể tích của hòn đá.
Câu hỏi:
Để tính thể tích một hòn đá, bạn Na đã thực hiện như sau:
– Bạn ấy đổ nước vào cái bể kính hình hộp chữ nhật có hai cạnh đáy là 50 cm, 20 cm, mực nước đo được là 20 cm (Hình 4a).
– Sau đó bạn ấy đặt hòn đá vào bể thì thấy nước ngập hòn đá và mực nước đo được là 25 cm (Hình 4b).
Em hãy giúp bạn Na tính thể tích của hòn đá.
Trả lời:
Thể tích nước ban đầu ở bể (Hình 4a) là:
50 . 20 . 20 = 20 000 (cm2).
Thể tích nước sau khi cho hòn đá vào bể (Hình 4b) là:
50 . 20 . 25 = 25 000 (cm2).
Thể tích hòn đá bằng thể tích nước dâng lên và bằng:
25 000 – 20 000 = 5 000 (cm2).
Vậy thể tích hòn đá là 5 000 cm2.====== **** mời các bạn xem câu tiếp bên dưới **** =====
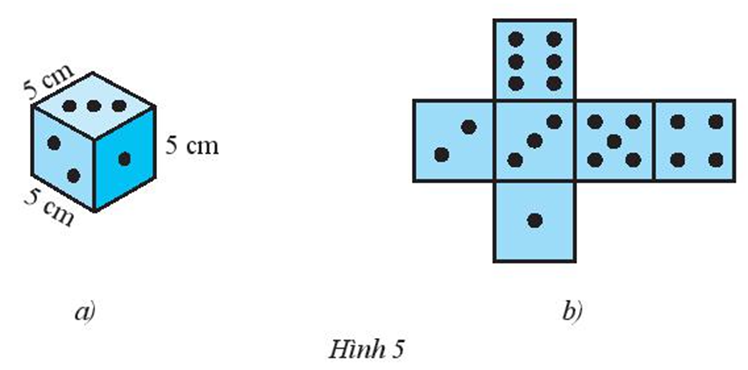
- Hùng làm một con xúc xắc hình lập phương có kích thước như Hình 5a từ tấm bìa có hình dạng như Hình 5b. Em hãy tính diện tích tấm bìa và thể tích con xúc xắc.
Câu hỏi:
Hùng làm một con xúc xắc hình lập phương có kích thước như Hình 5a từ tấm bìa có hình dạng như Hình 5b. Em hãy tính diện tích tấm bìa và thể tích con xúc xắc.
Trả lời:
Diện tích tấm bìa là diện tích các mặt của hình lập phương.
Diện tích các mặt của con xúc xắc hình lập phương là:
6 . 52 = 150 (cm2).
Thể tích con xúc xắc hình lập phương là:
52 = 125 (cm3).
Vậy diện tích tấm bìa là 150 cm2 và thể tích con xúc xắc là 125 cm3.====== **** mời các bạn xem câu tiếp bên dưới **** =====
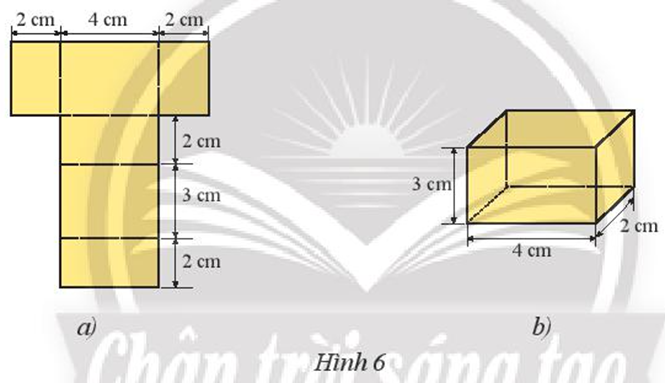
- Hãy vẽ và gấp tấm bìa như Hình 6a thành một hình hộp chữ nhật như Hình 6b. Tính tổng diện tích các mặt và thể tích của hình hộp.
Câu hỏi:
Hãy vẽ và gấp tấm bìa như Hình 6a thành một hình hộp chữ nhật như Hình 6b. Tính tổng diện tích các mặt và thể tích của hình hộp.
Trả lời:
Diện tích toàn phần của hình hộp chữ nhật bằng diện tích xung quanh cộng với diện tích 2 mặt đáy.
Stp = 2h(a + b) + 2ab.
(với a, b, h lần lượt là chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật).
Cắt tấm bìa theo các kích thước như Hình 6a. Sau đó gấp theo đường kẻ đậm ta được Hình 6b.
Tổng diện tích các mặt của hình hộp chữ nhật là:
2 . 3 . (4 + 2) + 2 . 4 . 2 = 52 (cm2).
Thể tích của hình hộp chữ nhật là:
4 . 2 . 3 = 24 (cm2).
Vậy tổng diện tích các mặt và thể tích của hình hộp chữ nhật lần lượt là 52 cm2 và 24 cm2.====== **** mời các bạn xem câu tiếp bên dưới **** =====