Câu hỏi:
Quan sát hình lăng trụ đứng tứ giác trong Hình 3.
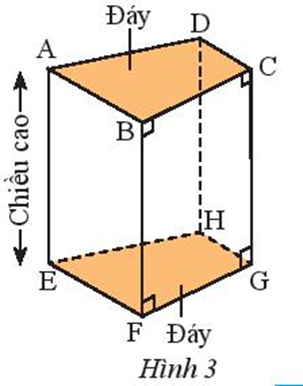
a) Hãy chỉ ra các mặt đáy và mặt bên của lăng trụ đứng tứ giác.
b) Cạnh bên AE bằng các cạnh nào?
Trả lời:
a) Hình lăng trụ đứng tứ giác ABCD.EFGH có:
– Các mặt đáy là: ABCD; EFGH.
– Các mặt bên là: ABFE; BCGF; CDHG; ADHE.
b) Hình lăng trụ đứng tứ giác ABCD.EFGH có các mặt bên là hình chữ nhật.
Khi đó:
+ ABFE là hình chữ nhật nên AE = BF.
+ BCGF là hình chữ nhật nên BF = CG.
+ CDHG là hình chữ nhật nên CG = DH.
+ ADHE là hình chữ nhật nên DH = AE.
Do đó AE = BF = CG = DH.
Vậy cạnh bên AE bằng các cạnh: BF; CG; DH.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Quan sát lăng kính, hộp đèn và hộp quà ở hình bên dưới. Cho biết các mặt bên của chúng ta là các hình gì.
Câu hỏi:
Quan sát lăng kính, hộp đèn và hộp quà ở hình bên dưới. Cho biết các mặt bên của chúng ta là các hình gì.

Trả lời:
Quan sát lăng kính, hộp đèn và hộp quà. Ta thấy các mặt bên của chúng là các hình chữ nhật.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
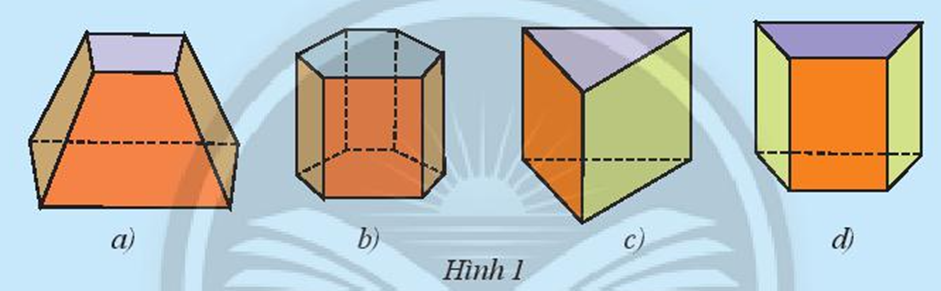
- Hình nào sau đây có:
a) các mặt bên là hình chữ nhật và hai mặt đáy là hình tam giác?
b) các mặt bên là hình chữ nhật và hai mặt đáy là hình tứ giác?
Câu hỏi:
Hình nào sau đây có:
a) các mặt bên là hình chữ nhật và hai mặt đáy là hình tam giác?
b) các mặt bên là hình chữ nhật và hai mặt đáy là hình tứ giác?
Trả lời:
Quan sát các hình, ta thấy:
– Hình 1a: các mặt bên là hình thang và hai mặt đáy cũng là hình thang.
– Hình 1b: các mặt bên là hình chữ nhật và hai mặt đáy là hình lục giác.
– Hình 1c: các mặt bên là hình chữ nhật và hai mặt đáy là hình tam giác.
– Hình 1d: các mặt bên là hình chữ nhật và hai mặt đáy là hình thang.
a) Hình 1c có các mặt bên là hình chữ nhật và hai mặt đáy là hình tam giác.
b) Hình 1d có các mặt bên là hình chữ nhật và hai mặt đáy là hình tứ giác (hình thang).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hộp kẹo sôcôla (Hình 4a) được vẽ lại như Hình 4b có dạng hình lăng trụ đứng. Hãy chỉ rõ mặt đáy, mặt bên, cạnh bên của hình lăng trụ đó.
Câu hỏi:
Hộp kẹo sôcôla (Hình 4a) được vẽ lại như Hình 4b có dạng hình lăng trụ đứng. Hãy chỉ rõ mặt đáy, mặt bên, cạnh bên của hình lăng trụ đó.

Trả lời:
Hộp kẹo sôcôla có dạng hình lăng trụ đứng như Hình 4b.
Hình lăng trụ đứng ABC.MNP có:
– Mặt đáy: ABC; MNP.
– Mặt bên: ABNM; BCPN; ACPM.
– Cạnh bên: AM; BN; CP.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tạo lập hình lăng trụ đứng tam giác có kích thước ba cạnh đáy là 2 cm, 3 cm, 4 cm và chiều cao 3,5 cm theo hướng dẫn sau:
– Vẽ ba hình chữ nhật với kích thước như Hình 5a.
– Cắt miếng bìa như hình vẽ rồi gấp theo đường nét đứt, ta được hình lăng trụ đứng tam giác như Hình 5b.
Câu hỏi:
Tạo lập hình lăng trụ đứng tam giác có kích thước ba cạnh đáy là 2 cm, 3 cm, 4 cm và chiều cao 3,5 cm theo hướng dẫn sau:
– Vẽ ba hình chữ nhật với kích thước như Hình 5a.
– Cắt miếng bìa như hình vẽ rồi gấp theo đường nét đứt, ta được hình lăng trụ đứng tam giác như Hình 5b.

Trả lời:
Cắt hình chữ nhật có kích thước như Hình 5a rồi gấp các cạnh theo đường nét đứt để được hình lăng trụ đứng tam giác như Hình 5b.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tạo lập hình lăng trụ đứng có đáy là hình vuông cạnh 3 cm và chiều cao 5 cm.
Câu hỏi:
Tạo lập hình lăng trụ đứng có đáy là hình vuông cạnh 3 cm và chiều cao 5 cm.
Trả lời:
Tạo lập hình lăng trụ đứng có đáy là hình vuông cạnh 3 cm và chiều cao 5 cm như sau:
– Vẽ bốn hình chữ nhật với kích thước như hình vẽ sau.
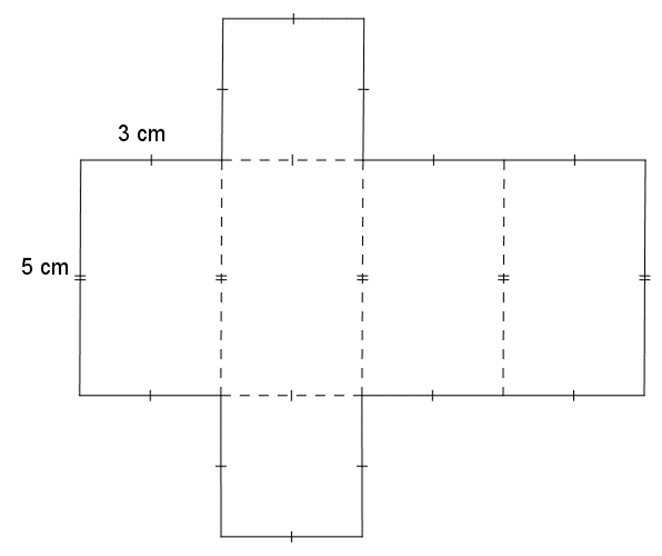
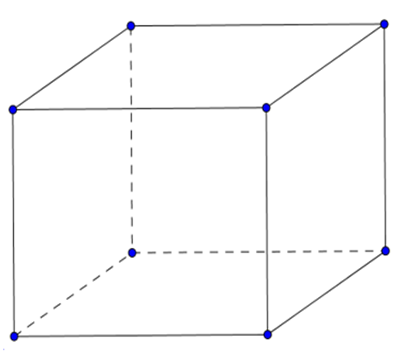
– Cắt miếng bìa như hình vẽ rồi gấp theo đường nét đứt, ta được hình lăng trụ đứng có đáy là hình vuông (như hình vẽ).
====== **** mời các bạn xem câu tiếp bên dưới **** =====